Introduction
Many different equivalent complete axiom systems for classical logic have been formulated. We want to show a few equivalent by using Prolog. We focus on Hilbert style propositional calculi that have the modus ponens inference rule and a set of axiom schemata.
We will show that the Frege, Łukasiewicz and Mendelson axiom schemata all produce the same consequences. We do so by representing the axiom systems in Prolog, and then let Prolog search for the equivalence.
Propositional Calculi
The axiom systems are depicted below. They all share the axiom schema A → ( B → A ) and the axiom schema ( A → ( B → C ) ) → ( ( A → B ) → ( A → C ) ). These two axiom schema make up minimal logic, which is not yet a classical logic since it is too weak.
To handle negation the different propositional calculi differ in their single additional axiom schema. In the Frege axiom system double negation elimination ¬ ¬ A → A is found, whereas the Łukasiewicz axiom system features a form of contraposition ( ¬ A → ¬ B ) → ( B → A ). Finally the Mendelson axiom system has reductio ad absurdum ( ¬ A → ¬ B ) → ( ( ¬ A → B ) → A ).
Prolog Representation
In the Prolog representation we use ¬ A := A → ⊥ so as to reduce the number of connectives to the implication only. We then represent the axiom schemata by facts for axiom/2. The Prolog logical variables turn it into schemata and we can use a further argument to name the axioms:
axiom(ax1, (A->_->A)).
axiom(ax2, ((A->B->C)->(A->B)->(A->C))).
axiom(dne, (((A->f)->f)->A)).
axiom(ctr, (((A->f)->B->f)->B->A)).
axiom(raa, (((A->f)->B->f)->((A->f)->B)->A)).
To form the axiom systems we need to find a way to record a set of axiom schemata. We do so by a further fact logic/2 which has an argument for the name of the axiom system. We can use multiple facts to list all the axiom schemata that belong to an axiom system:
logic(fre, ax1).
logic(fre, ax2).
logic(fre, dne).
logic(luk, ax1).
logic(luk, ax2).
logic(luk, ctr).
logic(men, ax1).
logic(men, ax2).
logic(men, raa).
Prolog Search
To search for a Hilbert style proof we have to try the modus ponens inference rule. To avoid an infinite loop we use iterative deepening. The prove/5 predicate therefore has an integer parameter N that does count down on the number of modus ponens applications:
prove(B, K, N, M, mp(B,P,Q)) :-
N > 0,
H is N-1,
prove((A->B), K, H, J, P),
prove(A, K, J, M, Q).
We need to also try the axiom schemata of the given axiom system. The prove/5 predicate therefore has a further parameter K with the name of the axiom system. Searching the axiom system is a matter of first calling logic/2 and then axiom/2 that do represent our axiom systems.
prove(B, K, N, N, ax(I,B)) :-
logic(K, I),
axiom(I, T),
unify_with_occurs_check(B, T).
The unify_with_occurs_check/2 call is needed so that the Prolog system does not return cyclic terms. A proof that contains a cyclic term wouldn't be a valid proof since propositional formulas are finite. The predicate unify_with_occurs_check/2 is part of the ISO core Prolog standard.
Results
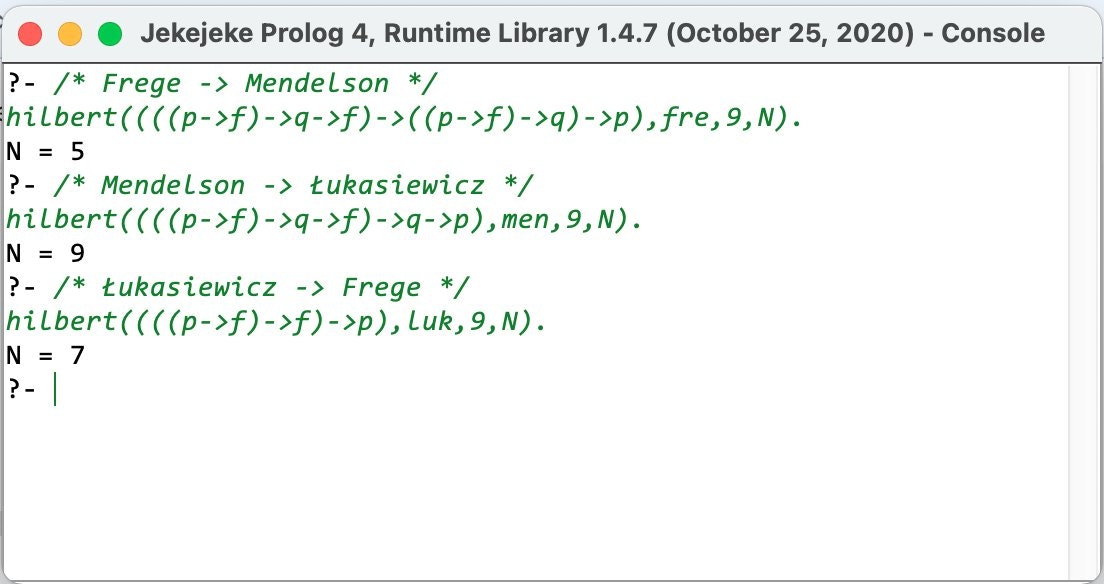
Lets denote the consequences in the Hilbert style propositional calculus from the axiom system L by Con(L). We can use the predicate prove/5 to check whether the axiom schemata R of one axiom system are reachable by another axiom system L, by checking R ⊆ Con(L). Here are some results, the minimal number of needed modus ponens applications is returned:
Because R ⊆ Con(L) implies Con(R) ⊆ Con(L) we can therefore conclude that Can(Mendelson) ⊆ Con(Frege), Con(Łukasiewicz) ⊆ Con(Mendelson) and Con(Frege) ⊆ Con(Łukasiewicz). The last two together give Con(Frege) ⊆ Con(Mendelson). Together with the first one we get Con(Frege) = Con(Mendelson). Etc..
Open Source: Find a Hilbert proof in variety of propositional logics
https://gist.github.com/jburse/51cd3886c7ceef5035ea7e2860b096a2#file-admissible-pl
Full Proofs: Logical equivalence of different axiom systems
https://gist.github.com/jburse/51cd3886c7ceef5035ea7e2860b096a2#gistcomment-3542691