Dogelog Player is a Prolog system written 100% in Prolog itself. It got recently extended by a library(util/hash) that provides a hash table map. It is an imperative datastructure that uses change_arg/3 for destructive updates.
A further library(util/tree) was realized, that uses the rules of Okasaki's Red-Black tree with destructive updates. Applied to the million rows challenge, performance differs not much from a hash table and it gives us sorted key results.
Okasaki's Red-Black Tree
Okasaki's Red-Black tree can be taken from the 1999 paper Red-Black Trees in a Functional Setting by Chris Okasaki. It features some Haskel code that presents a red-black tree insertion as a binary tree insertion followed by a rebalancing:
insert :: (Ord a) => a -> Tree a -> Tree a
insert x s = makeBlack $ ins s
where ins E = T R E x E
ins (T color a y b)
| x < y = balance color (ins a) y b
| x == y = T color a y b
| x > y = balance color a y (ins b)
makeBlack (T _ a y b) = T B a y b
The algorithm is based on node coloring, new nodes are colored red and the root is colored black. During the unwinding the function balance handles 4 different cases. Each case handles a situation where two red nodes follow each other along a tree branch:
balance :: Color -> Tree a -> a -> Tree a -> Tree a
balance B (T R (T R a x b) y c) z d = T R (T B a x b) y (T B c z d)
balance B (T R a x (T R b y c)) z d = T R (T B a x b) y (T B c z d)
balance B a x (T R (T R b y c) z d) = T R (T B a x b) y (T B c z d)
balance B a x (T R b y (T R c z d)) = T R (T B a x b) y (T B c z d)
balance color a x b = T color a x b
SWI-Prolog features a library(rbtrees) with a functional tree implementation. Source code inspection reveals that it most likely implements something else, there are two routines fix_left and fix_right, whereas Okasaki has only one routine balance.
Prolog Non-Backtracking Realisation
We set forth to implement the Okasaki's Red-Black tree in Dogelog Player. To represent the binary tree we use the atom '$NIL' for the empty node and the compound '$NOD'(Color, Left, Pair, Right) for a colored binary node. Insert reads straight forward:
sys_tree_set(T, K, V) :- T = '$NOD'(_, L, K2-_, _), K @< K2, !,
(L = '$NIL' ->
sys_node_make('$RED', K, V, L2),
change_arg(2, T, L2);
sys_tree_set(L, K, V),
sys_node_balance(T)).
sys_tree_set(T, K, V) :- T = '$NOD'(_, _, K2-_, _), K == K2, !,
arg(3, T, P),
change_arg(2, P, V).
sys_tree_set(T, K, V) :- T = '$NOD'(_, _, _, R),
(R = '$NIL' ->
sys_node_make('$RED', K, V, R2),
change_arg(4, T, R2);
sys_tree_set(R, K, V),
sys_node_balance(T)).
The code features the use of change_arg/3. It has become our favorite gadget to realize imperative datastructures in Prolog. We do not need a foreign function interface and/or realize a variety of low level helpers that deal with updateable state.
sys_node_balance(T) :- T = '$NOD'('$BLK', P, U, Q),
(P = '$NOD'('$RED', M, V, N),
(M = '$NOD'('$RED', _, _, _), !,
change_arg(1, M, '$BLK'),
change_arg(1, P, '$BLK'),
change_arg(2, P, N),
change_arg(3, P, U),
change_arg(4, P, Q),
change_arg(1, T, '$RED'),
change_arg(2, T, M),
change_arg(3, T, V),
change_arg(4, T, P);
Etc..
Subsequently one will not find setup_call_cleanup/3 brakets in the source code. Instead we can rely on its Prolog garbage collector integration. The above shows the Prolog code of the first rule of Okasaki's balance again implemented with change_arg/3.
We run a couple of tests and compared it to SWI-Prolog red-black trees in terms of worst case tree depth. It seems SWI-Prolog has shorter trees! For example depth 6 is found up to 26 elements, whereas Okasaki already gives up after 21 elements.
Million Rows with Hash Table
Recently the Billion Row Challenge (1BRC) made it rounds on the internet. Originally cast as a programming exercise for Java, we solve the problem with Prolog. We use a smaller dataset of of rows that are directly synthesized through backtracking.
sample(W, X) :-
station(W, MU, SIG),
gauss(Y),
X is SIG*Y+MU.
The samples are generated from a gaussian distribution. We can use library(aggregate) to compute the 1st and 2nd moments of the sample data. And from this recompute the mean and the standard deviation of the sample data as seen in predicate test/4:
test(K, W, MU, SIG) :-
aggregate((count, sum(X), sum(Y)), N^(between(1,K,N), sample(W,X),
Y is X**2), (C,S,R)), MU is S/C, SIG is sqrt(R/C-MU**2).
With a hash table we can compute the aggregate functions via change_arg/3 by means of destructive updates. This makes the materialization of samples superflous. Also the size is small, we need only room for the distinct keys.
% ?- test(1000, W, MU, SIG).
W = 'São Paulo (Mirante de Santana)', MU = 19.175261600480184, SIG = 2.9419003330546714;
W = 'Miami International Airport', MU = 25.191758853272347, SIG = 2.5431587391597796;
W = 'Moscow (VVC)', MU = 5.557102296814446, SIG = 5.9460935875871685;
W = 'Reykjavík', MU = 5.637930873810601, SIG = 2.980821055130151;
W = 'Tokyo (Tokyo Midtown)', MU = 16.205279745398563, SIG = 3.994482163663803;
W = 'Anchorage (Ted Stevens Airport)', MU = 2.950478640540103, SIG = 5.146844924993232;
W = 'New Delhi (Safdarjung)', MU = 25.186210879738443, SIG = 5.598469601538567;
W = 'Sydney Observatory Hill', MU = 18.346643952102017, SIG = 4.532349819457653;
W = 'Cape Town (Cape Town International)', MU = 16.929881442318475, SIG = 3.47349624404747;
W = 'Cairo Airport', MU = 21.218232888758244, SIG = 3.865451138742402.
other Prolog systems can master the challenge only by consuming more memory than 1 GB. Where as the hash table approach uses less than 1 MB memory and doesn’t change with the number of samples. But the resulting key ordering is rather random.
Million Rows with Red-Black Tree
The keys could be sorted via the ISO core sort/1 call. As an alternative we implemented the aggregate function with our new red-black trees. We should then see the resulting key ordered as well, by the Prolog lexical ordering of the (@<)/2 predicate:
?- test(1000, W, MU, SIG).
W = 'Anchorage (Ted Stevens Airport)', MU = 3.1110190621107643, SIG = 5.036556630299001;
W = 'Cairo Airport', MU = 21.32393938484394, SIG = 3.871258304849876;
W = 'Cape Town (Cape Town International)', MU = 17.01045315282821, SIG = 3.571428581626268;
W = 'Miami International Airport', MU = 25.262843165034674, SIG = 2.4547543736580284;
W = 'Moscow (VVC)', MU = 5.803592162802512, SIG = 5.8711209925691366;
W = 'New Delhi (Safdarjung)', MU = 24.97163462987483, SIG = 5.4169600341267685;
W = 'Reykjavík', MU = 5.578282662724365, SIG = 2.9452193896409935;
W = 'Sydney Observatory Hill', MU = 18.23621351823158, SIG = 4.461956557748384;
W = 'São Paulo (Mirante de Santana)', MU = 19.06076863750828, SIG = 2.966251082116513;
W = 'Tokyo (Tokyo Midtown)', MU = 16.25213836693857, SIG = 4.089507684566505.
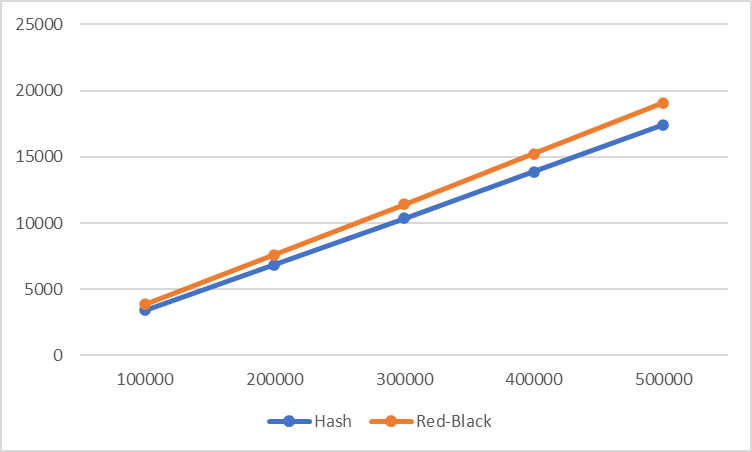
We compare hash table versus red black tree. Since we have very few key and a lot of samples, we will only measure the lookup and less the insert. If we would run different key set sizes we would possibly see O(1) versus O(log N). We see only a constant factor of our implementation overhead, which is luckily below 10%:
Conclusions
change_arg/3 has become our favorite gadget to realize imperative datastructures in Prolog. No setup_call_cleanup/3 brakets are needed, since we can rely on its Prolog garbage collector integration. We compared hash table versus red black tree. For the million row challenge we see an overhead below 10%.
Million Rows Challenge in Dogelog Player
https://medium.com/@janburse_2989/million-rows-challenge-in-dogelog-player-8f4fdb217189
User Manual: library(util/tree)
https://www.novacuor.ch/doctab/doclet/docs/12_lang/07_libraries/02_util/06_tree.html