2022 年 12 月に Yan 等が発表した SQIF という量子素因数分解アルゴリズムを解説しています. 今回は Part 3 として, SQIF のベースとなっている Schnorr の素因数分解法の処理内容を紹介します.
Part 1: 論文の概要
Part 2: 平方差法による素因数分解
Part 3: Schnorr の素因数分解法 (本記事)
Part 4: SQIF の詳細
Part 5: SQIF の数値実験の分析
Part 6: まとめ
変更履歴
- 2023年5月29日:一連の記事へのリンクを追加しました。また各記事の用語やトーンを揃えるため、全体的に加筆変更しました。
格子と格子問題
Schnorr の素因数分解法は, 素因数分解を格子問題と呼ばれる別の数学問題に変換させることを特徴にしています. そこでまずはじめに格子問題についてまとめます.
格子
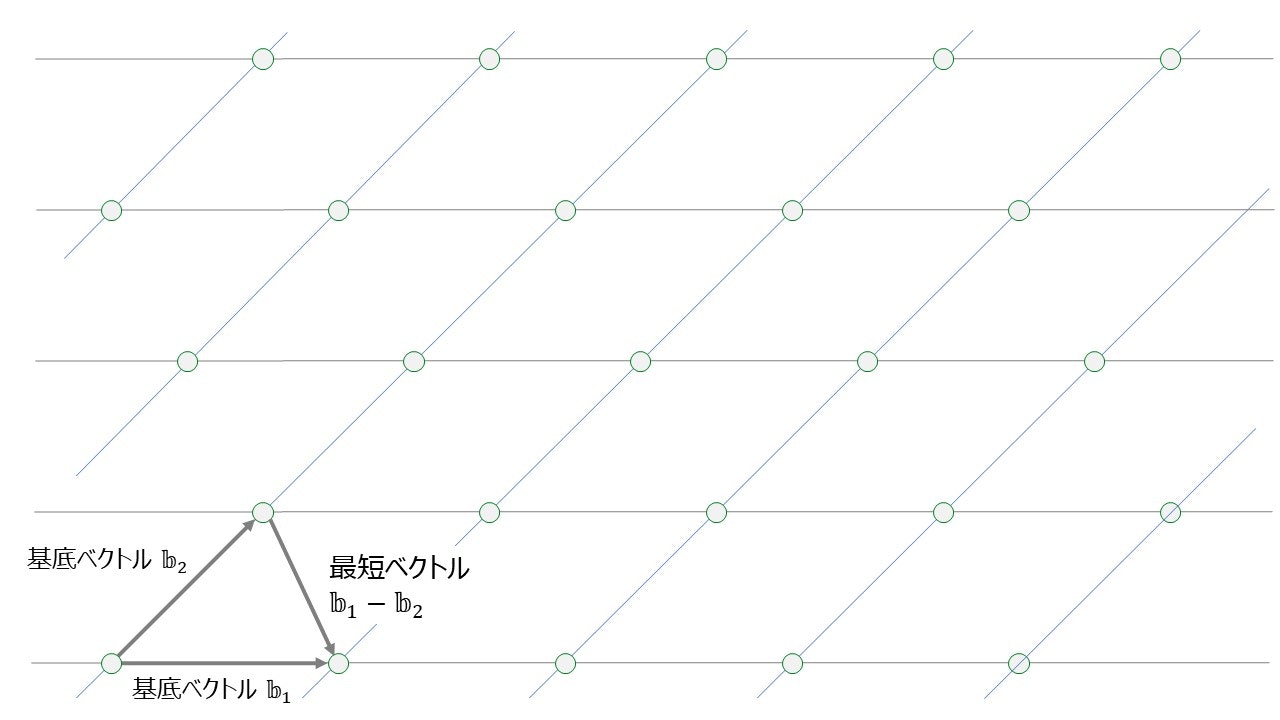
$n$ 個の一次独立なベクトルの整数係数の線型和全体の集合を格子 (lattice), これらベクトルを格子の基底ベクトル (basis) と呼びます. 例えば2次元空間における基底ベクトル $\mathbb{b}_1,\mathbb{b}_2$ から生成される格子は下図の○で表される点の集合となります.
最短ベクトル問題
与えられた格子から, 長さが最短となるベクトルを求める問題を最短ベクトル問題 (SVP: Shortest Vector Problem) と呼びます. さきほどの例の格子では, 下図のようにベクトル $\mathbb{b}_1-\mathbb{b}_2$ が最短ベクトルになっています. このように格子の次元が低次の場合には最短ベクトルは容易に求められますが, 高次の場合, SVP は解くのが難しい問題であることが知られています.
最近ベクトル問題
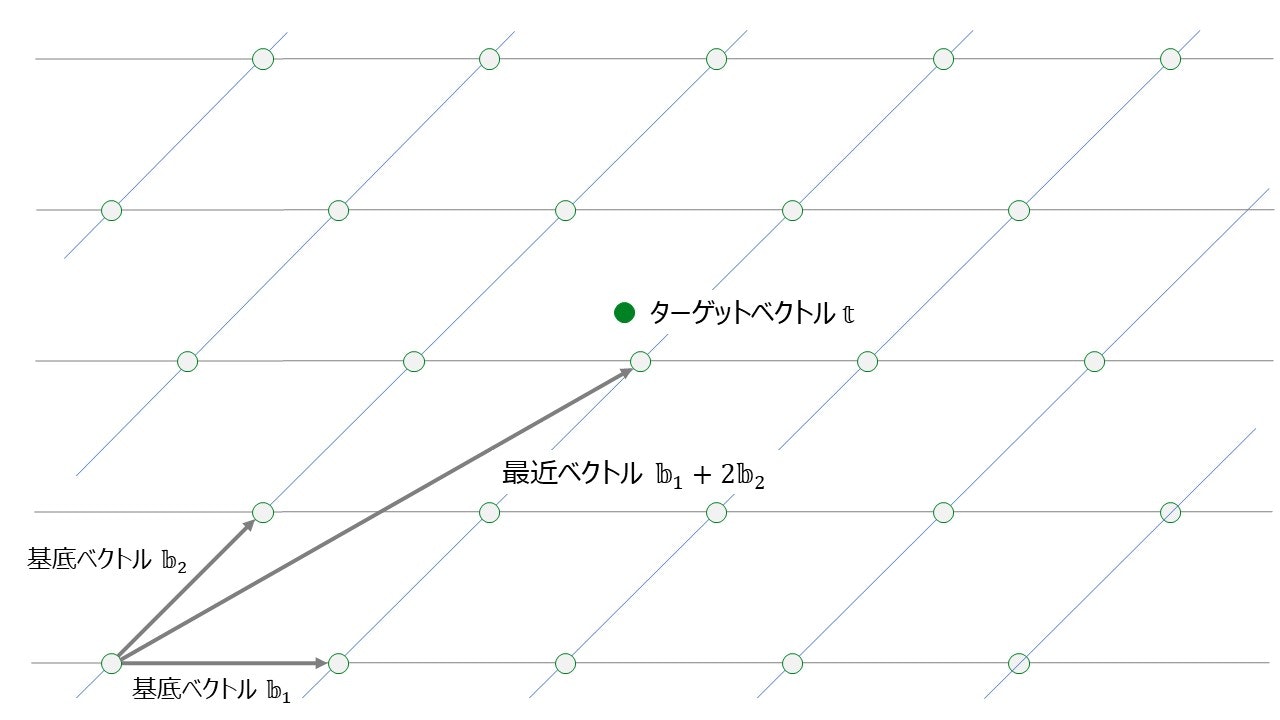
与えられた格子とターゲットベクトルと呼ばれるベクトルから, ターゲットベクトルに最も近い格子内のベクトルを求める問題を最近ベクトル問題 (CVP: Closest Vector Problem) と呼びます. ターゲットベクトルは格子ベクトルとは限りません (逆にターゲットベクトルが格子ベクトルの場合には CVP は簡単に解けるので, 一般にはターゲットベクトルが格子ベクトルでない場合を考えることになります). さきほどの例の格子においては, 下図のターゲットベクトルに対する最近ベクトルは $\mathbb{b}_1+2\mathbb{b}_2$ です. このように格子の次元が低次の場合には最近ベクトルは容易に求められますが, 高次の場合には CVP は解くのが難しい問題であることが知られています.
LLL アルゴリズム
LLL アルゴリズム (Lenstra-Lenstra-Lovasz アルゴリズム) は与えられた格子の基底ベクトルを「良い」基底ベクトルに変換するアルゴリズムですが, 同時に SVP を解くアルゴリズムとしても知られています. この記事では「良い」基底ベクトルの意味や LLL アルゴリズムの具体的な処理手順は紹介しませんが, LLL アルゴリズムは格子次元に対する多項式時間アルゴリズムになるため, とても優れたアルゴリズムになっています. 反面, 得られる SVP の解は近似解であり, 近似率は(理論的には)格子次元に関する指数関数になることも知られています. ただし経験的には LLL アルゴリズムが求める解の近似率はそこまで悪くないことが多いため, SVP を解く上で LLL アルゴリズムは広く利用されています.
Babai アルゴリズム
Babai アルゴリズムは CVP を近似的に解くアルゴリズムです. 特に, 与えられた基底ベクトルに LLL アルゴリズムを適用してから Babai アルゴリズムを併用した場合, 格子次元に関する多項式時間アルゴリズムになることが知られていますが, 近似率は格子次元に関する指数関数となります. Babai アルゴリズムの具体的な処理手順は別の文献を参照ください.
Schnorr の素因数分解法
それでは Schnorr による素因数分解法の処理内容を説明します.
アイディア
Schnorr の素因数分解法の目標は平方差法における拡張関係式を収集することです. これを実現するために Schnorr の素因数分解法は以下のような基底ベクトルから生成される格子を考えます. ここで $*$ で表された成分は後で定めます:
\mathbb{b}_1 = \begin{pmatrix} * \\ * \\ \log{p_1} \end{pmatrix},~
\mathbb{b}_2 = \begin{pmatrix} * \\ * \\ \log{p_2} \end{pmatrix},~
\dots,
\mathbb{b}_s = \begin{pmatrix} * \\ * \\ \log{p_s} \end{pmatrix}.
このとき
\mathbb{t} = \begin{pmatrix} * \\ * \\ \log{N} \end{pmatrix}
をターゲットベクトルとする CVP を考えることで
\mathbb{t} \approx
e_1 \mathbb{b}_1 + e_2 \mathbb{b}_2 + \dots + e_s \mathbb{b}_s
を満たす整数 $e_1,\dots,e_s$ を得ることができます. 特に最終行に着目することで $\log{N}$ $\approx$ $e_1 \log{p_1}$ $+$ $e_2 \log{p_2}$ $+$ $\dots$ $+$ $e_t$ $\log{p_s}$, つまり $N$ $\approx$ $p_1^{e_1}$ $\times$ $\dots$ $\times$ $p_s^{e_s}$ という関係式が得られます. 係数 $e_i$ は負になる可能性があるため, 正の項と負の項を別々にして $u=\prod_{e_i>0} p_i^{e_i}$, $v=\prod_{e_i<0} p_i^{-e_i}$ と定めることにすれば, $N$ $\approx$ $p_1^{e_1}$ $\times$ $p_2^{e_2}$ $\times$ $\dots$ $\times$ $p_t^{e_s}$ $=$ $\frac{u}{v}$ つまり $u \approx vN$ となります. よって $u-vN$ の絶対値は小さく, べき積 $\pm q_1^{f_1} \times \dots q_t^{f_t}$ と素因数分解できることが期待できます. 特に CVP の近似解の近似率が良いほど $u-vN$ の絶対値は小さくなり, 小さな素数のべき積になる可能性が高くなります. 他方で $u \equiv u-vN \pmod{N}$ が成立することから, 拡張関係式 $\prod_{e_i>0} p_i^{e_i} \equiv \pm q_1^{f_1} \times \dots q_t^{f_t} \pmod{N}$ が得られます. なお平方差法ではたくさんの拡張関係式が必要となるので, 基底ベクトルの $*$ で表される成分にランダムな要素を入れることで, 基底ベクトルのバリエーションを持たせます.
Schnorr の素因数分解法の具体的な処理は以下のようになります. 以下では Yan 等の論文に記された方法を使用しますが, 詳細はオリジナル論文を参照ください.
(1) 格子の生成
(2) 拡張関係式の収集 (CVP の求解)
(3) 行列計算
(4) $N$ の因数分解
格子の生成
素因数分解したい合成数 $N$ と適当な方法で定義された素数の集合
P=\{ p_1, \dots, p_s \}
に対し, 以下の基底ベクトルから生成される格子を定める:
\mathbb{b}_1 = \begin{pmatrix} f(1) \\ 0 \\ \vdots \\ 0 \\ N^c \log{p_1} \end{pmatrix},~
\mathbb{b}_2 = \begin{pmatrix} 0 \\ f(2) \\ \vdots \\ 0 \\ N^c \log{p_2} \end{pmatrix},~
\dots,
\mathbb{b}_s = \begin{pmatrix} 0 \\ 0 \\ \vdots \\ f(s) \\ N^c \log{p_s} \end{pmatrix}.
ここで関数 $f$ は ${1,2,\dots,s}$ 上のランダムな置換である. また $c$ は CVP を適切に解けるようにするためのウェイトを意味する定数であり, 具体的な値は別途定められる.
(2) 拡張関係式の収集 (CVP の求解)
(1) で定義された格子において, ターゲットベクトル
\mathbb{t} = \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ N^c \log{N} \end{pmatrix}
に対する CVP を解く. 具体的には
(2-1) 基底ベクトルに対して LLL アルゴリズムを適用
(2-2) (2-1) で得られた基底ベクトルに対して Babai アルゴリズムを適用
(2-3) (2-2) で得られた CVP の近似解に対して ENUM と呼ばれるアルゴリズムを適用し, 近似精度のより良い解を求める (ENUM の詳細は Schnorr のオリジナル論文を参照ください).
(2-4) (2-3) で得られた近似解 $\mathbb{t} \approx e_1 \mathbb{b}1 + \dots + e_s\ \mathbb{b}s$ に対して $u = \prod{e_i>0} p_i^{e_i}$, $v = \prod{e_i<0} p_i^{-e_i}$ と定め, さらに $u-vN$ の素因数分解 $\pm q_1^{f_1} \times \dots \times q_t^{f_t}$ を求める. このとき拡張関係式
\prod_{e_i>0} p_i^{e_i} \equiv \pm q_1^{f_1} \times \dots \times q_t^{f_t} \pmod{N}
が得られる.
(3) 行列の計算
得られた拡張関係式から生成されるベクトルを行ベクトルとする行列を生成し, 掃き出し法を適用する.
(4) 素因数分解
(3) で得られた関係式から $N$ の因数を得る.
Schnorr の素因数分解法の課題
Schnorr の素因数分解法は格子の最近ベクトル問題を解くことで素因数分解を実現しているのですが, 格子の次元が大きくなるにつれて近似解の精度が低下するため, 必要な個数の拡張関係式を収集するための計算時間が不明であるという指摘を受けています. 実際, Ducas の解析 によると, Schnorr 法が既存の(二次篩法などの)素因数分解アルゴリズムよりも効率を良くするには高次元の格子が必要であるが, 高次元の格子では精度の良い近似解を求めるのが難しくなることが指摘されています.
まとめ
本記事では Schnorr の素因数分解法を紹介しました. Schnorr 法は素因数分解問題を最近ベクトル問題に変換し, 最近ベクトル問題の近似解から拡張関係式を求めます. しかし Babai アルゴリズムなどの既存の最近ベクトル問題の求解法は格子次元が大きくなるにつれて近似精度が悪くなると言う課題があります. そこで SQIF は CVP の求解をさらに最適化問題に変換することで, 近似精度を保とうとしています. 次回は SQIF の詳細な処理手順を紹介します.