第20話 ゲルフォントの定数

この記事は仮面ライダービルドの数式の第20話です。

e^π-π≈20

この式はおおよそ20、という式です。厳密に計算するとこんな感じです。

e^π-π=19.9990999792…

Wikipediaに”ほとんど整数”という項目があります。
一見整数に見えないのに、計算してみると整数に近い、という式が載っています。

e^πはゲルフォントの定数と呼ばれます。
オイラーの式を変形することで、-1^(-i)という数になります。

e^{iπ}=-1

両辺を-i乗します。

e^{i\pi \cdot -i}=e^π=(-1)^{-i}

今回の式は、特にほとんど整数になる理由が見つかって無いようで、偶然という見解のようです。
ただ、$e^{\pi\sqrt{1}}$と考えると、偶然とはいえ、出来すぎているかもしれません…。
(この式は第43話で説明します。)

ところで、e$^π$は、$π^e$と近い数で、1未満しか離れていません。
どっちが大きいかわかりますか？

e$^π$と$π^e$はどちらが大きいかの解説

グーグル先生に聞けば一発です。

e^\pi=23.1406926\cdots\\
\pi^e=22.4591577\cdots

ということなので、大きいのは、$e^π$なのですが、計算機無しで計算するのは難しいでしょう。
そこで、式を次のように変形します。

e^{\pi}=e^{e\cdot\frac{1}{e}\cdot\pi} = e^{\frac{1}{e}\cdot e\pi}\\
\pi^{e}=\pi^{\pi\cdot\frac{1}{\pi}\cdot e} = \pi^{\frac{1}{\pi}\cdot e\pi}\\

つまり、$e^{1/e}$ と $π^{1/π}$、どっちが大きいか、という問題に変換できます。
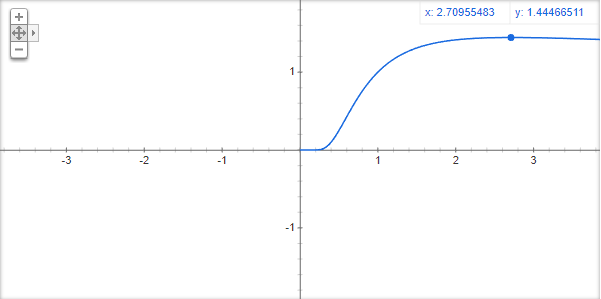
そして、次の関数のグラフを考えてみます。

f(x)= x^{\frac{1}{x}}

これの極大値、極小値を求めたいのですが、この関数を微分するのはかなり辛いです。
そこで、次の公式を使い、別の関数を調べてみましょう。

a<b ならば、\log{a}<\log{b}\\

g(x)=\log{x^{\frac{1}{x}}}=\frac{1}{x}\log{x}

これを微分するのは、先程の関数よりかなり楽です。

g'(x)=(-\frac{1}{x^2})\log{x}+\frac{1}{x}(\frac{1}{x})=\frac{1-\log{x}}{x^2}

では、g'(x)=0を計算しましょう。
ちなみに、x>0 とします。

\begin{align}
\frac{1-\log{x}}{x^2}=0\\
1-\log{x}=0\\
\log{x}=1\\
x=e
\end{align}

あとは、表にまとめます。

x	0	...	e	...
g'(x)		正	0	負
f(x)		／	e^(1/e)	＼

つまり、eのときに極大値を取ります。
ということは、以下のことがわかります。

e^\pi>\pi^e

ちなみに、グラフはこんな感じになります。
わかりにくいですが、eを極大値としてほんの少しずつ下がっていきます。