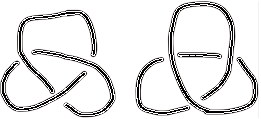この記事は仮面ライダービルドの数式の第35話です。
\#\{nontrivaial\ knot|C(L)≤8\}=35
8つ以下の交点をもつ結び目は35通りあります。
例えば上の図の輪は3箇所の交差があるので交点3の輪です。
しかし、右の輪は交点0の輪と同じ形とみなします。
左は紐が絡み合ってもし引っ張ったとしたなら結び目になってしまうでしょう。
しかし右は普通の輪に戻ってしまいます。
このように、交点8以下だと普通の輪に戻らない形が35通りあります。
表にするとこんな感じで、最小は3になります。
やはりというか、交点数が増えると種類数は爆発的に増えていきます。
| 交点数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 個数 | 1 | 0 | 0 | 1 | 1 | 2 | 3 | 7 | 21 | 49 | 165 |
この結び目理論は、DNAやタンパク質の解析なんかに使われていますし、
ここから発展して電子基板の配置をどうすれば立体交差が最小化できるか、
というのにも繋がっていきます。