はじめに
この記事は東京大学VRサークルUT-virtualのAdventCalendar2018の13日目の記事です。
東大志望の受験生だった僕が出会った美しい京大数学の過去問を紹介しつつ、その問題で扱われた性質を用いて、プログラミングの練習として、素数判定プログラムを作ったときの事をまとめてみました。
1995年 京都大学 後期 文系 第四問
早速ですが、こちらがその問題です。注目して欲しいのは(2)。「好きな自然数nを決めてよい。そのときのg(n)をあなたの得点とする」と、自分の得点を自分で決められるという、入試問題としては異彩を放つ面白い問題ですよね。
しかし、実際に解き始めてみるとこの問題のさらなる面白さに気付くことにるのです。(数学に自身のある皆さんは是非この先を読む前に挑戦してみてください)
とりあえずn=1としてg(n)を求めてみます。
この g(n)というのは(1n+2n+3n+4n+5n+6n)を7で割った余りを3倍したものになります。
n=1のときには(1+2+3+4+5+6)= 21 なので7で割ると…余りは0。
つまり g(n)=0 残念ながら1点ももらえません。
じゃあn=2で… (12+22+32+42+52+62)= 91
7で割ると…余りは0。ダメ。
n=3だと(13+23+33+43+53+63)= 441。7で割ると…余りは0。
まさか…!?
n=4だと(14+24+34+44+5+64)= 2275。7で割ると…余りは0。
n=5だと(15+25+35+45+55+65)= 12201。7で割ると…余りは0。
この問題、部分点狙いで適当な数を入れても答えが必ず0になってしまいます。
そして、
n=6だと(16+26+36+46+56+66)= 67171。7で割ると…余りは6。
つまりこの問題は6が好きな人だけが満点の18点を取ることができ、そうでない人は0点になるという、とんでもない問題なのです。
※正確にはnが(7の倍数-1)の時のみ g(n)=18となります。
※正確にはnが6の倍数の時のみ g(n)=18となります。
(※追記:コメントを頂き修正しました。詳しくはページの最後に。以下仮説の項でも同様のミスをしておりますが修正していません。)
仮説
nが(7の倍数-1)の時のみ(1n+2n+3n+4n+5n+6n)の余りが6となり、それ以外のnでは0になる。なかなか不思議な性質ではありませんか?
受験勉強で数学的な勘が鋭くなっていた僕は「この美しい性質が“7”だけの持つ性質であるはずがない。他の数でも同じことができるはずだ!」と思ったのです。そして、7が素数であることからこんな仮説を立てました。
素数pに対して、(1n+2n+3n+・・・+ (p-1)n)をpで割った余りは、nが(pの倍数-1)の時以外は0になり、nが(pの倍数-1)の時には(p-1)となる。
そして、この仮説が正しいことを確かめ、あわよくば素数判定機を作ろうと思い、スクリプトを書き始めました。(受験勉強しろ)
検証
当時の僕はプログラミングに興味を持ち始めたもののまだ授業で習ったExcelでのVBA程度しか使ったことがなく、しかも自分のPCにOfficeのソフトが入っていないという貧弱環境を生きていたため、無料でVBA的なことができるらしいと、GoogleSpreadSheetとGoogleAppsScriptで検証してみることにしました。
そのときの検証用のコードがこちらです↓↓↓(わかりやすくするために変数名とコメントは編集しました)
var p = 7; //京大の問題でいう7。ここを色々変えて検証する
var remainders = []; //remainders[i]にはiのn乗をpで割った余りが入る
var n = 1;
var sum = 0;
var g = [];
var i = 1;
//remaindersを(p-1)項まで初期化
for (i = 1;i <= p-1;i++){
remainders[i] = 1;
}
//好きな数nを1から(p-1)まで変えて試行
for(n = 1;n <= p-1;n++){
//1のn乗から(p-1)のn乗までをそれぞれpで割った余りを計算し、合計する
for (i = 1;i <= p-1;i++){
remainders[i] = (remainders[i]*i)%p;
sum = sum + remainders[i];
}
//和をpで割った余りを求める(n=p-1の時のみこの値がp-1になり、他では0になるはず)
g[n] = sum%p;
}
//仮説が正しければ、pが素数の時「0,0,...,0,p-1」となるはず
Browser.msgBox(g);
計算の簡略化のために、前章で説明した解き方とは少し違いますが、やってることは同じです。
数pに対して、(1n+2n+3n+・・・+ (p-1)n)をpで割った余り(過去問で言うg(n)の3倍してないver)がg[n]に代入され、n=1から順に出力されます。
さて、p=7の時、出力されたg[n]は 0,0,0,0,0,6。これは京大の過去問と一致します。
pを適当な素数に変えて試してみましょう…
p=5 ... 0,0,0,4
p=11 ... 0,0,0,0,0,0,0,0,0,10
p=29 ... 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,28
これは!どうやら仮説は正しそうです!!
(※追記: p=2の時はnの値に関わらずあまりが1となる為、「pが素数の時」ではなく「pが3以上の素数(奇素数)の時」が正しいです。また、奇素数の時に仮説の条件を満たすことは、巡回群の性質やフェルマーの小定理から示せるようです。コメントありがとうございました。)
試しにpに素数以外を入れてみると…
p=9 ... 0,6,0,6,0,6,0,6
p=12 ... 6,2,0,2,0,2,0,2,0,2,0
p=33 ... 0,22,0,22,0,22,0,22,0,19,0,22,0,22,0,22,0,22,0,19,0,22,0,22,0,22,0,22,0,19,0,22
奇数や半素数(2つの素数の積)で試しても、0,0,0,...にはなりません。
素数判定機、作れる気がしてきました…!
素数判定機
var sheet = SpreadsheetApp.getActiveSpreadsheet().getActiveSheet(); //シート取得
var p = sheet.getRange(7,3).getValue(); //シートからpを持ってくる
var remainders = [];
var n = 1;
var sum = 0;
var g = [];
var i = 1;
var limit = 2000; //pの上限を設定
var judge = 0; //素数判定用の数値追加
//pがlimit以下の自然数ならスタート
if(p >= 1 && p <= limit){
for (i = 1;i <= p-1;i++){
remainders[i] = 1;
}
for(n = 1;n <= p-1;n++){
for (i = 1;i <= p-1;i++){
remainders[i] = (remainders[i]*i)%p;
sum = sum + remainders[i];
}
g[n] = sum%p;
judge = judge + g[n]; //最終的にg[1]からg[p-1]までを足しあげた数がjudgeに代入されます
}
//素数かどうか判定
//judgeとg[p-1]がともにp-1と等しい(つまりg[]=[0,0,...,p-1])時のみtrue
if(judge == p-1 && g[p-1] == p-1){
sheet.getRange(11,6).setValue("素数");
}else{
sheet.getRange(11,6).setValue("素数じゃない");
}
}else{ //pがlimit以上だったときの処理
Browser.msgBox(limit + "までの自然数を入力してください");
}
コメント部分がコード変更点です。
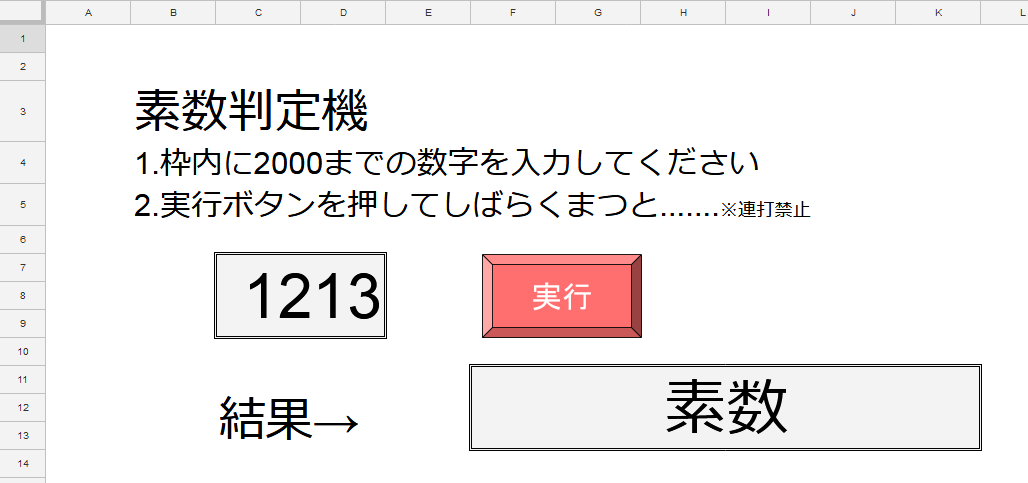
本日12/13ということで1213を判定してみると…ちゃんと素数と判定されました。
実用性
上の素数判定機の画像、2000までだとか連打禁止だとか、注意書きがうるさいですよね。実はこの判定機、処理がだいぶ重いため、大きな数を入れたりボタン連打するとフリーズします。
計算量のオーダーをみてみると…なんと p2。
pが大きくなると、1からp-1までの全てで割り算するよりもはるかに遅いという始末。残念ながら実用性はありません。ちなみに1213を判定するのには僕のPCで13秒ほどかかりました。
そのうえ、精度についても保証はされていません。仮設は正しいようだとは言ったものの、証明したわけでもないですし。だから正確には素数判定機ではなく、”素数判定機かもしれないプログラム”でしかありません。もし証明できる人や反例を見つけた人がいれば是非教えてください。
実用的な素数判定機については、「決定的素数判定法/確率的素数判定法」「AKS素数判定法」「ミラーラビン素数判定法(Miller-Rabin primality test)」などで検索してみてください。
おわりに
さて、入試数学の問題を用いてプログラムを書いたわけですが、プログラミング初心者の僕にはこれがかなり良い練習になりました。手計算で解く時の手順を参考に、for文でループしたり配列を使ったりという基本文法を覚えられるだけでなく、一度に大量に書くと訳分からなくなるためまずは余りを足しあげる機能だけやってみて…というようにコードを組み立てていく練習にもなりました。
初心者向けのコード練習の有名どころとしてはFizzBuzzなどがありますが、素数判定とか最大公約数とかのように数学的な性質を利用した問題にも是非挑戦してみてください。
追記/訂正
仮説にて、
素数pに対して、(1n+2n+3n+・・・+ (p-1)n)をpで割った余りは、nが(pの倍数-1)の時以外は0になり、nが(pの倍数-1)の時には(p-1)となる。
と述べていますが、これが誤りであったことが判明しました。
「nが**(pの倍数-1)の時以外は」ではなく、「nが(p-1)の倍数**の時以外は」とすれば正しいようです。
実際に、n=1,2,3,...に対して1n+2n+3n+・・・+ (p-1)n を7で割った余りを並べると、0,0,0,0,0,6,0,0,0,0,0,6,0,0,0,0,0,6,0,0,0,0,0,6...と、6の倍数の時のみ6となることが確認できました。
コメントありがとうございました。