こんにちは.九州大学工学府航空宇宙工学専攻修士2年,ITストラテジストの岩附陽太です.
TAで飛行力学1の採点補助をしていて,間違いが多かった「航空機の最大上昇時は抗力最小ではない」という話をしたいと思います.
問題
各自選んだ機体について,海面標準状態における最大上昇率と,その時の速度を求めなさい.ジェット機の場合には推力は速度によらず一定と過程し,プロペラ機の場合には,(一般には正しくないが計算のために)利用パワー=エンジン軸パワー×0.8と仮定し,速度によらず一定と仮定しなさい.ただし,経路角が微小であるという仮定を用いてよい.
基本となる式
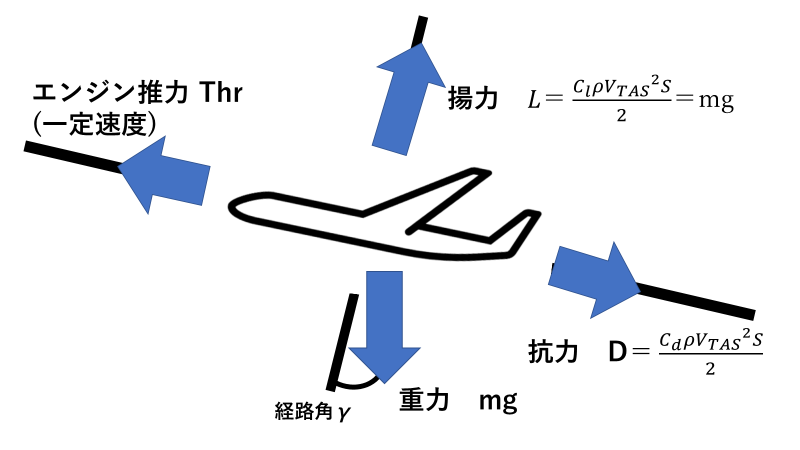
揚力と重力の一部が釣り合っており,一定であると仮定します.つまり,以下のような状況ですね.
$$L=mgcos(\gamma)$$
$$m\dot{V}_{TAS}=Thr-D-mgsin(\gamma)$$
ここで速度一定であるとします.ここの詳しい議論は最下部のBADAによる捕捉で説明しておきます.速度一定なので,
$$0=Thr-D-mgsin(\gamma)$$
この2式から
$$tan(\gamma)=\frac{sin(\gamma)}{cos(\gamma)}=\frac{(\frac{Thr-D}{mg})}{(\frac{L}{mg})}=\frac{Thr-D}{L}$$
また,このシチュエーションでは経路角が微小であると仮定しています.なので,$sin(\gamma)$,$cos(\gamma)$はこうなります.
$$cos(\gamma)=1$$
(このとき$L=mg$なので)
$$sin(\gamma)=tan(\gamma)=\frac{Thr-D}{L}=\frac{Thr-D}{mg}$$
この時に上昇率について考えます.速度はエンジン推力方向にしかないので,$ROC$(Rate of Climb)は以下の式になります.
$$ROC=\dot{Alt}=V_{TAS}sin(\gamma)=\frac{V_{TAS}(Thr-D)}{mg}$$
模範解答
まず抗力$D$は,大気密度を$\rho$,翼面積を$S$とすれば
$$D=C_{D} \rho V^{2}_{TAS}S$$
抗力係数$C_{D}$は,以下の式となる.$e$は飛行機効率,$AR$はアスペクト比です.この式になることが謎な人は銀本(牧野光雄著:航空力学の基礎)の3章や4章を見てください.BADAもこのモデルを使ってますね.
$$C_{D}=C_{d0}+\frac{C_{L}^{2}}{\pi e AR}$$
そして,$C_{L}$今,$L=mg$とすれば,
$$C_{L} \rho V^{2}_{TAS}S=mg$$
$$C_{L}=\frac{mg}{\rho V^{2}_{TAS}S}$$
よって,
$$C_{D}=C_{d0}+\frac{(\frac{mg}{\rho V^{2}_{TAS}S})^{2}}{\pi e AR}$$
$$D=C_{d0} \rho V^{2}S+\frac{(mg)^{2}}{\pi e AR\rho V^{2}S}$$
($V_{TAS}$でなく,$V$である理由はQiitaの数式がなぜか反応しなかったためです.同じ意味です.)
よって,
$$\dot{Alt}=\frac{VThr}{mg}-\frac{C_{d0} \rho V^{3}S}{mg}-\frac{mg}{\pi e AR\rho VS}$$
この時間の変数を$V$のみと仮定する.時間微分は,以下の式になる.
$$\ddot{Alt}=\frac{Thr}{mg}-\frac{3C_{d0} \rho V^{2}S}{mg}+\frac{mg}{\pi e AR\rho V^{2}S}$$
よって,$V^{2}$のみの関数とみなせる.
$\lim_{V→\infty}(\dot{Alt})=-\infty$かつ,$V=0$で$\dot{Alt}=0$であり,航空機を設計するうえで,$\dot{Alt}$が正になりえないわけはないと考えれば,$Thr_{MAX}$で少なくとも$\dot{Alt}$は正になりえて,$Thr_{MAX}$の中で極大となる値が$\dot{Alt}$の最大となる.
よって極大値を求めるために$\ddot{Alt}$=0を考えると,
$$\frac{3C_{d0} \rho S}{mg}V^{4}-\frac{Thr}{mg}V^{2}-\frac{mg}{\pi e AR\rho S}=0$$
2次方程式の解の公式から,
$$V^{2}=\frac{\frac{Thr}{mg}\pm\sqrt{(\frac{Thr}{mg})^{2}+4(\frac{3C_{d0} \rho S}{mg})(\frac{mg}{\pi e AR\rho S})}}{2(\frac{3C_{d0} \rho S}{mg})}$$
実数解を考えると$V^{2}\geq0$より,
$$V^{2}=\frac{\frac{Thr}{mg}+\sqrt{(\frac{Thr}{mg})^{2}+4(\frac{3C_{d0} \rho S}{mg})(\frac{mg}{\pi e AR\rho S})}}{2(\frac{3C_{d0} \rho S}{mg})}$$
よって$\dot{Alt}$の極大値を与える$V$は,
$$V=\sqrt{\frac{\frac{Thr}{mg}+\sqrt{(\frac{Thr}{mg})^{2}+4(\frac{3C_{d0} \rho S}{mg})(\frac{mg}{\pi e AR\rho S})}}{2(\frac{3C_{d0} \rho S}{mg})}}$$
であり,$Thr=Thr_{MAX}$かつこの極大の時$\dot{Alt}$最大であるから,
$$\dot{Alt_{MAX}}=\frac{Thr}{mg}(\sqrt{\frac{\frac{Thr_{MAX}}{mg}+\sqrt{(\frac{Thr_{MAX}}{mg})^{2}+4(\frac{3C_{d0} \rho S}{mg})(\frac{mg}{\pi e AR\rho S})}}{2(\frac{3C_{d0} \rho S}{mg})}})-\frac{C_{d0} \rho S}{mg}(\sqrt{\frac{\frac{Thr_{MAX}}{mg}+\sqrt{(\frac{Thr_{MAX}}{mg})^{2}+4(\frac{3C_{d0} \rho S}{mg})(\frac{mg}{\pi e AR\rho S})}}{2(\frac{3C_{d0} \rho S}{mg})}})^{3}-\frac{mg}{\pi e AR\rho S}(\sqrt{\frac{\frac{Thr_{MAX}}{mg}+\sqrt{(\frac{Thr_{MAX}}{mg})^{2}+4(\frac{3C_{d0} \rho S}{mg})(\frac{mg}{\pi e AR\rho S})}}{2(\frac{3C_{d0} \rho S}{mg})}})^{-1}$$
$$V_{MAX}=\sqrt{\frac{\frac{Thr_{MAX}}{mg}+\sqrt{(\frac{Thr_{MAX}}{mg})^{2}+4(\frac{3C_{d0} \rho S}{mg})(\frac{mg}{\pi e AR\rho S})}}{2(\frac{3C_{d0} \rho S}{mg})}}$$
具体例
Boeing777-200の海面標準状態の最大$ROC$ついて調べる.データはBADAより引用.
質量$m=247,210kg$(最大離陸重量)
主翼面積$S=427.82(m^{2})$
スパン$b=60.93(m)$
アスペクト比$AR=\frac{b^{2}}{S}=8.678$
エンジン最大推力$Thr_{MAX}=335.5kN$×2 (GE90-76B×2発)
$C_{d0}=0.02$
$e=0.8$
$\rho=1.225(kg/m^{3})$
$g=9.8(m/s^{2})$
$\dot{Alt_{MAX}}=25.53437003070827(m/s)$
$V_{MAX}=148.58875879283445(m/s)$
import math
import matplotlib.pyplot as pyplot
m=247210
S=427.82
AR=8.678
ThrMax=335.5*2*(10**3)
Cd0=0.02
e=0.8
rho=1.225
g=9.8
#解の公式で使う係数から解く
a=(3*Cd0*rho*S)/(m*g)
b=-(ThrMax)/(m*g)
c=-(m*g)/(math.pi*e*AR*rho*S)
Vmax=math.sqrt((-b+math.sqrt(b*b-4*a*c))/(2*a))
ROCmax=(ThrMax*Vmax)/(m*g)-(Cd0*rho*S*(Vmax**3))/(m*g)-(m*g)/(math.pi*e*AR*rho*Vmax*S)
print(Vmax)
print(ROCmax)
可視化して調べる
まず,
$$\dot{Alt}=\frac{V_{TAS}(Thr-D)}{mg}=\frac{P_{available}-P_{required}}{mg}$$
と考えます.これはつまり,
$$P_{available}=VThr$$
$$P_{required}=VD$$
と考えるのと同じことです.そして$P_{required}$最小の時は,抗力最小を$D_{min}$とし,$mg=L=Const$の近似を考えると,$D/L$最小は$D_{min}$であるので,
$$y=D_{min}V$$
という揚抗比最大の直線に接する点になります.B772のフライトエンベロープは以下の図になるので,高度0mなら真大気速度は90m/sから170m/sが入っている領域を離散化すればよさそうです.(1knotは約0.5m/sです)
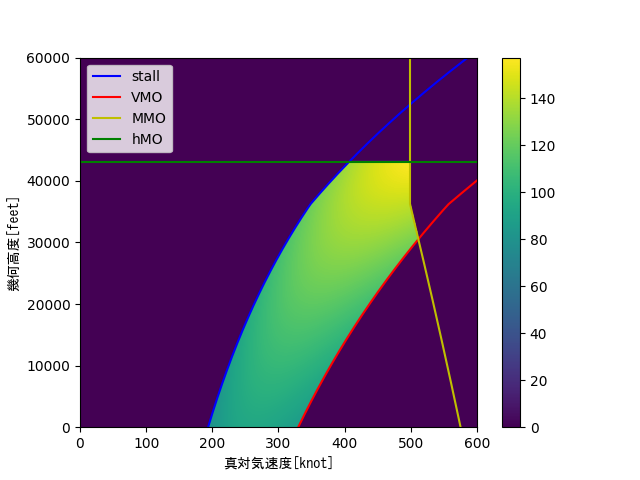
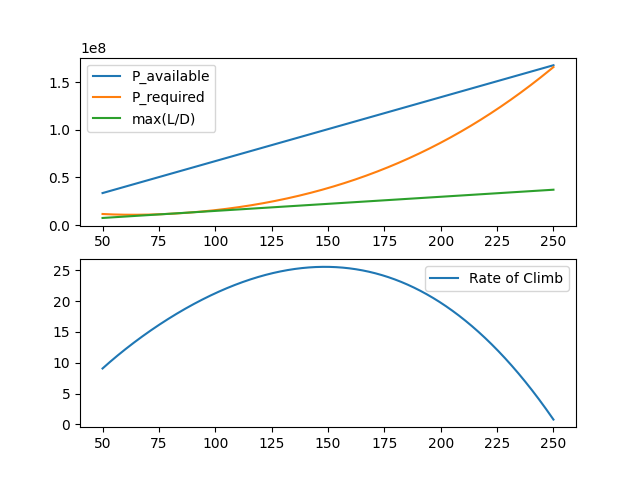
これらを踏まえて可視化すると以下になります.
出力結果はこれです.
ROCmax: 25.53437003059231 ROCmaxv: 148.589
p_rqmin: 13346465.129672157 p_rqminv: 90.0
Dmin: 148294.0569963573 Dminv: 90.0
最大上昇時は抗力最小ではありません.フライトエンベロープからもわかる通り,抗力最小の時はできるだけ燃料を使わない飛び方で,およそ失速速度付近での飛行になります.対し,最大上昇の時はエンジンをもっと吹いて,頑張って飛ぶ飛び方になります.
可視化に用いたプログラム
Vmin=50
Vmax=250
Len=int(Vmax-Vmin)*1000
v_List=list()
p_av_List=list()
p_rq_List=list()
ROC_List=list()
for i in range(Len):
v=Vmin+i/Len*(Vmax-Vmin)
p_av=ThrMax*v
p_rq=(Cd0*rho*S*(v**3))+((m*g)**2)/(math.pi*e*AR*rho*v*S)
ROC=(p_av-p_rq)/(m*g)
D=p_rq/v
v_List.append(v)
p_av_List.append(p_av)
p_rq_List.append(p_rq)
ROC_List.append(ROC)
if v==90:
Dminv=v
Dmin=D
p_rqminv=v
p_rqmin=p_rq
ROCmaxv=v
ROCmax=ROC
else:
if Dmin>D:
Dminv=v
Dmin=D
if p_rqmin>p_rq:
p_rqminv=v
p_rqmin=p_rq
if ROCmax<ROC:
ROCmaxv=v
ROCmax=ROC
DminLineList=list()
for i in range(Len):
v=Vmin+i/Len*(Vmax-Vmin)
DminLineList.append(Dmin*v)
fig=plt.figure()
ax1=fig.add_subplot(2,1,1)
ax1.plot(v_List,p_av_List,label='P_available')
ax1.plot(v_List,p_rq_List,label='P_required')
ax1.plot(v_List,DminLineList,label='max(L/D)')
ax1.legend()
ax2=fig.add_subplot(2,1,2)
ax2.plot(v_List,ROC_List,label='Rate of Climb')
ax2.legend()
plt.savefig('Test1.png')
print('ROCmax:',ROCmax,' ','ROCmaxv:',ROCmaxv)
print('p_rqmin:',p_rqmin,' ','p_rqminv:',p_rqminv)
print('Dmin:',Dmin,' ','Dminv:',Dminv)
よくあった間違い
・推力一定と,パワー一定を間違えている.
・最大上昇時が抗力最小だと思っている.
・パワーが速度の関数であることに気づいていない.
・Dが速度の関数であることに気づいていない.
・微分を用いないで解く中で,離散化が甘い.
.そもそも$MAX(VThr-DV)$を解く議論の中で,$MIN(DV)$に問題をすり替えており,本人がすり替わったことに気づいていない.
・最大推力でなく,なぜか巡航速度の推力を用いている.その結果$ROC=3(m/s)$になっている.どうやって上昇するんだその飛行機.
コメント
九大は入試方式が変わって推薦が増えたり数学で差がつかなくなったと聞きますが,合成関数の微分や,この数が時間の変数なのか定数なのかの判別みたいな部分が弱い人が増えてる気がします.(半面プログラミングができる人は増えてそうです.)数学力をちゃんと鍛えましょう.
また,物理的に考えても失速速度付近の飛行がROC最大になるわけなくないですか?失速速度は前のレポートで求めたと思うので,妥当性の検証をしましょう.
僕らM2は学部1年の前期で近藤先生という振動の権威の先生に,「物理を極めてください.覚悟の無いものは去れ,それが君たちのためであり世の中のためである」と言われました.
エンジニアのミスは,自動車事故や航空機事故につながり,人を殺します.中途半端な覚悟で工学をやるなという意味でした.
課題4は全体的に,計算できればいい,結果だけ貼ればよい,みたいなおざなりなレポートが多かったです.ぜひ改めてほしいと思います.(特にプログラミングができる人,コードだけ貼るのはレポートとはいいません.)
BADAによる理論の捕捉
現実問題,航空機の上昇時は$\gamma=15[degree]$程度と微小でない値をとる場合もあるので,そもそも$ROC$の式自体,ある種の参考ととらえてもらった方がよいでしょう.実際の値は微小擾乱の運動方程式で速度一定となる制約条件のもと様々なパターンを与えてやれば,求まると思います.(いずれ確かめようと思います.)しかし,別の側面からも,$ROC$がある程度参考になるか確かめておきます.
まず航空機の縦のエネルギー式モデルは以下です.左辺が外部からの仕事(力×速度×時間の次元ですね),右辺が運動エネルギーと位置エネルギーですね.
$$ \int_{0}^{t_{max}}(Thr(t)-D(t))V_{TAS}(t)dt=\frac{1}{2}m(t)V_{TAS}(t)^{2}+m(t)gAlt(t) $$
ほんとは推力と抗力以外の力や,重力加速度も変化しますがいったん無視します.これだと式が複雑すぎるので,$Thr(t)-D(t)$の時間変化,航空機質量$m(t)$の時間変化,を微小として無視します.この仮定の上でさっきの式を微分すると,BADAで紹介されているパワー(エネルギー÷時間次元)のつり合い式になります.
$$ (Thr-D)V_{TAS}=mV_{TAS}\dot{V_{TAS}}+mg\dot{Alt} $$
これを$\dot{Alt}$について整理すればBADAの文脈における上昇率の式になります.
$$ \dot{Alt}=\frac{(Thr-D)V_{TAS}}{mg}-\frac{V_{TAS}\dot{V_{TAS}}}{g} $$
式を見ればわかるように,瞬間的に速度を犠牲にして高度を稼ぐことは瞬間的に可能です.これは紙飛行機などがいったん上を向いて,失速するのと同じです.しかし一般に最大上昇率を求めたいときは離陸後の高度を稼ぎたいときなどであると考えると,失速するようなシチュエーションを考えるのは非現実的なので,速度は一定とします.するとさっきの式は,
$$ \dot{Alt}=\frac{(Thr-D)V_{TAS}}{mg} $$
という飛行力学でよく見る$ROC$の式になります.