あけましておめでとうございます.九大航空修士2年,ITストラテジストの岩附陽太です.やっと修論の第一稿が終わりましたので,この隙にネタを投下していきたいと思います.
今回は,破壊モード1,モード2における応力場,変位場の可視化を行います.
前提条件
・筆者は破壊力学が専門ではありません.間違いがありましたらすいません.修正しますのでご連絡ください.
・以下の資料を参考にします.
[1]岡部朋永 応用解析からはじめる弾性力学入門 コロナ社
[2]北海道大学 破壊力学講義資料
https://www.eng.hokudai.ac.jp/labo/bridge/staff/matsumoto/FractureOfFiberComposite_Chapter3.pdf
[3]安中特殊硝子製作所 石英ガラス
https://annaka-tg.com/wordpress_5/wp-content/uploads/vitreous.pdf
・使う式に関しては記載し式の導出過程を飛ばします.資料[1]が詳しいです.式も取り扱えますが,大量の数式を書くモチベがありません.需要がありましたら全体的にクオリティを上げますのでコメントください.
・プログラミングコードは記載します.
・特別講義を受けたことがきっかけです.特別講義では応力場,変位場の式の導出が課題でしたが+αとしてプログラムでの可視化をやってみたので,せっかくならQiitaに上げようということです.
破壊力学とは
破壊力学とは,亀裂の周辺や,金属疲労,脆性破壊など,材料が壊れる周辺の力学を取り扱う学問です.従来の材料力学では取り扱えないような事象について取り扱う,第一次大戦以降で発展した比較的新しい分野になります.
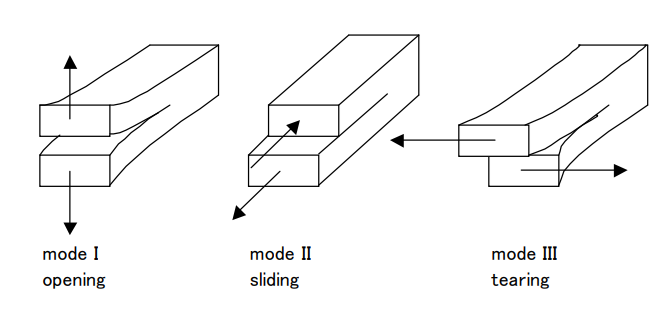
破壊モードについて
モード1は割りばしを割るときや材料の破壊でよく起こります.
モード2は地震の断層の破壊や繊維シートの剥離で起こります.
モード3はお菓子屋醤油の袋を破るときに用います.
本記事ではモード1,モード2について取り扱います.
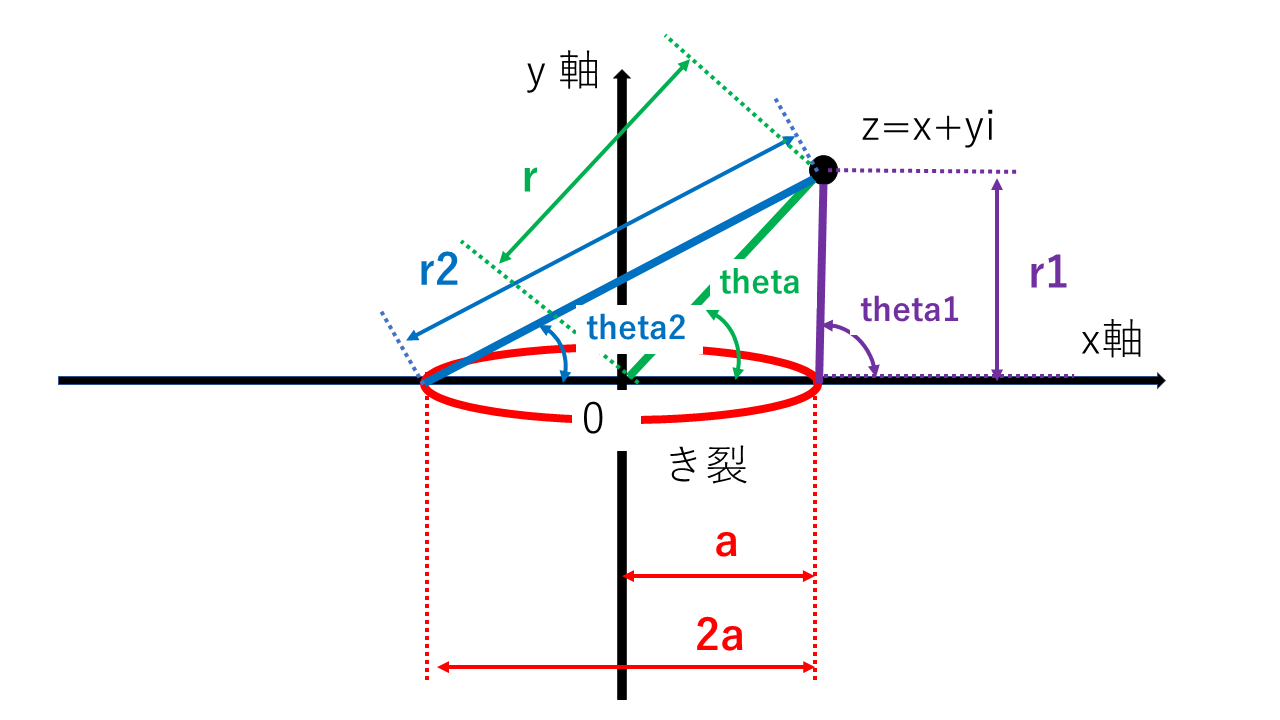
き裂周辺に導入される座標系について
式の導出方法
1:エアリの応力関数を複素数が入った形で定義
2:エアリの応力関数は平衡方程式の解となる重調和関数なので,応力をエアリの応力関数で表せる.
3:2次元ひずみにおける応力関係式に代入する.なお代入時にコーシーリーマンの関係を用いた計算の工夫が必要
4:モード1の場合はウェスタガートの関数,モード2の場合はアーウィンの関数を導入する.
5:3つの極座標を導入する.これにより,ウェスタガートの関数,アーウィンの関数がオイラーの公式を用いて実部虚部に分解できるシンプルな形になり,容易に積分,微分も計算できる.
6;2で行った応力の式に5の極座標系で計算した複素関数を代入して応力場を得る.
7:3で4で行った応力ひずみ関係式に5の極座標系で計算した複素関数を代入してひずみ場を得る.
8:ひずみ場を積分して変位場を得る.合成関数の積分であることに注意し,合成関数の微分をした際にひずみ場になることを確認するとよい.
可視化の際に共通で用いるパラメーター
まず適当なガラスであるとして,参考資料[3]より,横弾性係数$G=3232[kgf/{mm}^2]=3.16736×10^{10}[Pa]$とします.平面ひずみ,平面応力で異なる$\kappa$を計算するために用いるポアソン比$\upsilon$も参考資料[3]より0.16とすします.
平面ひずみの際,$\kappa=3-4\upsilon$,平面応力の際,$\kappa=\frac{3-\upsilon}{1+\upsilon}$となります.
き裂の大きさなどは特に特定の場合を考えるわけではないので,メッシュは-20.5mmから20.5mmまで1mm間隔とし,平面ひずみ状態であるとします.無限遠での,モード1の垂直応力は$\sigma^\infty={10}^{10}[Pa]$,無限遠でのモード2のせん断応力は$\tau^\infty={10}^{10}[Pa]$として,ひずみの幅の片側はa=10mmとしました.
プログラムはStateを変更することで,平面ひずみ状態にも平面応力状態にも使えるようにしました.平面ひずみは長い棒の断面,平面応力は薄い板の解析に適します.両方載せておいても冗長化かとおもったので,平面応力の場合のみこの記事では画像をのせておきます.
可視化の際に共通で用いるプログラムの関数
以下が共通で用いる関数やライブラリです.
import math
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
def CalcRT(x,y):
r=math.sqrt(x*x+y*y)#m
theta=math.atan(y/x)#rad
return r,theta
def CalcRT1(x,y,a):
x1=x-a
r=math.sqrt(x1*x1+y*y)#m
theta=math.atan(y/x1)#rad
return r,theta
def CalcRT2(x,y,a):
x2=x+a
r=math.sqrt(x2*x2+y*y)#m
theta=math.atan(y/x2)#rad
return r,theta
def CalcKappa(State,PoissonRate):
if State=='PlaneStrain':
Kappa=3-4*PoissonRate
elif State=='PlaneStress':
Kappa=(3-PoissonRate)/(1+PoissonRate)
else:
print('Error Check State')
Kappa=None
return Kappa
モード1の応力場について
モード1の応力場を司る式は以下になります.
$$\sigma_{x}=\frac{\sigma^{\infty}r}{\sqrt{r_{1}r_{2}}}cos(\theta-\frac{\theta_{1}+\theta_{2}}{2})-\frac{\sigma^{\infty}a^{2}}{(r_{1}r_{2})^{3/2}}rsin(\theta)sin(\frac{3(\theta_{1}+\theta_{2})}{2})$$
$$\sigma_{y}=\frac{\sigma^{\infty}r}{\sqrt{r_{1}r_{2}}}cos(\theta-\frac{\theta_{1}+\theta_{2}}{2})+\frac{\sigma^{\infty}a^{2}}{(r_{1}r_{2})^{3/2}}rsin(\theta)sin(\frac{3(\theta_{1}+\theta_{2})}{2})$$
$$\tau_{xy}=\frac{\sigma^{\infty}a^{2}}{(r_{1}r_{2})^{3/2}}rsin(\theta)cos(\frac{3(\theta_{1}+\theta_{2})}{2})$$
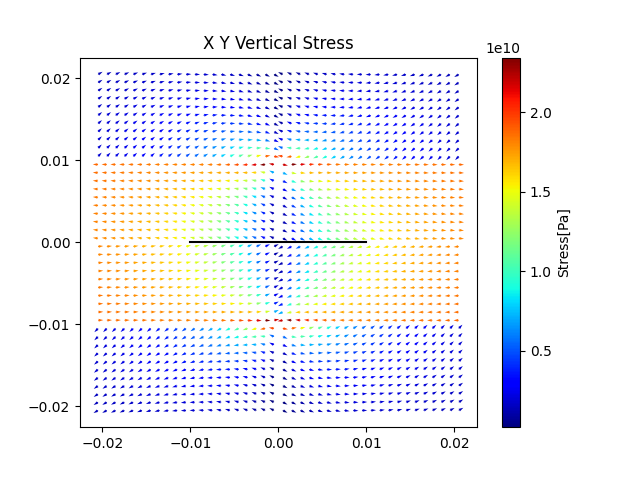
モード1の応力場の可視化結果
まず,垂直応力の応力場はこのようになります.向きは矢印で,大きさはカラーマップで表します.
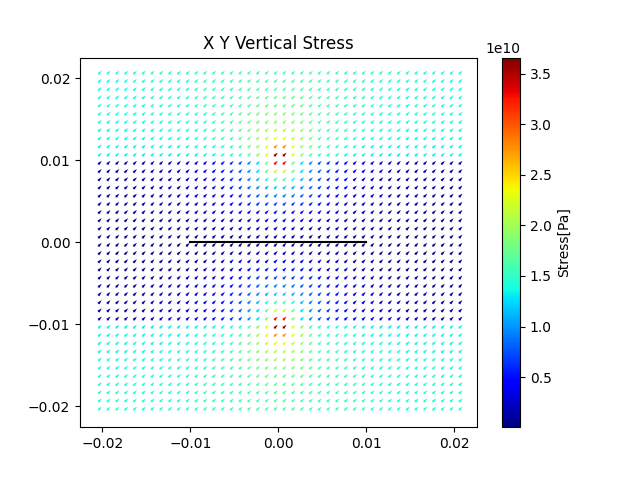
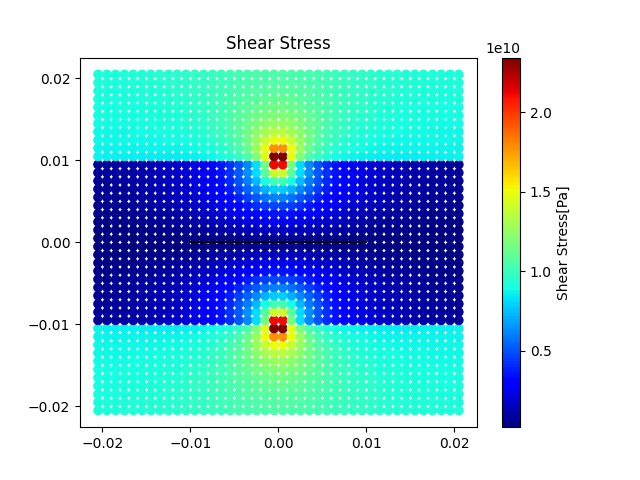
次にせん断応力の応力場を可視化します.+-含む形ですべてヒートマップとして表します.
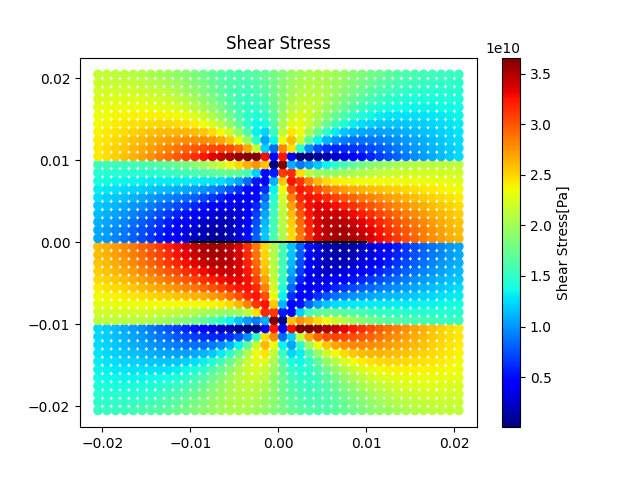
モード1の変位について
モード1の変位場を司る式は以下になります.uvはそれぞれx方向,y方向への変位です.
$2Gu=\frac{\kappa-1}{2}\sigma^{\infty}\sqrt{r_{1}r_{2}}cos(\frac{\theta_{1}+\theta_{2}}{2})-\frac{\sigma^{\infty}r}{\sqrt{r_{1}r_{2}}}rsin\theta sin(\theta-\frac{\theta_{1}+\theta_{2}}{2})$
$2Gv=\frac{\kappa+1}{2}\sigma^{\infty}\sqrt{r_{1}r_{2}}sin(\frac{\theta_{1}+\theta_{2}}{2})-\frac{\sigma^{\infty}r}{\sqrt{r_{1}r_{2}}}rsin\theta cos(\theta-\frac{\theta_{1}+\theta_{2}}{2})$
モード1の変位場の可視化結果
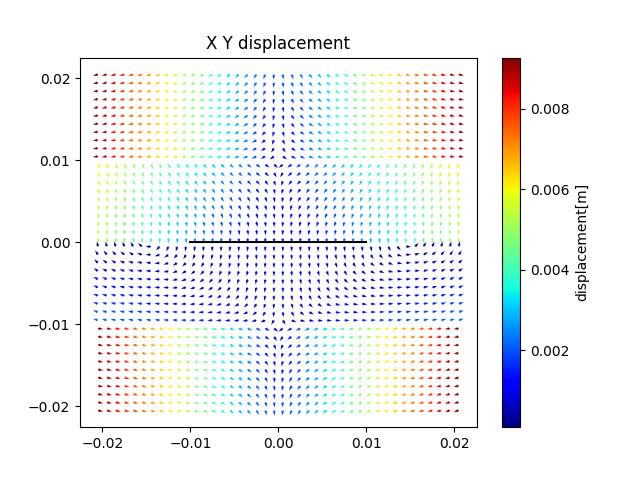
変位場の可視化結果は下図です.向きは矢印で,大きさはカラーマップで表します.
モード1の可視化プログラム
def CalcStress_Mode1(SigmaInf,r,theta,r1,theta1,r2,theta2,a):
sigmax=(SigmaInf*r)/(math.sqrt(r1*r2))*math.cos(theta-(theta1+theta2)/2)
-(SigmaInf*a*a)/((r1*r2)**(3/2))*r*math.sin(theta)*math.sin(3*(theta1+theta2)/2)
sigmay=(SigmaInf*r)/(math.sqrt(r1*r2))*math.cos(theta-(theta1+theta2)/2)
+(SigmaInf*a*a)/((r1*r2)**(3/2))*r*math.sin(theta)*math.sin(3*(theta1+theta2)/2)
tauxy=(SigmaInf*a*a)/((r1*r2)**(3/2))*r*math.sin(theta)*math.cos(3*(theta1+theta2)/2)
return sigmax,sigmay,tauxy
def CalcUV_Mode1(G,Kappa,SigmaInf,r,theta,r1,theta1,r2,theta2):
if r1*r2==0:
u=0
v=0
else:
u=((Kappa-1)/2*SigmaInf*math.sqrt(r1*r2)*math.cos((theta1+theta2)/2)
-r*math.sin(theta)*(SigmaInf*r)/(math.sqrt(r1*r2))*math.sin(theta-(theta1+theta2)/2) )/(2*G)
v=((Kappa+1)/2*SigmaInf*math.sqrt(r1*r2)*math.sin((theta1+theta2)/2)
-r*math.sin(theta)*(SigmaInf*r)/(math.sqrt(r1*r2))*math.cos(theta-(theta1+theta2)/2) )/(2*G)
return u,v
#Define Hyper Parameter
#Grrid Oeder=1mm
Len=42
Half=20.5
xlist=[(i-Half)/(1000) for i in range(Len)]#m
ylist=[(i-Half)/(1000) for i in range(Len)]#m
Xgrid,Ygrid=np.meshgrid(xlist, ylist)
SigmaXlist=[[0 for j in range(Len)] for i in range(Len)]#Pa
SigmaYlist=[[0 for j in range(Len)] for i in range(Len)]#Pa
TauXYlist=[[0 for j in range(Len)] for i in range(Len)]#Pa
Ulist=[[0 for j in range(Len)] for i in range(Len)]#m
Vlist=[[0 for j in range(Len)] for i in range(Len)]#m
C1list=[[0 for j in range(Len)] for i in range(Len)]#m
C2list=[[0 for j in range(Len)] for i in range(Len)]#m
G=3.16736*(10**10)#Pa
PoissonRate=0.16
State='PlaneStrain'
#State='PlaneStress'
Kappa=CalcKappa(State,PoissonRate)
SigmaInf=1*10**10#Pa
TauInf=1*10**10#Pa
#Crackwidth=10mm
a=0.01
#info
#https://qiita.com/sotatakahashi/items/fa8cbc5b3ea027ee754a
for i in range(0,Len):
if i%10==0:
print('Calculating:'+str(i)+'/'+str(Len))
for j in range(0,Len):
x=float(xlist[i])
y=float(ylist[j])
r,theta=CalcRT(x,y)
r1,theta1=CalcRT1(x,y,a)
r2,theta2=CalcRT2(x,y,a)
sigmax,sigmay,tauxy=CalcStress_Mode1(SigmaInf,r,theta,r1,theta1,r2,theta2,a)
SigmaXlist[i][j]=sigmax/math.sqrt(sigmax*sigmax+sigmay*sigmay)
SigmaYlist[i][j]=sigmay/math.sqrt(sigmax*sigmax+sigmay*sigmay)
TauXYlist[i][j]=tauxy
color1=math.sqrt(sigmax*sigmax+sigmay*sigmay)
C1list[i][j]=color1
u,v=CalcUV_Mode1(G,Kappa,SigmaInf,r,theta,r1,theta1,r2,theta2)
Ulist[i][j]=u/math.sqrt(u*u+v*v)
Vlist[i][j]=v/math.sqrt(u*u+v*v)
color2=math.sqrt(u*u+v*v)
C2list[i][j]=color2
fig1=plt.figure()
ax1=fig1.add_subplot(1,1,1)
Q=ax1.quiver(Xgrid,Ygrid,SigmaXlist,SigmaYlist,C1list,cmap='jet')
ax1.plot([-a,a],[0,0],color='black')
fig1.colorbar(Q, label='Stress[Pa]')
plt.title('X Y Vertical Stress')
plt.savefig('Result1.png')
fig2=plt.figure()
ax2=fig2.add_subplot(1,1,1)
ax2.plot([-a,a],[0,0],color='black')
XGlist=list()
YGlist=list()
TauGlist=list()
for i in range(0,Len):
XGlist.extend(Xgrid[i])
YGlist.extend(Ygrid[i])
TauGlist.extend(TauXYlist[i])
ax2.scatter(XGlist,YGlist,c=TauGlist,cmap='jet')
fig2.colorbar(Q, label='Shear Stress[Pa]')
plt.title('Shear Stress')
plt.savefig('Result2.png')
fig3=plt.figure()
ax3=fig3.add_subplot(1,1,1)
Q=ax3.quiver(Xgrid,Ygrid,Ulist,Vlist,C2list,cmap='jet')
ax3.plot([-a,a],[0,0],color='black')
fig3.colorbar(Q, label='displacement[m]')
plt.title('X Y displacement')
plt.savefig('Result3.png')
モード2の応力場について
モード2の応力場を司る式は以下になります.
$$\sigma_{x}=2\frac{\tau^{\infty}r}{\sqrt{r_{1}r_{2}}}sin(\theta-\frac{\theta_{1}+\theta_{2}}{2})-\frac{\tau^{\infty}a^{2}}{(r_{1}r_{2})^{3/2}}r_{1}sin(\theta_{1})cos(\frac{3(\theta_{1}+\theta_{2})}{2})$$
$$\sigma_{y}=\frac{\tau^{\infty}a^{2}}{(r_{1}r_{2})^{3/2}}r_{1}sin(\theta_{1})cos(\frac{3(\theta_{1}+\theta_{2})}{2})$$
$$\tau_{xy}=\frac{\tau^{\infty}r}{\sqrt{r_{1}r_{2}}}cos(\theta-\frac{\theta_{1}+\theta_{2}}{2})-\frac{\tau^{\infty}a^{2}}{(r_{1}r_{2})^{3/2}}r_{1}sin(\theta_{1})sin(\frac{3(\theta_{1}+\theta_{2})}{2})$$
モード2の応力場の可視化結果
モード2の変位について
モード2の変位場を司る式は以下になります.
$2Gu=\frac{\kappa+1}{2}\tau^{\infty}\sqrt{r_{1}r_{2}}sin(\frac{\theta_{1}+\theta_{2}}{2})+\frac{\tau^{\infty}r}{\sqrt{r_{1}r_{2}}}r_{1}sin\theta_{1} cos(\theta-\frac{\theta_{1}+\theta_{2}}{2})$
$2Gv=-\frac{\kappa-1}{2}\tau^{\infty}\sqrt{r_{1}r_{2}}cos(\frac{\theta_{1}+\theta_{2}}{2})-\frac{\sigma^{\infty}r}{\sqrt{r_{1}r_{2}}}r_{1}sin\theta_{1} sin(\theta-\frac{\theta_{1}+\theta_{2}}{2})$
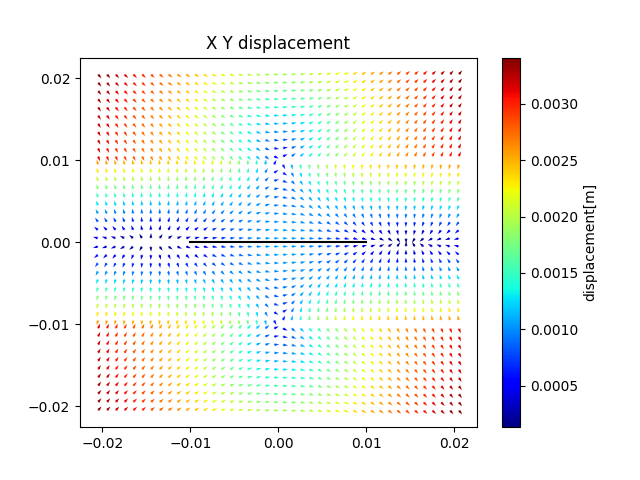
モード2の変位場の可視化結果
モード2の可視化プログラム
def CalcStress_Mode2(TauInf,r,theta,r1,theta1,r2,theta2,a):
sigmax=2*(TauInf*r)/(math.sqrt(r1*r2))*math.sin(theta-(theta1+theta2)/2)
-(TauInf*a*a)/((r1*r2)**(3/2))*r1*math.sin(theta1)*math.cos(3*(theta1+theta2)/2)
sigmay=(TauInf*a*a)/((r1*r2)**(3/2))*r1*math.sin(theta1)*math.cos(3*(theta1+theta2)/2)
tauxy=(TauInf*r)/(math.sqrt(r1*r2))*math.cos(theta-(theta1+theta2)/2)
-(TauInf*a*a)/((r1*r2)**(3/2))*r1*math.sin(theta1)*math.sin(3*(theta1+theta2)/2)
return sigmax,sigmay,tauxy
def CalcUV_Mode2(G,Kappa,TauInf,r,theta,r1,theta1,r2,theta2):
if r1*r2==0:
u=0
v=0
else:
u=((Kappa+1)/2*TauInf*math.sqrt(r1*r2)*math.sin((theta1+theta2)/2)
+r1*math.sin(theta1)*(TauInf*r)/(math.sqrt(r1*r2))*math.cos(theta-(theta1+theta2)/2) )/(2*G)
v=(-(Kappa-1)/2*TauInf*math.sqrt(r1*r2)*math.cos((theta1+theta2)/2)
+r1*math.sin(theta1)*(TauInf*r)/(math.sqrt(r1*r2))*math.sin(theta-(theta1+theta2)/2) )/(2*G)
return u,v
#Define Hyper Parameter
#Grrid Oeder=1mm
Len=42
Half=20.5
xlist=[(i-Half)/(1000) for i in range(Len)]#m
ylist=[(i-Half)/(1000) for i in range(Len)]#m
Xgrid,Ygrid=np.meshgrid(xlist, ylist)
SigmaXlist=[[0 for j in range(Len)] for i in range(Len)]#Pa
SigmaYlist=[[0 for j in range(Len)] for i in range(Len)]#Pa
TauXYlist=[[0 for j in range(Len)] for i in range(Len)]#Pa
Ulist=[[0 for j in range(Len)] for i in range(Len)]#m
Vlist=[[0 for j in range(Len)] for i in range(Len)]#m
C1list=[[0 for j in range(Len)] for i in range(Len)]#m
C2list=[[0 for j in range(Len)] for i in range(Len)]#m
G=3.16736*(10**10)#Pa
PoissonRate=0.16
State='PlaneStrain'
#State='PlaneStress'
Kappa=CalcKappa(State,PoissonRate)
SigmaInf=1*10**10#Pa
TauInf=1*10**10#Pa
#Crackwidth=10mm
a=0.01
#info
#https://qiita.com/sotatakahashi/items/fa8cbc5b3ea027ee754a
for i in range(0,Len):
if i%10==0:
print('Calculating:'+str(i)+'/'+str(Len))
for j in range(0,Len):
x=float(xlist[i])
y=float(ylist[j])
r,theta=CalcRT(x,y)
r1,theta1=CalcRT1(x,y,a)
r2,theta2=CalcRT2(x,y,a)
sigmax,sigmay,tauxy=CalcStress_Mode2(TauInf,r,theta,r1,theta1,r2,theta2,a)
SigmaXlist[i][j]=sigmax/math.sqrt(sigmax*sigmax+sigmay*sigmay)
SigmaYlist[i][j]=sigmay/math.sqrt(sigmax*sigmax+sigmay*sigmay)
TauXYlist[i][j]=tauxy
color1=math.sqrt(sigmax*sigmax+sigmay*sigmay)
C1list[i][j]=color1
u,v=CalcUV_Mode2(G,Kappa,TauInf,r,theta,r1,theta1,r2,theta2)
Ulist[i][j]=u/math.sqrt(u*u+v*v)
Vlist[i][j]=v/math.sqrt(u*u+v*v)
color2=math.sqrt(u*u+v*v)
C2list[i][j]=color2
fig1=plt.figure()
ax1=fig1.add_subplot(1,1,1)
Q=ax1.quiver(Xgrid,Ygrid,SigmaXlist,SigmaYlist,C1list,cmap='jet')
ax1.plot([-a,a],[0,0],color='black')
fig1.colorbar(Q, label='Stress[Pa]')
plt.title('X Y Vertical Stress')
plt.savefig('Result4.png')
fig2=plt.figure()
ax2=fig2.add_subplot(1,1,1)
ax2.plot([-a,a],[0,0],color='black')
XGlist=list()
YGlist=list()
TauGlist=list()
for i in range(0,Len):
XGlist.extend(Xgrid[i])
YGlist.extend(Ygrid[i])
TauGlist.extend(TauXYlist[i])
ax2.scatter(XGlist,YGlist,c=TauGlist,cmap='jet')
fig2.colorbar(Q, label='Shear Stress[Pa]')
plt.title('Shear Stress')
plt.savefig('Result5.png')
fig3=plt.figure()
ax3=fig3.add_subplot(1,1,1)
Q=ax3.quiver(Xgrid,Ygrid,Ulist,Vlist,C2list,cmap='jet')
ax3.plot([-a,a],[0,0],color='black')
fig3.colorbar(Q, label='displacement[m]')
plt.title('X Y displacement')
plt.savefig('Result6.png')
まとめ
破壊力学の応力場,変位について可視化してみました.モードごとの数式の類似性や,挙動の違いが面白いなと感じました.自分はシンクタンクで防災などの案件にも携わりたいなと考えているので,特にモード2について理解を深めていきたいです.(石川の震災について非常に心配しています)数式などは需要がありましたら書きたいと思いますので,コメントください.また,間違っている箇所などもありましたら指摘いただけますと幸いです.今年も何卒宜しくお願い致します.