背景
- ロジスティック回帰をする時にscikit-learnを用いていたが、何が行われているかきちんと理解できていなかったため、アルゴリズムの選定、パラメータのチューニングの判断根拠が乏しい。
対策
- scikit-learnを用いずにロジスティック回帰を実装し、仕組みを理解する。
データ
- データは、Kaggleのタイタニック（Titanic: Machine Learning from Disaster）を用いる。
概要
- タイタニックの生存者予測を行う。
- 特徴量は、理解しやすくするためAge（年齢）と、Fare（運賃）のみとする。
- 相関の強い性別を入れなかったのは、性別が離散値であるため図形として理解するときにやや不都合と考えるため。
ソース全量
ロジスティック回帰とは
ロジスティック回帰（ロジスティックかいき、英: Logistic regression）は、ベルヌーイ分布に従う変数の統計的回帰モデルの一種である。連結関数としてロジットを使用する一般化線形モデル (GLM) の一種でもある。1958年に David Cox が発表した[1]。確率の回帰であり、統計学の分類に主に使われる。医学や社会科学でもよく使われる。
- 回帰・分類・クラスタリングと課題の種類分けをした場合は、分類課題に対して有効。
- 分類を確率的に考える。
- すべての事象の同時確立が最大になるように最適化を行う。
実装
データの特徴
- データの中身
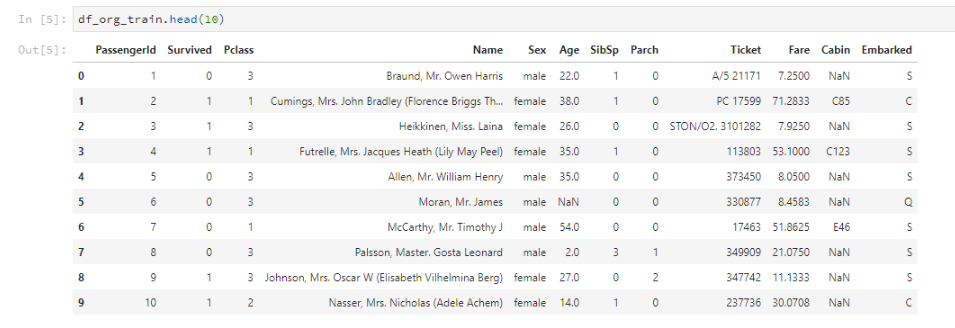
- PassengerId: 乗客のID
- Survived: 生死(0:死, 1:生)
- Pclass: チケットクラス（1 = 1st, 2 = 2nd, 3 = 3rd）
- Name: 名前
- Sex: 性別
- Age: 年齢
- SibSp: 兄弟や配偶者の数
- Parch: 親や子どもの数
- Ticket: チケットNo
- Fare: 料金
- Cabin: キャビン番号
- Embarked: 乗船場所（C = Cherbourg, Q = Queenstown, S = Southampton）
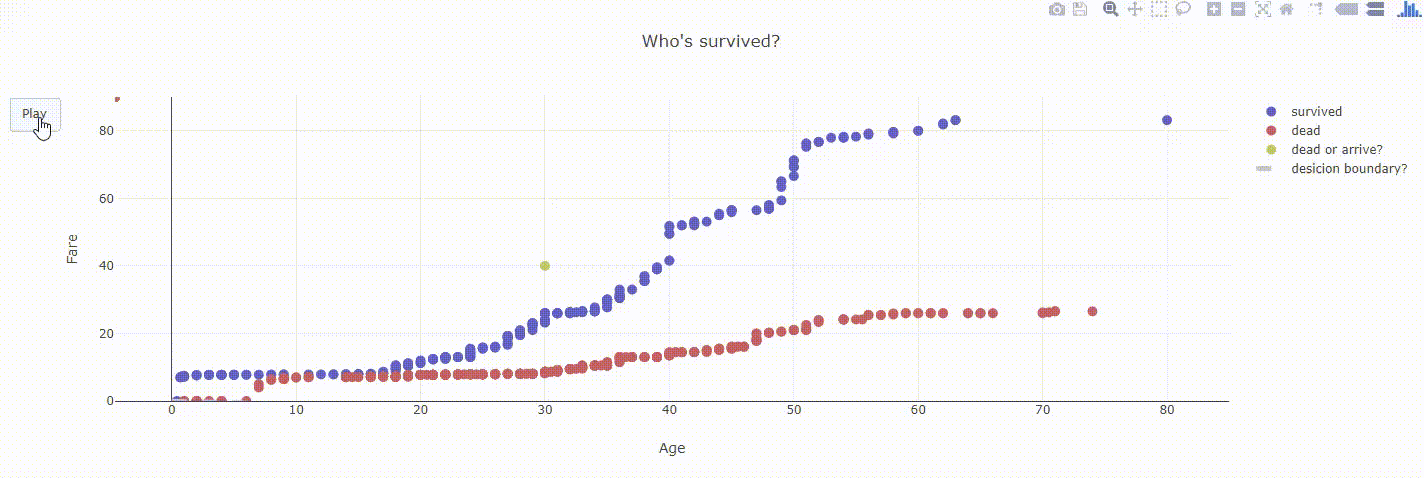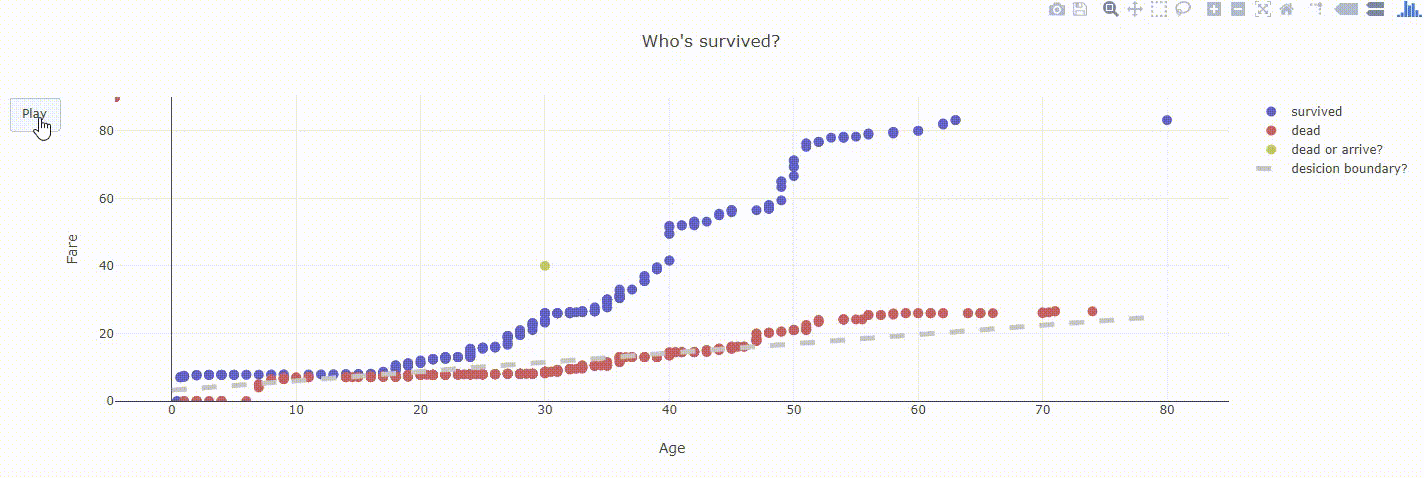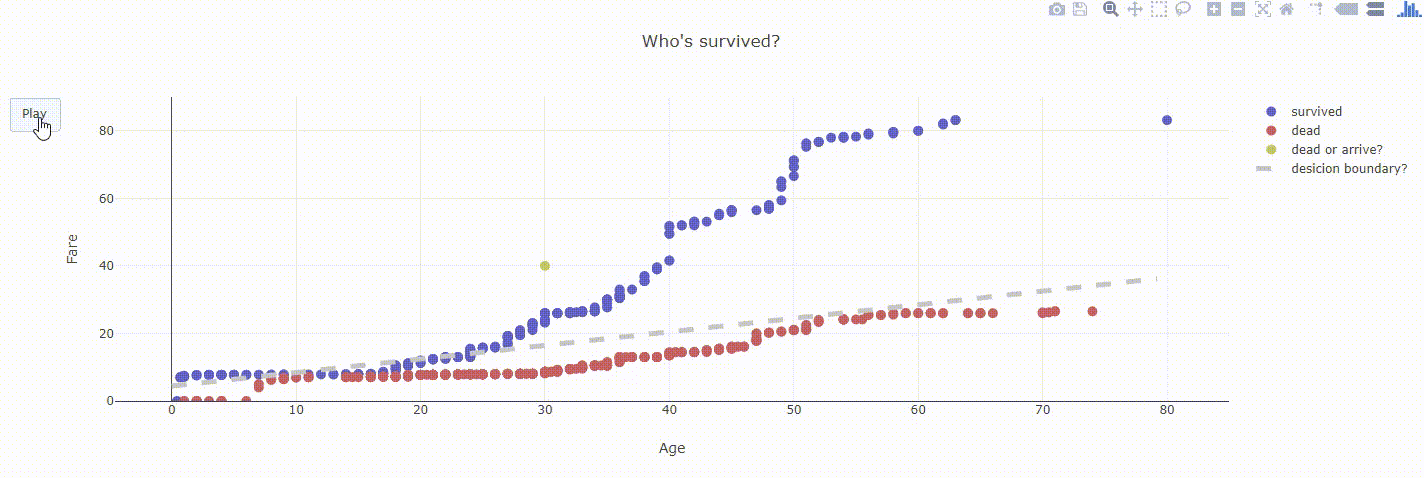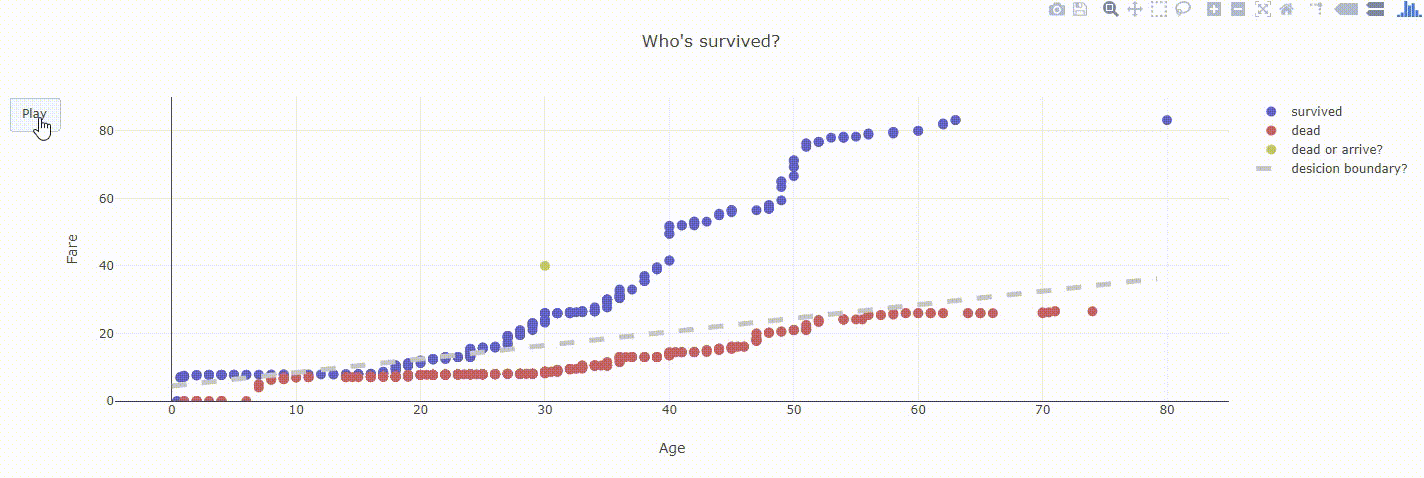
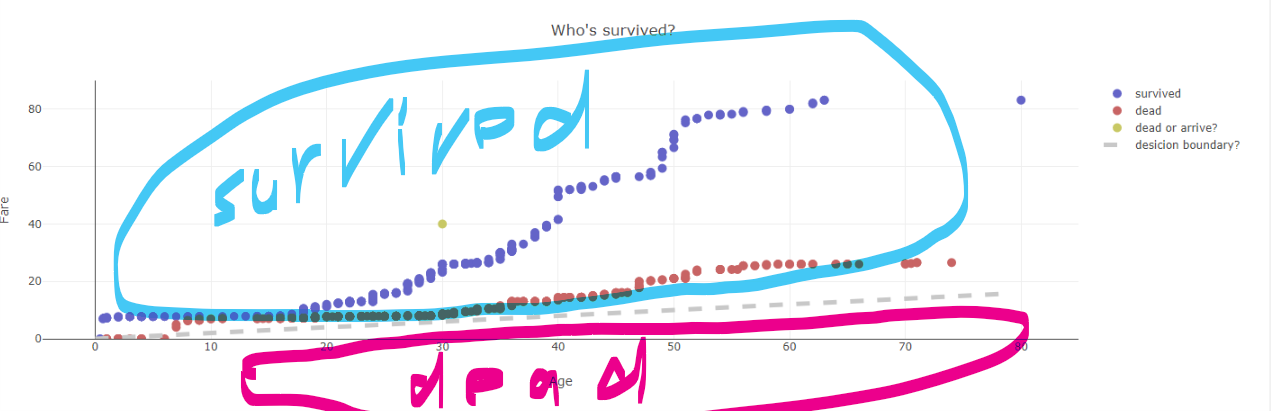
- Age、Fareに着目して、死んだ人を赤色、生き残った人を青色にしてグラフ化  - 年齢にかかわらず、運賃が高い人ほど生き残りやすいような傾向
- この生死を分かつ境界線を引くとしたら、このぐらいだろうか。これを**ロジスティック回帰**を用いて求める。そして新しい乗客（黄色のまる）が、生きるか死ぬかを予測する 
ロジスティック回帰
シグモイド関数
- ロジスティック回帰は確率的にとらえる。
- xを与えたとき、yになる条件付き確率で求める。
- P（確率）は0～1の値なので、シグモイド関数で求める。
- x(年齢、運賃)を与えたときに、y = 1（生き残る）確率
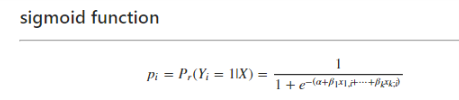
- 生き残る確率が0.5以上（50%以上）なら生、それ未満なら死とする。
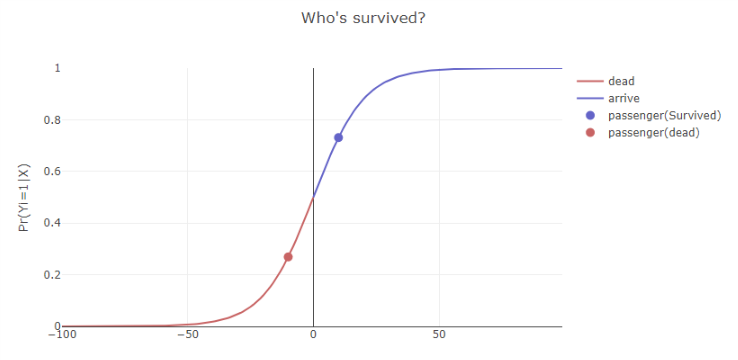
境界線
- exp(θT・x)=0のとき、1 / 1 + 1 = 0.5となる。
- すなわち、exp(θT・x)=0が境界となる。exp(θT・x)>0の範囲にある場合、生となる。（死はその逆）
- 今回は2次元なので、特徴量2つをx1, x2とし、x2についての解を求めてみる（可視化のため）。
- パラメータ（θ）を適当な値で初期化して、グラフ化してみる。
-- 境界線より上の部分が生、下が死となる。
-- いまは本来死となるべきデータが、生と分類されている。これは、パラメータを適当な値で初期化したためである。なので、ここからパラメータを最適化する必要がある。
最適化
- 何度も言うが、ロジスティック回帰は確率である。なので、それぞれが正しく分類される確率の同時確率が最大になるように最適化する。
- 式は以下の通り。同時確立（Π）の対数をとり（対数尤度関数）、それらを偏微分し、最後に符号を反転している（最急降下法と符号を合わせるため）。
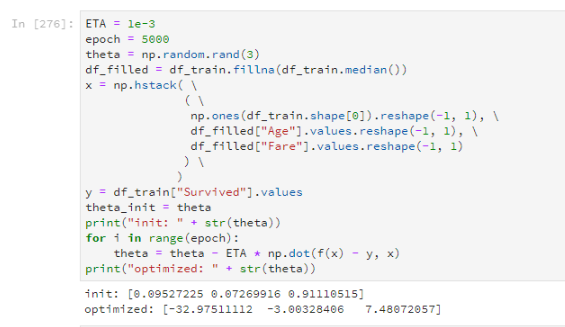
学習
- η（イータ、学習率）を1e-3、学習回数を5,000、θはランダムに初期化して学習。
- 大分フィットするようになったのがわかる（初期値から、最適化後のパラメータへのアニメーション）。 
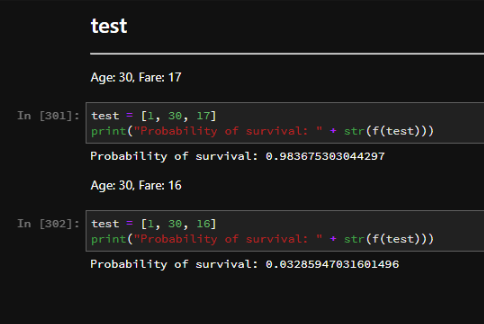
推測
- 同じ年齢の場合、運賃が高いほど生存率が高いことが分かる。
以上です。