この記事は古川研究室 Advent Calendar 22日目の記事です.
自分は古川研究室のOBなのですが,学生さんよりお誘いいただいて参加することになりました.よろしくお願いいたします.
はじめに
今回はscipy.sparseによる実装を併記しつつ,疎行列とその表現形式について説明したいと思います.
「numpyにはある程度慣れてきたけど疎行列関連はまだ手を出してなくて…どういうものなのか少しだけ知りたい!」という人向けの記事になります.
本記事では各表現形式がどのような値を用いて疎行列を表現しているのかについて着目して説明し,最後に簡単な実験としてメモリサイズと計算速度の比較を行います.
scipy.sparseについて本記事よりも詳しく知りたい場合はこちらをご参照ください.
https://docs.scipy.org/doc/scipy/reference/sparse.html
なお本記事はPythonのNumPyやSciPyを説明に用いますが,疎行列の概念や表現形式自体はこれらの言語やライブラリに限定されたものではなく,広く一般に使われているものです.
疎行列について
要素の多くがゼロとなっている行列は疎行列と呼ばれます.
疎行列は実データでよく現れます.例えばECサイトにある「どの人がどの商品をいくつ買ったか」というデータを愚直に行列表現しようとした場合,ユーザ総数×商品総数のドデカい行列に購入数を格納することになります.
この行列はもちろん大半の要素が0になってしまいます.
以下がそのイメージです(本来はもっとユーザ数・商品数が大きく,ゼロ要素の割合がずっと大きいです).
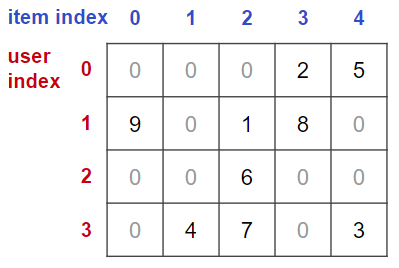
このデータをサンプルデータとして以降の説明をしていきます.
上記のデータはNumpy配列で以下のように作成できます.
import numpy as np
data_np = np.array([[0, 0, 0, 2, 5],
[9, 0, 1, 8, 0],
[0, 0, 6, 0, 0],
[0, 4, 7, 0, 3]])
しかしこのようにゼロ要素も含めて扱ってしまうとメモリ的にも演算的にも無駄が多くなってしまいます.
疎行列はゼロでない要素(非ゼロな要素・nonzeroな要素)のみに焦点をあてて情報表現すると効率的です.
疎行列には様々な表現形式があり,用途に応じて使い分ける必要があります.
本記事ではCOO形式, CSR形式, CSC形式のみに絞って,その情報表現方法と利点について紹介します.
(ちなみに一番活用されるのはCSR形式になるかと思います.)
本記事で説明していない初期化方法や利点・欠点などについて知りたい場合は以下をご参照ください.
https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.coo_matrix.html
https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csr_matrix.html
https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csc_matrix.html
COO形式
最も直観的な形式は座標形式(COOrdinate形式: COO形式)です.
疎行列を3つの1次元配列により表現します.
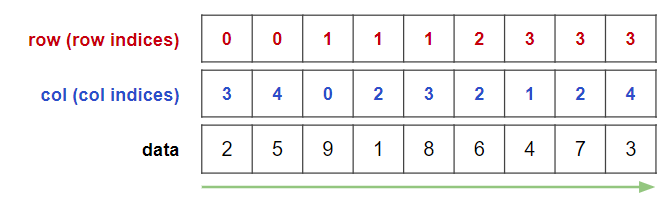
1つは非ゼロ要素の値を単に並べたものです.(COO形式自体は並べ順は自由ですが,scipy.sparseの挙動やのちの説明のため,本記事では図の緑線の順で並べます.)

残り2つは各非ゼロ要素の値がどのindexにあるのか示したものです.
この2つの配列により,非ゼロ要素の「座標」を表しています.
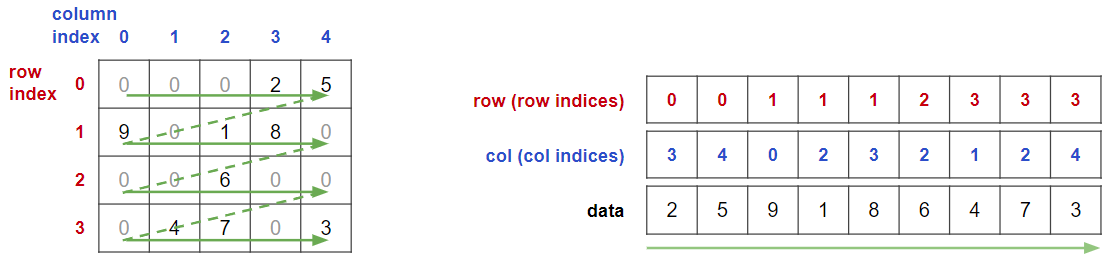
つまり,
0番ユーザが3番商品を2つ買っている
0番ユーザが4番商品を5つ買っている
1番ユーザが0番商品を9つ買っている
…
といった感じの情報表現になっています.
scipy.sparse.coo_matrix()を用いることで簡単にCOO形式に変換できます.
from scipy import sparse
data_coo = sparse.coo_matrix(data_np)
print(data_coo)
(0, 3) 2
(0, 4) 5
(1, 0) 9
(1, 2) 1
(1, 3) 8
(2, 2) 6
(3, 1) 4
(3, 2) 7
(3, 4) 3
図にある情報も表示してみます.
print(f"row: {data_coo.row}")
print(f"col: {data_coo.col}")
print(f"data: {data_coo.data}")
row: [0 0 1 1 1 2 3 3 3]
col: [3 4 0 2 3 2 1 2 4]
data: [2 5 9 1 8 6 4 7 3]
図に示した通りのデータが格納されていますね.
なおscipy.sparse.coo_matrix.todense()で通常の行列表現に戻せます.
print(data_coo.todense())
[[0 0 0 2 5]
[9 0 1 8 0]
[0 0 6 0 0]
[0 4 7 0 3]]
COO形式の利点
関係データベース的にも自然な表現であり,データセットとして提供されているデータもこのフォーマットが多いです.
例えば映画評価データであるMovieLens 100K Datasetも以下のように簡単にCOO形式で読み込めます.
import pandas as pd
df = pd.read_table('ml-100k/u.data', names=['user_id', 'movie_id', 'rating', 'timestamp'])
ml100k_coo = sparse.coo_matrix((df.rating, (df.user_id-1, df.movie_id-1)))
print(f'number of nonzero: {ml100k_coo.nnz}')
print(f'shape: {ml100k_coo.shape}')
number of nonzero: 100000
shape: (943, 1682)
MovieLens 100K Datasetは943人のユーザが1682個の映画に対し評価したデータで,非ゼロ要素が100000個なので,きちんと読み込めてそうですね.
(ただし,あくまで「非ゼロ要素以外には評価値0が入っている行列」となることには注意してください.「MovieLensのデータではこの行列の0の箇所は欠損値とみなして適切に取り扱う」といったようなデータ解析上の都合は,解析者側で適切に扱ってあげる必要があります.)
(あと実は先ほどのコードはcoo_matrixの引数周りで少し横着をしています.脱線になりますが丁寧バージョンが気になる場合はこちらの折りたたみを展開ください.)
MovieLens 100Kはuser_id, movie_idがたまたま連番になっているデータで,簡単にindexに変換できます
(具体的にはidが1から始まる連番になっているので,1引いて0から始まるようにすればindexのように扱えてしまう).
そういうラッキーなケースに頼らずにきちんとindexを作る場合は以下のようなコードになります.
import pandas as pd
df = pd.read_table('ml-100k/u.data', names=['user_id', 'movie_id', 'rating', 'timestamp'])
user_id_categorical = pd.api.types.CategoricalDtype(categories=sorted(df.user_id.unique()), ordered=True)
user_index = df.user_id.astype(user_id_categorical).cat.codes
movie_id_categorical = pd.api.types.CategoricalDtype(categories=sorted(df.movie_id.unique()), ordered=True)
movie_index = df.movie_id.astype(movie_id_categorical).cat.codes
ml100k_coo = sparse.coo_matrix((df.rating, (user_index, movie_index)))
また,COO形式はCSR形式やCSC形式への変換も高速です.
CSR形式
rowを見てみると,同じ数字が連続して並んでいることがわかります.
この情報をさらに圧縮した形式がCompressed Sparse Row形式: CSR形式と呼ばれる形式です.
(Compressed Row Storage形式: CRS形式とも呼ぶようです.直訳すると圧縮行格納形式ですね.)
どのように圧縮するかのイメージを説明します.
row の変わり目に区切り線を引いてみます.
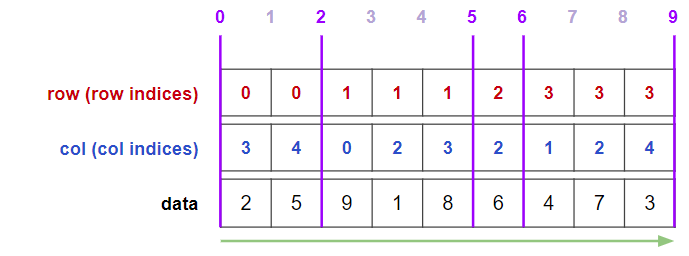
この区切り線の情報はrowの圧縮表現になっています.
ちょうど区切りに囲まれた部分がそれぞれ0行目,1行目,2行目,3行目の情報を表現していますね.
これをrowの代わりに用います.
以上をまとめると,CSR形式は以下の3つの1次元配列による表現になります.
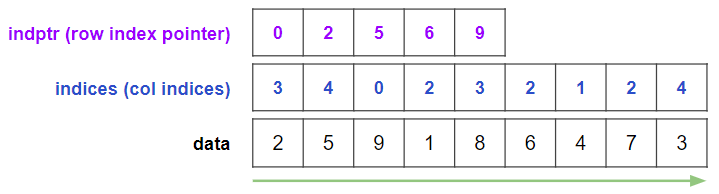
区切り線の情報はrow indicesの変化する箇所のポインタを集めたものになっているので,row index pointerと呼ばれます.
scipy.sparse.csr_matrixでは略してindptrという変数名になっています.
scipy.sparse.coo_matrix()と同じようにscipy.sparse.csr_matrix()で簡単に作成できます.
data_csr = sparse.csr_matrix(data_np)
print(f"index pointer: {data_csr.indptr}")
print(f"indices: {data_csr.indices}")
print(f"data: {data_csr.data}")
index pointer: [0 2 5 6 9]
indices: [3 4 0 2 3 2 1 2 4]
data: [2 5 9 1 8 6 4 7 3]
あるいはdata_csr = data_coo.tocsr()でも作成できます.
このように,scipy.sparse同士は.toxxx()というメソッドで相互に変換できます.
CSR形式の利点
行のスライスなど,行ごとに行われる処理が得意です.
最も利点が生きるのは行列積(明確に書くと,CSR形式疎行列とベクトルとの積)になります.
実装がどうなっているのか,中身を確認してみましょう.
https://github.com/scipy/scipy/blob/41800a2fc6f86446c7fe0248748bfb371e37cd04/scipy/sparse/sparsetools/csr.h#L1100-L1137
template <class I, class T>
void csr_matvec(const I n_row,
const I n_col,
const I Ap[],
const I Aj[],
const T Ax[],
const T Xx[],
T Yx[])
{
for(I i = 0; i < n_row; i++){
T sum = Yx[i];
for(I jj = Ap[i]; jj < Ap[i+1]; jj++){
sum += Ax[jj] * Xx[Aj[jj]];
}
Yx[i] = sum;
}
}
Apがrow index pointer,Ajがcolumn indices,Axが非ゼロデータ,
Xxが疎行列にかけるベクトルで,Yxが計算結果のベクトルです.
ゆっくり紙に書いてみるとわかるかと思いますが,CSR形式のそれぞれのデータが効率的に扱われています.
row index pointerによって各行の情報の範囲をうまく表現しており,column indicesによってかけられるベクトルの要素をピンポイントに持ってくることができています.
CSC形式
CSR形式における行と列の役割を入れ替えた表現になっています.
Compressed Sparse Column形式: CSC形式ということですね.
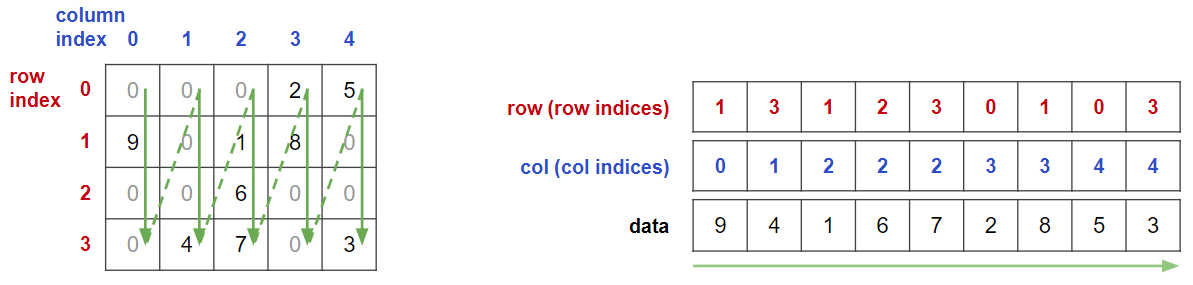
ほとんど繰り返しになりますが,一応どういう値が入っているのかを確認しておきましょう.
行列を緑線の順に読んでいき,COO形式にします.
colの変わり目の区切り線を考えます.
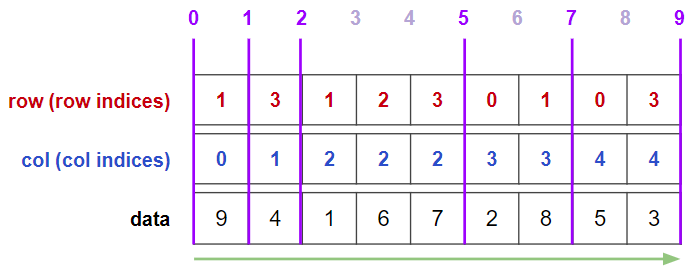
これをcol index pointerとし,colの代わりに用います.
よってCSC形式は以下のような表現になります.
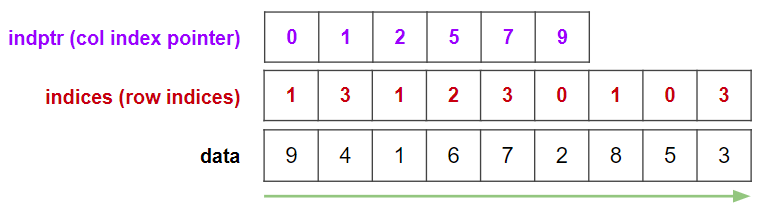
scipy.sparse.csc_matrix()で確認してみます.
data_csc = sparse.csc_matrix(data_np)
print(f"index pointer: {data_csc.indptr}")
print(f"indices: {data_csc.indices}")
print(f"data: {data_csc.data}")
index pointer: [0 1 2 5 7 9]
indices: [1 3 1 2 3 0 1 0 3]
data: [9 4 1 6 7 2 8 5 3]
確かに図示した通りの情報が格納されています.
CSC形式の利点
列スライスなどが得意です.
あと,CSR形式ほどではないですが,行列ベクトル積が早いようです.
メモリと計算時間の比較
ここまでに紹介した疎行列用の表現形式と,元の単純な行列表現について比較を行ってみましょう.
まずは先ほどCOO形式の利点の説明で用いたMovieLens 100K Datasetを使って,
各形式のメモリサイズ,特に配列の合計バイト数がどうなっているか確認してみます.
ml100k_csr = ml100k_coo.tocsr()
ml100k_csc = ml100k_coo.tocsc()
ml100k_np = ml100k_coo.todense()
print(f'np: {ml100k_np.nbytes}')
print(f'coo: {ml100k_coo.data.nbytes + ml100k_coo.col.nbytes + ml100k_coo.row.nbytes}')
print(f'csr: {ml100k_csr.data.nbytes + ml100k_csr.indices.nbytes + ml100k_csr.indptr.nbytes}')
print(f'csc: {ml100k_csc.data.nbytes + ml100k_csc.indices.nbytes + ml100k_csc.indptr.nbytes}')
np: 12689008
coo: 1600000
csr: 1203776
csc: 1206732
疎行列にあった表現形式になるとグッとメモリサイズが小さくなりますね.
このデータでは最も小さいメモリで済んでいるのは(僅差ですが)CSR形式ですね.
次に,ランダムな数値の入ったベクトルを右からかけてみて,行列ベクトル積の計算時間を測ってみます.
x = np.random.randint(1, 10, 1682)
%timeit ml100k_np @ x
%timeit ml100k_coo @ x
%timeit ml100k_csr @ x
%timeit ml100k_csc @ x
3.2 ms ± 20.1 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
159 µs ± 995 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
92.6 µs ± 1.48 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
140 µs ± 1.41 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
確かにCSR形式が最も早いようですね!
おわりに
疎行列の表現形式について説明し,簡易的に比較を行いました.参考になれば幸いです.
それでは良いスパースライフをお過ごしくださいませ!
なお,本記事の用いた環境は以下の通りです.
python = '3.7.0'
scipy = '1.3.3'
numpy = '1.17.3'
pandas = '0.25.3'