累積和について解説(C++)

この記事は高知工科大学 Advent Calendar 2018の23日目の記事です．
ここでは，累積和についてザックリ解説します．
※証明等はやりません．

#背景
去年のアドベントカレンダーで競プロを布教する記事を書きましたが，
次はレートが上がる楽しさを知ってもらいたいと思い，
AtCoder頻出かつ蟻本に無い累積和を紹介しようと思いました．

#累積和
整数配列の連続する区間の合計を，O(1)で求められる手法です．
(準備にO(配列の長さ)かかります)
主に，区間の合計を何度も求める際に使用します．
※配列の中身が変わってしまう場合には使えません．セグメント木を使いましょう

例えば配列の長さがN，区間の合計を求める回数がMの場合，
愚直に計算すると計算量はO(NM)になりますが，
累積和を使用するとO(N+M)になります．

##例題を使って解説
例題を解きながら学びます．
###問題文
整数N, Mが与えられます．
N回だけ整数A_iが与えられます．
M回だけだけ整数L, Rが与えられます．
区間A_LからA_Rの合計をそれぞれ求めてください．

####制約

\begin{align}
1 \leq N, M \leq 100000 \\
1 \leq L \leq R \leq N \\
1 \leq A_i \leq 10000 \\
\end{align}

####入力例
4 1
5 2 7 1
2 4
####出力例
10

###考え方
愚直に計算すると最悪計算量はO(NM)→O(10¹⁰)なので間に合いません．
累積和を使いましょう．

まず，長さN+1の配列を作り，1オリジンで入力します．

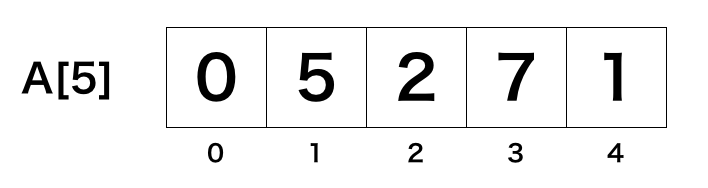
次に，配列を左から右に足していきます．

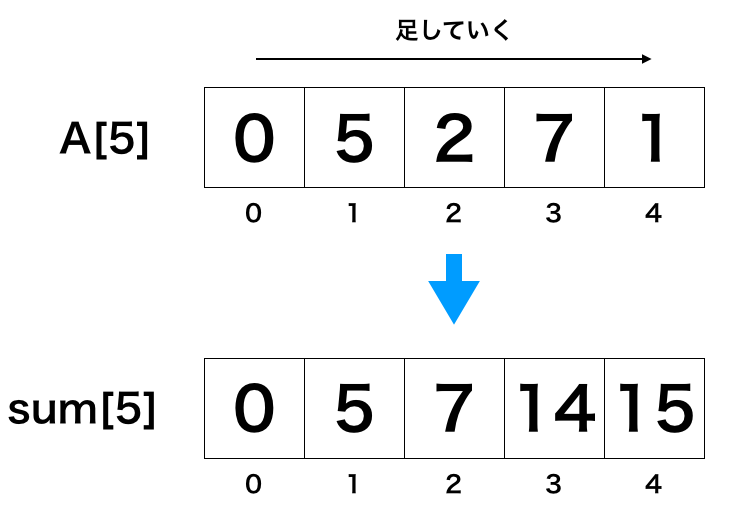
これで準備完了です．
最後に，求めたい領域の(右端)-(左端より1つ左側)をします．

これで求めたい領域の合計がすぐ求まります．

###ソースコード

#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
using namespace std;

int main() {
    int N, M, L, R;
    cin >> N >> M;
    int A[N+1]; A[0] = 0; // 1オリジン
    rep(i, N) cin >> A[i+1]; // input
    rep(i, N) A[i+1] += A[i]; // 累積和
    rep(i, M) {
        cin >> L >> R;
        cout << A[R] - A[L-1] << endl;
    }
    return 0;
}

##応用問題？
これを累積和と言っていいのか分からないですが，
左から右に足していく問題で良いのがあったので紹介します．
###問題文
机の上にリボンをいくつか重ね，ある場所に何個のリボンが重なっているかを求めたいです．
整数L, M, Nが与えられます．
Lは机の長さ，Mはリボンの数，Nは答えを求める回数です．
M回だけ整数l, rが与えられます．
lはリボンの開始座標，rはリボンの終了座標です．
N回だけ整数pが与えられるので，座標pにリボンは何個重なっているか求めてください．
####制約

\begin{align}
1 \leq L, M, N \leq 100000 \\
1 \leq l \leq r \leq L \\
1 \leq p \leq L \\
\end{align}

####入力例
4 3 1
1 2
2 3
1 4
3
####出力例
2
###考え方
リボンの領域すべてを+1する愚直な方法だと，O(LM)→O(10¹⁰)なのでアウトですね．
累積和を使ってO(M+N)にします．

まず，長さL+2の配列を作り，
リボンの**(開始座標)を+1，(終了座標の1つ右)を-1**します．

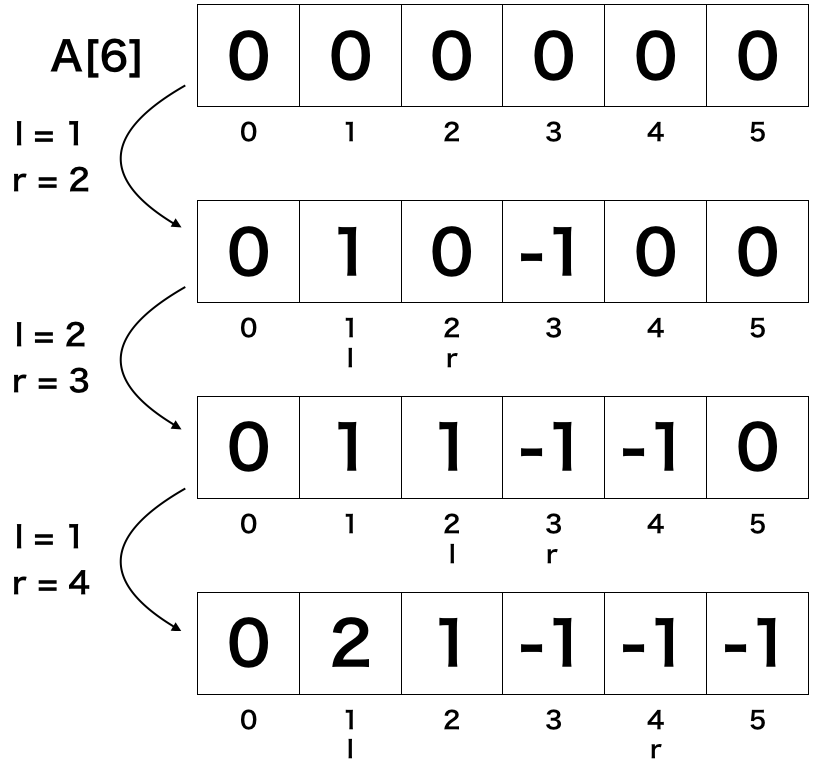
次に，左から右に足していきます．

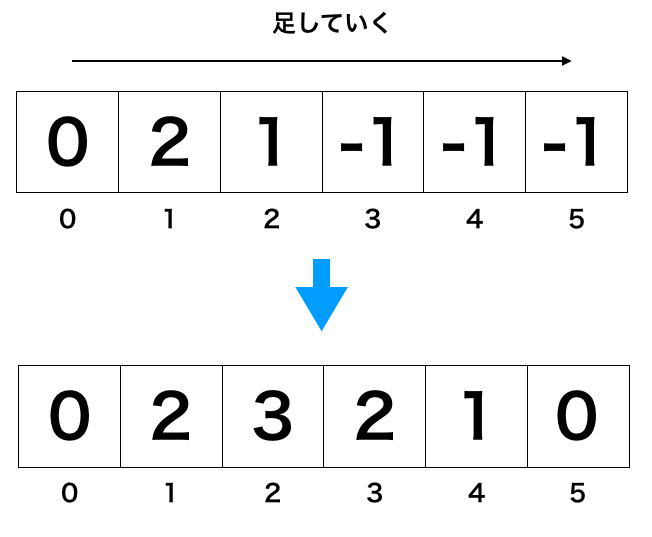
すると各座標のリボンの数が求まります．

###ソースコード

#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
using namespace std;

int main() {
    int L, M, N, l, r, p;
    cin >> L >> M >> N;
    int A[L+2]; rep(i, L+1) A[i] = 0; // init
    rep(i, M) {
        cin >> l >> r;
        A[l]++; A[r+1]--;
    }
    rep(i, L) A[i+1] += A[i];
    rep(i, N) {
        cin >> p;
        cout << A[p] << endl;
    }
    return 0;
}

#おわりに
他にも役立つアルゴリズムは沢山あるので，皆さんも競プロやってみませんか？