Python LightGBMで多クラス分類＆SHAPで予測を解説

概要

LightGBM と　決定木 モデルの精度差は確認しましたが
今度はLightGBMを深堀したいと思います。

サンプルデータ

sample_car_data.csv　（N＝400）

過去に保有車が無い場合：previous_manufacturer 空欄（Nan）

環境

python3.x
jupyter lab

コード

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, ConfusionMatrixDisplay, f1_score
from sklearn.tree import DecisionTreeClassifier, plot_tree
import lightgbm as lgb
import shap

📚サンプルデータを読み込む

#=============================================
# データ読み込む
#=============================================
# CSVファイル(sample_car_data.csv)をShift-JISエンコードで読み込みます。
df = pd.read_csv("L用_sample_car_data_数値.csv", encoding='shift-JIS')
# データの先頭3行を表示して、読み込み結果を確認します
df.head(3)

📨output

📚型の変換

#=============================================
# カテゴリ列のデータをカテゴリ型に変換する
#=============================================
# 数値として扱いたい列（連続値など）
numeric_cols = ["family", "age","children", "income"]

# IDや目的変数は変換対象から除外
exclude_cols = ["customer_id", "manufacturer"]

# 変換対象のカテゴリ列を抽出
categorical_cols = [
    col for col in df.columns
    if col not in exclude_cols + numeric_cols
]

# カテゴリ型にする
df[categorical_cols] = df[categorical_cols].astype("category")

・astype("category")　→　カテゴリ型（category）に変換

数値として扱うべき列を誤ってカテゴリ型に変換しないために、あらかじめ数値として扱いたい列（numeric_cols）や、ID・目的変数（exclude_cols）を除外し、それ以外の列をカテゴリ型に変換しています。

メモリ使用量が減り、処理速度や精度の向上に繋がります。

📚説明変数、目的変数を設定

#=============================================
# 説明変数（特徴量）を設定
#=============================================
# 顧客IDと目的変数の「manufacturer」は除外
X_df = df.drop(['customer_id', 'manufacturer'], axis=1)

#=============================================
# 目的変数を設定
#=============================================
y_df = df['manufacturer']

# クラス数（カテゴリーの種類）を確認
classes = np.unique(y_df)
print("クラス:", classes)

・説明変数（特徴量）　
　→　モデルに入力するデータ。
　→　ここではcustomer_idやmanufacturer（目的変数）は除外。

・目的変数　→　予測したい値で、この例ではmanufacturerがそれにあたる。

・np.unique()　
　→　目的変数のユニークなクラス（カテゴリ）を取得し、分類問題のクラス数を確認。

📨output

📚訓練データとテストデータに分割

#============================================================
# 説明変数(X_df)と目的変数(y_df)を訓練データとテストデータに分割
#============================================================
X_train, X_test, y_train, y_test = train_test_split(X_df, y_df, random_state=0)

print("訓練データ数:", len(X_train))
print("テストデータ数:", len(X_test))

・train_test_split　
　→　モデルの学習に使うデータ（訓練データ）と評価に使うデータ（テストデータ）を分けるための関数。

・random_state　→　固定することで、実行するたびに同じ分割結果を得られる。

・len(X_train)/len(X_test)　
　→　分割後のデータ数を表示して、きちんと分割されているかを確認。

📚 LightGBMによる決定木の学習・予測

#=============================================
# LightGBM：目的に応じて設定
#=============================================
if len(classes) == 2:
    objective = 'binary'
    metric = 'binary_error'
else:
    objective = 'multiclass'
    metric = 'multi_error'

params = {
    'objective': objective,
    'metric': metric,
    'verbose': -1,
}
if objective == 'multiclass':
    params['num_class'] = len(classes)

・if len(classes) == 2　→ クラス数が2なら二値分類（バイナリ分類）として扱う。

・objective = 'binary'　
　→ LightGBMの目的関数（損失関数）を「binary」（2クラス分類用）に指定。
　→ これにより、モデルは2クラス分類用のロジスティック回帰的な処理を行う。

・metric = 'binary_error'
　→　訓練時や検証時の評価指標として「誤分類率（二値分類）」を使う。
　→　精度を測る評価方法の一つ。

else:（つまり、クラスが3つ以上なら）
・objective = 'multiclass'
　→ LightGBMの目的を「多クラス分類」に指定。内部的には softmax を使った分類。

・metric = 'multi_error'　→ 多クラス分類の誤差率を計算する評価指標。

・params['num_class']
　→ 多クラス分類の場合はクラス数を明示的に指定しないとエラーになる。

#=============================================
# LightGBM用データセットを作成（特徴量名を指定）
#=============================================
lgb_train = lgb.Dataset(
    X_train.values,
    label=y_train.values,
    feature_name=X_df.columns.tolist()
)
# モデル学習（50回のブースティング）
lgb_model = lgb.train(params, lgb_train, num_boost_round=50)

#=============================================
# テストデータで予測
#=============================================
y_pred_lgb_prob = lgb_model.predict(X_test.values)
# クラス予測（確率→ラベル）
if objective == 'binary':
    y_pred_lgb = (y_pred_lgb_prob > 0.5).astype(int)
else:
    y_pred_lgb = np.argmax(y_pred_lgb_prob, axis=1)
# ==============================
# SHAP値計算
# ==============================
explainer = shap.Explainer(lgb_model, X_df)
shap_values = explainer(X_df)
print("SHAP values shape:", shap_values.values.shape)

・lgb.Dataset(...)　→　LightGBM 専用のデータ構造に変換

・X_train.values　→　NumPy配列に変換した訓練データの特徴量。

・label=y_train.values　→　目的変数（正解ラベル）。

・feature_name　
　→ 特徴量名を明示的に渡すことで、可視化や特徴量重要度の出力時に列名がそのまま使われる。
　→ 渡さないと「feature_0, feature_1,…」のように自動生成されるので注意

・X_df.columns.tolist()　→　元の特徴量名をリストで渡す。

・predict()　
　→ 出力はクラスごとの確率なので、2値分類と多クラス分類で後処理を分る

・shap.Explainer → LightGBMモデルに適したSHAP計算器を自動で選択して作成。
・shap_values → 中身は、各サンプルごと・各特徴量ごとの「予測への寄与度」。
・shap_values = explainer(X_df)
　→ 1件ずつ、「どの特徴量が、どのくらい予測に影響したか（+/-）」を出力。

❓SHAP値とは

特徴量ごとの影響力を数値化したもの

正の値 → その特徴量が「予測クラスを選ぶ方向にプラスに作用」した
負の値 → その特徴量が「予測クラスを選ぶ方向にマイナスに作用」した

📚 モデルの評価

#=============================================
# 精度評価
#=============================================
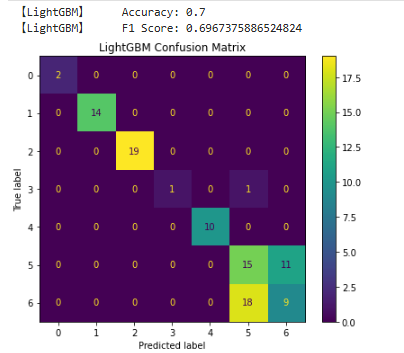
print("【LightGBM】     Accuracy:", accuracy_score(y_test, y_pred_lgb))
print("【LightGBM】     F1 Score:", f1_score(y_test, y_pred_lgb, average='weighted'))

#=============================================
# 混同行列の表示
#=============================================
fig, ax = plt.subplots(figsize=(6, 5))

ConfusionMatrixDisplay.from_predictions(y_test, y_pred_lgb, ax=ax)
ax.set_title("LightGBM Confusion Matrix")

plt.tight_layout()
plt.show()

📨output

📌Accuracy（正解率）: 0.7
意味：全予測のうち 70% が正解 だった。
解釈：一般的な基準で見れば「そこそこの性能」だが、クラスの不均衡がある場合は過大評価されることもあり。

📌F1 Score（加重平均）: 0.6967...
意味：Precision（適合率）と Recall（再現率）のバランスを取った指標。
average='weighted' によって、各クラスのF1スコアをサンプル数で重みづけして平均しています。

Accuracy（0.70）とF1スコアが近い値になっていることから、PrecisionとRecallのバランスは比較的取れていると考えられる。
ただし、いずれも0.7弱という結果なので、性能はまずまずだが、さらなる改善の余地あり。

つまり　サンプルデータだから仕方なし

📚 特徴量重要度の可視化

#=============================================
# LightGBMの特徴量重要度 (特徴量名表示)
#=============================================
ax = lgb.plot_importance(
    lgb_model,
    max_num_features=10
)
plt.title("LightGBM Feature Importance")

plt.savefig("比較用_LightGBM_Feature.png", dpi=300)

・lgb.plot_importance()　
　→　 LightGBM が持つモデル（lgb_model）の 特徴量重要度をグラフ化する関数。

・max_num_features=10　→　重要度の高い上位10個の特徴量だけを表示する指定。

📨output

📌Y軸 →　income, age, region … → 特徴量名
📌X軸 →　それぞれの「重要度」（数値）　→ 値が大きいほど、モデルがその特徴量をより重視している

特徴量（feature）は、モデルに入力される説明変数のことで、
目的変数（予測したい値）ではありません。

🔎 特徴量重要度とは？
特徴量重要度は、モデルが学習中に「どの特徴量をどれだけ使ったか」や「どれだけ影響力があるか」を数値化したもの。
LightGBMの場合、デフォルトの重要度は「分割に使われた回数（split count）」や「情報利得の合計」などが使われます。
重要度が高い特徴量ほど、モデルの予測に大きく貢献しています。

❓なぜX軸が400件を超えて大きくなるの？
それは「特徴量重要度の計算方法」に理由があるからです。

LightGBM の plot_importance() の デフォルト設定（importance_type='split'） では、各特徴量が分岐に使われた回数をカウントしています。

重要度のカウントの仕組み（importance_type='split'）

• 1本の決定木には複数の分岐（ノード）がある。
• LightGBMは複数本の木（例：100本）を学習する。
• 各木で説明変数が分岐の条件として使われるたびにカウントされる。
• 1つの特徴量が何十回、何百回も使われることがある。
• その合計回数が「Feature Importance」としてX軸に表示される。

例）
・データ数：400件 （400件のデータに対して）
・木の本数：100本 （100本の決定木を作ったモデルの中で）
・「income」という特徴量が分岐条件として使われた回数が合計で 2507回 ある。

📚 多クラス分類モデルの構築と予測

# ==============================
# LightGBMパラメータ設定
# ==============================
params = {
    'objective': 'multiclass',
    'metric': 'multi_error',
    'num_class': len(classes),
    'verbose': -1
}

# ==============================
# 学習（100回で学習）
# ==============================
lgb_model = lgb.train(params, lgb_train, num_boost_round=100)

# ==============================
#  全データに対する予測
# ==============================
y_all_pred_prob = lgb_model.predict(X_df.values)  # 予測確率
y_all_pred = np.argmax(y_all_pred_prob, axis=1)  # 予測クラスラベル

・lgb.train(...)
　→ LightGBMモデルを学習させる関数。
　→ 指定したパラメータとデータに基づいて、ブースティングによるモデル構築を行う。

・params
　→ LightGBMのパラメータを辞書形式で設定（例：目的関数や評価指標など）。

・lgb_train：　→ 訓練用データセット。lgb.Dataset で作成された LightGBM専用の形式。

・num_boost_round=100 →　100回のブースティング（決定木を100本） で学習。

・lgb_model.predict(...)
　→ 全データ（X_df）に対して予測を実行。
　→ 出力は各クラスに属する確率の配列（shape = (サンプル数, クラス数)）。。

・np.argmax(..., axis=1)
　→ 各サンプルについて、**最も確率が高いクラスのインデックス（=予測ラベル）を取得。
　→ これが最終的なクラス予測（y_all_pred）となる。
・predict() →　モデルによる予測結果を返す。出力は「クラスごとの確率」。

❓2値分類（binary classification）：
出力（目的変数）が 2つのクラス のいずれかに分類される「問題（problem）
例）Yes / No、True / False、スパム / 非スパム、購入する / 購入しない

❓多クラス分類（multi-class classification）：
出力が 3つ以上のクラス に分類される「問題（problem）
例）トヨタ / ホンダ / 日産、A / B / C / D（テスト評価）、動物分類

🔍どちらも「分類問題（classification）」の一種で、
　違いはクラスの数（2つか、3つ以上か) です。

💡ちなみに
・クラスが2つ：binary
・クラスが3つ以上：multi-class
・複数ラベルを同時に扱う：multi-label（また別の概念）

📚 上位3候補の抽出

# ==============================
# 上位3候補の抽出
# ==============================
top3_classes = np.argsort(y_all_pred_prob, axis=1)[:, ::-1][:, :3]
top3_probs = np.sort(y_all_pred_prob, axis=1)[:, ::-1][:, :3]

・np.argsort()
　→　各サンプルに対する全クラスの確率をソートし、上位3つのクラス（とその確率）を取得。
・top3_classes → 上位3つのクラスのインデックス（＝予測ラベル）を格納。
・top3_probs → それぞれのクラスの予測確率を格納。

この処理によって、各サンプルごとに「予測の上位候補リスト（第1〜3位）」を取得できます。

📚 元データに結果を追加

# ==============================
# 元データに結果を追加
# ==============================
df["predicted_manufacturer"] = y_all_pred

for i in range(y_all_pred_prob.shape[1]):
    df[f"prob_class_{i}"] = y_all_pred_prob[:, i]

# 上位3クラスと確率の列を追加
for i in range(3):
    df[f"top{i+1}_class"] = top3_classes[:, i]
    df[f"top{i+1}_prob"] = top3_probs[:, i]
    
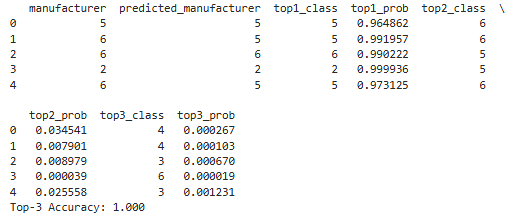
print(df[[
    "manufacturer",               # 正解ラベル
    "predicted_manufacturer",     # モデルの予測
    "top1_class", "top1_prob",    # 1位予測と確率
    "top2_class", "top2_prob",    # 2位予測と確率
    "top3_class", "top3_prob"     # 3位予測と確率
]].head())

・df["predicted_manufacturer"] = y_all_pred
→ LightGBMモデルの予測結果（最も確率が高かったクラス）を、元のデータフレームに追加。
（これは最終的な「1位予測（予測ラベル）」です。分類問題で最もよく使う結果。）

・for i in range(y_all_pred_prob.shape[1]):
→ クラス数（n_classes）だけループして、それぞれのクラスについて「予測確率」を列として追加。（prob_class_0, prob_class_1, ...）
→ 各クラスにどの程度自信を持って予測しているかが分かる。
→ 分析や可視化（例：確率ヒストグラムや誤予測の分析）で非常に役立つ。

・dftop{i+1}_class → 予測確率が高い順に並べた上位3クラスのインデックス（ラベル）

・top{i+1}_prob → そのクラスの予測確率

📚 Top-3 Accuracy（上位3クラスに正解が含まれている割合）

# =======================================
# 　正解割合（Top-3 Accuracy）
# =======================================
top3_accuracy = np.mean([
    y_true in top3 for y_true, top3 in zip(df["manufacturer"], top3_classes)
])
print(f"Top-3 Accuracy: {top3_accuracy:.3f}")

・df["manufacturer"] →　 各サンプルの 正解ラベル（目的変数）

・top3_classes
　→　モデルが出力した 上位3クラスのインデックス（shape = [n_samples, 3]）

・zip(df["manufacturer"], top3_classes)
　→　各サンプルについて (正解ラベル, 上位3クラス) を1組にまとめる

・y_true in top3 →　正解ラベル y_true が top3 の中に含まれているかを判定（True / False）

・np.mean([...]) →　True=1, False=0 として平均を取る → Top-3 Accuracy（割合） を計算

manufacturer（正解）	top3_classes（予測上位3）	判定 y_true in top
5	[5, 2, 1]	True
3	[5, 3, 2]	True
6	[1, 2, 4]	❌False

このコードでは、モデルの予測候補（上位3クラス）の中に正解ラベルが含まれていた割合、つまり Top-3 Accuracy を計算しています。

これは「1位は外したが、2位または3位には正解が含まれていたか？」を評価する指標で、多クラス分類や推薦システム、診断支援などの実務で非常に有用な評価軸です。

❓Top-3 Accuracy を見る意義って
多クラス分類では、
1位の予測が外れても「候補リストに正解が含まれていたか」 が重要。

特に実務（例：商品推薦、検索候補、診断支援）では、Top-1 精度よりも
Top-N 精度の方が重要視されるケースが多い。

📨output

📌manufacturer →　正解ラベル（実際のクラス）
📌predicted_manufacturer →　モデルが予測したクラス（＝ top1_class と同じ）
📌top1_class, top1_prob →　最も確率が高かったクラスとその確率
📌top2_class, top2_prob →　2番目に確率が高かったクラスとその確率
📌top3_class, top3_prob →　3番目に確率が高かったクラスとその確率

例）1行目：
正解: manufacturer = 5
予測: predicted_manufacturer = 5（＝ top1_class）
確率: top1_prob = 0.96（高信頼）
top3: [5, 6, 4] → 全体の予測候補（降順）

モデルの信頼度（確率）も高く、top1_prob > 0.95 のサンプルが多いため、予測に強い自信を持ってますね。

「正解が top3 に入っているかどうか」を見る評価指標は、特に候補提示型システム・レコメンド・診断系タスクで重要な視点です。

❓Top-3 Accuracy: 1.000

これは「全てのサンプルで、正解ラベルが top3 のどれかに含まれていた」ということで、非常に高い補助的精度（= Top-3 Accuracy）です。

特に多クラス分類（例えば今回のクラス数は6など）では、「1位は外したけど、top3には入ってた」というケースはよくあります。

実務でも推薦システムや選択肢提示型のタスクでは、Top-3 精度が重要な指標になります。

📚 Top-N の中で正解が「何位」だったかを確認

各サンプルごとに、正解ラベル（manufacturer）が top3 に含まれているか。
含まれているなら、それは1位・2位・3位のうち何番目だったか？ を調べます。

# =======================================
# 正解が topN の何番目
# =======================================
def top_rank(row):
    true_class = row["manufacturer"]
    top_classes = [row["top1_class"], row["top2_class"], row["top3_class"]]
    return top_classes.index(true_class) + 1 if true_class in top_classes else None

df["correct_rank"] = df.apply(top_rank, axis=1)
print(df["correct_rank"].value_counts())

・true_class →　正解ラベル（例：manufacturer列）
・top_classes →　モデルの予測した top1〜top3 のクラス
・index(true_class) →　正解が top1〜3 の何番目に出てくるか（0,1,2）を取得
・+1 →　ランク（順位）として使いたいので、0-based を 1-based に直す
・if true_class in top_classes →　正解が top3 に含まれていない場合は None を返す

📨output

correct_rank 列に正解クラスが予測の上位何位に入っていたかを示す。

📌1 → 370件 → 正解が top1（最上位予測）だったサンプル数
📌2 → 30件 → 正解が top2（2番目に高い確率）だったサンプル数
📌3/None なし（ゼロ件） → 正解が top3に含まれていない

🎯 解説

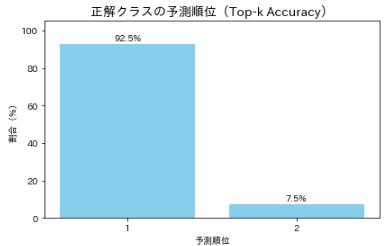
・正解が1位：92.5%（370 / 400）
　→ 予測が的中。自信を持って正解を当てている

・正解が2位：7.5%（30 / 400）
　→ 惜しい予測。迷ったが正解は含まれている

・3位以下・圏外：0件
　→ 正解がtop3外に出ることはなかった → 安心感あり

モデルの予測精度は非常に高く、正解が上位候補に含まれています。
単純な accuracy（正解率）ではなく、「Top-N 内に正解が含まれているか」を評価することで、レコメンドや診断支援など、複数候補を提示するタイプの応用に適したモデル かどうかを判断できます。

また、Top-1を外した場合でも、Top-2に正解が含まれるケースが多く選択肢の提示や候補提案を行う実務においても、信頼性の高い予測 といえるでしょう（たぶん）。

特に、診断支援や製品推薦のようにTop-k 精度が重要視されるシナリオでは、正解がTop-2以内に含まれていることはモデルが迷いつつも適切な候補を挙げていることの証拠といえます（ホントか）。

※❓Top-k 精度（Top-k accuracy）
　→ 予測上位k個のうち、少なくとも1つが正解である確率。

📚 正解の順位別の件数・割合を可視化する（参考程度）

# =======================================
#正解の順位別の件数・割合を可視化
# =======================================
import matplotlib.pyplot as plt
import japanize_matplotlib  # 日本語対応

rank_counts = df["correct_rank"].value_counts().sort_index()
rank_percent = (rank_counts / rank_counts.sum()) * 100

fig, ax = plt.subplots(figsize=(6, 4))
bars = ax.bar(rank_percent.index.astype(str), rank_percent.values, color='skyblue')

for bar in bars:
    height = bar.get_height()
    ax.text(bar.get_x() + bar.get_width()/2, height + 1,
            f"{height:.1f}%", ha='center', va='bottom')

ax.set_title("正解クラスの予測順位（Top-k Accuracy）", fontsize=14)
ax.set_xlabel("予測順位")
ax.set_ylabel("割合（%）")
plt.ylim(0, 105)
plt.tight_layout()
plt.show()

📨output

📚 各サンプルごとに、予測結果に最も影響を与えた上位3つの特徴量（SHAP値）を抽出

shap_values（SHAPによる特徴量重要度）を使って、
「この予測には、どの特徴量が最も影響したか？」 を各サンプル単位で記録。
→ モデルの「予測理由」を明らかにする分析です。

# ==============================
# 上位3寄与特徴量抽出
# ==============================
results_top3 = []

for i in range(len(df)):
    pred_class = df.loc[i, "predicted_manufacturer"]
    shap_vals = shap_values.values[i, :].flatten()
    features = list(shap_values.feature_names)

    # 絶対値で上位3特徴量を選ぶ
    top_idx = np.argsort(np.abs(shap_vals))[::-1][:3]
    top_features = [features[j] for j in top_idx]
    top_values = [shap_vals[j] for j in top_idx]

    tmp = {
        "customer_id": df.loc[i, "customer_id"],
        "predicted_class": pred_class,
        "top1_feature": top_features[0],
        "top1_value": top_values[0],
        "top2_feature": top_features[1],
        "top2_value": top_values[1],
        "top3_feature": top_features[2],
        "top3_value": top_values[2]
    }
    results_top3.append(tmp)

top3_df = pd.DataFrame(results_top3)
top3_df.head(3)

・for i in range(len(df)):
→ 各サンプル（顧客など）ごとに処理を行います。全件ループ。

・pred_class = df.loc[i, "predicted_manufacturer"]**
→ そのサンプルに対してモデルが予測した クラス（ラベル） を取得。

・shap_vals = shap_values.values[i, :].flatten()
→ そのサンプルに対する SHAP値（= 各特徴量の貢献度） を取得。flatten()で1次元配列に。

・SHAP値が正 → その特徴が予測を 押し上げた

・SHAP値が負 → その特徴が予測を 押し下げた

・features = list(shap_values.feature_names)
→ 特徴量名のリストを取得（例：["age", "income", "gender", ...]）

・ top_idx = np.argsort(np.abs(shap_vals))[::-1][:3]
→ 絶対値が大きい（＝影響が強い）順に上位3特徴量のインデックスを取得

・np.abs(...)： → 正負関係なく「どれだけ影響したか」

・[::-1]： → 降順ソート（大きい順）。SHAP値は正負を持つが、どちらでも“強く影響した”特徴量を拾いたいため、絶対値で比較する。

・[:3]： → 先頭3つを抽出（＝Top3）
・top_features = / top_values= → 上で得たインデックスに基づいて、実際の特徴名と SHAP値 を取得。

・tmp = {} → 各サンプルごとに「どの特徴が、どのくらい予測に貢献したか」を辞書で保存。
・results_top3.append(tmp) → 全サンプル分の記録をリストに蓄積。

・top3_df = → 各行が「1サンプルごとのTop3影響特徴量」の一覧になります。

📨output

📌customer_id]： → 1（顧客ID＝1）
📌predicted_class]： → 5（モデルはクラス「5」を予測）
📌top1_feature]： → car_preference（「好きなボディタイプ」が予測に最も影響）
📌top1_value]： → -2.708841 （この特徴量はクラス「5」への影響を強くマイナス方向に与えた＝押し下げ）
📌top2_feature]： → income（次に影響の強い特徴量は「収入」）
📌top2_value 1.777839]： → 1.777839（収入はプラスに働き、クラス「5」予測を押し上げた）
📌top3_feature]： → age（3番目に影響力のある特徴量は「年齢」）
📌top3_value -1.391056]： → -1.391056（年齢はマイナスに作用している）

❓SHAPの何が良いの

🎯各ユーザーやサンプルごとにどの特徴量がどれくらい予測に影響したかを数値で可視化できる
　→ 例えばなぜこの顧客にクラス5を予測したのか？ を定量的に説明可能。
　(個々の予測に対して、なぜそうなったのかがわかる）

🎯特徴量ごとのプラス・マイナスの寄与度が明示される
　→ モデルの判断理由が明確に見える
　→ モデルの透明性・信頼性が向上する　（他の手法よりも一貫性と理論的正しさがある）

🎯医療・金融・レコメンドなど
　'なぜその予測になったか'を説明しなければならない領域 で特に重要
　→ （SHAPで）説明責任を果たせる
　→ モデル全体でどの特徴量が重要かも確認できる（グローバルな解釈も可能）

🎯重要ユーザーの要因分析や予測の根拠を社内・クライアント向けに説得力をもって提示可能。

📚 データマージ

# ==============================
# マージ用に列名を合わせる
# ==============================
df = df.rename(columns={"predicted_manufacturer": "predicted_class"})
# ==============================
# マージ
# ==============================
df_merged = pd.merge(df, top3_df, on=["customer_id", "predicted_class"], how="left")

dfには predicted_manufacturer という列があるが、top3_df には同じ情報が predicted_class という列名で入っている。
そのため、マージのために列名を揃える（統一しないと merge できない）。

📚 列名リネーム（お好みで）

# ==============================
# 列名リネーム　		
# ==============================
rename_dict = {
    "top1_feature": "上位1特徴量",
    "top1_value": "上位1寄与度",
    "top2_feature": "上位2特徴量",
    "top2_value": "上位2寄与度",
    "top3_feature": "上位3特徴量",
    "top3_value": "上位3寄与度",
    "prob_class_0": "メーカー0の確率",
    "prob_class_1": "メーカー1の確率",
    "prob_class_2": "メーカー2の確率",
    "prob_class_3": "メーカー3の確率",
    "prob_class_4": "メーカー4の確率",
    "prob_class_5": "メーカー5の確率",
    "prob_class_6": "メーカー6の確率",
    "top1_class": "トップ1候補メーカー",
    "top1_prob": "トップ1確率",
    "top2_class": "トップ2候補メーカー",
    "top2_prob": "トップ2確率",
    "top3_class": "トップ3候補メーカー",
    "top3_prob": "トップ3確率"
}
df_merged = df_merged.rename(columns=rename_dict)

・rename_dict → リネームの設定（辞書）を作る

・df_merged.rename(columns=rename_dict)
　→ 実際にDataFrameの列名を辞書に従って変更する

📚 CSVに出力

# ==============================
# CSV出力
# ==============================
df_merged.to_csv("predictions_with_top3.csv", index=False, encoding="utf-8-sig")

#=============================================
#　Topデレクトリとリストファイルを開く
#=============================================
import os
import os.path as osp
current_dpath = os.getcwd()

os.startfile(current_dpath)
os.startfile(current_dpath + "\\predictions_with_top3.csv")

print(" 完了")

📚 出力されたファイル内容

📌N列：現在の保有メーカ＝正解ラベル
📌O列：予測されたメーカ
📌 P列〜Y列（確率）：各メーカごとの予測確率
　メーカー0の確率（例：0.0123 → 1.23%）
　メーカー1の確率...prob_class_6 → メーカー6の確率
📌 W列〜AB列（Top候補）：確率上位3位までの予測クラスとその確率
　トップ1メーカー、トップ1確率 → 最も確率の高いメーカーとその確率
　トップ2メーカー、トップ2確率 → 2番目に確率の高いメーカーとその確率
　トップ3メーカー、トップ3確率 → 3番目に確率の高いメーカーとその確率
📌 AC列（正解のランク）：正解メーカがTop何位に含まれていたか。
　例：1ならTop1、2ならTop2
　correct_rank = 1 → 正解がTop1に入っていた（予測と一致）
　correct_rank = 2 → 正解がTop2にいた（ニアミス）
　correct_rank = 3 → 正解がTop3にいた（惜しい）
　correct_rank = np.nan → Top3に正解が含まれていない（はずれ）

📌AD列、AF列、AH列：上位1、２，３位の特徴量（説明変数）
📌AE列、AG列、AJ列：上位1、２，３の寄与率

❓何を意味してるの
その人が予測のモデルを選ぶのに影響する上位3位って事

🔍1行目のケースで説明します

✅ car_preference（車のボディタイプ）が最も影響力があり、値は -1.397
　→ その車のボディタイプが好みではない（＝マイナスに働く）
　→ 本来なら そのメーカーは選ばれにくい はずだった。

✅ ・age（年齢）は2番目に影響し、マイナス寄与
　→ この年齢層は そのメーカーを選びにくい傾向にある。
　→ 年齢的な嗜好やライフステージが合わない可能性がある

✅ income（収入）は3番目に影響し、正の値 0.808
　→ 収入によって、そのメーカーを選べる／選びたい要素が強まった。
　→ 車の価格帯・ブランド価値とのマッチが想定される

💮 結論：
この人は予測で「メーカー5」になったが、
実はcar_preferenceやageの影響で本来そのメーカーは選ばれにくい。
しかし、income（収入）がプラスの影響を与えたので最終的にそのメーカーが予測された。

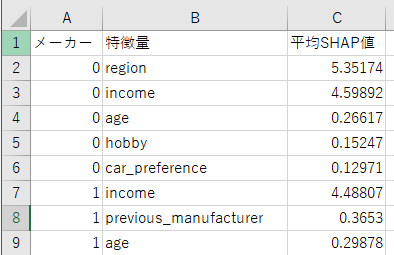
📚 参考：メーカー毎の特徴量重要度ランクを出す

各「予測されたメーカー」ごとに、SHAP値の平均を使って「特徴量の重要度ランキング」が出力されます

# SHAP値と特徴量名をDataFrameに変換
shap_df = pd.DataFrame(shap_values.values, columns=X_df.columns)
shap_df["predicted_class"] = df["predicted_class"].values  # 予測されたクラスを結合



# クラスごとの SHAP値の平均（特徴量別）を求める
summary_list = []

for cls in sorted(df["predicted_class"].unique()):
    shap_mean = shap_df[shap_df["predicted_class"] == cls].drop(columns="predicted_class").mean().abs()
    shap_mean_sorted = shap_mean.sort_values(ascending=False)

    for feature, value in shap_mean_sorted.items():
        summary_list.append({
            "メーカー": cls,
            "特徴量": feature,
            "平均SHAP値": round(value, 5)
        })

# DataFrameとしてまとめる
shap_summary_df = pd.DataFrame(summary_list)

# メーカーごとに上位5個を表示（必要なら変更可能）
topN = 5
display_df = shap_summary_df.groupby("メーカー").head(topN)


# CSV保存
display_df.to_csv("メーカー別_SHAP_特徴ランキング.csv", index=False, encoding="utf-8-sig")

❓何を意味するの？
　→「メーカーごとの重要な特徴量」がわかります。

📌メーカー列（0, 1, ...） →　予測対象のクラス（車メーカーの種類 0～6）。
📌特徴量列 →　予測に使われた説明変数（age, incomeなど）。
📌平均SHAP値
→　「その特徴量が、どれだけそのメーカーの予測に寄与したか」の平均（※絶対値ベース）。
→ 値が大きいほど、その特徴量が予測に強く関与したことを示す

🔍説明します
🎯メーカー0の予測
・予測に強く影響している特徴量は「region（居住地）」と「income（収入）」
・特に「region（居住地）」が5.35で最も大きく影響
・「age（年齢）」や「hobby（趣味）」の影響は小さい
🎯メーカー1の予測
・「income（収入）」が一番強い影響　（他略）

🔍結論
💮メーカー0の購入者層
→　居住地や収入によって購入が強く左右されている。
→　年齢や趣味の影響は小さい。
→　地域別のマーケティングや所得層に合った商品企画が重要

💮メーカー1の購入者層
→　収入の影響が大きい。
→　高収入層向けの広告や販売戦略に力を入れるべき

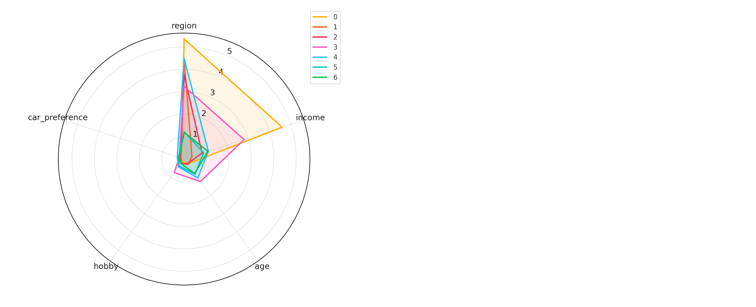
レーダーにするとこんな感じで居住地、世帯収入に偏ってますね
まあ、サンプルデータなんで

まとめ

この分析をしながら
　📌クラスタリングして
　📌セグメント名を付けて
　📌それぞれに近いデモグラの人に同様のアプローチをする
とビジネスに使えるかな？と思いました。

💰例えば

セグメント名	特徴	施策例
20代SUV好き層	20代、SUV、SHAPでcar_preference強	若者向けSUV新モデルのDM送付、SNS広告
高収入×セダン志向	高収入、セダン、SHAPでincomeが強く正方向	高級感あるセダンを訴求、ローンシミュレーション提案
ファミリー層（ミニバン好き）	同居家族多、子どもあり、ミニバン	チャイルドシート搭載可能な車紹介、家族割引訴求

購入予測する場合は、もっと細かい説明変数のデータが必要です。
機会があれば投稿します。