対象読者
- ディープラーニングの概要をある程度把握している方
- 活性化関数がなぜ必要なのか分からない方
- 雑な説明でも許せる方
問題
活性化関数はディープラーニングの重要な要素の一つです．
ですが何故必要なのでしょうか？
- 複雑にしたいなら層を増やせば良いだけなのでは？
- なぜ非線形関数である必要があるの？
などの疑問が湧くと思います．
そんな疑問を一緒に紐解いていきましょう!
解説
まず1層の場合を見てみましょう
入力を$x$，重みを$w$，バイアスを$b$とすると，層は
$xw+b$と表せます．
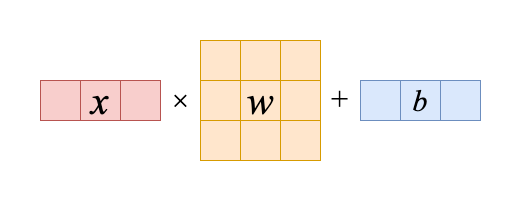
簡単ですね．
次に2層の場合を見てみましょう
$w_1$は1層目の重み，$w_2$は2層目の重みです．
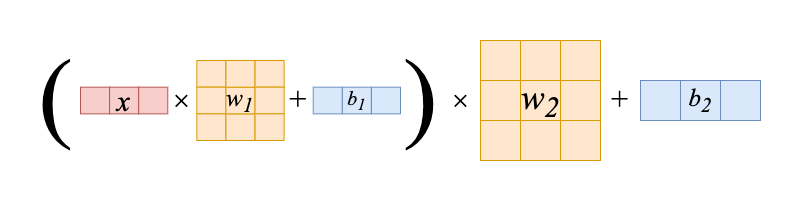
式は $(xw_1+b_1)w_2+b_2$ となります．
1層目の出力を2層目に入れただけです．
簡単ですね.
本題
上の2層の場合を変形していきます．
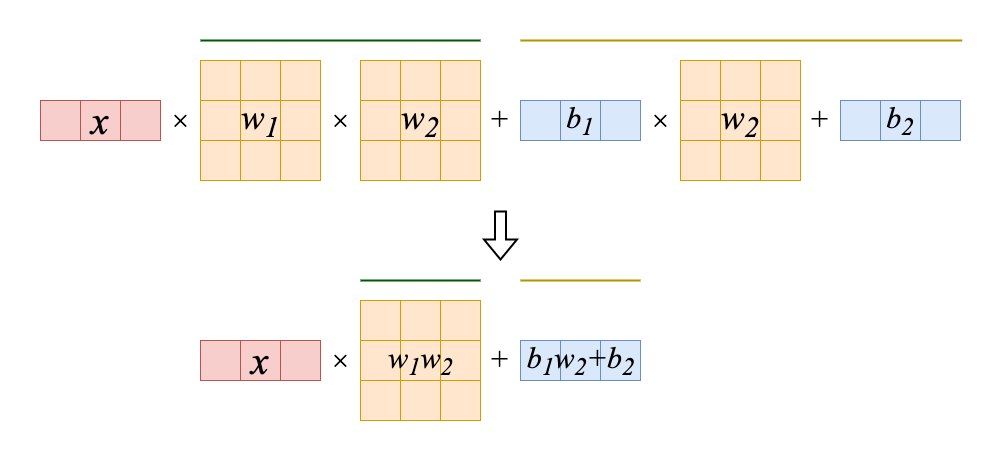
線形代数の分配法則から次のように展開できます．
$w_2$を赤と青の部分にそれぞれ掛けていきます．
次に結合法則から黄色と緑の部分を先に計算してしまいます．
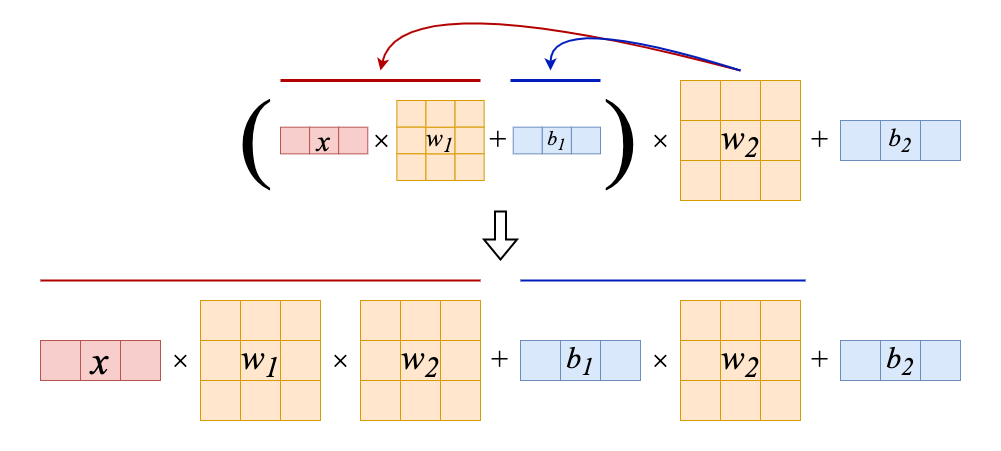
どうでしょうか，
2層の複雑な図が1層のようにスッキリと表すことができました．
気持ちいいですね！
気持ちいいまま止まっていてはいけません．
ここでスッキリした図をよくみてみましょう.
1層の時と同じ形ですね.
つまり，活性化関数がない場合どんなに層を深くしても1層と同じ式に変形できてしまうのです．
これで層を深くしても活性化関数がなければ複雑にならないことがわかりましたね.
では活性化関数を使った場合はどうでしょうか？
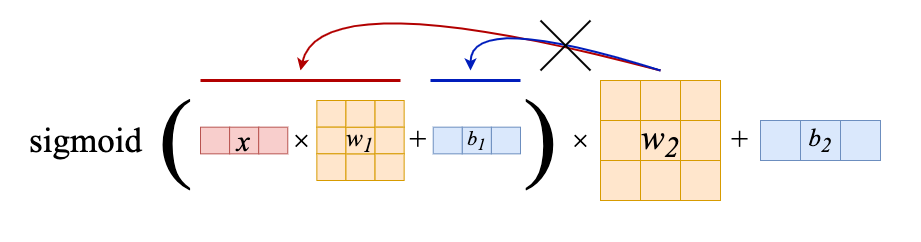
活性化関数を使った場合
はい，こんな感じです．展開できずスッキリしませんね．
ここで重要なのは活性化関数が非線形な点です．
線形だと展開できてしまいますからね．
これで活性化関数が非線形である必要がわかりましたね．
終わりに
自分自身勉強し始めた際ここで躓いて苦労しました．
誰かの支えになれたら幸いです．
訂正などがありましたら遠慮なく言ってください．私が成長できます．