はじめに
最近、決定木とNeural Networkを融合した研究をちょくちょく見かけます。
その多くが、2つの手法を融合することで、決定木のわかりやすさとNeural Networkの表現力の高さを両立させることを目指しています。
今回はその中でも最近発表された、End-to-end Learning of Deterministic Decision Trees という論文の手法を実装したので紹介してみたいと思います。
アルゴリズムの実装および実験で使用したコードは僕のgithubに上げてあります。
決定木の確率モデル
以下、分類問題を想定します。この論文では決定木の各ノードの分岐関数にNeural Networkを用います。
各Neural Networkはそのノードにたどり着いたデータを入力とし、決定木を右に進むか、左に進むかという確率値を出力します。各リーフにはそのリーフに辿りついたデータのクラス分布を表す実数値のベクトルが割り当てられます。
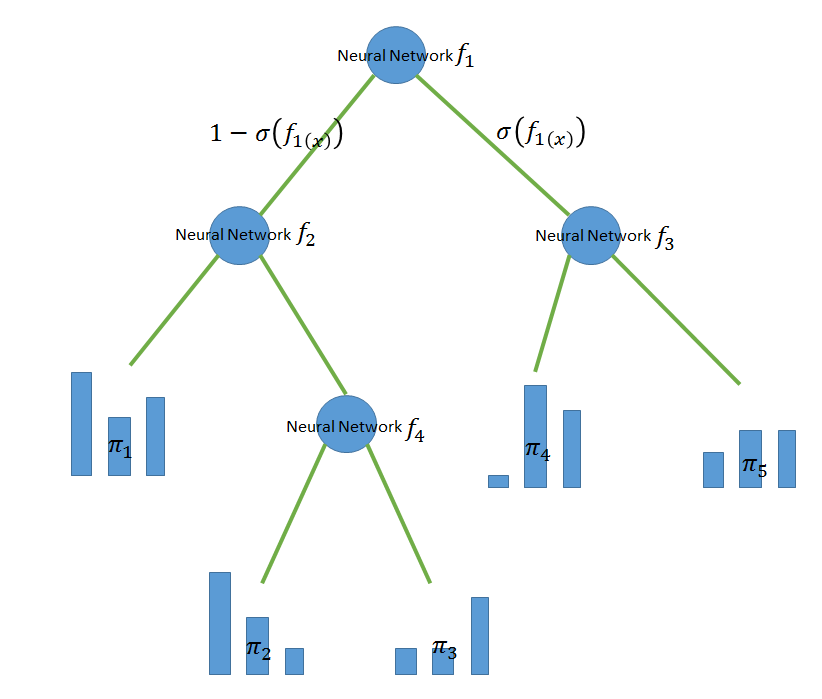
このモデルを次のように定式化します。
まず、
\begin{align}
K&: クラス数 \\
l \in \bigl\{ 1,...,L \bigr\} &:リーフ \\
\pi_l&: リーフ\hspace{0.5mm}lに付随する分布 \hspace{1cm} \sum_{k=1}^{K}(\pi_l)_k = 1 \\
f_a()&: ノード \hspace{0.5mm}aに付随するNeural Networkが表す関数 \\
R_l&: リーフ\hspace{0.5mm}l にたどり着くために右に進んだノード群 \\
L_l&: リーフ\hspace{0.5mm}l にたどり着くために左に進んだノード群 \\
\end{align}
とします。このとき入力$x$がリーフ$l$にたどり着く確率$\mu_l(x)$は
$$\mu_l(x)=\prod_{r \in R_l}\sigma(f_r(x))\prod_{l \in L_l}(1-\sigma(f_l(x)))$$
となります。
これを利用して入力$x$がラベル$y$となる確率は
$$p(y|x)=\sum_{l=1}^{L}(\pi_l)_y\mu_l(x)$$
となります。
学習時はこのようにすべてのリーフを利用した予測を行いますが、推論時は計算時間の削減や解釈可能性を高めるため、通常の決定木と同じようにルートノードから順にNeural Netを実行して進むノードを決めていき、たどり着いた1つのリーフのみを使用して予測を行います。このとき予測分布はたどり着いたリーフの$\pi$になります。
目的関数と最適化
目的関数
決定木の構造は固定して、各ノードのNeural Netのパラメータ、および各リーフに対応する$\pi_l$を最適化することを考えます。(論文では木構造の学習にも言及されていますが、今回は省略します。)
上記の$p(y|x)$を利用して、最尤法+SGDで最適化してもよいのですが、[1]ではデータ$x_n$がリーフ$l$にたどり着くかどうか(1or0)という潜在変数$z_{n,l}$を導入し、尤度関数を次のように定義します。
$$L(\theta, X, Y, Z)=\sum_{n=1}^{N}\sum_{l=1}^{L}z_{n,l}log((\pi_l)_{y_n}\mu_l(x_n;\theta))$$
($\theta, X, Y, Z$はそれぞれモデルパラメータ、入力データ、ラベルデータ、潜在変数の集合を表します。)
最適化
[1]では上記の尤度関数をEMアルゴリズムで最適化しています。k-meansのアルゴリズムでいうと、上記潜在変数$z_{n,l}$が各データがどのクラスタに属するかという変数に対応します。
E-step
$\theta_{t-1}$ を固定したとき潜在変数の分布上で尤度関数の期待値$Q(\theta_t|\theta_{t-1})=E_{Z|X,Y,\theta_{t-1}}[L(\theta_t, X, Y, Z)]$をとります。これには尤度関数内の$z_{n,l}$をその期待値$h_{n,l}$に変換すればよく、
Q(\theta_t|\theta_{t-1})=\sum_{n=1}^{N}\sum_{l=1}^{L}h_{n,l}log((\pi_{l,t})_{y_n}\mu_l(x_n,\theta_{t}))
となります。潜在変数の期待値は次のように計算できます。
\begin{align}
h_{n,l}&=p(z_{n,l}=1|x_n,y_n,\theta_{t-1}) \\
&= \frac{p(y_n|z_{n,l}=1,x_n,\theta_{t-1})p(z_{n,l}=1|x_n, \theta_{t-1})}{p(y_n|x_n,\theta_{t-1})} \\
&= \frac{(\pi_{l,t-1})_{y_n}\mu_l(x_n,\theta_{t-1})}{\sum_{m=1}^{L}(\pi_{m,t-1})_{y_n}\mu_l(x_n,\theta_{t-1})}
\end{align}
M-step
$Q(\theta_t|\theta_{t-1})$ を$\theta_t$に関して最大化します。
Q(\theta_t|\theta_{t-1})=\sum_{n=1}^{N}\sum_{l=1}^{L}h_{n,l}log((\pi_{l,t})_{y_n})
+ \sum_{n=1}^{N}\sum_{l=1}^{L}h_{n,l}log(\mu_l(x_n,\theta_{t}))
と、$\pi$とNeural Netの部分が完全に分離でき、$\pi$に関しては次のような解析解が得られます。
(\pi_{l,t})_{k}=\frac{\sum_{n=1}^{N}\delta(y_n=k)h_{n,l}}{\sum_{n=1}^{N}h_{n,l}}
のこるNeural Netに関する部分は
$$\sum_{n=1}^{N}\sum_{l=1}^{L}h_{n,l}log(\mu_l(x_n,\theta_t))$$
を勾配降下法で最大化します。
online化?
さて、論文にはここまでしか記述がありませんが、上記のEMアルゴリズムをonlineで実行することはできるでしょうか?
M-stepの内のNeural Netに関する部分はミニバッチごとにパラメータを更新してもよさそうです。
しかし、ミニバッチサイズが小さい場合はミニバッチ内のデータのみを使用して$\pi$の更新を行うのはまずそうです。(例えばミニバッチ内に特定のラベルが含まれない場合は、すべてのリーフに付随する$\pi$のそのラベルに対応する値が0になってしまいます。)
そこで、今回はE-stepにおける$\pi$の更新に関して次の2パターンを試してみました。
1: ミニバッチごとに解析解を利用した指数移動平均で値を更新する。
batch normalizationの実装と同じイメージです。 つまりミニバッチごとに
\begin{align}
n_{l,t,k}&=\sum_{n=1}^{N^{\prime}}\delta(y_n=k)h_{n,l} \\
d_{l,t}&=\sum_{n=1}^{N^{\prime}}h_{n,l} \\
\end{align}
を計算して
\begin{align}
N_{l,t,k}&=an_{l,t,k} + (1-a)N_{l,t-1,k} \\
D_{l,t}&=ad_{l,t} + (1-a)D_{l,t-1} \\
(\pi_{l,t})_{k}&=N_{l,t,k} / D_{l,t}
\end{align}
と$\pi$を更新します。
2: 解析解は使用せずミニバッチごとに
\sum_{n=1}^{N^{\prime}}\sum_{l=1}^{L}h_{n,l}log((\pi_{l,t})_{y_n})
を微分してNeural Netのパラメータと同様に勾配降下法で更新する。
この手法をとる場合、$\pi_l = softmax(w_l)$となる変数$w_l$を導入して$\pi_l$の代わりに$w_l$を最適化しました。
まとめると次のようなコードになります。
for batch_idx, (data, target) in enumerate(train_loader):
if self.cuda:
data, target = data.cuda(), target.cuda()
data, target = Variable(data), Variable(target)
# forward path
self.update_nodes(data)
# e step
exp_dict = self._e_step(target, softmax=(m_step=='sgd'))
# m step
if m_step == 'ma':
#指数移動平均によるpiの更新 + netral netのbackward path
loss = self._m_step_ma(target, exp_dict, optimizer = optimizer)
else:
#pi+neural netのbackward path
loss = self._m_step_sgd(target, exp_dict, optimizer = optimizer)
計算量に関してですが、1 iteration毎にミニバッチに対して各Neural Netのforward path とbackward pathをそれぞれ1度ずつ計算すればよいので、そこまで重くはありません。
わざわざEMアルゴリズムで最適化する必要があるのか?
上記のように潜在変数を導入しなくても
L(\theta, X, Y) = \sum_{n=1}^{N}log(p(y_n|x_n))=\sum_{n=1}^{N}log(\sum_{l=1}^{L}(\pi_l)_{y_n}\mu_l(x_n,\theta))
は微分可能なので直接SGDで最適化できます。1 iteration内の各Neural Networkのforward pathとbachward pathの回数は上記EMアルゴリズムと同じ1回です。logの中にsumがあり、目的関数内で$\pi$達と各Neural Networkの出力の掛け算を分離できませんが、計算量的にEMアルゴリズムに劣っているわけではありません。今回はこちらの学習方法も試してみました。
実験
mnistを利用して実験を行いました。
上で説明したように、実験した最適化手法は
- EMアルゴリズム:em moving average($\pi$の更新は指数移動平均を用いる)
- EMアルゴリズム:em sgd($\pi$の更新は勾配降下法を用いる)
- 全てSGD : all sgd
の3つです。
実装にはPyTorchを用いました。上記3つのアルゴリズムはすべて学習における計算グラフは固定なので、動的な計算グラフ構築をサポートするPyTorchの真価を発揮したわけではないですが、こういった込み入ったアルゴリズムを実装するのにデバッグのしやすいPyTorchはとても使いやすかったです。
設定
- 決定木の構造は深さ4のbalanced treeで固定。(リーフ数16個)
- 各ノードに付随するNeural Netの構造は次のとおり
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 3, kernel_size=5)
self.conv2 = nn.Conv2d(3, 6, kernel_size=5)
self.fc1 = nn.Linear(6*16, 100)
self.fc2 = nn.Linear(100, 1)
self.gamma = 1
def forward(self, x):
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2(x), 2))
x = x.view(-1, 6*16)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return F.sigmoid(self.gamma * x)
- Neural Netのパラメータの初期値はすべてのパターンで共通
- ミニバッチサイズは10
- 学習係数の初期値は1, 0.1, 0.01, 0.001から最適なものを選択
- 3エポックごとに学習係数を1/10に
結果
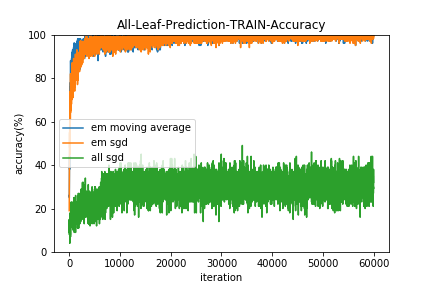
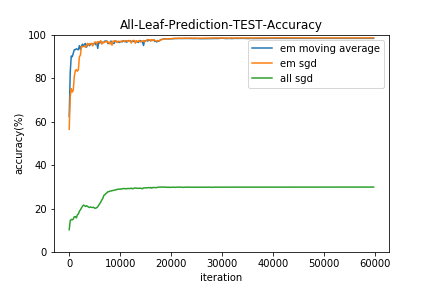
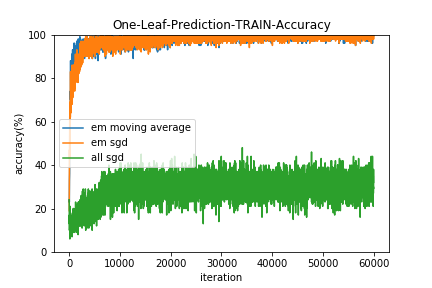
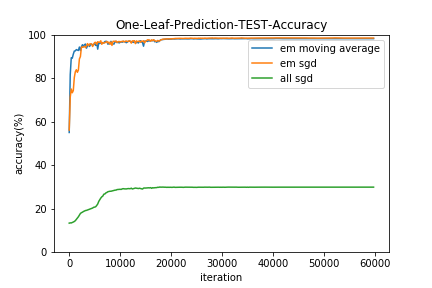
イテレーションごとに学習データとテストデータに対して、
- すべてのリーフを使用した予測の的中率(All-Leaf-Prediction)
- 1つのリーフのみ使用した予測の的中率(One-Leaf-Prediction)
すべてSGDで最適化する手法(all sgd)は、Neural Netの初期値を変えてみたり学習係数を広範囲探索してみたりバッチサイズを変えてみたり様々な勾配降下法の亜種をためしたりしたのですがうまくいきませんでした。。(コードは用検証ですが)
EMアルゴリズムは$\pi$の更新に移動平均を用いた方(em moving average)が若干収束は早いようです。
また、結果的にすべてのリーフを用いた予測(All-Leaf-Prediction)と1つのリーフのみ使用した予測(One-Leaf-Prediction)の的中率にほとんど差はみられませんでした。
結局「決定木の分かりやすさとNeural Networkの表現力」を兼ね備えたモデルが得られたのか?
通常の決定木が分かりやすいのは各ノードの分岐条件が分かりやすく記述できることが大きいです。しかし、今回紹介した手法では分岐関数にNeural Netを使用しているので、分岐条件を理解するにはもう1ステップNeural Netの予測理由を提示する手法等が必要になるのが欠点ですね。今回実験で使用したmnistは線形モデルでも90%以上の精度が出るうえ分岐関数に使用したCNNは予測理由の提示が一筋縄ではいかないので、本手法のありがたみは分りにくかったかもしれません。
文書分類問題などに応用し、分岐関数にAttentionつきRNNなどを用いた方が、面白いデモが作れそうです。
また、リーフにたどり着くまでにたどったパスは確認できるので、例えば「入力データが7か9であることまでは突き止めたが、7か9の分類でミスをした」など、どの段階で予測を間違えたか、などは分りやすいかと思います。
コード
https://github.com/nn116003/End-to-end-Learning-of-Deterministic-Decision-Trees
参考文献
[1]End-to-end Learning of Deterministic Decision Trees, arXiv preprint arXiv:1712.02743, 2017