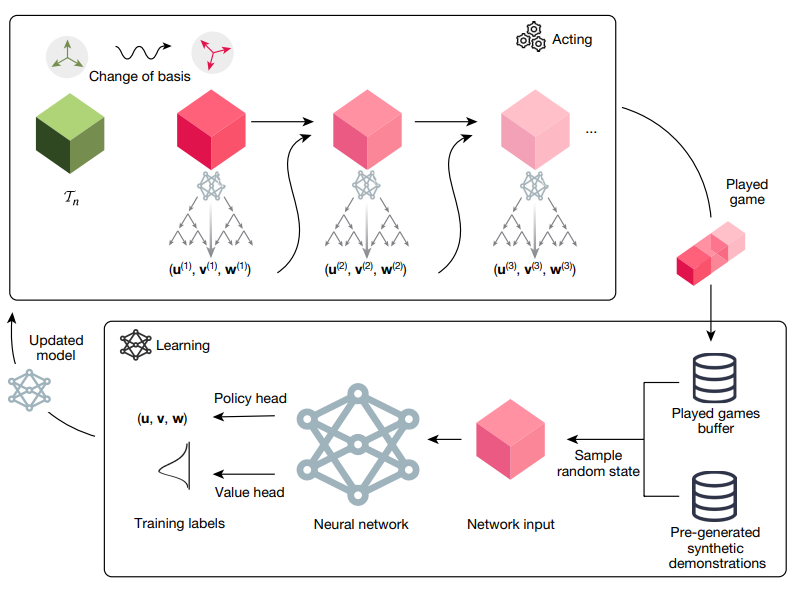
1. はじめに
本記事では、2022年10月にNatureに掲載されたAlphaTensor[1]および関連分野を紹介します。AlphaTensorは「AIが行列積演算の新しいアルゴリズムを発見した」といううたい文句のもとSNSを中心に大きな話題となりました。具体的には、[1]でAIが”発見”したアルゴリズムのひとつでは2進数上の4×4の行列の積を47回の掛け算で計算することができ、これは[1]以前の最速49回(Strassenのアルゴリズム)を上回ったことになります。なお、Strassenのアルゴリズムの49回はその発見から[1]まで約50年間破られていませんでした。
「AIが新しいアルゴリズムを発見した」という広告ですが、実際は 「あるテンソルのよい分解方法を強化学習を利用して探索した」 といった方が正しいです。この 「あるテンソル」はその分解方法と「行列積のアルゴリズム」が自然と対応付けられる ことが知られています。したがって「あるテンソルの”よい”分解方法」を探索することは「早い行列積のアルゴリズム」を探索することと等しくなります。ちなみに、この「あるテンソルのよい分解方法」を計算機を利用して探索することで、行列積の高速なアルゴリズムを見つけるという試みは、AlphaTensorが初ではなくこれまでさまざまな研究がなされています。
本記事の構成は以下のようになります。2章では[1]が利用している「特定の3次元テンソルの分解と行列積アルゴリズムの対応」を説明します。行列積演算アルゴリズムについての概観からはじめて、3次元テンソルの基本テンソルへの分解と行列積のアルゴリズムが対応することを説明します。またテンソルのランクと行列積アルゴリズムの計算量の関係を紹介します。3次元の「テンソル」が主役ですが、テンソル積などの線形代数の知識がなくても読めるように説明を試みました。2章の内容のより数学的に整理された記述は付録に回しました。3章では[1]において具体的にどのように新しいアルゴリズムを"発見"したか解説します。強化学習による探索の枠組みとAlphaTensorが利用したAlphaZeroという強化学習モデルおよび論文の実験結果を紹介します。4章ではAlphaTensorの結果とその周辺分野に対する自分の考えをまとめました。
2. テンソル分解と行列積のアルゴリズム
本章では、行列積のアルゴリズムとある3次元テンソルの分解との対応関係について説明します。簡易のため3次元テンソルを「3次元の行列=直方体状のグリッドに数字が入ったもの」として扱い、テンソル積などの線形代数の知識を必要としない説明を試みました。(本章の数学的に整理された内容は付録を参照のこと)
2.1. 行列積のアルゴリズム
本節では行列積の計算について、
- 一般によく使うアルゴリズム
- より高速なアルゴリズムの存在
- 計算回数の理論的な限界のみつもり
を簡単に解説します。
A=
\begin{pmatrix}
a_{1}^1 & a_{2}^1 \\
a_{1}^2 & a_{2}^2
\end{pmatrix},
B= \begin{pmatrix}
b_{1}^1 & b_{2}^1 \\
b_{1}^2 & b_{2}^2
\end{pmatrix},
C = \begin{pmatrix}
c_{1}^1 & c_{2}^1 \\
c_{1}^2 & c_{2}^2
\end{pmatrix}
\begin{pmatrix}
c_{1}^1 & c_{2}^1 \\
c_{1}^2 & c_{2}^2
\end{pmatrix} =
\begin{pmatrix}
a_{1}^1 & a_{2}^1 \\
a_{1}^2 & a_{2}^2
\end{pmatrix}
\begin{pmatrix}
b_{1}^1 & b_{2}^1 \\
b_{1}^2 & b_{2}^2
\end{pmatrix}
とします。
この時2×2の行列の掛け算$C=AB$は、通常以下のように行います。
c^1_1 = a^1_1 b^1_1 + a^1_2b^2_1 \\
c^1_2 = a^1_1 b^1_2 + a^1_2b^2_2 \\
c^2_1 = a^2_1 b^1_1 + a^2_2b^2_1 \\
c^2_2 = a^2_1 b^1_2 + a^2_2b^2_2 \\
この計算方法の場合、掛け算は8回行うことになります。同様にして、このような通常の行列積の計算では一般のサイズnの正方行列の積には$n^3$回の掛け算を実施することになります。
実は、この2×2の行列積の「8回」や一般の行列積における$n^3$回の掛け算は、減らすことができます!!
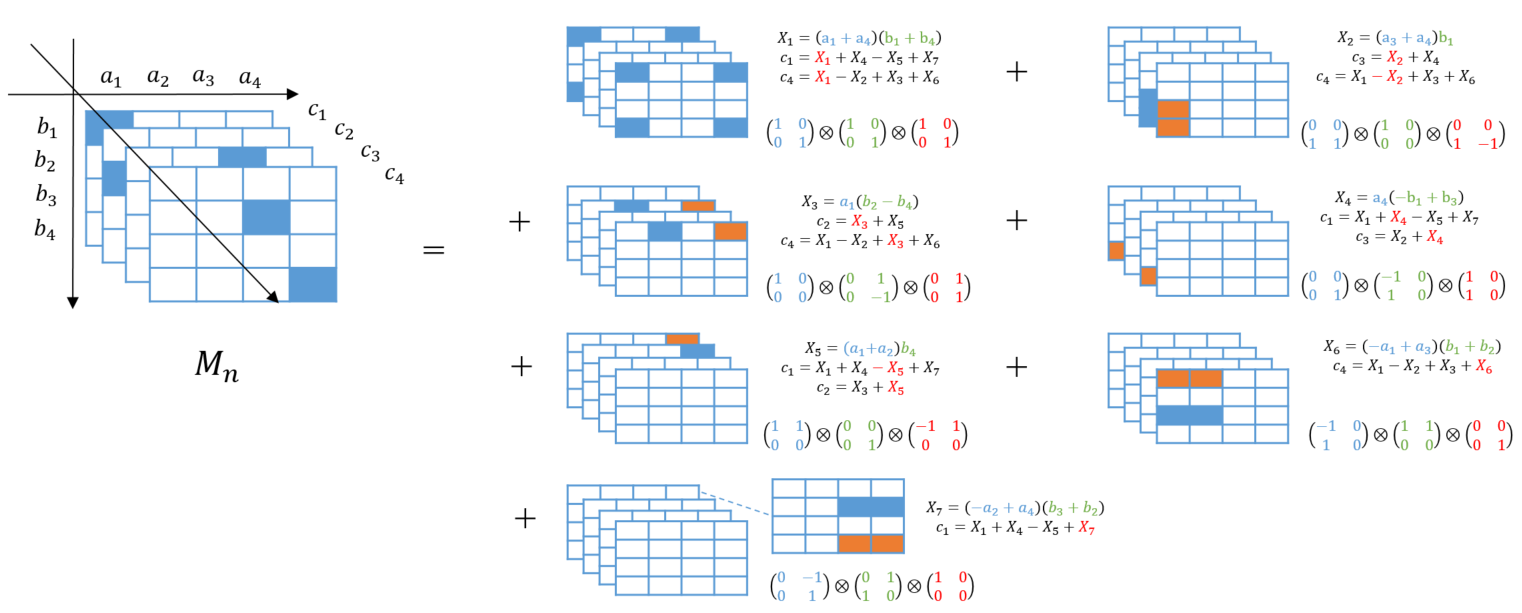
Strassenは[2]において、2×2の行列積を7回の積で計算する次のようなアルゴリズムを提案しました。($X_1,\dots,X_7$の計算でそれぞれ1回掛け算を行う。)
\begin{align*}
X_1 &=& (a^1_1+a^2_2)(b^1_1+b^2_2) \\
X_2 &=& (a^2_1+a^2_2)b^1_1 \\
X_3 &=& a^1_1(b^1_2-b^2_2) \\
X_4 &=& a^2_2(-b^1_1+b^2_1) \\
X_5 &=& (a^1_1+a^1_2)b^2_2 \\
X_6 &=& (-a^1_1+a^2_1)(b^1_1+b^1_2) \\
X_7 &=& (a^1_2-a^2_2)(b^2_1+b^2_2)
\end{align*}
\begin{align*}
c^1_1 &=& X_1 + X_4-X_5+X_7 \\
c^2_1 &=& X_2+X_4 \\
c^1_2 &=& X_3 + X_5 \\
c^2_2 &=& X_1 + X_3 -X_2+X_6
\end{align*}
行列を4分割することにより、Strassenのアルゴリズムを一般の行列の掛け算に再帰的に適用することができます。例えば4×4の行列の掛け算の際には、行列を2×2のブロック×4に分解し、そのそれぞれを行列の要素とみなしてStrassenのアルゴリズムを適用します。このとき$X_1,\dots,X_7$に対応する演算で2×2の行列の掛け算をそれぞれ1度実行するので、ふたたびStrassenのアルゴリズムを適用します。この場合$7^2=49$回の要素の掛け算で行列積が計算できます。同様にして、サイズ$2^k$の正方行列積は$7^k$回の掛け算で実行できます。したがって一般のサイズnの行列積は約$n^{\log_2(7)}\simeq n^{2.81}<n^3$回の掛け算で計算できることになります。(サイズが$2^k$でない場合は要素が0の行や列をたす)
さて、Strassenのアルゴリズムは2×2の行列積においては”最速”、つまり掛け算の回数を7回より減らすことができないことが証明されています[3]。いっぽう、それ以外のサイズの行列積に関しては最小掛け算数が分かっているものはないようです(2017年時点。2018以降の進展は調査しきれていません)[4]。ただ、一般のサイズnの行列に対して、その積の最小計算量$\omega$(exponent)を
\omega = inf\{h\in R | サイズnの行列積がO(n^h)で計算可能\}
とすると、2017年の段階で
2\leq\omega < 2.373
であることが証明されており[4][5]、再帰的なStrassenのアルゴリズムの適用より高性能なアルゴリズムの存在が示唆されています。($\omega$の上界を推定する論文では具体的なアルゴリズムは提案されないことが多い。)
コミュニティでは
\omega = 2
であること(つまり行列の足し算とほぼ同じオーダーで行列積が計算可能!!)が予想されており、そのアルゴリズムを求めてさまざまな試みがなされています[4]。
2.2. テンソル分解と行列積アルゴリズムの対応
この節では行列積のアルゴリズムを探索する際の一つの指針となる、テンソル分解との対応を説明します。結論としては 「あるテンソル」のR個の「ランク1テンソル」への分解が、行列積のアルゴリズムに相当し、その計算量はRが小さいほど少なくなります。 したがって、 できるだけ高速な行列積アルゴリズムの探索は、「あるテンソル」をできるだけ少ない「ランク1テンソル」の和に分解する方法の探索に等しい ということになります。
以下では簡易のためサイズnの正方行列の積について扱います。一般のサイズの行列積に関しても同様の議論が成り立ちます。。
2.2.1「あるテンソル $M_n$ 」
まず、
A=
\begin{pmatrix}
a_{1}^1 & a_{2}^1 \\
a_{1}^2 & a_{2}^2
\end{pmatrix},
B= \begin{pmatrix}
b_{1}^1 & b_{2}^1 \\
b_{1}^2 & b_{2}^2
\end{pmatrix},
C = \begin{pmatrix}
c_{1}^1 & c_{2}^1 \\
c_{1}^2 & c_{2}^2
\end{pmatrix}
とします。$a^i_j, b^i_j, c^i_j$に連番の添え字をふって改めて$a=(a_1,a_2,\dots), b=(b_1,b_2,\dots),a=(c_1,c_2,\dots)$とします。$C=AB$のとき、
c_k = \sum_{i,j}t^{i,j}_ka_ib_j
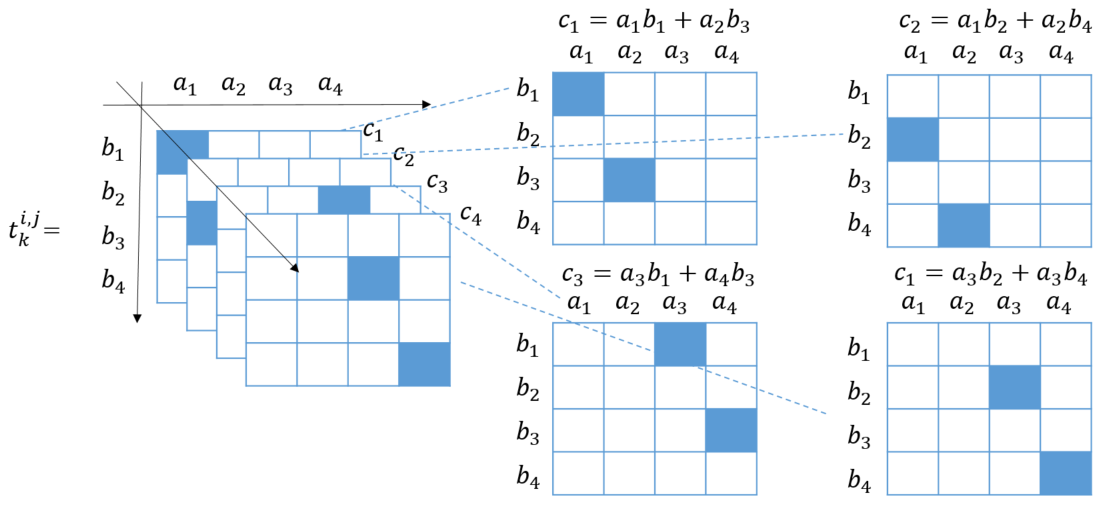
と書けるはずです。この$t^{i,j}_k$を、i成分が「ヨコ」j成分が「タテ」k成分が「奥ゆき」であるような3次元テンソルで表します。例えば行列のサイズが2×2の時、次のようになります。(色がついているセルが1それ以外は0)
\begin{pmatrix}
c_{1} & c_{2} \\
c_3 & c_4
\end{pmatrix} =
\begin{pmatrix}
a_{1} & a_{2} \\
a_3 & a_4
\end{pmatrix}
\begin{pmatrix}
b_{1} & b_{2} \\
b_3 & b_4
\end{pmatrix}
以降、 サイズnの行列に対してこのように $t^{i,j}_{k}$ たちを並べたテンソルを $M_{n}$ と書くこととします。
2.2.2. $M_n$の分解
一方、通常の行列積の計算方法およびStrassenのアルゴリズムを観察すると、$C=AB$の計算は
c_i = \sum_{r=1}^R w^r_i (\sum_ku^r_ka_k)(\sum_lv^r_lb_l) \tag{*}
の形をしていることが分かります。和の順番を変更すると、
c_i = \sum_{k,l} (\sum_{r=1}^R w^r_i u^r_kv^r_l)a_kb_l
となるので、$t^{i,j}_k(M_n)$の定義と見比べると、
t^{i,j}_k=(\sum_{r=1}^R w^r_k u^r_iv^r_j)
となります。
ここで、$w^r=(w^r_1,w^r_2,\dots),u^r=(u^r_1,u^r_2,\dots),v^r=(v^r_1,v^r_2,\dots)$とおき、
$w^r_k u^r_iv^r_j$を、i成分が「ヨコ」j成分が「タテ」k成分が「奥ゆき」であるような3次元テンソル状にならべたものを便宜的に
u^r\otimes v^r\otimes w^r
と書きます。これを ランク 1のテンソル とよびます。 $t^{i,j}_{k}$ を3次元テンソル状にならべたものを$M_{n} $と定義していましたが、$t^{i,j}_{k}=\sum_{r=1}^{R} w^{r}_{k} u^{r}_{i} v^{r}_{j}$ より $M_{n}$はランク 1のテンソルを使って
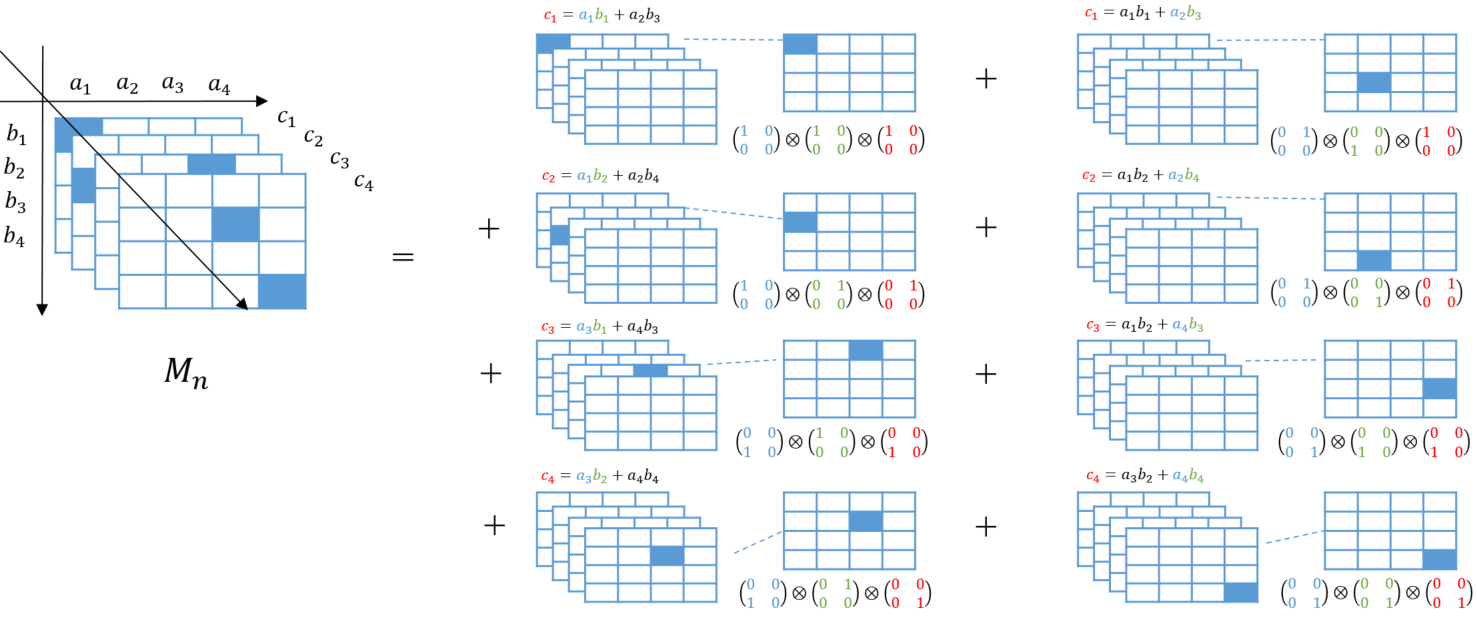
M_n=\sum_{r=1}^R u^r\otimes v^r\otimes w^r
と分解できることになります(下記の例参照)。よって (*)の形の行列積計算のアルゴリズムを与えることは、$M_n$をrank 1のテンソルの和に分解することに等しい ことになります。
例1:サイズ2の行列に対する通常の行列演算アルゴリズム
例2:サイズ2の行列に対するStrassenのアルゴリズム
青色=1、オレンジ=-1に対応
2.2.3. $M_n$の分解と行列積のアルゴリズムとテンソルのランク
これまでの議論をまとめると、$M_n$のランク 1テンソルへの分解$M_n=\sum_{r=1}^R u^r\otimes v^r\otimes w^r$が与えられれば、次のような行列積の計算アルゴリズムが定まることになります。
行列積計算アルゴリズム
\begin{align*}
& parameter: \quad
\{u^r,v^r,w^r\} \quad s.t. \quad M_n=\sum_{r=1}^R u^r\otimes v^r\otimes w^r \\
& input : \quad A,B \quad サイズnの行列 ({a_i},{b_j}:A,Bの要素)\\
& output : \quad C=AB \\
& (1) for ~ r ~ in ~ \{1\dots R\}: \\
& (2) \quad X_r = (\sum_k^{n^2}u^r_ka_k)(\sum^{n^2}_lv^r_lb_l) \\
& (3) for~i~in~\{1\dots n^2\}: \\
& (4) \quad c_i = \sum_r^R w^r_i X_r \\
& return ~C
\end{align*}
$u_k^r$と$a_k$の掛け算($v^r_l$と$b_l$の掛け算)は行列を定義する時点であらかじめ実行することができ、(2)では 実質R回 の掛け算が実行されます。(4)では$Rn^2$回の掛け算が発生し得ますが、通常の行列計算のアルゴリズムやStrassenのアルゴリズムのように$w^r_i\in\{-1,1\}$であれば(4)でも掛け算は発生しません。 できるだけRが小さい$M_n$の分解を見つけることができれば、より高速な行列積計算アルゴリズムを得ることになります。
前節の例でわかるように、サイズ2の行列積に対して、通常の行列積計算のアルゴリズムは$M_2$を8個のランク 1テンソルへ分解する方法に対応し、Strassenのアルゴリズムは$M_2$を7個のランク 1のテンソルへ分解する方法に対応します。このように、一般のテンソル$T$もランク 1のテンソルの和に分解することが可能ですが、その分解の仕方は一意ではありません。このような分解のうち、もっともランク 1のテンソルの数が少なくなる分解をした場合の、ランク1のテンソルの数をもとの テンソルのランク とよび $R(T)$ と書くことにします。$R(T)$は基底の変換に関して不変であり、行列のランクの自然な拡張になっています。
Def.
R(T) = inf\{R|T=\sum_{r=1}^R u^r\otimes v^r\otimes w^r\}
つまり、 サイズnの行列積の計算量の理論限界を求めることおよび、それを達成するアルゴリズムを見つけることは、$R(M_n)$を計算すること、$M_n$を$R(M_n)$個のランク1のテンソルへ分解する方法を見つけることとほぼ等しい ということになります。 実際、次が成り立ちます[2]。
Th.
inf\{\tau\in R|R(M_n)=O(n^\tau)\} = inf\{h\in R | サイズnの行列積がO(n^h)で計算可能\}
よく知られているように行列のランクはそれを計算するアルゴリズムが存在しますが、一般のテンソルの$R(T)$個のランク1のテンソルへの分解を求めることはNP hardであることが知られています。また$R(M_2)$=7(Strassenのアルゴリズム)は知られていますが、その他のサイズに関しては$R(M_3)$すら知られていないようです(2017時点の記述[4]。2018以降の進展は調べ切れていません)。
3. 強化学習による行列積アルゴリズムの探索
2章で行列積の高速なアルゴリズムを探索することは$M_n$をできるだけ少ないランク1のテンソルの和へと分解する方法を探索するに等しいということを説明しました。AlphaTensorはこの事実を用いて、強化学習で$M_n$の分解を探索しています。本章では具体的にどのようにこの分解を探索しアルゴリズムを「発見」したのか説明すします。※計算機を利用して$M_n$の分解を探索する試みはAlphaTensorが初ではないが既存研究はある程度のサイズについて有用な分解を見いだせていませんでした。[1]
3.1. 強化学習による探索
まず、強化学習モデルのアーキテクチャはブラックボックスとして、強化学習による$M_n$の分解方法の探索の大枠を説明します。
AlphaTensorでは$M_n$の分解をTensor Gameとよぶゲームに見立て、強化学習エージェントにTensor Gameを何度もプレイさせることによりその勝利方法=$M_n$の分解 を学習させることを試みています。
Tensor Game
\begin{align*}
& input:M_n \quad 分解したいテンソル \\
& agent:ゲームのプレイヤー。環境S_rを入力としてランク1のテンソルを返す\\
& reword:報酬\\
& (1) init ~ S_0=M_n, \quad reword_0=0\\
& (2) for~r~in~\{1\dots R_{max}\}: \\
& (3) \quad u^r \otimes v^r \otimes w^r = agent(S_{r-1}) \\
& (4) \quad S_r = S_{r-1}-u^r \otimes v^r \otimes w^r \\
& (5) \quad reword_r = reword_{r-1}-1 \\
& (6) \quad if~M_n=S_r: \\
& (7) \quad \quad break \\
& (8)if~r=R_{max}: \\
& (9) \quad reword_r = reword_r - \gamma(S_{R_{max}}) \\
& (10)return~ \{S_r\}, \{reword_r\}, \{u^r \otimes v^r \otimes w^r\}
\end{align*}
Tensor Gameではプレイヤーは、対象テンソルの分解の要素候補を提案していきます(4)。できるだけ少ない数での分解が目標なので、1提案するごとに-1のペナルティを受けます(5)。目標のテンソルと完全に一致する分解にたどり着くか、最大提案数に達すればゲームを終えます。最大提案数に達することでゲームを終えた場合は、提案の総和と対象テンソルの残差テンソル$S_{R_{max}}$に応じてさらにペナルティ$\gamma(S_{R_{max}})$を受けます(9)。$\gamma (S)$はテンソル$S$のランクの上界であり、$S$を”スライス”した各行列のランクの総和によって与えられます。なお、厳密な分解を求めることが目的であるため、$u,v,r$の要素は離散値$\{-2,-1,0,1,2\}$に限定しています。
このTensor Gameを強化学習エージェントが何度もプレイするなかで、(6)の条件によりゲームを終えた場合の出力を調べることで、$M_n$の少ない数のランク1テンソルでの分解(=高速な行列積アルゴリズム)が得られることが期待されます。
3.2. AlphaTensorのアーキテクチャ
本節ではAlphaTensorの強化学習モデルとしてのアーキテクチャを簡単に紹介します。
AlphaTensorはサンプルベースのAlphaZero[6]をTensor Gameに適用しています。
AlphaZeroに関しては下記のブログ記事の解説が分かりやすいです。
スッキリわかるAlphaZero | どこから見てもメンダコ
https://horomary.hatenablog.com/entry/2021/06/21/000500
ここではAlphaZeroについては簡単に概略のみ説明します。
AlphaZeroは基本的にMCTS(モンテカルロ木探索)を行いつつ、探索時の状態価値関数(将来の報酬の期待値)とpolicy(取るべき行動の分布)を学習する手法です。
MCTSとはゲームの状態がどれほどよいか、ある行動を起こすとどれほど状態がよくなるか、ある行動はどれほど試す価値があるのか、等を見積もりながらいわゆる先読みをする方法です。この際ノードでゲームの状態を、ノードから伸びるエッジでその状態での行動を表した木構造でデータを保持します。
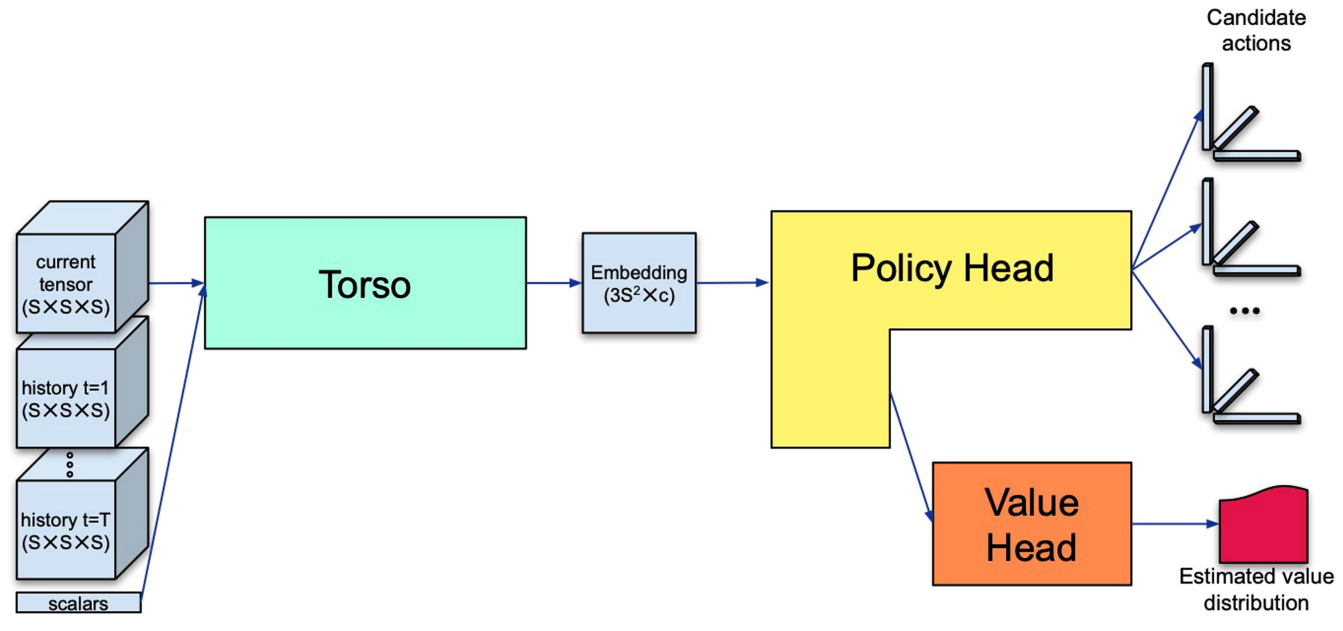
AlphaTensorのニューラルネットワーク(NN)はTensorGameにおける状態$\{S_1,\dots , S_{t}\}$とそれまでの行動$\{a_1=(u_1,v_1,w_1),\dots, a_t\}$を入力とし、状態価値関数の値の分布とpolicy$\pi (.|S)$を出力、それらをMCTSに利用します。
AlphaTensorで用いるNNの模式図:[1]より引用
MCTSの概略は以下の様になります。
- 探索木中のエッジ(状態$s$と行動$a$の組)に$N(s,a), Q(s,a), \hat \pi(s,a)$を保持しておく。ただし
$N(s,a)$:探索で訪れた回数
$Q(s,a)$:行動価値関数の値(NNにより計算)
$\hat\pi(s,a)$:NNによるpolicyの出力$\pi(.,s)$からK個actionをサンプリングし行動の経験分布(ヒストグラム)を作成したもの - 探索木中、ある状態$s$での行動$a$は次の値を最大化するように決定する。
argmax_a Q(s,a) + c\hat \pi(s,a)\frac {\sqrt{\sum_b N(s,b)}}{1+N(s,a)}
cは活用(第1項)と探索(第2項)のバランスを取るパラメータである。
MCTSによるTemsorGameのプレイ後、"なました"行動の経験分布$\pi(s,a)=N^{1/\tau(s)}(s,a)/\sum_b N^{1/\tau(s)}(s,b)$および実際の報酬の分布を直接教師値としてNNを更新します。
TensorGameにAlphaZeroを適用するイメージ:[1]より引用
その他細かい工夫
- 行動$a=(u,v,r)$の要素は離散値$\{-2,-1,0,1,2\}$に限定。
近似ではなく厳密なテンソルの分解を得ることが目的であるため。 - 学習時、Tensor Gameの入力に$M_n$だけではなく、一般の3次元テンソルも与える。
冗長に思えるが下の工夫との関連で性能の向上が見込める。 - 人工データでの教師あり学習とmix。
因数分解と同様に一般のテンソル$T$からその分解を得ることは困難だが、$\{u^r,v^r,w^r\}$から$T=\sum_{r=1}^R u^r\otimes v^r\otimes w^r$を計算するのは容易。そのため$\{u^r,v^r,w^r\},T$の組(必ずしもランクを与える分解ではないが)を大量に生成し、モデルを教師あり学習することが可能。 - 学習中対象テンソルの基底を取り替えることで”data argumentation”
- 学習中与えるテンソルのサイズはn×m×p。$n,m,p\leq 5$。n×mの行列とm×pの行列の掛け算に相当
- $n,m,p\leq 5$であるアルゴリズムの探索の後、それらを組み合わせてより大きな行列でのアルゴリズムの探索も行っている。
3.3. 既存研究との比較した際の利点
既存の$M_n$の分解を探索する試みは、連続値の最適化によって求めた分解を”丸める”ことで厳密な分解を得るものが多かったようです[1]。AlphaTensorは強化学習の枠組みを用いることで離散的な値のテンソルによる分解を効率よく探索することを達成しています(逆にAlphaZeroは連続値の行動空間の探索には向かない)。また、離散値の分解が探索できるので、実数環以外の環上での$M_n$の分解を探索できるという利点があります。実際AlphaTensorでは整数環$\mathbb{Z}$上での$M_n$の分解の他に2進数$\mathbb{Z}/2\mathbb{Z}$上での分解の探索も行っています。さらに、強化学習における「報酬」の設計の自由度を利用してさまざまな性質をもった分解を探索することが可能になりました。例えばアルゴリズムの「実際の実行時間」を報酬に加えることにより、特定のハードウェアで高速でアルゴリズムの探索も実行しています。
3.4. 結果 -実際に発見されたアルゴリズムのランクと速度-
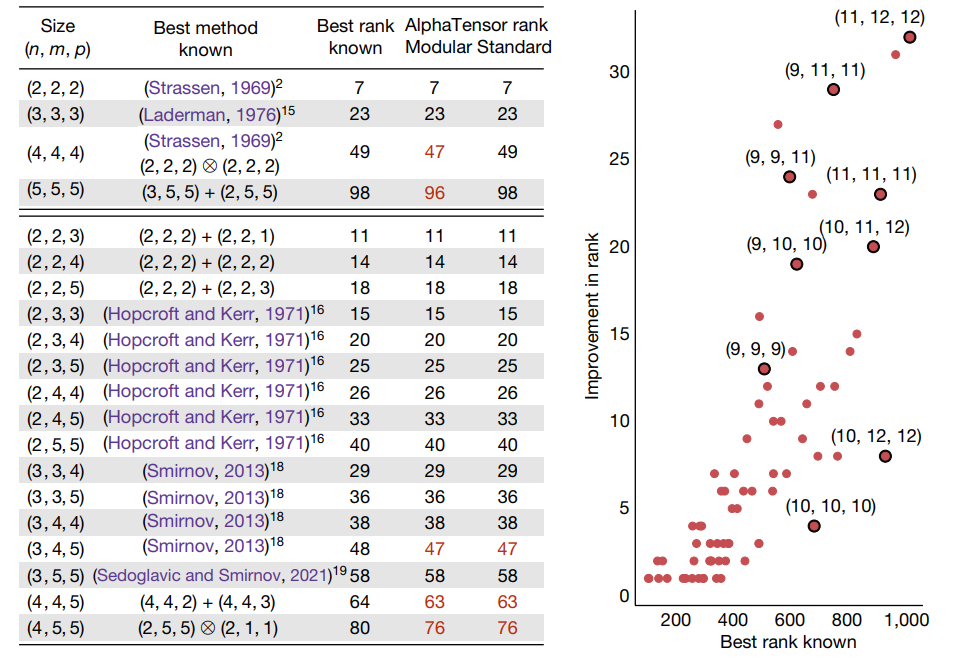
AlphaTensorによって発見された分解のランク
多くのサイズ$n,m,p\leq 5$で既存のbestランクと同等かそれ以上の結果が得れられています(左図:左図の"Modular"=2進数、"Standard"=整数)。それらを組み合わせることにより、より大きな行列積の計算において既存のアルゴリズムをより上回る結果となりました(右図)。
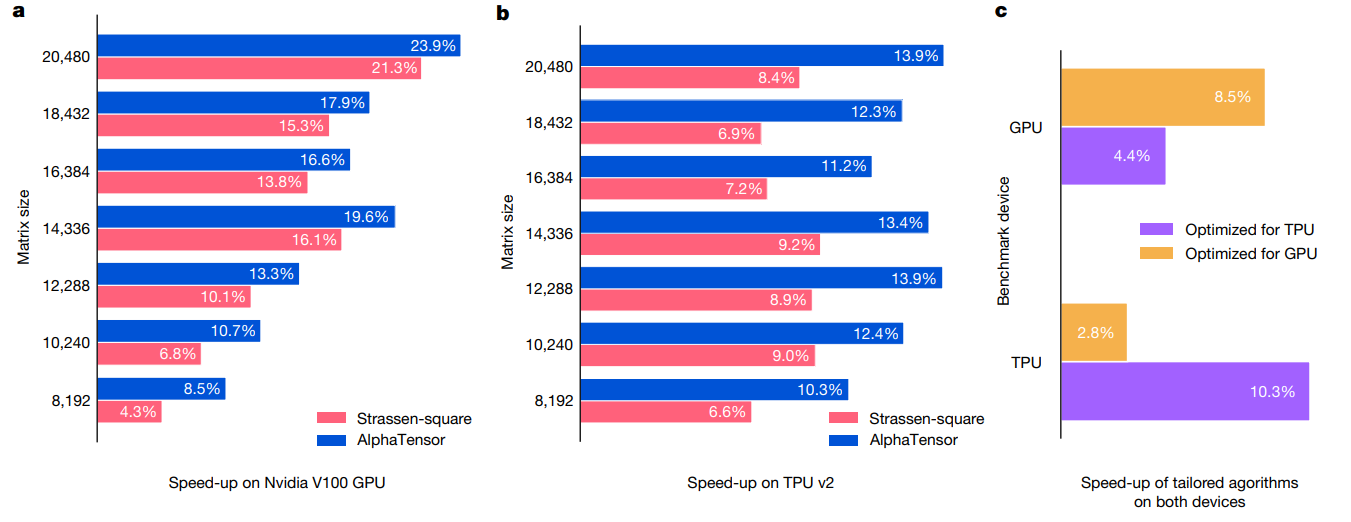
特定のハードウェア上の発見アルゴリズムの速度
AlphaTensor実行時、報酬に該当ハード上でのアルゴリズムの実行速度も追加して探索した結果。「実行速度」は微分不可能な指標ですが、強化学習の枠組みでは報酬として取り入れることが可能です。ハードウェアごとにチューニングされたアルゴリズムが得られました。
4. 考察
本論文について
「AIが人間が知らない新しいアルゴリズムを発見した」という宣伝文句ですが、実際実行しているのは以前から研究されている$M_n$の分解の探索です。ただ、既存研究では実用的な分解を探索できていなかった状況で実用的に高速なアルゴリズムを発見できたのは大きな進展といえます(既存の探索手法より真に優れているかどうかは、本論文の実験で利用しているTPUv3,v4×1週間という計算資源をそろえた比較が必要となります)。
また、行列分解のアルゴリズムの探索としては、
- 行動探索の範囲を$\{-2,-1,0,1,2\}$から広げた場合の検証
- 連続値での探索は本当にうまくいかないのか検証($M_n$の$\mathbb{Z}$上のランク=$M_n$の$\mathbb{R}$or$\mathbb{C}$上のランクなのか?)
といったことが気になりました。
一方、強化学習を利用した探索としては
- 数ある強化学習の手法の中でもAlphaZeroが本問題に対して真に効率的な探索手法なのか
といった疑問もあります。
強化学習による探索について
たびたび話題になるように、強化学習による「探索」が成功している分野は行列積アルゴリズムやゲームだけではないです。MolGAN[7]では特定の性質をもつ分子を生成するために、GANと強化学習を組み合わせています。[8]ではチップの設計に強化学習を用いていて実際にTPUの設計にも活用されたとのことです。
このように、なにか特別な性質をもったものを「探索」する工程でたびたび強化学習の成功例が報告されています。このような成功は、強化学習がベイズ最適化などの他の探索手法と比べて
- 探索の指標となる報酬を自由に設計できる
- 状態価値関数などの学習を通して探索空間の構造を理解することで、効率的な探索を行うことができる。(過去の施行で失敗した状況に似た状態は探索しない)
といった利点があるためであると考えています。
一方、ニューラルネットによる予測を含むため時間あたりの試行回数はランダムサーチとくらべて大きく劣るはずです。また探索の効率性は状態価値関数や報酬の的確さに左右されるため
- 状態の情報が不十分で状態価値関数の学習が難しい場合
- 殆どの行動で良い結果が得れれる場合
ような探索はランダムサーチなどの他の手法より劣ると予想されます。
いずれにせよ「$M_n$の分解」のような明示的な探索空間と適切な報酬が設定できれば、強化学習によって既存手法ではなし得なかった「発見」ができる可能性があることになります。日々の仕事や情報収集のなかで、このような条件を意識しておくことで、あらたな発見の芽をみつけることができるかもしれないですね。
5. 参考文献
[1] Fawzi, Alhussein, et al. "Discovering faster matrix multiplication algorithms with reinforcement learning." Nature 610.7930 (2022): 47-53.
[2] Volker Strassen, Gaussian elimination is not optimal, Numer. Math. 13 (1969), 354–356. MR 40 #2223
[3] S. Winograd, On multiplication of 2×2 matrices, Linear Algebra and Appl. 4 (1971), 381–388. MR 45 #6173
[4] Landsberg, J. M. Geometry and Complexity Theory 169 (Cambridge Univ. Press, 2017).
[5] Virginia Williams, Breaking the coppersimith-winograd barrier, preprint
[6] Silver, David, et al. "Mastering chess and shogi by self-play with a general reinforcement learning algorithm." arXiv preprint arXiv:1712.01815 (2017).
[7] De Cao, Nicola, and Thomas Kipf. "MolGAN: An implicit generative model for small molecular graphs." arXiv preprint arXiv:1805.11973 (2018).
[8] Mirhoseini, Azalia, et al. "A graph placement methodology for fast chip design." Nature 594.7862 (2021): 207-212.
付録: テンソルの分解と行列積アルゴリズム
2章では"テンソル"を単に多次元に数字が並んだもととして扱っていました。本付録ではもう少し数学的に整理して2章の内容をまとめ直します。
- テンソル積の定義
- $M_n$の定義
- $M_n$の分解と行列積アルゴリズムの対応
の順に整理し直します。以下線形空間はすべて$\mathbb{C}$上で有限次元のものを考えます。
テンソルというのは要は多重線形写像のことなのですが、正確にテンソル積を定義するために少し準備を行います。
Def. 双対空間
$V$を線形空間とする。このとき線形写像$f:V\rightarrow \mathbb{C}$全体のなす空間を$V$の双対空間とよび、$V^*$とかく。
また、$V$の基底を${e_i}$とした時、$e^i \in V^*$を$e^i(e_j)=\delta_{i,j}$として定義する。${e^i}$は$V^*$の基底となり、${e_i}$の双対基底とよぶ。
$\square$
特に$V^* \cong V$です。
Def. 多重線形写像
$A_1,\dots, A_n, B$を線形空間とする。このとき$f:A_1 \times \dots \times A_{n} \rightarrow B$が多重線形写像であるとは、任意の$a_i,a_i' \in A_i, x,y \in \mathbb{C}$に対して
f(a_1,\dots,xa_i+ya_i',\dots,a_n)=xf(a_1, \dots,a_i, \dots, a_n) + yf(a_1, \dots,a_i', \dots, a_n)
を満たすことをいう。$A_1 \times \dots \times A_{n} $から$B$への多重線形写像からなる集合を$L(A_1,\dots,A_n;B)$と書く。$\square$
$L(A_1,\dots,A_n;B)$は線形空間となります。特に$n=1$のときは単純な線形写像のなす空間です。また、${a_i^{s_i}|1 \leq s_i \leq dim(A_i)}$を$A_i$の基底、${b_i}$を$B$の基底とし、$E_{m_1,\dots,m_n;j} \in L(A_1,\dots,A_n;B)$を
E_{m_1,\dots,m_n;j}(a_1^{s_1},\dots,a_n^{s_n})=\prod_i\delta_{m_i,s_i}b_j
とすると${E_{m_1,\dots,m_n;j}}$はの$L(A_1,\dots,A_n;B)$基底になります。特に$dim(L(A_1,\dots,A_n;B))=dim(B)\prod dim(A_i)$です。
いよいよテンソル積の定義です。
Def. テンソル積
${A_i}$を線形空間とする。このとき
A_1 \otimes \dots \otimes A_n := L(A_1^*,\dots,A_n^*;\mathbb{C})
とし、$A_1 ,\dots, A_n$のテンソル積と呼ぶ。また、$a_i \in A_i$の時、$a_1 \otimes \dots \otimes a_n\in A_1 \otimes \dots \otimes A_n$を
a_1 \otimes \dots \otimes a_n(\alpha^1,\dots,\alpha^n):=\alpha^1(a_1)\dots\alpha^n(a_n)
で定める。$\square$
${a_i^{s_i}|1 \leq s_i \leq dim(A_i)}$を$A_i$の基底とすると$\{a_1^{s_1} \otimes \dots \otimes a_n^{s_n} |1\leq s_i \leq dim(A_i)\}$は$A_1 \otimes \dots \otimes A_n$の基底になります。特に$dim(A_1 \otimes \dots \otimes A_n)=\prod dim(A_i)$です。
また、$a_1^{s_1} \otimes \dots \otimes a_n^{s_n}\in A_1 \otimes \dots \otimes A_n$に
(a_1^{s_1} \otimes \dots \otimes a_n^{s_n})(\alpha^1,\dots,\alpha^{n-1}):=\alpha^1(a_1^{s_1})\dots\alpha^n(a_n^{s_{n-1}})a_n^{s_n}\in A_n
より定まる$L(A_1^*,\dots,A_{n-1}^*;A_n)$の元を対応させることで次がわかります。
Prop.
A_1 \otimes \dots \otimes A_n \cong L(A_1^*,\dots,A_{n-1}^*;A_n) \square
今後$A_1 \otimes \dots \otimes A_n$を$L(A_1^*,\dots,A_n^*;\mathbb{C})$や$L(A_1^*,\dots,A_{n-1}^*;A_n)$と同一視して
a_1 \otimes \dots \otimes a_n(\alpha^1,\dots,\alpha^n)=\dots \in \mathbb{C}
と書いたり
a_1 \otimes \dots \otimes a_n(\alpha^1,\dots,\alpha^{n-1})=\dots \in A_n
と書いたりします。
example.
$V$から$W$への線形写像の空間$L(V;W)$は$V^* \otimes W$と同一視できる。実際$v\otimes w\in V^* \otimes W$は上記の対応から線形写像$(v\otimes w )(x)=v(x)w$を定める。 $\square$
さて、$C^{nm}$をn行m列の行列全体のなす線形空間とします。このとき$C^{nm}$の元と$C^{ml}$の元の積をとるという操作は$C^{nm}\times C^{ml}$から$C^{nl}$への双線形写像とみなせます。このことから次のように行列積に対応するテンソルが定義できます。
Def. $M_n$
$M_{l,m,n}\in L(C^{nm}, C^{ml};C^{nl}) \cong C^{nm*}\otimes C^{ml*}\otimes C^{nl}$ を
M_{l,m,n}(A,B)=AB
として定義する。$M_{n,n,n}$を$M_n$と書く。$\square$
Remark. $M_n$と行列積のアルゴリズムの対応
$M_{l,m,n}=\sum_{r=1}^R u^r\otimes v^r\otimes w^r$なる$u^r\otimes v^r\otimes w^r\in C^{nm*}\otimes C^{ml*}\otimes C^{nl}$が与えられたとき、次のような行列演算のアルゴリズムが定まります。
\begin{align*}
& parameter: \quad
\{u^r,v^r,w^r\} \quad s.t. \quad M_{l,m,n}=\sum_{r=1}^R u^r\otimes v^r\otimes w^r \\
& input : \quad A,B \quad サイズnの行列 \\
& output : \quad C=AB \\
& (0) init \quad C=0 \\
& (1) for ~ r ~ in ~ \{1\dots R\}: \\
& (2) \quad X_r = u^r(A)v^r(B) \\
& (3) \quad C = C + X_r w^r \\
& return ~C
\end{align*}
Prop. 通常の行列積のアルゴリズム
$x_{i,j}\in C^{nm},y_{i,j}\in C^{ml},z_{i,j} \in C^{nl}$をそれぞれ$i,j$成分が1それ以外が0である行列とする。これらは$C^{nm}, C^{ml},C^{nl}$の基底となる。$x^{i,j},y^{i,j},z^{i,j}$をそれぞれの双対基底とする。
このとき
M_{l,m,n}=\sum_{i=1}^n \sum_{j=1}^m \sum_{k=1}^l x^{i,j}\otimes y^{j,k}\otimes z_{i,k}
$\square$
proof.
行列$A,B$の各成分を$a_{i,j},b_{i,j}$とする(つまり$a_{i,j}=x^{i,j}(A),b_{i,j}=y^{i,j}(B)$)。このとき
\begin{align*}
M_{l,m,n}(A,B) &= \sum_{i,k}(\sum_j a_{i,j}b_{j,k})z_{i,k} \\
&= \sum_{i,j,k} x^{i,j}(A)y^{j,k}(B)z_{i,k} \\
& = \sum_{i,j,k}x^{i,j}\otimes y^{j,k}\otimes z_{i,k} (A,B)
\end{align*}
$\square$
Prop. Strassenのアルゴリズム
$x_{i,j}$や$y_{i,j}$を$x^{i,j}$や$y^{i,j}$と同一視し、同じ行列の形で$C^{nm*}$の元を表しています。([4]の記述とは行列が転置関係になっていることに注意)
M_2 =
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \otimes
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \otimes
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
+
\begin{pmatrix}
0 & 0 \\
1 & 1
\end{pmatrix} \otimes
\begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \otimes
\begin{pmatrix}
0 & 0 \\
1 & -1
\end{pmatrix} \\
+
\begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \otimes
\begin{pmatrix}
0 & 1 \\
0 & -1
\end{pmatrix} \otimes
\begin{pmatrix}
-1 & 1 \\
0 & 0
\end{pmatrix}
+
\begin{pmatrix}
0 & 0 \\
0 & 1
\end{pmatrix} \otimes
\begin{pmatrix}
-1 & 0 \\
1 & 0
\end{pmatrix} \otimes
\begin{pmatrix}
1 & 0 \\
1 & 0
\end{pmatrix} \\
+
\begin{pmatrix}
1 & 1 \\
0 & 0
\end{pmatrix} \otimes
\begin{pmatrix}
0 & 0 \\
0 & 1
\end{pmatrix} \otimes
\begin{pmatrix}
-1 & 1 \\
0 & 0
\end{pmatrix}
+
\begin{pmatrix}
-1 & 0 \\
1 & 0
\end{pmatrix} \otimes
\begin{pmatrix}
1 & 1 \\
0 & 0
\end{pmatrix} \otimes
\begin{pmatrix}
0 & 0 \\
0 & 1
\end{pmatrix} \\
+
\begin{pmatrix}
0 & -1 \\
0 & 1
\end{pmatrix} \otimes
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix} \otimes
\begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix}
Def. テンソルのランク
テンソル$T$のランク$R(T)$を
R(T)=inf\{R|\exists a_i^j\in A_i \quad s.t. \quad T=\sum_{i=1}^Ra_1^i\otimes \dots \otimes a_n^i\}
とくに$T\in A_1\otimes \dots \otimes A_n$に対して$a_i\in A_i$が存在して、$T=a_1\otimes \dots \otimes a_n$と書けとき$R(T)=1$となる。$\square$
$M_{l,m,n}$の分解と対応する行列積のアルゴリズムの形から分かるように、$R(M_{l,m,n})$を与える分解に対応するアルゴリズムが最もfor文が短くなります。通常の行列積計算のアルゴリズムから$R(M_{l,m,n})\leq lmn$が分かります。またStrassenのアルゴリズムから$R(M_2)\leq 7$が分かりますが、[3]により$R(M_2)=7$が示されました。[4]によると$R(M_3)$については2017年の段階では分かっていないようです。(2018以降の進展に関しては調べ切れていません。)