自分が論文読んだ時のメモ書き的な物.
Qiitaに上げるようなものではないけど,はてブロだと数式が書きずらかったのでこっちで書いておく.
そもそも
- Recovering High Dynamic Range Radiance Maps from Photographs
- HDR画像:High Dynamic Range画像(輝度値が実世界の放射照度と比例している)
- この論文は,従来の機器で撮った写真HDR輝度マップを復元する手法について
HDR画像を生成する手順は,
- 露出を変えた複数の画像から画像を作る際の応答関数を予測
- それを使って複数の画像を、ピクセル値がそのシーンの真の輝度に比例する一つの画像に融合する
イントロ
- シーンの放射輝度が画像内のピクセル値になる方法を決める、非線形マッピングがある、わかんないけど
- 非線形マッピングを事前に知るのは難しい
- それは画像化の途中で複数の非線形マップが組み合わさっているから
アルゴリズム
まずフィルム写真の場合を考えていく.
露出の変化に対するフィルムの応答はcharacteristic curve(or Hurter-Driffield curve)に要約される.
characteristic curve: 処理後のフィルムの光学濃度$D$を、それが受けた露光$X$の対数に対してグラフにしたもの
$D$: optical density
$X$: exposure
$X$はフィルムでの放射照度$E$と露光時間の差$\Delta t$の積として定義され、その単位は$Jm^{-2}$.
ここで大事なのは,$E \Delta t$だけが重要であるという仮定であり,$E$を半分にして$\Delta t$を倍にしても、$X$が変わらないので光学密度$D$も変わらない点.
- $\Delta t$ が非常に大きい/小さいような極端な状況下では$\Delta t$と$E$の関係は崩れ,
reciprocity failure(相反則不軌)と呼ばれる - 相反則不軌が起こると具体的にこんな感じ(写真が載ってたサイト)になるらしい
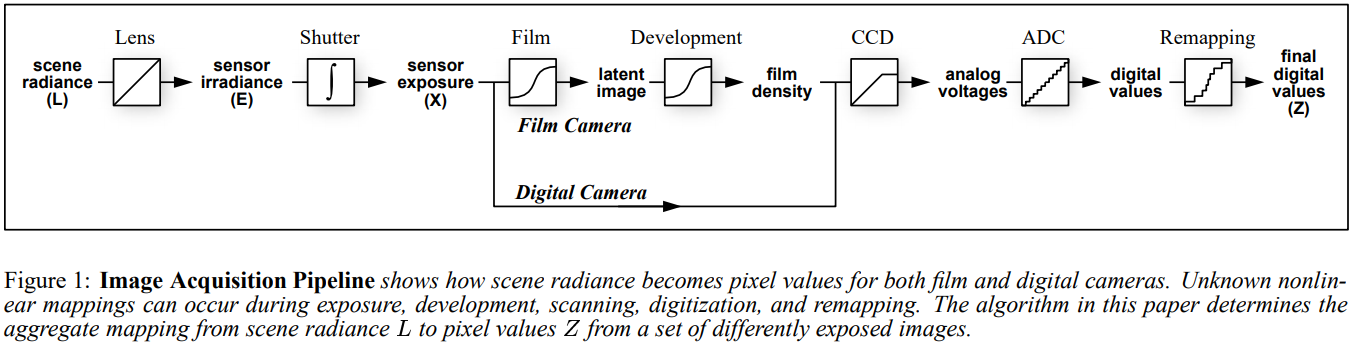
現像してデジタル化した後に,元の露出である$X$を非線形関数に通したと考えられる$Z$が得られ,その非線形関数を$f$と呼ぶ. この$f$を回復するのが一つ目のゴール! $f$は下図のような後処理の為の非線形な特性カーブの集まり.
論文 Figure 1より引用
$f$がわかればピクセル毎の露出を$X = f^{-1}(Z)$として計算でき,$f$は単調増加であることが考えられるので,$f^{-1}$は定義できると考えられる.
$f$を回復するために放射照度$E$を考えると,露出$X$と露出時間$\Delta t$がわかれば,放射照度$E = X/\Delta t$として回復できる.
また,$E$はシーンの輝度$L$に比例し,露出$X$は波長$X(\lambda)$の関数として,特性曲線の横軸は積分$\int X(\lambda)R(\lambda)d\lambda$で,$R(\lambda)$はピクセル位置におけるセンシング素子のスペクトル応答であると考えられる.
このアルゴリズムへの入力は,同じ場所から違う露出時間$\Delta t_j$(シャッタースピード)で撮られた複数のデジタル画像です.
また,撮られるシーンは静的であり,光の変化が安全に無視できるほど素早く一連の動作が完了することを仮定する.
その仮定により,フィルムの各画素$i$に対する放射強度値$E_i$は一定であると仮定できる.
ピクセル値を$Z_{ij}$と表示し,$i$はピクセル上の空間インデックス,$j$は露出時間$\Delta t_j$上のインデックスとすると,フィルムの相互関係は以下のように書ける.
$$ Z_{ij} = f(E_i\Delta t_j) \tag{1}$$
$f$が単調で,可逆と仮定すると,式(1)は下のように書き直せる.
$$ f^{-1}(Z_{ij}) = E_i\Delta t_j $$
両辺に自然対数をかけると
$$ \ln f^{-1}(Z_{ij}) = \ln E_i + \ln \Delta t_j $$
簡単化のために,$g = \ln f^{-1}$と定義すると,式(2)のようになる.
$$ g(Z_{ij}) = \ln E_i + \ln \Delta t_j \tag{2}$$
一連の式の中で$Z_{ij}$と$\Delta t_j$は既知です.
不明なのは,放射照度$E_i$と関数$g$であり,$g$は滑らかで単調であると仮定できる.
結局,関数$g$($f$の逆関数の対数をとったもの)と放射照度$E_i$を復元したい.
なので,最小二乗法で,式(2)から出来る方程式を最も満足するものを出す.
$g$の復元には,有限のピクセルの輝度値$Z$の定義域から$g(Z)$が取り得る有限の値を復元するだけで良いと考えられる.
$Z_{min}$と$Z_{max}$が許すのは整数の最小と最大のピクセル値であり,例えば8bit(256階調)の画像であれば(0, 255)と考えられる.
以下の二次目的を最小化する$g(Z)$の$(Z_{max} - Z_{min} + 1)$の範囲の値と,$\ln E_i$の$N$の値を見つけることを問題とする.
$N$はピクセルの位置の数で,$P$は写真の数.
C = \sum^N_{i=1}\sum^P_{j=1}[g(Z_{ij} - \ln E_i - \ln \Delta t_j]^2 + \lambda \sum^{Z_{max}-1}_{z=Z_{min}+1} g''(z)^2 \tag{3}
第1項は,解が最小二乗法で,式(2)より出る一組の方程式が満足することを保証する. 第2項は,関数$g$がなめらかであることを保証するための,$g$の二回微分の二乗の合計に関するなめらさの項. $g''(z) = g(z-1) - 2g(z) + g(z+1)$とする. この滑らかさの項は,最小化における,$g(z)$の間の結合を提供するという点で非常に重要.(らしい,ちょっと自分はよく理解できてない) スカラ$\lambda$はデータフィッティング項に関係する滑らかさの項に重み付けする.
$C$の最小化は簡単な線形最小二乗問題であり,線形方程式の優決定系はSVD法を使うことでロバストに解かれます. アルゴリズムに関する説明を完全にするために3点追加があり,一つ目は,$g(z)$と$E_i$の解は単一のスケールファクタ$\alpha$次第である事. もし,それぞれのlog放射照度$\ln E_i$が$\ln E_i + \alpha$に置きかわり,関数$g$が$g + \alpha$に置き換われば,連立方程式(2)と目的関数$C$にもまた変化はない. スケール要素を定義することにより,$g(Z_{min}) = 0 \hspace{1cm} ,where \hspace{5mm} Z_{min} = 0.5(Z_{min} + Z_{max})$という追加の制約を,これを線形系の方程式として追加するだけで導入することが出来る. この制約の意味は,$Z_{min}$と$Z_{max}$の中間の値を持つピクセルは単位露光を持つと仮定すること. 2つ目は,応答関数の基本的な解を予測することによって,解をよりよくfitさせることが出来ること. $g(z)$は,典型的に$Z_{min}$,$Z_{max}$周辺に,急こう配を持っているので,$g(z)$は滑らかさが少なくなり,これらの両極端近くではデータの近似性が悪くなる. そのため,なめらかさに重きを置き,曲線の中央に近くなるようにフィットするように,重み関数$\omega(z)$導入する. $\omega(z)$は,単純なhat関数.
\omega(z) = \left\{
\begin{array}{}
z - Z_{min} \hspace{1cm} for \hspace{5mm} z \leq \frac{1}{2}(Z_{min} + Z_{max}) \\
Z_{max} - z \hspace{1cm} for \hspace{5mm} z > \frac{1}{2}(Z_{min} + Z_{max})
\end{array} \tag{4}
\right.
これによって,現在の式3は
C = \sum^N_{i=1}\sum^P_{j=1}\{\omega(Z_{ij})[g(Z_{ij} - \ln E_i - \ln \Delta t_j)]\}^2 + \lambda \sum^{Z_{max}-1}_{z=Z_{min}+1} [\omega(z) g''(z)]^2
最後にこの解法ではすべての使用可能なピクセルを使用する必要はありません.
与えられた$P$写真数の$N$ピクセルの寸法を考えると,$\ln E_i$の$N$個の$g$の$(Z_{max} - Z_{min})$サンプルを解く必要があります.
十分にシステムを決定できる保険を掛けると,$N(P-1) > (Z_{max} - Z_{min})$位.
ピクセル値の範囲が255,$P=11$画像の場合,50ピクセル程度の$N$で十分.
しかし,ピクセル位置は,$Z_{min}$から$Z_{max}$まで合理的に均等に選ばれるべきであり,画像内に空間的に良く分布するべき.
そのうえ,放射輝度は画像の領域において一定であると仮定できるように,ピクセルは画素は輝度の分散が小さい画像の領域から良くサンプルされることが最良であり,イメージシステムのぼんやり見える影響が最小化されます.
こんな感じで応答曲線$g$を求めるらしい.
一応,論文の最後に著者が使った$g$を求めるためのMATLABコードが付録としてついていた.
結局,どうやってHDR画像作んねん!
上のアルゴリズムを使って応答曲線$g$が回復されたら,露出時間$\Delta t_j$が既知であると仮定した場合,関係する輝度値にピクセル値を素早く変換できる.
$g$は応答曲線を回復するために使った画像だけでなく,$g$を求めるために使った機器で撮った他の画像にも使える.($g$は機器固有のものだから)
HDR画像の各ピクセルの値になる$E_i$は,式2から
\ln E_i = g(Z_{ij}) - \ln \Delta t_j \tag{5}
のように求められる.
しかし,ロバスト性のため,HDR輝度値を回復するために,個々の画素の輝度値を計算するために全ての利用可能な露出を使うべき!
なので,画素値が応答関数の中央に近い露光に高い重みを与えるために,式4の重み関数を再利用して以下のように$E_i$を求める.
\ln E_i = \frac{\sum^{P}_{j=1}\omega(Z_{ij})(g(Z_{ij})-\ln \Delta t_j)}{\sum^{P}_{j=1}\omega(Z_{ij})} \tag{6}
終わり
論文には,他にも「$g$の推定には何枚の画像が必要なんだろう?」とか「絶対輝度を得るには」とか「カラー画像の場合の処理の仕方」とか書いてあったけど,読めてない.
あと,正直最小二乗法で求めるところらへんを理解しきれていないので,違っていたら教えてください.
違ってなくてもなんかあったらドシドシ言ってください.