IC555
参考
CR直列回路の過渡現象

-
初期条件
- t = 0 のとき、Vc = 0 => q = 0
-
計算
-
$ E = V_R(t) + V_C(t) \hspace{50pt} \cdots (キルヒホッフの第2法則) $
-
$ i(t) = \frac{dq(t)}{dt} \hspace{80pt} \cdots (電流は電荷の時間変化) $
-
$ V_R(t) = R \cdot i(t) = R \cdot \frac{dq(t)}{dt}$
-
$ V_C(t) = \frac{1}{C}\int i(t)dt = \frac{1}{C}\int (\frac{dq(t)}{dt}) dt = \frac{1}{C} q(t)$
上記から
$ E = R \cdot \frac{dq(t)}{dt} + \frac{q(t)}{C} \hspace{40pt} \cdots(微分方程式の変数分離型) $$ \frac{dq(t)}{dt} = \frac{CE - q(t)}{CR}$
$ \frac{1}{CE - q(t)} dq(t) = \frac{1}{CR} dt \hspace{33pt} \cdots 左にqを、右にtをもってくる$
$ \int \frac{1}{CE - q(t)} dq(t) = \int \frac{1}{CR} dt \hspace{20pt} \cdots 両辺積分する $
左辺
$ k = CE-q(t) $とすると、両辺微分して、 $ dk = -dq(t) => dq(t) = - dk$ となる$ \int \frac{1}{CE - q(t)} dq(t) = \int \frac{1}{k} (-dk) = -\int \frac{1}{k} dk = -\ln{k} = -\ln \bigl( CE-q(t) \bigr) + A'$
右辺
$ \int \frac{1}{CR} dt = \frac{t}{CR} + A''$
よって
$ \ln \bigl( CE-q(t) \bigr) = -\frac{t}{CR} + A \hspace{20pt} \cdots(Aは積分定数) $
$ CE - q(t) = e^{-\frac{t}{CR} + A} = e^{-\frac{t}{CR}} \cdot e^A = B \cdot e^{-\frac{t}{CR}} \hspace{20pt} \cdots(Bは積分定数を書き換え B = e^A)$
$ q(t) = CE - B \cdot e^{-\frac{t}{CR}} $
初期条件より t=0 のとき q=0
$ 0 = CE - B \cdot e^{-\frac{0}{CR}} = CE - B \hspace{20pt} \therefore B = CE $
$ q(t) = CE(1 - e^{-\frac{1}{CR}t}) $
$ i(t) = \frac{dq(t)}{dt} = \frac{d}{dt} \lbrace CE(1 - e^{-\frac{1}{CR}t}) \rbrace = \frac{d}{dt} \lbrace - CE \cdot e^{-\frac{1}{CR}t}) \rbrace = \frac{CE}{CR} \cdot e^{-\frac{1}{CR}t} = \frac{E}{R} \cdot e^{-\frac{1}{CR}t} $
$ V_R(t) = R \cdot i(t) = R \cdot \frac{E}{R} \cdot e^{-\frac{1}{CR}t} = E \cdot e^{-\frac{1}{CR}t} $
$ V_C(t) = \frac{1}{C}q(t) = \frac{1}{C} \cdot CE(1 - e^{-\frac{1}{CR}t}) = E \cdot (1 - e^{-\frac{1}{CR}t}) $
-
-
結果
- $V_C(t) = E(1 - e^{-\frac{1}{CR}t})$
- $V_R(t) = E \cdot e^{-\frac{1}{CR}t}$
- $i(t) = \frac{E}{R} \cdot e^{-\frac{1}{CR}t}$
- $q(t) = CE(1 - e^{-\frac{1}{CR}t})$
ピン配列
| pin | 名称 | 用途 |
|---|---|---|
| 1 | G | グランド |
| 2 | $\overline{TRIG}$ | タイマーの場合はスタート |
| 3 | OUT | 出力 |
| 4 | $\overline{RESET}$ | リセット |
| 5 | CONT | 内部電圧調整用 |
| 6 | THRES | 閾値(電源電圧の2/3) |
| 7 | DISCH | 電流調整用(コンデンサに電荷を貯める用) |
| 8 | Vcc | 電源5V程度 |
モード
- 単安定(モノステーブル)モード:タイマー
- 無安定(アステーブル)モード:発振器
- 双安定(バイステーブル)モード:ドライバなど
タイマー
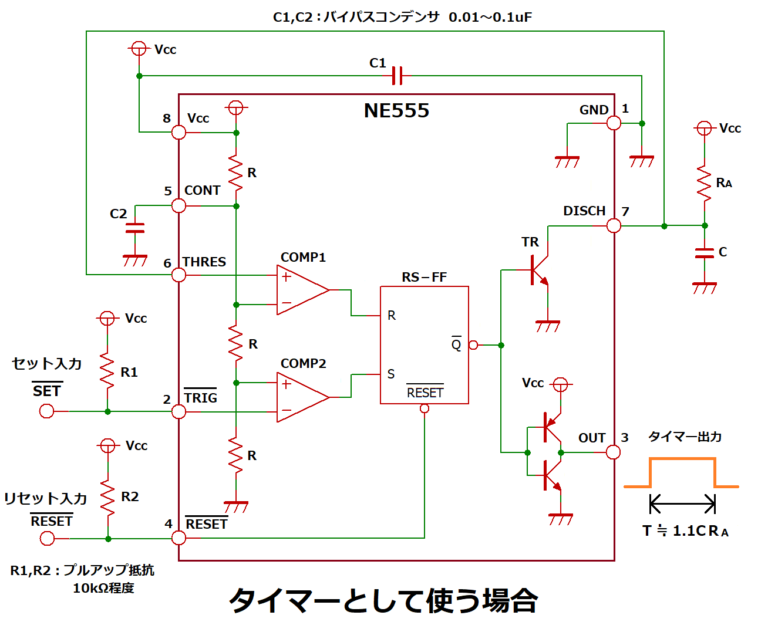
- RESET: プルアップ(10kΩ)。Lowでリセット
- TRIG: プルアップ(10kΩ)。Lowでタイマースタート
- CONT: 使用しないので、安定化のためにパイパスコンデンサ(0.1μF)を繋ぐ。
- THRES: DISCH と接続する
- DISCH: 抵抗Ra と コンデンサ C で分圧したところにつなぐ
- Vcc - Ra + C - GND
タイマーの時間は、C の電圧をTHRESに接続しているので、電源の2/3 になるところとなる。
すなわち C と Ra の直列回路の充電が電源の2/3になる時間。
$Vcc(1-e^{\frac{-t}{CRa}}) = \frac{2}{3}Vcc$
$1-e^{\frac{-t}{CRa}} = \frac{2}{3}$
$e^{\frac{-t}{CRa}} = \frac{1}{3}$
$t = -CRa \cdot ln\frac{1}{3} = CRa \cdot ln3 \fallingdotseq 1.1 \cdot CRa $
Ra: 1kΩ ~ 10MΩ程度
C : 0.001μF ~ 100μF程度
t : 10μS ~ 10s 程度
1秒の場合:
10kΩ + 0.01μF
100kΩ + 0.1μF
発振器

Highの時間は、C の電圧が電源の1/3 から 2/3 まで充電される時間となる。
Lowの時間は、C の電圧が電源の2/3 から 1/3 まで放電される時間となる。
- Highの時間
$ \frac{2}{3} \cdot Vcc(1-e^{\frac{-t}{C(Ra + Rb)}}) + \frac{1}{3}Vcc = \frac{2}{3}Vcc $
$ 1-e^{\frac{-t}{C(Ra + Rb)}} = \frac{1}{2} $
$ e^{\frac{-t}{C(Ra + Rb)}} = \frac{1}{2} $
$ t = -C(Ra + Rb) \cdot ln \frac{1}{2} = C(Ra + Rb) \cdot ln2 \fallingdotseq 0.69 \cdot (Ra + Rb)C $
- Lowの時間
$ \frac{2}{3} \cdot Vcc \cdot e^{\frac{-t}{C Rb}} = \frac{1}{3}Vcc $
$ e^{\frac{-t}{C Rb}} = \frac{1}{2} $
$ t = -CRb \cdot ln \frac{1}{2} $
$ t = CRb \cdot ln 2 \fallingdotseq 0.69 \cdot Rb C$
- トータル時間
$ t = 0.69 \cdot (Ra + Rb)C + 0.69 \cdot Rb C = 0.69 \cdot (Ra + 2Rb)C $
- 周波数
$ f = \frac{1}{ 0.69 \cdot (Ra + 2Rb)C } = 1.44 / (Ra + 2Rb)C $
- デューティ比
$ duty = \frac{0.69 \cdot (Ra + Rb)C}{0.69 \cdot (Ra + 2Rb)C} = \frac{Ra + Rb}{Ra + 2Rb} $
ポイント
-
デューティ比を50%に近づけるには
Ra を Rb より十分に小さくする($ Ra \ll Rb $)
ただし、Ra はあまり小さくしすぎない。
※Rb を Ra の10倍以上にすると50%に近くなる -
電源 5V の場合、1kΩ程度が目安。
Ra には最大で電源電圧がかかり、Pin7に大きな電流が流れるのでそれを考慮した大きさにする。 -
ex) $ Ra: 1kΩ, Rb: 10kΩ, C: 100μF の場合$
$ f = 1.44 / (1 * 10^3 + 2 * 10 * 10^3) 100*10^{-6} = 1.44 / 21 * 10^{-1} = 14.4 /21 = 0.68 Hz $
$ t = 1 / f = 1 / 0.68 = 1.47 sec $