フリップフロップ

データの記憶の機能を実現するもの

• $R$ : リセット
• $S$ : セット
• $Q$ : 出力
• $\overline{Q}$ : 反転出力

参考

• 【早わかり電子回路】順序回路とは？フリップフロップの種類と同期の方法を学ぶ

用語

• 順序回路 :現在の入力に加えて、過去の入力により出力を決定する論理回路
• 組み合わせ回路:

種類

• RSフリップフロップ
• JKフリップフロップ
• Dフリップフロップ
• Tフリップフロップ

RSフリップフロップ

• S=1, R=0 => S=0, R=0 で1がセットされる
• S=0, R=1 => S=0, R=0 で0がセットされる
• S=1, R=1 は使用禁止

S	R	Q前	Q#前	Q後	Q#後	動作
0	0	0	x	0	1	保持
0	0	1	x	1	0	保持
1	0	0	x	1	0	1
1	0	1	x	1	0	1
0	1	0	x	0	1	0
0	1	1	x	0	1	0
1	1	0	x	0	0	使用禁止
1	1	1	x	0	0	使用禁止

JKフリップフロップ

• JKフリップフロップの真理値表や回路図を簡単に解説！

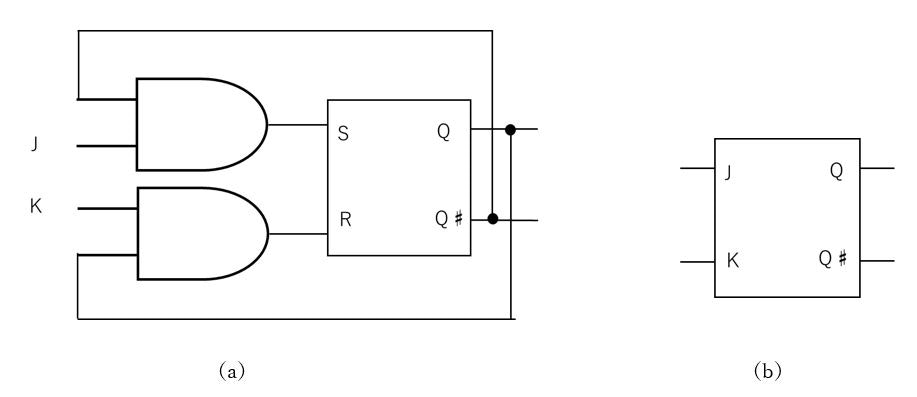
RSフリップフロップでは、S=1,R=1 が禁止動作だったが、これを"反転動作"する機能に変更したもの。

• J=0, K=0 のとき

  • Q=0 => S=0, R=0 => Q=0
  • Q=1 => S=0, R=0 => Q=1

• J=1, K=0 のとき

  • Q=0 => S=1, R=0 => Q=1
  • Q=1 => S=0, R=0 => Q=1

• J=0, K=1 のとき

  • Q=0 => S=0, R=0 => Q=0
  • Q=1 => S=0, R=1 => Q=0

• J=1, K=1 のとき

  • Q=0 => S=1, R=0 => Q=1
  • Q=1 => S=0, R=1 => Q=0

J	K	Q前		S	R		Q	Q#	動作
0	0	0		0	0		0	1	記憶保持
0	0	1		0	0		1	0	記憶保持
1	0	0		1	0		1	0	セット
1	0	1		0	0		1	0	セット
0	1	0		0	0		0	1	リセット
0	1	1		0	1		0	1	リセット
1	1	0		1	0		1	0	反転
1	1	1		0	1		0	1	反転

Dフリップフロップ

• D=1 が入力されると、1を記憶しつつ、1を出力
• D=0 が入力されると、0を記憶しつつ、0を出力

D	Q前		S	R		Q	Q#	動作
0	0		0	1		0	1	リセット
0	1		0	1		0	1	リセット
1	0		1	0		1	0	セット
1	1		1	0		1	0	セット

Tフリップフロップ

T=1 が入力されるたびに、$Q, \overline{Q}$ が反転する。

T	Q前		S	R		Q	Q#	動作
0	0		0	0		0	1	記憶保持
0	1		0	0		0	1	記憶保持
1	0		1	0		1	0	反転
1	1		0	1		0	1	反転

使用例

• アップダウンカウンタ

  • Tフリップフロップを多段にすることで、カウントアップ・カウントダウンができる。

  • 上段に接続する場合は、Q => T に接続する

  • T にはクロックを入力する

    • ポジティブエッジトリガはT入力が「L→H」に変化するタイミングで出力が変化
      => カウントダウンになる
    • ネガティブエッジトリガはT入力が「H→L」に変化するタイミングで出力が変化
      => カウントアップになる

  • Tフリップフロップは単体ではない？ので、Dフリップフロップを使う。

    • $\overline{Q}$ を D に接続することで実現できる。