インターネットを日常的に利用する現代人にとって、最も身近な固有ベクトルの応用例は、Googleが検索順位を決定するのに使うアルゴリズム**「ページランク」かもしれません。ページランクという名前はウェブページの重要度を決定することに由来しますが、同時にGoogleの創設者でありページランクの発明者であるラリー・ペイジのファミリーネームにも掛かった洒落になっています。さて、ページランクの「発明」というと最先端の理論が使われているように聞こえますが、実際のところは19世紀のロシア人数学者アンドレイ・マルコフが創始した「マルコフ連鎖」という確率過程の研究成果の応用として理解できます。確率過程とは「確率的に時間変化する現象」の数理モデルのことであり、マルコフ連鎖とはその中の最も基本となるモデルのことです。無記憶性、つまり「未来の状態が現在の状態のみに依存し、過去の状態には依存しない」**ことを仮定しています(※1)。
※1 正確には無記憶性を持つ確率過程のことを「マルコフ過程」と呼び、マルコフ過程の中でも状態が離散の場合を「マルコフ連鎖」と呼びます。無記憶性の仮定によって、マルコフ過程がとても狭い現象しか扱えないように思えるかもしれません。しかし、「1つ前の状態を格納しておくメモリー」を状態変数として追加すれば、「メモリーの現在の状態」を参照することで、無記憶性の仮定に反することなく、実質的には過去の状態に依存したマルコフ過程を作ることができます。同様にして1~n時点前の状態を格納したn個のメモリを用意すれば、いくらでもマルコフ過程に記憶を持たせることができます(n階マルコフ過程)。結局「無記憶性」という言葉はあくまでも数学用語で、常識的な意味での「記憶」とはややかけ離れています。
まずはマルコフ連鎖がどのようなものかをイメージするため、直感的でわかりやすい例を出しましょう。気象連鎖と呼ばれる、毎日の天気の推移を記述した確率モデルです:
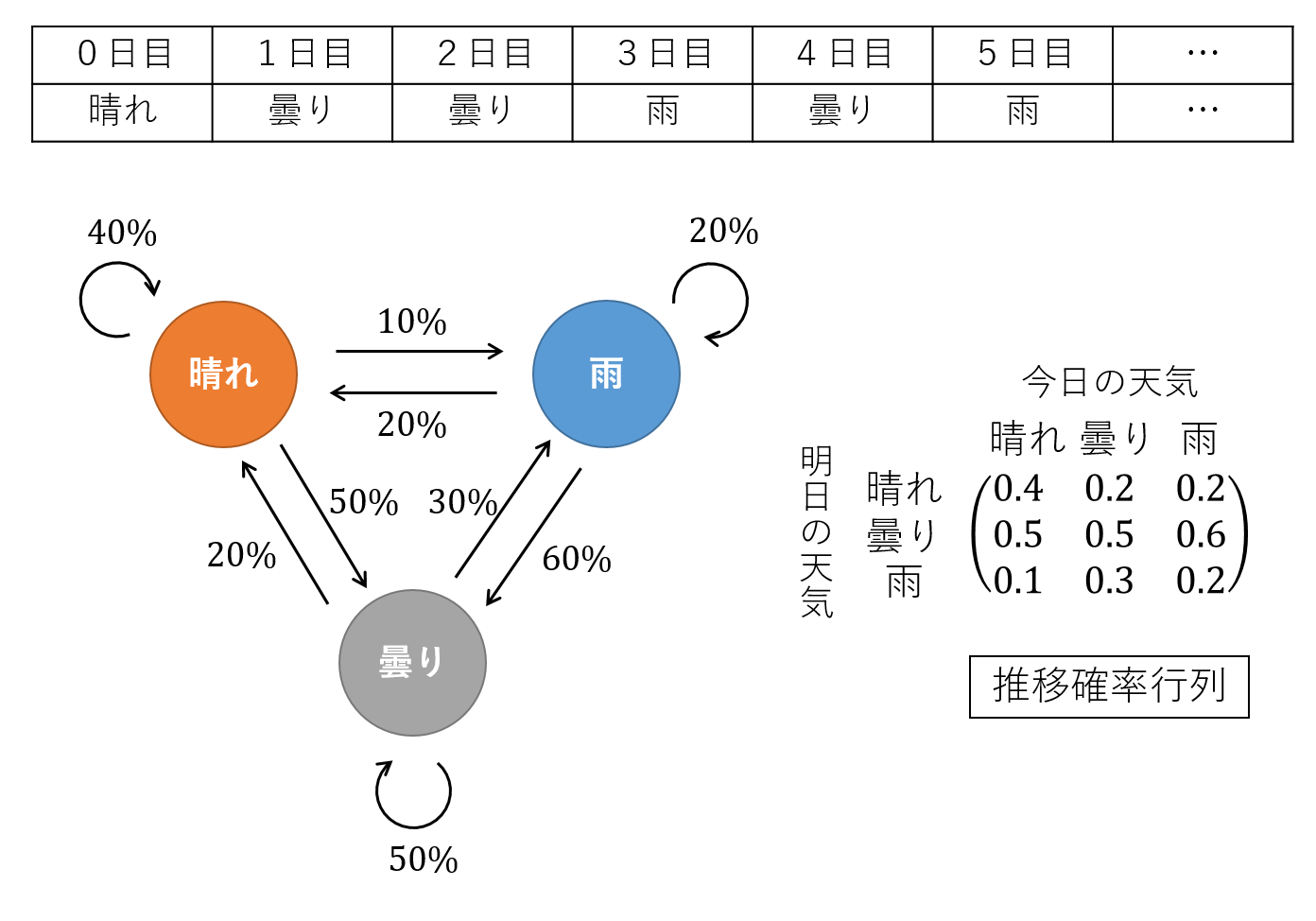
出力したいものは、上の表のような、天気の時系列です。ここでは天気の状態が**「晴れ」「雨」「曇り」の3状態のいずれかしか取らないと仮定しました。このモデルを動かすために設定する必要があるパラメータは、各天気の間を推移する確率だけです。そこで左下の図ように推移確率を設定しました(晴れと雨をダイレクトに行き来する確率より、曇りを経由する確率の方が高い)。この推移確率を、右下のように行列の形でまとめることができます。これを推移確率行列**と呼びます。行列の $(i,j)$ 成分は、今日の天気が $j$ であるときに明日の天気が $i$ になる確率を与えます(※2)。確率なので、すべての成分は非負であり、また列方向(タテ方向)の合計が1です。以上で設定は終わりです。結局、マルコフ連鎖のモデルを作るというのは、推移確率行列を作ることに他なりません。あとは乱数を振って、推移確率の表に従えば、天気の時系列を無限に作ることができます。スゴロクのようなものです。
※2 多くの教科書ではこのiとjを逆に定義しています。その場合、後に述べる時間発展の方法が、「行ベクトル」に対して行列を「右から」作用させることになります。ここでは他の章と同じように「列ベクトルに対して行列を左から作用」させたいため、従来の教科書とは転置する形で定義しました。転置しているだけで本質的な意味は変わりません。
推移確率行列が与えられると、乱数シミュレーションを実際に行わずとも、**確率論的な「天気予報」**をすることができます。今日の天気が「晴れ」だったとして、明日の天気が「晴れ」「曇り」「雨」になる確率はそれぞれ何%でしょうか? 同様に、今日の天気だけがわかっている状態で、明後日、明々後日、そしてn日後の天気が「晴れ」「曇り」「雨」になる確率は何%でしょうか?
マルコフ連鎖における時間発展は、現在の状態の確率分布を表す列ベクトルに推移確率行列を作用することで表現できます。例えば「今日が晴れ」という情報は、「晴れである確率が100%、曇りや雨である確率は0%」ということなので、$ (晴れ, 曇り, 雨)=(1,0,0)$という確率分布のベクトルとして表現できます。このベクトルに推移確率行列を作用させると、明日の天気を表す$(晴れ, 曇り, 雨)$の確率分布のベクトルが得られます。さらに明日の確率分布にもう一度推移確率行列を作用させれば、今度は明後日の確率分布が得られます。同様にして、行列をn回かければ、n日後の天気の確率分布が得られるわけです。
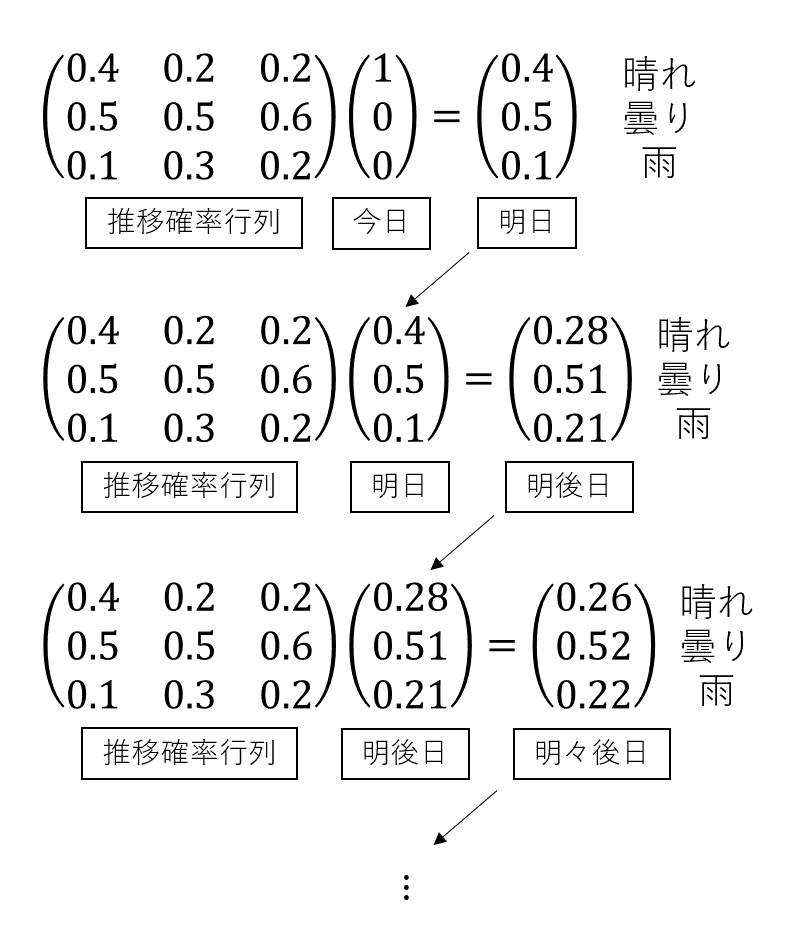
では、100日後の天気予報をしたい場合、用意した初期分布に対して正確に100回行列をかけなければならないのでしょうか? ここで、多くのマルコフ連鎖で使える非常に有用な性質を使いましょう:「充分に長い時間が経ったとき、確率分布は初期状態に依存せず、ある特定の分布に収束する(※3)」。収束する先の確率分布を定常分布と呼びます。定常分布に推移確率行列をかけると、同じ定常分布が得られます。つまり、十分に時間が経ったとき、確率分布が時間的に変化しなくなるのです。
※3 すべてのマルコフ連鎖がこのような性質を持つわけではないものの、マルコフ連鎖が非周期的(大雑把に言えば、同じ状態に留まれること)・正再帰的(有限時間で元の状態に戻れること)・既約(すべての状態が行き来可能であること)であれば、この性質が保証されます。「非周期的・正再帰的・既約」であることをまとめて「エルゴード的」と呼びます(統計力学に由来する)。難しく聞こえますが、エルゴード的なマルコフ連鎖は珍しいものではありません

このような性質を持つベクトルのことを我々は知っています。そう、固有ベクトルです。しかも、確率分布のベクトルは成分の合計が1でなければならないので、固有値は1でなければなりません。言い換えると定常分布とは、推移確率行列が持つ固有ベクトルのうち、固有値が1であるもののことです(そのような固有値と固有ベクトルの組が唯一存在することを保証するペロン・フロベニウスの定理というものがあります)。結局、十分に時間が経った後の確率分布を得るためには、初期状態についてあれこれ考えたり、正確にn回推移確率行列をかける必要はなくて、単に推移確率行列の固有ベクトルを求めればよいのです。
とはいえ、大きい行列に関しては固有値方程式を代数的に解くことが難しいため、結局は何度も行列の掛け算を行って固有ベクトルに収束させるのが普通です。どんな初期値であろうと同じ定常分布に収束することが保障されます。上に示した気象連鎖の例でも、3回行列を掛けただけでかなり定常分布に近付いています。
マルコフ連鎖と定常分布の説明が終わったので、ページランクの説明をする準備が整いました。一言でいうとページランクとは、「ネットサーフィンする人の挙動を表現したマルコフ連鎖の定常分布」のことです。このマルコフ連鎖のことをランダムサーファー・モデルと呼びます(※4)。つまりページランクとは、**「人がそれぞれのウェブページに滞在している確率の分布」**であると解釈できます。それをウェブページの重要度だと考え、検索順位を決定する指標として使っているわけです。さて、以下ではランダムサーファー・モデルの設定を段階的に説明をしましょう。
※4 ちなみに、ページランクの最初の論文にはマルコフ連鎖という言葉は出てきません。ランダムサーファー・モデルというものは、後付けされた方便のようです。
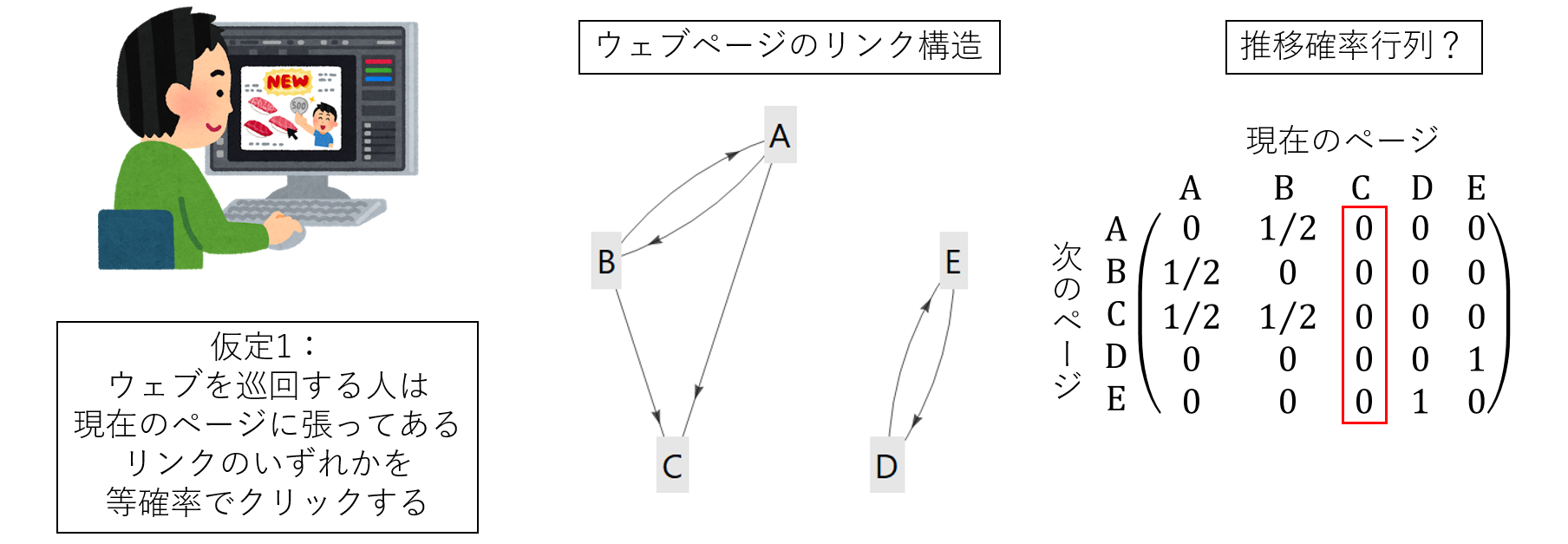
ランダムサーファー・モデルの基本的な考えはとても単純なものです:「ネットサーフィンをしている人は、現在見ているウェブページからリンクされている別のページのいずれかに、均等な確率で飛ぶ(仮定1)」。それぞれのウェブページのコンテンツが何かということはまったく考えず、リンク構造にだけ注目しようというわけです。この仮定から、ウェブページのリンク構造さえわかっていれば推移確率行列を構成できそうです。
しかしここで問題が生じます。上の図に示したウェブページCのように、どこにもリンクを張っていないウェブページだってあります。このようなページがあっては、ちゃんとした推移確率行列を構成することができません。いずれの列の合計も1でなければならないのに、成分がすべてゼロの列が現れてしまうからです。
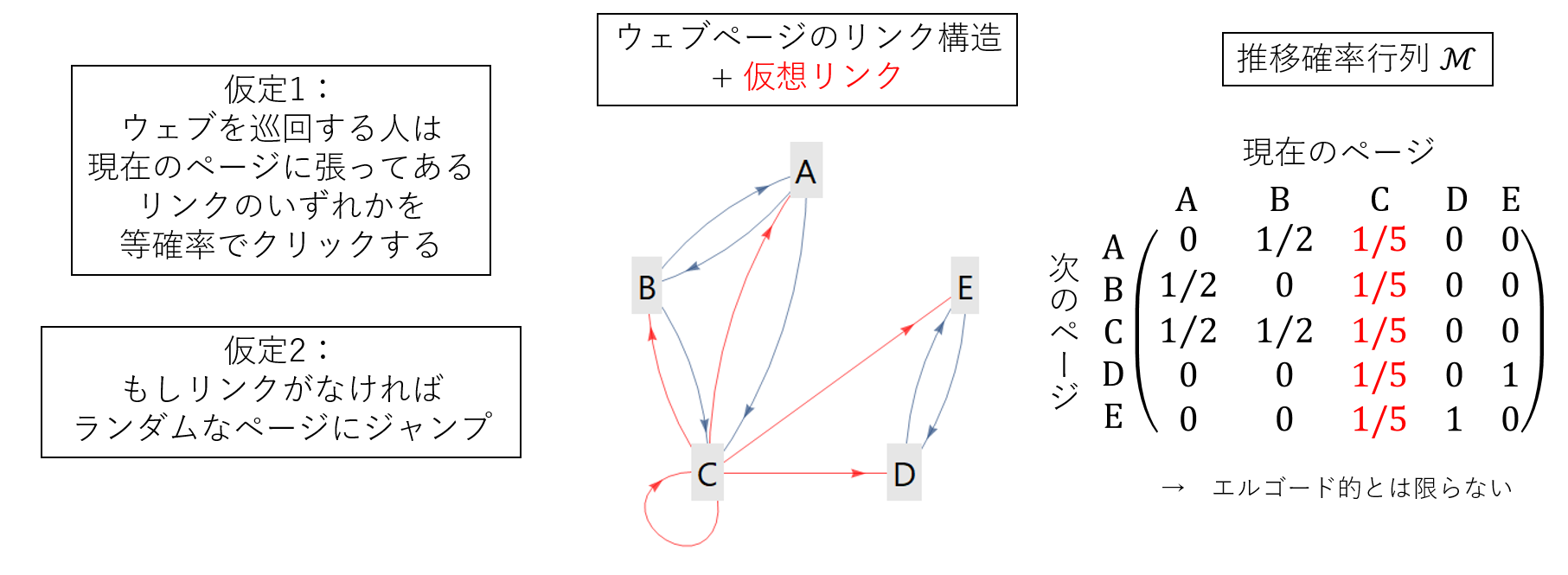
そこで次のような仮定を導入しましょう:「もしも現在のページがどこへもリンクを張っていないなら、全ページのうちいずれかのページに均等な確率でジャンプする(仮定2)」。リンクが張ってないからといって、ネットサーフィンをする人がネットサーフィンをやめるわけではありません。ブックマークから飛ぶなり、URLを直接打ち込むなりして、どこかのページに行くでしょう。ここでは細かいプロセスについては考えず、とりあえず全ページのうちどれかにランダムに飛ぶ、ということにしてしまいましょう。ひとまずこれで、ちゃんとした推移確率行列を構成できます。これを$\mathcal M$と置きます。
これでマルコフ連鎖としての条件はクリアしたわけですが、実はまだ問題が残っています。上の注釈で述べたように、マルコフ連鎖だからといって定常分布の存在が保障されるわけではありません。エルゴード性という3つの条件を満たさなければならないのでした。特に重要なのは、既約と非周期性です(正再帰性という条件は、状態数が有限のマルコフ連鎖の場合、既約と同義になるので無視して良い)。例えば上の図では、CからDに行くことはできても、DからCに行くことができないため、既約ではありません。また、DかEに一旦落ちれば、あとはDとEを交互に巡るだけになるので、周期的になってしまいます。
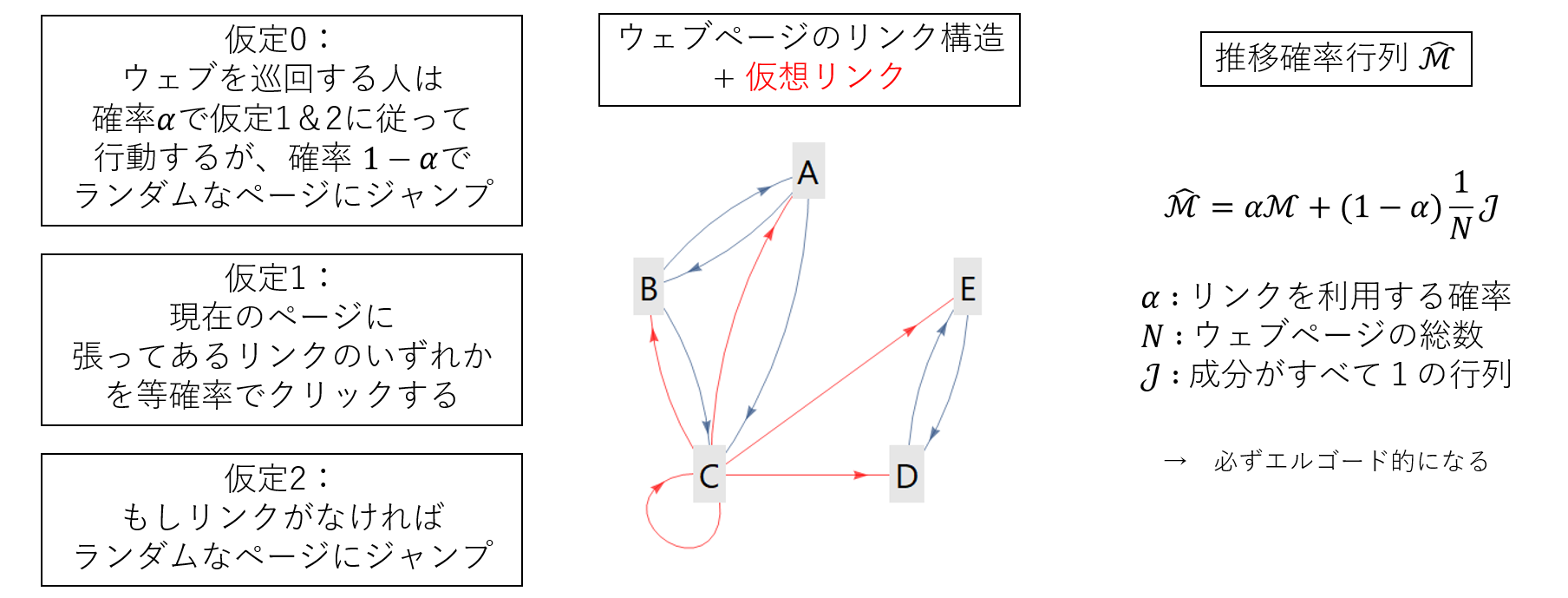
マルコフ連鎖にエルゴード性を満たさせるための手っ取り早い方法は、**「すべての状態を行き来できるようにする」「現在の状態に留まる確率を正にする」**ことです。
そこで、モデルに根本的な修正を加えます:「ネットサーフィンをする人は、そもそもリンク構造を使わずに、全ページのどれかにランダムにジャンプすることもある(仮定0)」。ここで新たなパラメータ$\alpha$を導入し、リンク構造を使う確率を$\alpha$、使わない確率を$1-\alpha$としました。先ほど構成した推移確率行列に$\alpha$をかけ、それとは別に用意した一様な推移確率行列$(1/N)\mathcal J$に$1-\alpha$をかけ、両者を足しあわせれば、目的の新たな推移確率行列$\hat{\mathcal M}$が得られます。これはGoogle行列と呼ばれます。そしてGoogle行列の固有ベクトルが、ページランクになります。
一般的に用いられる$\alpha=0.85$という値を使うと、上の例では、$(A,B,C,D,E)=(0.09,0.09,0.13,0.35,0.35)$という固有ベクトルが得られます。ページランクだけを指標に検索順位を決めるなら、上から順に D or E → C → A or B と表示されることになります(実際のところは、Googleは検索順位を決めるために200近くの指標を用いており、ページランクはそのうちの1つに過ぎないらしいです)。
最後にせっかくですので、ページランク以外にもマルコフ連鎖の応用例を紹介しておきます。ネット関連でいえば、圧縮新聞やしゅうまい君などに代表されるツイッターbotは、自然言語処理における形態素解析と組み合わせたマルコフ連鎖です。状態を直接観測できない場合の隠れマルコフモデル、強化学習の基礎となるマルコフ決定過程、ベイズ推定で使われるMCMC(マルコフ連鎖モンテカルロ法)などもよく使われます。また、マルコフ連鎖とよく似ている概念として、年齢別人口動態のモデルであるレスリー行列というものがあり、この行列の固有ベクトルは**安定齢構成(定常状態の人口ピラミッド)**として、生態学において重要な役割を占めています。