本記事は、私の記事【Python】混合ガウスモデルを使ったクラスタリングの実装の続編になります。
機械学習プロフェッショナルシリーズ『ノンパラメトリックベイズ 点過程と統計的機械学習の数理』を読んで、本に書いてあるモデルをPythonで実装してみました。今回は、前回実装したモデルを改良し、周辺化ギブスサンプリングでクラスタリングを行います。
環境
Python: 3.7.5 numpy: 1.18.1 pandas: 0.25.3 matplotlib: 3.1.2 seaborn: 0.9.0本記事で使われている記号
本記事で使用されている数学的記号のうち、他ではあまり見られないものを説明しておきます。
- $x_{1:N}$ : $x_1, \cdots, x_N$の略
- $x_{1:N}^{\backslash i}$ : $x_{1:N}$から$x_i$を除外したもの
また、本記事におけるベクトルは列ベクトルとし、太字で表記しません。
ギブスサンプリングの復習
周辺化の話の前に、前回のギブスサンプリングをもう少し詳しく説明しなおします。
前回やったことは、データセット$x_{1: N}$がクラスタ$K$個の混合ガウスモデルで表現されると仮定し、各クラスタに対応するガウス分布の平均$\mu_{1:K}$と各データのクラスタ$z_{1: N}$を推定することでした。
$z_{1:N}$と$\mu_{1:K}$の同時分布は次の条件付き確率になりますが、これを解析的に扱うのは困難です。
P(\mu_{1: K}, z_{1:N} | x_{1: N}, \Sigma_{1: K}, \pi)
上式の$\Sigma_{1:K}$はガウス分布の共分散行列、$\pi:=(\pi_1, \cdots, \pi_K)^T$は、各$z_i$が従うカテゴリカル分布のパラメータです。1
そこで、$\mu_{1: K}, z_{1:N}$を同時に推定するのではなく、各変数$\mu_1, \cdots, \mu_K, z_1, \cdots, z_N$を一つづつ順次サンプリングし、これを繰り返すことで全体の推定を行います。この手法をギブスサンプリングといいます。
よって、次の2ステップで推定することになります。
- 各$k=1, \cdots, K$に対し、$P(\mu_k | \mu_{1:K}^{\backslash k}, z_{1:N}, x_{1:N}, \Sigma_{1:K}, \pi, \mu_{\rm pri}, \Sigma_{\rm pri})$をもとに$\mu_k$をサンプリング
- 各$i=1, \cdots, N$に対し、$P(z_i | z_{1:N}^{\backslash i}, \mu_{1:K}, x_{1:N}, \Sigma_{1:K}, \pi)$をもとに$z_i$をサンプリング
$\mu_{\rm pri}, \Sigma_{\rm pri}$は$\mu_k$の事前分布のパラメータです。2
周辺化ギブスサンプリングとは
上記のギブスサンプリングにおいて、データのクラスタを推定している部分は2番目のステップであり、1番目のステップはクラスタの計算に必要な補助的なプロセスです。ここで、周辺化という技法を使って、1番目のステップ「$\mu_{1:N}$のサンプリング」をせずにいきなり2番目のステップ「$z_{1: N}$のサンプリング」を行うことを考えます。この手法を周辺化ギブスサンプリングといいます。周辺化ギブスサンプリングでは、次の1ステップを繰り返します。
- 各$i=1, \cdots, N$に対し、$P(z_i | z_{1:N}^{\backslash i}, x_{1:N}, \Sigma_{1:K}, \pi, \mu_{\rm pri}, \Sigma_{\rm pri})$をもとに$z_i$をサンプリング
周辺化ギブスサンプリングでは、$\mu_{1:K}$の分散が大きい場合3でも、不安定な$\mu_{1:K}$のサンプリング結果に左右されずに$z_{1:N}$をサンプリングすることができます。
$\mu_{1:K}$がないのにどうやって推定するのかと疑問に持った方もいると思いますが、$\mu_{1:K}$の情報は$z_{1:N}^{\backslash i}, x_{1:N}, \Sigma_{1:K}, \pi, \mu_{\rm pri}, \Sigma_{\rm pri}$が持っているので、これらを使って($\mu_{1:K}$を使わずに)$z_i$を推定するイメージです。
ここで、ギブスサンプリングの話から一旦離れて、周辺化について説明します。
同時分布の周辺化
$x \in X, y \in Y$を連続的な確率変数とし、同時分布$P(x, y)$が分かっているとします。
このとき、次のように積分を使って確率変数を消去することを周辺化といいます。
P(x) = \int_{Y}P(x, y)dy
ベイズの定理を使って右辺を変形し、条件付き確率で書くと次のようになります。同時分布ではなく条件付き確率が分かっているケースでは、こちらの方を使います。
P(x) = \int_{Y}P(x|y)P(y)dy
ちなみに、確率変数$y$が離散的な場合、周辺化の定式化は次のようになります。こちらの方が理解しやすいかもしれません。
P(x) = \sum_{y \in Y}P(x, y) = \sum_{y \in Y}P(x|y)P(y)
ギブスサンプリングへの適用
ギブスサンプリングの話に戻ります。$\mu_{1:K}$なしバージョンの$z_i$の確率分布を求めるために周辺化を行います。$D$は$x_i$や$\mu_k$の次元です。条件付き確率の条件の変数が多いので省略して書いています。
P(z_i=k | \cdots)
= \int_{\mathbb{R}^D} P(z_i=k | \mu_{1:K}, \cdots)P(\mu_{1:K} | \cdots)d\mu_{1:K}
前回同様$\Sigma_k = \sigma_k^2 I_D, \Sigma_{\rm pri} := \sigma_{\rm pri}^2I_D$と仮定してこれを計算すると、次のようになります。4
\begin{align}
P(z_i=k | \cdots)
&\propto \pi_k N\left(x_i | a_k\left(\frac{n_k^{\backslash i}}{\sigma^2}\overline{x_k}^{\backslash i} + \frac{1}{\sigma_{\rm pri}^2} \mu_{\rm pri} \right),
\left( \sigma^2 + a_k \right)I_D\right) \\
a_k &:= \left( \frac{n_k^{\backslash i}}{\sigma^2} + \frac{1}{\sigma_{\rm pri}^2} \right)^{-1}
\end{align}
$n_k^{\backslash i}$は$x_{1: N}$から$x_i$を除いたデータセットのうち、クラスタ$k$に所属するデータの個数、$\overline{x_k}^{\backslash i}$はそれらの平均です。
実装
前回の実装をベースに、周辺化ギブスサンプリングを実装します。前回からの大きな変更点は、次の2つです。
- クラス変数
muを削除(サンプリングしないので不要) -
log_deformed_gaussianメソッドの変更
1つ目は周辺化ギブスサンプリングの核となる発想で、一番重要です。
2つ目について説明します。前回、正規分布の確率密度関数値の比を出すために、クラスタkに依存しない因子を無視して計算していました。前回の数式を再掲します。5
\begin{align}
P(z_i = k | x_{1:N}^{\backslash i}, z_{1:N}^{\backslash i}, \mu_{1:K}, \Sigma_{1:K}, \pi)
&\propto \pi_k \exp\left\{- \frac{1}{2}\log|\Sigma_k| - \frac{1}{2} (x_i - \mu_k)^T\Sigma_k(x_i - \mu_k)\right\} \\
&\propto \pi_k \exp\left\{- \frac{1}{2 \sigma^2}\ \| x_i - \mu_k \|_2^2\right\}
\end{align}
ここで、式のように$- \frac{1}{2}\log|\Sigma_k|$の因子を無視できたのは、$\Sigma_k$がクラスタ$k$に依存しない固定値だったためです。
しかし、今回は$\Sigma_k = (\sigma^2 + a_k )I_D$であり、$a_k$は$k$によって変わるので、この因子を無視できなくなります。よって、今回の計算式は次のようになります。
\begin{align}
P(z_i = k | x_{1:N}^{\backslash i}, z_{1:N}^{\backslash i}, \mu_{1:K}, \Sigma_{1:K}, \pi)
&\propto \pi_k \exp\left\{ \frac{D}{2}\log \sigma_k^2 -\frac{1}{2 \sigma^2}\ \| x_i - \mu_k \|_2^2\right\}
\end{align}
このexpの中身を計算するメソッドlog_deformed_gaussianの実装は次のようになります。
def log_deformed_gaussian(x, mu, var):
D = x.shape[0]
norm_squared = ((x - mu) * (x - mu)).sum(axis=1)
return -D * np.log(var) / 2 - norm_squared / (2 * var)
以上を踏まえて、実装してみました。長いので折りたたみにしています。
ソースコード
import numpy as np
from collections import Counter
def log_deformed_gaussian(x, mu, var):
norm_squared = ((x - mu) * (x - mu)).sum(axis=1)
return -np.log(var) / 2 - norm_squared / (2 * var)
class ClusterArray(object):
def __init__(self, array):
# arrayは1次元のリスト、配列
self._array = np.array(array, dtype=np.int)
self._counter = Counter(array)
@property
def array(self):
return self._array.copy()
def count(self, k):
return self._counter[k]
def __setitem__(self, i, k):
# 実行されるとself._counterも更新される
pre_value = self._array[i]
if pre_value == k:
return
if self._counter[pre_value] > 0:
self._counter[pre_value] -= 1
self._array[i] = k
self._counter[k] += 1
def __getitem__(self, i):
return self._array[i]
# 周辺化ギブスサンプリングでクラスタリングを行うクラス
class GMMClustering(object):
def __init__(self, X, K, var=1, var_pri=1, seed=None):
self.X = X.copy()
self.K = K
self.N = X.shape[0]
self.D = X.shape[1]
self.z = None
# 確率分布のパラメータ設定
# self.muは使わないので定義しない
self.var = var # 固定、すべてのクラスタで共通
self.pi = np.full(self.K, 1 / self.K) # 固定、すべてのクラスタで共通
# 事前分布の設定
self.mu_pri = np.zeros(self.D)
self.var_pri = var_pri
self._random = np.random.RandomState(seed)
def fit(self, n_iter):
init_z = self._random.randint(0, self.K, self.N)
self.z = ClusterArray(init_z)
for _ in range(n_iter):
for i, x_i in enumerate(self.X):
self.z[i] = self._sample_zi(i)
def _sample_zi(self, i):
n_vec = np.array([
self.z.count(k) - bool(k == self.z.array[i])
for k in range(self.K)
])
x_bar_vec = np.array([self._mean_in_removed(k, i) for k in range(self.K)])
tmp = 1/(n_vec/self.var + 1/self.var_pri)
mu = np.tile(tmp, (self.D, 1)).T * (np.tile(n_vec, (self.D, 1)).T * x_bar_vec / self.var + self.mu_pri / self.var_pri)
var = tmp + self.var
log_probs_xi = log_deformed_gaussian(self.X[i], mu, var)
probs_zi = np.exp(log_probs_xi) * self.pi
probs_zi = probs_zi / probs_zi.sum()
z_i = self._random.multinomial(1, probs_zi)
z_i = np.where(z_i)[0][0]
return z_i
def _mean_in_removed(self, k, i):
# self.Xからi番目を抜いたデータセットのうち、クラスタkに所属するデータの平均を計算する
mean = np.array([
x for j, x in enumerate(self.X)
if (j != i) and (self.z[j] == k)
]).mean(axis=0)
return mean
結果
前回同様、アヤメのデータセットに対してクラスタリングを試しました。ハイパパラメータの$\sigma^2=0.1, \sigma_{\rm pri}^2=1$とし、ギブスサンプリングの反復回数を$10$回としています。これらは前回同様の設定です。
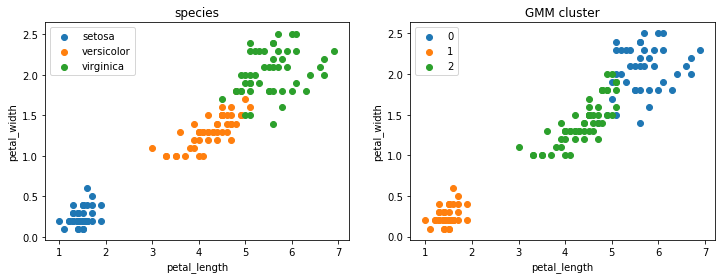
実際のデータセットのラベルとクラスタリング結果を比較すると、次のようになりました。
ソースコード
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
# データセットの読み込み
df = sns.load_dataset('iris')
X = df[['sepal_length', 'sepal_width', 'petal_length', 'petal_width']].values
# 混合ガウスモデルによるクラスタリング
gmc = GMMClustering(X, K=3, var=0.05, seed=1)
gmc.fit(n_iter=10)
df['GMM_cluster'] = gmc.z.array
# 結果の可視化
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
for sp in df['species'].unique():
x = df[df['species'] == sp]['petal_length']
y = df[df['species'] == sp]['petal_width']
ax1.scatter(x, y, label=sp)
ax1.legend()
ax1.set_title('species')
ax1.set_xlabel('petal_length')
ax1.set_ylabel('petal_width')
for k in range(gmc.K):
x = df[df['GMM_cluster'] == k]['petal_length']
y = df[df['GMM_cluster'] == k]['petal_width']
ax2.scatter(x, y, label=k)
ax2.legend()
ax2.set_title('GMM cluster')
ax2.set_xlabel('petal_length')
ax2.set_ylabel('petal_width')
plt.show()
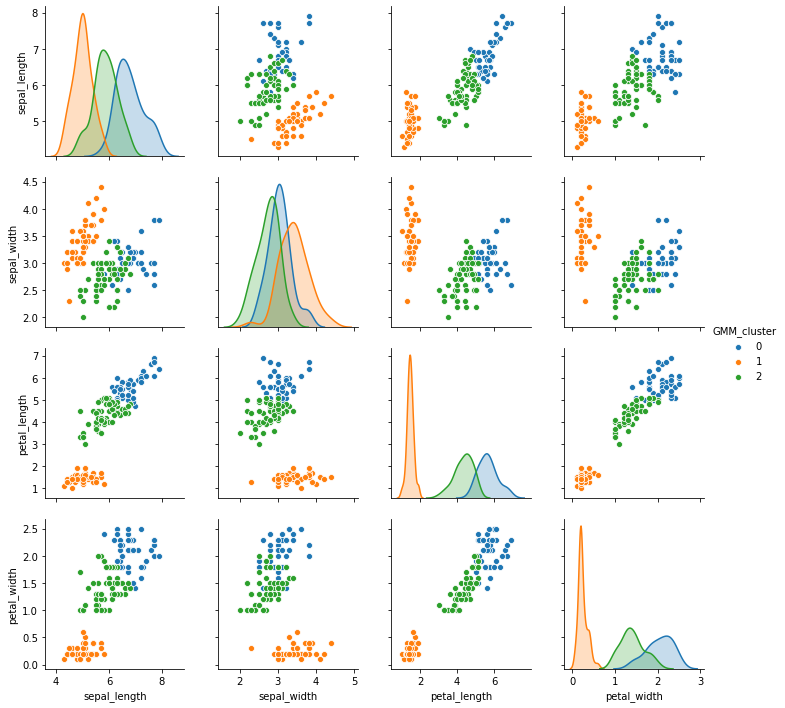
seabornのpairplotを使って結果を可視化すると、次のようになりました。
ソースコード
sns.pairplot(
df.drop(columns=['species']),
vars=['sepal_length', 'sepal_width', 'petal_length', 'petal_width'],
hue='GMM_cluster'
)
$\mu_{1: K}$をサンプリングしない周辺化ギブスサンプリングでも、いい感じにクラスタリングできていますね。
おわりに
機械学習プロフェッショナルシリーズ『ノンパラメトリックベイズ 点過程と統計的機械学習の数理』から、周辺化ギブスサンプリングを実装して、前回と同様のクラスタリングができることを確認しました。
次回は、この本のメインコンテンツであるノンパラメトリックベイズを実装する予定です。
-
前回同様、これらは確率変数とせずに固定値とします。 ↩
-
$\mu_k$の確率分布をベイズ推定するため、事前分布の設定が必要です。 ↩
-
$\mu_k$の分散が大きくなるのは、クラスタ$k$に所属するデータ数が少ない場合です。周辺化ギブスサンプリングでは、極端な例ですが、クラスタ$k$に所属するデータが$0$個であっても$z_i=k$になる確率を求めることができます。ノンパラメトリックベイズでは、この性質が重要になります。 ↩
-
本にはこの導出方法が書いてありますが、自分自身でも計算を確かめました。結構大変でした。 ↩
-
前回は確率分布そのものを記載しましたが、今回は比例式を記載しています。慣れればこっちのほうが分かりやすいと思います。 ↩