はじめに
地磁気センサの簡単な説明と、地磁気センサが示す値に含まれる誤差のうち、
センサが搭載された機体から受ける影響を校正する方法について紹介します。
数式による説明と、c++で書いた更新式の関数、ROS2コンポーネントとしての実装を紹介した後に、9軸センサMPU9250搭載の地磁気センサの実測値から推定した結果を提示しました。
地磁気センサについて
地磁気センサは方位磁針のようなもので、周囲の磁場の方向を測定するセンサです。
磁場の方向と強度を測定し、その結果を2次元または3次元のベクトルとして出力します。
地球の磁場はほぼ北方向を向いており、局所的には強度が一定ですから、
3次元地磁気センサの測定値は球上に分布します。
しかし、磁場を発生する物体は地球だけではなく、そのため外乱の影響を受けやすいセンサでもあります。
MATLABの解説ページによると、センサの誤差は大きく2つに分けて考えることができます。
-
Hard iron effect
センサが搭載された機体から発生する磁場の影響を示したものです。
普通、センサは機体に固定されていますから、センサに対して常に一定方向の磁場が働くことになります。
したがって、センサの測定値に定常値が加算されます。 -
Soft iron effect
壁や電化製品など、機体周辺にある物体の磁場の影響を示したものです。
センサの測定値を歪める効果が有ります。
したがって、地磁気センサから正確な値を得るためには、Hard iron effect と Soft iron effectを補正する必要が有ります。
キャリブレーション方法
前述の通り、Hard iron effectによってセンサの測定値はある点を中心にした球面上に分布すると考えられます。
そこで、球面の中心をセンサデータから推定する方法について球面の方程式から考えます。
式
理論的な部分について簡単に説明します。
とりあえずコードを見せろ!という方は読み飛ばしてください。
センサ値の分布が綺麗な球面状だと仮定すると、センサが示す磁場の方向$(x,y,z)$は球面の方程式(1)で表せます。
(x-x_0)^2+(y-y_0)^2+(z-z_0)^2 = r^2 \tag{1}
ここで、$(x_0,y_0,z_0)$が球面中心の座標を表し、$r$が球の半径を表します。
したがって、キャリブレーションを通じて$(x_0,y_0,z_0)$と$r$を知りたい、ということになります。
この問題に対して、今回は$(x_0,y_0,z_0)$に適当な初期値を与えて、実際のデータを用いて修正するという方法を取りました。
推定開始時点では、$(x_0,y_0,z_0)$の正解が分からないため適当な値を与えますが、
その時点ではこの方程式が成り立ちません。
そこで、各時点で推定される$(x_0,y_0,z_0,r)$を用いて(1)の両辺の差を求めます(2)。
これの2乗は $J\ge0$ で、$(x_0,y_0,z_0,r)$ が正解のとき $J=0$ になります。
\epsilon = (x-x_0)^2+(y-y_0)^2+(z-z_0)^2 - r^2 \tag{2}
J=\epsilon^2 \tag{3}
$J$が小さくなるように$x_0,y_0,z_0,r$を更新したいので、次のような更新式を定義します。
\begin{eqnarray}
x_{0,n+1} &=& x_{0,n} - \mu \frac{\partial{J}}{\partial{x_0}} = x_{0,n} + 4\mu\epsilon(x-x_0) \\
y_{0,n+1} &=& y_{0,n} - \mu \frac{\partial{J}}{\partial{y_0}} = y_{0,n} + 4\mu\epsilon(y-y_0)\\
z_{0,n+1} &=& z_{0,n} - \mu \frac{\partial{J}}{\partial{z_0}} = z_{0,n} + 4\mu\epsilon(z-z_0)\\
r_{n+1} &=& r_{n} - \mu \frac{\partial{J}}{\partial{r}} = r_{n} - 4\mu\epsilon{r}
\end{eqnarray} \tag{4}
$\mu$ は更新の利きを調整するものです。学習率やゲイン、利得などと呼ばれます。
大きすぎると計算がうまくいかず、小さすぎると必要な計算回数が大きくなります。
式にある $\partial{J}/\partial{*}$ は偏微分というもので、$*$の変化と$J$の変化の関係性を表します。
$\partial{J}/\partial{*}\ge0$ であれば、「$x$が増加すると$J$も増加する」を意味して、$\partial{J}/\partial{*}\le0$ であればその逆です。
$\partial{J}/\partial{x_0}$は$x_0$以外の文字を定数とみなして、$J$を$x_0$で微分することによって得られます。
\begin{eqnarray}
\frac{\partial{J}}{\partial{x_0}}&=&-4\epsilon(x-x_0)\\
\frac{\partial{J}}{\partial{y_0}}&=&-4\epsilon(y-y_0)\\
\frac{\partial{J}}{\partial{z_0}}&=&-4\epsilon(z-z_0)\\
\frac{\partial{J}}{\partial{r}}&=&-4\epsilon{r}
\end{eqnarray} \tag{5}
今回は $J$ を減少させたいので、$-\partial{J}/\partial{*}$ によって更新します。
コード
前項に紹介した(4)式をコードにすると、次の関数にまとめられます。
測定データを保持する必要が無いために、メモリ制約ある組み込み系にも使いやすいのではないでしょうか。
double b[4]; // 推定対象[x_0, y_0, z_0, r]
double dx, dy, dz, f;
void update(double x, double y, double z)
{
dx = x - b[0];
dy = y - b[1];
dz = z - b[2];
f = dx*dx + dy*dy + dz*dz - b[3]*b[3];
b[0] = b[0] + 4 * lr * f * dx;
b[1] = b[1] + 4 * lr * f * dy;
b[2] = b[2] + 4 * lr * f * dz;
b[3] = b[3] + 4 * lr * f * b[3];
}
実装例
ここでは、上記の関数を実装したROS2コンポーネントを作成し、地磁気センサの測定値から校正値を推定してみました。
ROS(Robot Operating System)はロボット向けのOS(むしろ通信プロトコル?)で、
マイコンとPCの情報のやり取りをUSBやWiFi経由で行うことができます。
以下に、C++コードによる実装と実際の推定結果について紹介します。
環境
ROS2によるPCとESP32の接続に関しては以前に紹介しました。今回は省略します。
(マイコン側)
- ESP-WROOM-32
- MPU9250
- ros2arduino
(PC側)
- Ubuntu 18.04
ROS2コンポーネントによる実装
ROSはトピック通信という方法でマイコンやPCが相互に情報を送受信します。
ここでは、"/sensor/magnetic_field"というトピックで実機から送信される地磁気センサの測定値をPCで受信して、PC上で推定を行いました。
また、地磁気センサの測定値はWiFiに接続されたESP32から取得しました。
地磁気センサ -(I2C通信)-> ESP32 -ROS2・WiFi(UDP)-> PC(Ubuntu):推定
ヘッダファイル
ヘッダファイルはこちらです。
(4)式との対応についてですが、lrが$\mu$、bが$[x_0,y_0,z_0,r]$、fが$\epsilon$ です。
ROS2のノードの形式になっていますが、要はクラスなので、rclcpp::~となっている部分を消せば他のプログラムにも利用できると思います。
# include "rclcpp/rclcpp.hpp"
# include <geometry_msgs/msg/vector3.hpp>
namespace calibration
{
class Magnetometer : public rclcpp::Node
{
private:
double lr; // learning rate
double b[4]; // bias: [x, y, z, r]
double f; // residual = (xi-x)^2 + (yi-y)^2 + (zi-z)^2 - r^2
double dx, dy, dz; //
public:
explicit Magnetometer (const rclcpp::NodeOptions & options);
virtual ~Magnetometer (){}; // TODO: Destructor
rclcpp::Subscription<geometry_msgs::msg::Vector3>::SharedPtr sub_sensor_magn;
void sub_magn_callback(const geometry_msgs::msg::Vector3::SharedPtr msg);
void update(double x, double y, double z);
double *get_bias();
};
}
ソースファイル
次に、ソースファイルです。センサの測定値を受信するとsub_magn_callbackが呼び出され、上述のupdate関数が実行される仕組みです。
推定する$(x_0,y_0,z_0)$の初期値は $0$ とし、 $r$ は$1$としました。
これは、理想的には求める球の中心は原点に位置するためです。$r$は適当ですが、日本の地磁気の大きさは46,000nT前後らしいので、それに対応する値を入れる方が良いかもしれません。
# include "rclcpp/rclcpp.hpp"
# include <geometry_msgs/msg/vector3.hpp>
# include "communicator/magnetometer_calibration.hpp"
using std::placeholders::_1;
# include <iostream>
# include <fstream>
using namespace std;
calibration::Magnetometer::Magnetometer(const rclcpp::NodeOptions & options) : Node("Magnetometer", options)
{
lr = 0.00001;
for (size_t i = 0; i < 3; i++) {
b[i] = 0.0;
}
b[3] = 1.0;
f = 0.0;
dx = 0.0;
dy = 0.0;
dz = 0.0;
sub_sensor_magn = this -> create_subscription<geometry_msgs::msg::Vector3>(
"/sensor/magnetic_field",
rclcpp::QoS(1).best_effort().durability_volatile(),
std::bind(&Magnetometer::sub_magn_callback, this, _1)
);
ofstream outputfile("magnetometer_calib.csv", ios::app);
outputfile << "mx, my, mz, x0, y0, z0, r" << endl;
outputfile.close();
}
void calibration::Magnetometer::sub_magn_callback(const geometry_msgs::msg::Vector3::SharedPtr msg)
{
RCLCPP_INFO(this->get_logger(), "Magn: [%.2f, %.2f, %.2f]", msg->x, msg->y, msg->z);
calibration::Magnetometer::update(msg->x, msg->y, msg->z);
RCLCPP_INFO(this->get_logger(), "sub_calib: [%.2f, %.2f, %.2f, %.2f]", b[0], b[1], b[2], b[3]);
ofstream outputfile("magnetometer_calib.csv", ios::out | ios::app);
outputfile << msg->x << ",";
outputfile << msg->y << ",";
outputfile << msg->z << ",";
outputfile << b[0] << ",";
outputfile << b[1] << ",";
outputfile << b[2] << ",";
outputfile << b[3] << endl;
outputfile.close();
}
void calibration::Magnetometer::update(double x, double y, double z)
{
dx = x - b[0];
dy = y - b[1];
dz = z - b[2];
f = dx*dx + dy*dy + dz*dz - b[3]*b[3];
b[0] = b[0] + 4 * lr * f * dx;
b[1] = b[1] + 4 * lr * f * dy;
b[2] = b[2] + 4 * lr * f * dz;
b[3] = b[3] + 4 * lr * f * b[3];
}
double* calibration::Magnetometer::get_bias()
{
return b;
}
# include "rclcpp_components/register_node_macro.hpp"
RCLCPP_COMPONENTS_REGISTER_NODE(calibration::Magnetometer)
結果
最後に、推定結果について説明します。
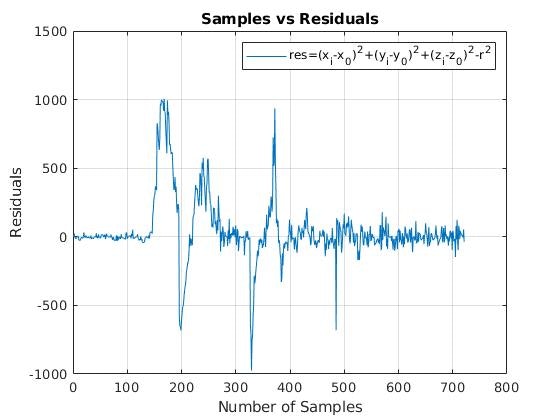
まず、(3)式の $\epsilon$ を用いて、推定値の精度について示したものが下の図です。約100サンプル目からセンサを8の字状に動かしました。
はじめは $\epsilon$ が大きく動いていることから、正確に中心が得られていないことがわかります。
サンプルの増加に従い、 $\epsilon$ の大きさが小さくなり、400サンプル程度で0付近に収束しました。
センサを8の字状に動かすことで、センサ視点での磁場の方向が変化しますから、あらゆる磁場方向に対して $\epsilon$ が小さくなっていると解釈できます。
したがって、測定値がなす球面の中心を推定できたと考えられます。
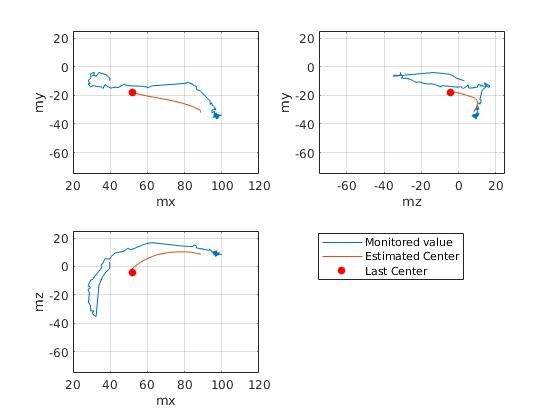
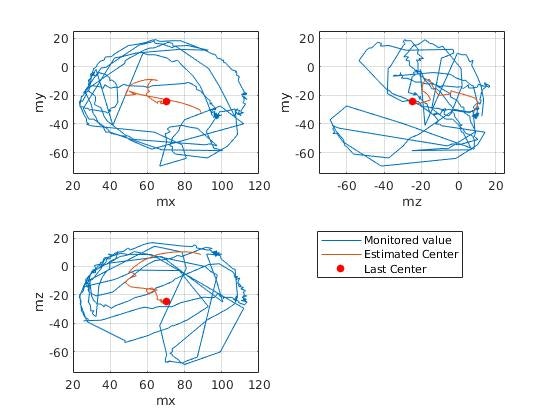
次に、測定データと球の中心の推定値について時系列変化を紹介します。
200サンプル目の時点では、センサの値は球全体のごく一部に限られています。
したがって、推定も得られたデータのみで行われており、精度は高くありません。
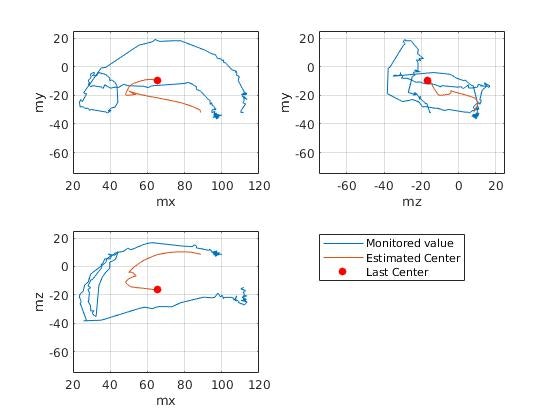
次に300サンプル目です。
この時点で、半円状の測定データが得られており、人の目にも球の中心がおよそ想像できるのではないでしょうか。
推定値に関しても、半円状の軌跡が明確に見られるx軸・y軸成分に関しては、球の中心に近い部分を取るようになりました。
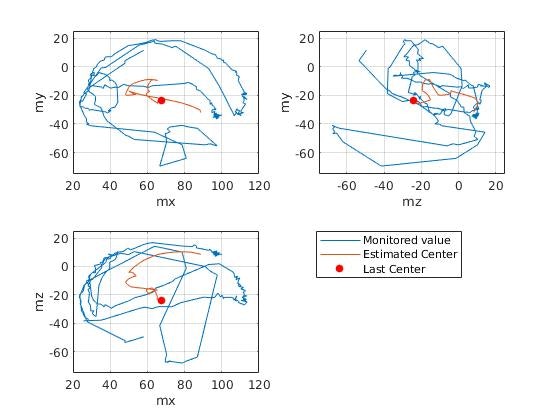
400サンプル目の時点では、z軸成分についても円上の軌跡が描かれるようになり、中心に近づきました。
500サンプル目の時点では、400サンプル目の時点との推定値変化が小さくなりました。
最初に示した $\epsilon$ の変化とも併せて考えると、球面の中心に推定値が収束がしたと考えられます。
まとめ
地磁気センサのキャリブレーション方法について簡単な数式とC++での実装を紹介しました。
球面の方程式から得られる式を用いて球面の推定を行うことで、校正値を得ることができました。
MPU9250は電子工作でよく使われるセンサだと思いますが、地磁気センサのキャリブレーションに関しては意外と情報が少ななかったので、ここで紹介してみました。
※ 私自身も勉強中の身です。些細なことでもコメント・ご意見ください!