環境
- Windows 10
- Python 3.7
- pypeR 1.1.2
- R 3.5.1
- anovakun_482
モチベーション
2要因混合計画の分散分析がしたい。
Scikit-learnとかMNEとか使っているので、もうすべての解析をPythonでやってしまいたい。
Pythonで2元配置のANOVAをやるとなると、statsmodelsっていうモジュールを使って、モデル式を書いてやればいいらしい
(モデル式自体は、このあたり見ればわかりそう)。
そしてその後下位検定、あ、その前に球面性検定もしなくちゃならないんだったかな…
久しぶりで忘れてしまっている。
あーめんどくさい。
RだったらANOVA君使って一発なのに。
そうだ、PythonでANOVA君を動かそう。
必要なものを揃える
サンプルデータセット
とりあえず、解析を試してみる用のデータセットが欲しい。
オープンなデータセットでも引っ張ってこようかと思ったけれど、その方法を調べたり、適切なデータセット探したりするのに時間がかかりそうなので、適当に自作。
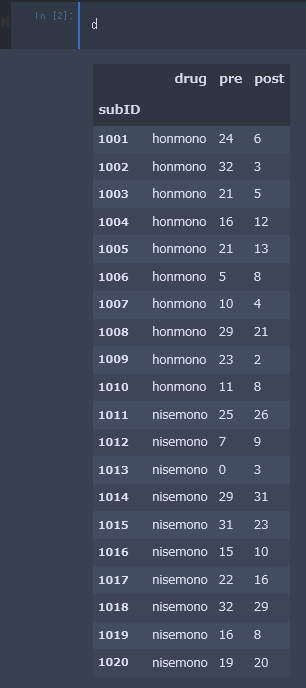
こちらからダウンロード可能です。
設定としては、抑うつっぽい患者を集め、2群に分ける。
一方の群には抗うつ剤(本物)、もう一方には、プラセボ(偽物)を投与。
投与前(pre)と投与後(post)で抑うつ重症度を測定。
交互作用を見ることで、抗うつ剤はプラセボと比べてもちゃんと効果を持っていることを確認、というもの。
これに対し、2(時期:投薬前・後)x2(薬種類:本物・偽物)混合計画(時期だけ被験者内繰り返し)分散分析を行う。
ひとまず、test_anovakun.csvという名前で、デスクトップへ置いておく。
PythonからRを呼び出すモジュール
「PythonでR」でググると、PythonとRで連携するという記事が見つかった。
pypeRというものを使えばいいらしい。
パイプアールと読むのかしらん。
とりあえず、pip。
pip install pyper
その他のPythonモジュール
データの取り扱いのために、numpyとpandasを使います。
持っていない人は、pipで今すぐゲット!
pip install numpy pandas
なおここでは、解析の環境としてjupyter notebookを使います。
統計ソフトR
当然ながら、Rを別でインストールする必要があるらしい。
サイトからダウンロードしてインストール。

(なにこの顔文字)
インストーラーの指示どおりにインストールします。
ANOVA君
Rで動作する分散分析のための関数。
井関龍太先生のHPからコードの書かれたtxtファイルをダウンロードします。
これもひとまず、デスクトップへ置いておきます。
ANOVA君実行
データフレーム作成
先ほど用意したcsvファイルをpandasで読み込み、データフレームを作ります。
import pandas as pd
d = pd.read_csv('test_anovakun.csv', index_col=0)
(カレントディレクトリはデスクトップにしてあります)
Rにデータを渡す
まず、Rをインスタンスとして立ち上げる。
import pyper
r = pyper.R(use_pandas='True')
しかし実行してみると、
FileNotFoundError: [WinError 2] 指定されたファイルが見つかりません。
とエラーが出てしまう。
Rのあるパスが認識されていないのかな?
このあたりを参考にPATHの設定を行ってみましたが、うまくいきませんでした。
結局のところ、ここを参考に、Rのあるパスを入力してやることでうまくいきました。
r = pyper.R(use_pandas='True', RCMD='C:\\Program Files\\R\\R-3.5.1\\bin\\x64\\R')
ちょっとめんどくさい。
もっといい方法はありそうだけれど、とりあえずこれでヨシとする。
このインスタンスに、先ほどのpandasデータフレームを渡します。
r.assign('d', d)
'd'は、Rにおける変数名で、自由に設定してOKです。
Rの中のdに、Python上の変数であるdを渡すわけです。
ANOVA君を走らせる
初めに、RにANOVA君の関数を読み込ませます。
r('source(file="anovakun_482.txt")')
いよいよ、ANOVA君をR内で実行させます。
今回であれば、下記のコードでいけます。
result = r('anovakun(d, "AsB", 2, 2)')
print(result)
ANOVA君では、要因計画の型と、各要因の水準数を引数に入力します。
"AsB"は、要因がAとBの二つであることを示しています。
sで区切られていますが、sの左にあるアルファベットは被験者間要因、右にあるアルファベットは被験者内要因であることを示しています。
例えば今回のデータでは、「時期(投薬前・後)」と「薬種類(本物・偽物)」の2要因です。
"AsB"のうちAは被験者間要因ですので「薬種類」、Bは被験者内要因ですので「時期」になります。
もし被験者間2要因計画でしたら"ABs"となりますし、被験者内2要因計画でしたら"sAB"が、引数の中身となります。
今回のデータでは、AもBも2水準ですので、続いての引数は 2, 2 となります。
その他、いろいろとオプションを付けることができます。
詳しくはANOVA君関数の頭に記載されています。
上記コードを実行すると、結果がだーっと表示されるはずです。
ANOVA君の結果を読み解く
しばらくANOVAやってないと、統計の話が頭から抜けてしまっていてよくないですね。
ANOVAの結果を復習しながら見ていきます。
<< DESCRIPTIVE STATISTICS >>
--------------------------------
A B n Mean S.D.
--------------------------------
a1 b1 10 19.2000 8.6127
a1 b2 10 8.2000 5.7697
a2 b1 10 19.6000 10.4584
a2 b2 10 17.5000 9.7439
--------------------------------
初めに、記述統計量が表示されます。
Aは被験者間計画なので、「薬種類」です。
a1は「本物」ですね。
Bは被験者内ですので、「時期」です。
b1が「投薬前」となります。
つまり1行目は、「本物」の群で、「投薬前」におけるデータ数は10、平均値は19.2、標準偏差は8.6127ということになります。
<< SPHERICITY INDICES >>
== Mendoza's Multisample Sphericity Test and Epsilons ==
-------------------------------------------------------------------------
Effect Lambda approx.Chi df p LB GG HF CM
-------------------------------------------------------------------------
B 0.0747 4.9007 1 0.0268 * 1.0000 1.0000 1.0000 1.0000
-------------------------------------------------------------------------
LB = lower.bound, GG = Greenhouse-Geisser
HF = Huynh-Feldt-Lecoutre, CM = Chi-Muller
球面性検定の結果です。
被験者内要因を含むANOVAをする前提として、すべての条件間の差の分散が等しいことを確認します。
が、今回は被験者内要因が2水準なので関係ありません(そうだったそうだった)。
<< ANOVA TABLE >>
------------------------------------------------------------
Source SS df MS F-ratio p-value
------------------------------------------------------------
A 235.2250 1 235.2250 1.8452 0.1911 ns
s x A 2294.6500 18 127.4806
------------------------------------------------------------
B 429.0250 1 429.0250 15.0991 0.0011 **
A x B 198.0250 1 198.0250 6.9693 0.0166 *
s x A x B 511.4500 18 28.4139
------------------------------------------------------------
Total 3668.3750 39 94.0609
+p < .10, *p < .05, **p < .01, ***p < .001
こちらがANOVAの結果ですね。
Bの行が有意になっているので、時期の主効果あり。
AxBの行が有意になっているので、交互作用ありです。
<< POST ANALYSES >>
< SIMPLE EFFECTS for "A x B" INTERACTION >
-----------------------------------------------------------------------
Effect Lambda approx.Chi df p LB GG HF CM
-----------------------------------------------------------------------
B at a1 1.0000 -0.0000 0 1.0000 1.0000 1.0000 1.0000
B at a2 1.0000 -0.0000 0 1.0000 1.0000 1.0000 1.0000
-----------------------------------------------------------------------
LB = lower.bound, GG = Greenhouse-Geisser
HF = Huynh-Feldt-Lecoutre, CM = Chi-Muller
--------------------------------------------------------------
Source SS df MS F-ratio p-value
--------------------------------------------------------------
A at b1 0.8000 1 0.8000 0.0087 0.9266 ns
Er at b1 1652.0000 18 91.7778
--------------------------------------------------------------
A at b2 432.4500 1 432.4500 6.7447 0.0182 *
Er at b2 1154.1000 18 64.1167
--------------------------------------------------------------
B at a1 605.0000 1 605.0000 12.8118 0.0059 **
s x B at a1 425.0000 9 47.2222
--------------------------------------------------------------
B at a2 22.0500 1 22.0500 2.2955 0.1640 ns
s x B at a2 86.4500 9 9.6056
--------------------------------------------------------------
+p < .10, *p < .05, **p < .01, ***p < .001
自動で多重比較をやってくれた結果です。
A at b2が有意になっています。
つまり、投薬後における得点が、薬種類によって異なるということです。
また、B at a1が有意になっています。
これは、薬種類が本物の場合、投薬前後の得点に有意差があるということです。
仮説通りの結果になりました。
Pythonにデータを返す
ここまでで、やりたいことはおおむね完遂できました。
しかし、出てきた結果を一回Pythonに返してもらいたい時もあります。
そんなときは、こうします。
result = r.get('anovakun(d, "AsB", 2, 2, tech=T)')
ポイントは2点です。
まず、ANOVA君にtech=Tの引数を与えてやることです。
これによってANOVA君は、結果出力を文章でなく、複数のデータフレームをリストで繋いだ形で行ってくれます。
その出力された変数をr.get()で拾い上げます。
これによって、変数resultには、辞書型でデータが返されます。
どんなデータがresultに含まれるかを確認するには、result.keys()です。
下記のような答えが返ってくるはずです。
dict_keys(['INFORMATION', 'DESCRIPTIVE STATISTICS', 'SPHERICITY INDICES', 'ANOVA TABLE', 'POST ANALYSES'])
ここで例えばANOVA TABLEの情報を読み出したければ、下記のようにします。
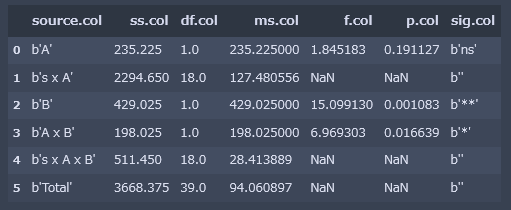
result['ANOVA TABLE'][1]
(なぜ[1]なのかよくわかりません。[0]と[2]にはNoneが入っています)
これで、下記のように、pandas.DataFrame形式でデータが返されるはずです。
まとめ
PythonからRを使えるという話は前から聞いていました。
便利そうだなーと思いつつ、大体はscipyで片付いてしまっていました。
しかしこの技術によって、ANOVA君という神関数をPythonへ引き込むことができました。