はじめに
この記事は$\TeX$とMarkdown記法の練習と部活の講習をするために書きました。そのため厳密な表現ではない部分や誤りなどがあるかもしれません。すいません。
メカナムホイールとは?
メカナムホイールとは次の画像のように車輪円周上に45度の角度でローラーが取り付けられているホイールのことです。

このようなホイールが4輪ロボットの対角線上に配置されています。
このホイールの最も大きな特徴として全方向移動が可能ということがあります。それぞれのホイールを回転する速度を調節することで対向2輪型ロボットでは不可能な左右移動をすることができます。しかし、対向2輪型ロボットと比べて移動させるために難しい計算式を立てる必要があります。
メカナムホイールの逆?運動学
自分で導出した逆?運動学について解説していきます。
これは僕が高専一年生のときに導出したものなんですが、この数式でメカナムを制御している人は見たことないです...
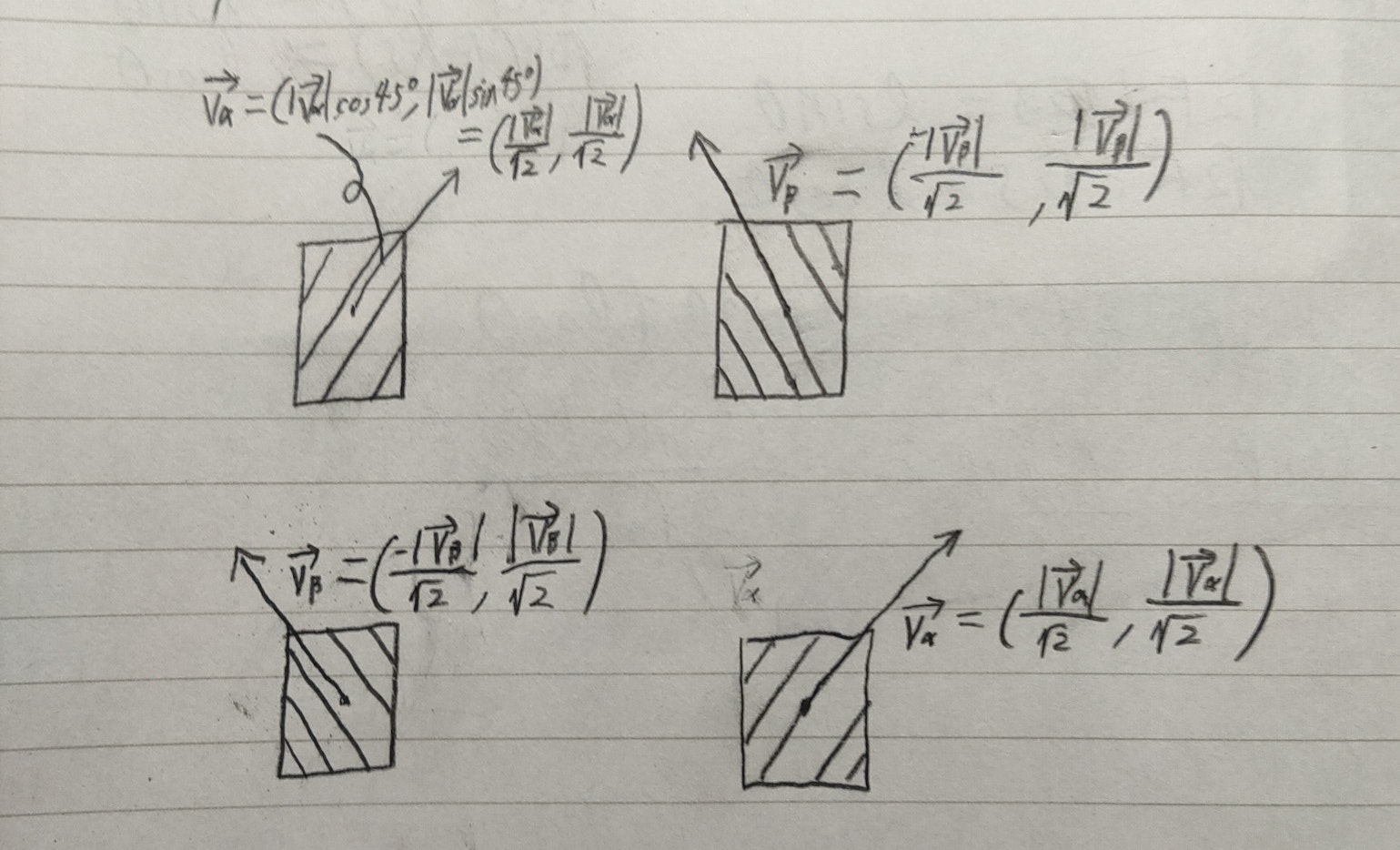
まず、上記のように各ホイールの速度ベクトル$\vec{v_\alpha}$,$\vec{v_\beta}$を考えます。ここで、各ホイールの対角線上にあるホイールは速度ベクトルの向きが互いに等しくなることから速度を同じにしても全方向移動が可能であることや、ここの速度が異なると旋回運動をしてしまうことから同じ速度にします。
すると、前述したようにメカナムホイールは車輪円周上に45度の角度でローラーが取り付けられていることから各速度ベクトルとx軸とのなす角は45度となるので、画像に示すように速度ベクトルを成分分解することができます。

また速度ベクトルを$\vec{v}$とすると、次のように成分表示することができます。
\vec{v}=(|\vec{v}|\cos{\theta},|\vec{v}|\sin{\theta})
従って、次のようにして任意の速度ベクトルのときの各ホイールの速度を求めることができます。
\begin{eqnarray}
\vec{v} &=& 2\vec{v_\alpha}+2\vec{v_\beta}\\
(|\vec{v}|\cos{\theta},|\vec{v}|\sin{\theta})&=&2\Bigl(\frac{|\vec{v_\alpha}|}{\sqrt{2}},\frac{|\vec{v_\alpha}|}{\sqrt{2}}\Bigr)+2\Bigl(-\frac{|\vec{v_\beta}|}{\sqrt{2}},\frac{|\vec{v_\beta}|}{\sqrt{2}}\Bigr)\\
(|\vec{v}|\cos{\theta},|\vec{v}|\sin{\theta})&=&(\sqrt{2}|\vec{v_\alpha}|,\sqrt{2}|\vec{v_\alpha}|)+(-\sqrt{2}|\vec{v_\beta}|,\sqrt{2}|\vec{v_\beta}|)\\
(|\vec{v}|\cos{\theta},|\vec{v}|\sin{\theta})&=&(\sqrt{2}|\vec{v_\alpha}|-\sqrt{2}|\vec{v_\beta}|,\sqrt{2}|\vec{v_\alpha}|+\sqrt{2}|\vec{v_\beta}|)\\
\end{eqnarray}
\therefore
\begin{cases}
|\vec{v}|\cos{\theta}&=&\sqrt{2}|\vec{v_\alpha}|-\sqrt{2}|\vec{v_\beta}|\\
|\vec{v}|\sin{\theta}&=&\sqrt{2}|\vec{v_\alpha}|+\sqrt{2}|\vec{v_\beta}|
\end{cases}
あとはこの連立方程式を$|v_\alpha|$,$|v_\beta|$について解くだけです。
消去法で解くことも勿論できますがここでは式が綺麗になるようにクラメルの公式を使って解きたいと思います。
この連立方程式を行列で表すと次のようになります。
\begin{pmatrix}
\sqrt{2} & -\sqrt{2}\\
\sqrt{2} & \sqrt{2}
\end{pmatrix}
\begin{pmatrix}
|\vec{v_\alpha}|\\
|\vec{v_\beta}|
\end{pmatrix}
=
\begin{pmatrix}
|\vec{v}|\cos{\theta}\\
|\vec{v}|\sin{\theta}
\end{pmatrix}
ここで
\begin{eqnarray}
\begin{vmatrix}
\sqrt{2} & -\sqrt{2}\\
\sqrt{2} & \sqrt{2}
\end{vmatrix}
&=&4\\
\begin{vmatrix}
\sqrt{2} & |\vec{v}|\cos{\theta}\\
\sqrt{2} & |\vec{v}|\sin{\theta}
\end{vmatrix}
&=&\sqrt{2}|\vec{v}|\sin{\theta}-\sqrt{2}|\vec{v}|\cos{\theta}\\
\begin{vmatrix}
|\vec{v}|\cos{\theta} & -\sqrt{2}\\
|\vec{v}|\sin{\theta}&\sqrt{2}
\end{vmatrix}
&=&\sqrt{2}|\vec{v}|\sin{\theta}+\sqrt{2}|\vec{v}|\cos{\theta}\\
\end{eqnarray}
なので、クラメルの公式から
\begin{cases}
\begin{eqnarray}
|\vec{v_\alpha}|&=&\frac{|\vec{v}|\sin{\theta}-|\vec{v}|\cos{\theta}}{2\sqrt{2}}\\
|\vec{v_\beta}|&=&\frac{|\vec{v}|\sin{\theta}+|\vec{v}|\cos{\theta}}{2\sqrt{2}}\\
\end{eqnarray}
\end{cases}
となります。
比率は合っているので速度を気にしなければそのままで全方向移動させることはできますが、実際に制御するのはメカナムホイールではなくモーターなので$|\vec{v_\alpha}|$,$|\vec{v_\beta}|$からモーターの回転数$[rpm]$を求める必要があります。
まず周速度$|\vec{v_{\alpha ps}}|$,$|\vec{v_{\beta ps}}|$は$|\vec{v_\alpha}|$,$|\vec{v_\beta}|$と下の画像のような関係があります。
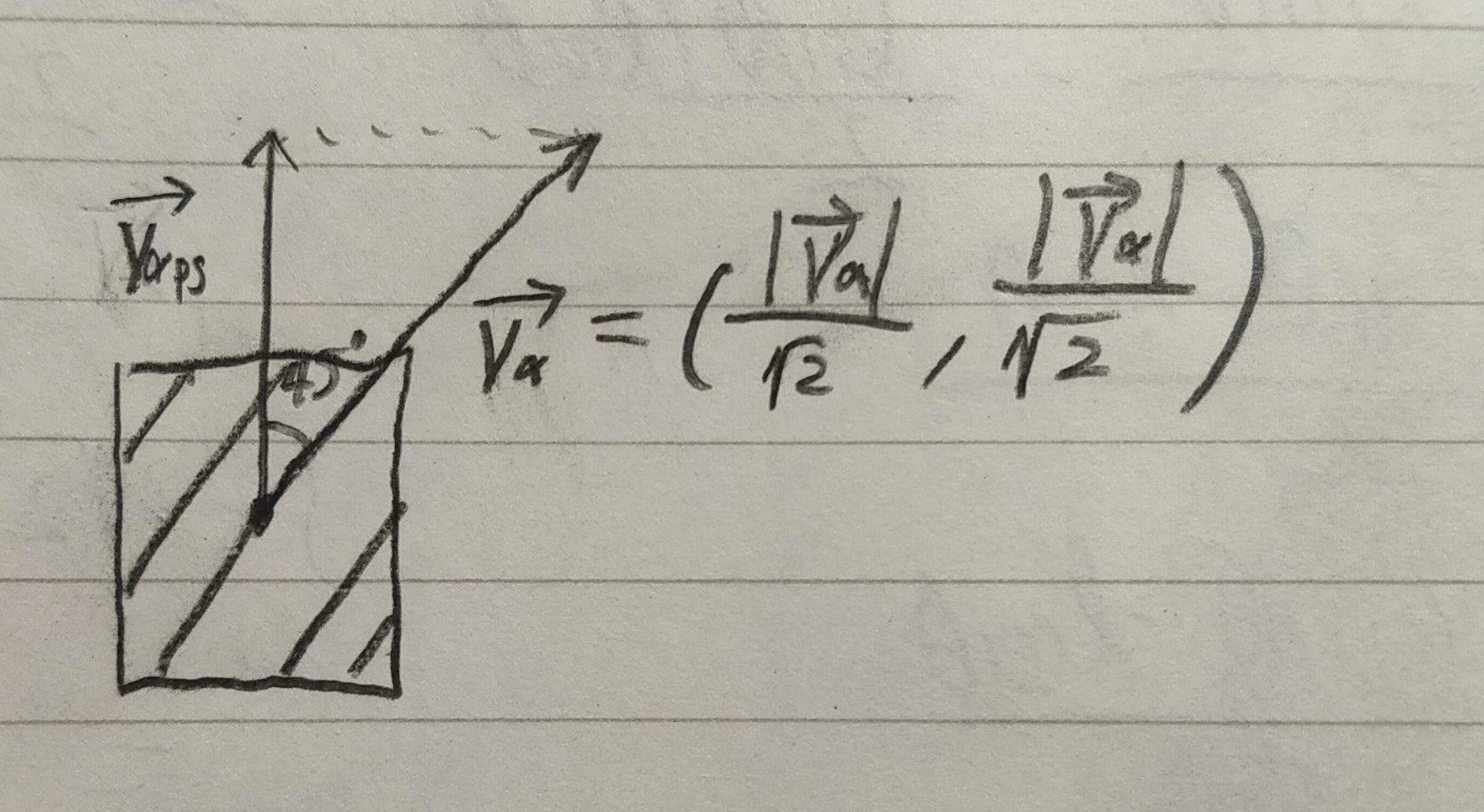
従って次式によって求めることができます。
\begin{eqnarray}
|\vec{v_{\alpha ps}}|&=&|\vec{v_\alpha}|\cos{\frac{\pi}{4}}=\frac{|\vec{v}|\sin{\theta}-|\vec{v}|\cos{\theta}}{4}\\
|\vec{v_{\beta ps}}|&=&|\vec{v_\beta}|\cos{\frac{\pi}{4}}=\frac{|\vec{v}|\sin{\theta}+|\vec{v}|\cos{\theta}}{4}
\end{eqnarray}
また、メカナムホイールの直径を$\Phi[m^2]$とすると周速度の定義から回転数$|\vec{v_{\alpha av}}|$,$|\vec{v_{\beta av}}|[rpm]$は
\begin{eqnarray}
|\vec{v_{\alpha av}}|&=&\frac{|\vec{v_{\alpha ps}}|}{\pi\Phi}=\frac{|\vec{v}|\sin{\theta}-|\vec{v}|\cos{\theta}}{4\pi\Phi}\\
|\vec{v_{\beta av}}|&=&\frac{|\vec{v_{\beta ps}}|}{\pi\Phi}=\frac{|\vec{v}|\sin{\theta}+|\vec{v}|\cos{\theta}}{4\pi\Phi}
\end{eqnarray}
と求めることができます。これで、ロボットの速度と移動方向から各モーターの回転数を求めることができました。
<追記(2022/02/19)>
旋回成分を無視して考えていたためこの数式だと旋回することができません。ホンマごめん、、、
反時計回りを正として、ロボットの角速度を$\omega$,ロボットの重心からメカナムホイールまでの距離を$L$とすると、回転の速度は$\omega L$となります。

このときの速度の方向は上の画像に示すように$L$と垂直な向き、即ち車軸に対して45[度]の位置にあります。従って旋回成分のみを考えたときの周速度$v_{ipsO}$は次のようになります。
\begin{eqnarray}
v_{1psO}&=&\omega L\cos{\frac{\pi}{4}\pi}=\frac{\omega L}{\sqrt{2}}\\
v_{2psO}&=&\omega L\cos{\frac{3}{4}\pi}=-\frac{\omega L}{\sqrt{2}}\\
v_{3psO}&=&\omega L\cos{\frac{3}{4}\pi}=-\frac{\omega L}{\sqrt{2}}\\
v_{4psO}&=&\omega L\cos{\frac{\pi}{4}}=\frac{\omega L}{\sqrt{2}}
\end{eqnarray}
よって、旋回成分のみを考えたときの回転数$v_{iavO}$は次のようになります。
\begin{eqnarray}
v_{1avO}&=&\frac{v_{1psO}}{\pi\Phi}=\frac{\omega L}{\sqrt{2}\pi\Phi}\\
v_{2avO}&=&-\frac{v_{2psO}}{\pi\Phi}=-\frac{\omega L}{\sqrt{2}\pi\Phi}\\
v_{3avO}&=&-\frac{v_{3psO}}{\pi\Phi}=-\frac{\omega L}{\sqrt{2}\pi\Phi}\\
v_{4avO}&=&\frac{v_{4psO}}{\pi\Phi}=\frac{\omega L}{\sqrt{2}\pi\Phi}
\end{eqnarray}
従って、旋回成分も含めた各モーターの回転数$v_{iavtrue}$は次のようになります。
\begin{eqnarray}
v_{1avtrue}&=&\frac{|\vec{v}|\sin{\theta}+|\vec{v}|\cos{\theta}+2\sqrt{2}\omega L}{4\pi\Phi}\\
v_{2avtrue}&=&\frac{|\vec{v}|\sin{\theta}-|\vec{v}|\cos{\theta}-2\sqrt{2}\omega L}{4\pi\Phi}\\
v_{3avtrue}&=&\frac{|\vec{v}|\sin{\theta}+|\vec{v}|\cos{\theta}-2\sqrt{2}\omega L}{4\pi\Phi}\\
v_{4avtrue}&=&\frac{|\vec{v}|\sin{\theta}-|\vec{v}|\cos{\theta}+2\sqrt{2}\omega L}{4\pi\Phi}
\end{eqnarray}
補足:mbedで制御する場合
この数式だけでは実際どのようにプログラムを組めばいいのかわからないので、mbedで(ブラシレスDCモータを用いて)メカナムホイールロボットを制御する場合について解説します。
まず、ブラシレスDCモータの回転数を制御するためにはブラシレスDCモータドライバにPWM信号を送る必要があります。PWM制御についてはここを見てもらえれば理解できると思いますが、ざっくり説明するとモータドライバにデューティー比1のPWM信号を送ると(チャージポンプ方式のモタドラとしてFET等での損失を無視すると)電源にモータを直接つないだのと同じ回転数で回り、デューティー比0.50のPWM信号を送ると電源に直接つないだ時の回転数×0.50の回転数で回ります。つまり、任意のデューティー比nのPWM信号を送ると電源に直接つないだ時の回転数×nの回転数で回ります。従って、モータの回転数を制御することはPWM信号のデューティー比を変えることで実現することが可能だとわかります。
このことから、デューティー比の範囲は0~1なので上の式の$v_{iavtrue}$を0~1に対応させる必要であるとわかると思います。デューティー比1の時電源にモータを直接つないだのと同じ回転数で回ることから、電源にモータを直接つないだ時の回転数を$v_{vcc}[rpm]$とすると、各モータに対応するモータドライバのピンへ入力するPWM信号のデューティー比$v_{iavtrueduty}$は次のようにして求まります。
\begin{eqnarray}
v_{1avtrueduty}&=&\frac{\frac{|\vec{v}|\sin{\theta}+|\vec{v}|\cos{\theta}+2\sqrt{2}\omega L}{4\pi\Phi}}{v_{vcc}}=\frac{|\vec{v}|\sin{\theta}+|\vec{v}|\cos{\theta}+2\sqrt{2}\omega L}{4v_{vcc}\pi\Phi}\\
v_{2avtrueduty}&=&\frac{\frac{|\vec{v}|\sin{\theta}-|\vec{v}|\cos{\theta}-2\sqrt{2}\omega L}{4\pi\Phi}}{v_{vcc}}=\frac{|\vec{v}|\sin{\theta}-|\vec{v}|\cos{\theta}-2\sqrt{2}\omega L}{4v_{vcc}\pi\Phi}\\
v_{3avtrueduty}&=&\frac{\frac{|\vec{v}|\sin{\theta}+|\vec{v}|\cos{\theta}-2\sqrt{2}\omega L}{4\pi\Phi}}{v_{vcc}}=\frac{|\vec{v}|\sin{\theta}+|\vec{v}|\cos{\theta}-2\sqrt{2}\omega L}{4v_{vcc}\pi\Phi}\\
v_{4avtrueduty}&=&\frac{\frac{|\vec{v}|\sin{\theta}-|\vec{v}|\cos{\theta}+2\sqrt{2}\omega L}{4\pi\Phi}}{v_{vcc}}=\frac{|\vec{v}|\sin{\theta}-|\vec{v}|\cos{\theta}+2\sqrt{2}\omega L}{4v_{vcc}\pi\Phi}
\end{eqnarray}
ここで、$v_{iavtrue}$がそれぞれ$v_{vcc}$より大きいと、デューティー比が1を超えてしまうので超えないように$|\vec{v}|$と$\omega$の範囲を決める必要があります。この計算式によって出てきた値をそれぞれPwmOutに入れてやることで制御することができます。最後に、具体的なプログラムを置いておきたいと思います。(全部載せるとどこがこの説明に該当するところかわかりにくいので部分的にします。)
//ここから通常移動
const double L=0.5;//ロボットの重心からメカナムホイールまでの距離[m](単位に注意...)
const double Phi=0.1;//メカナムホイールの直径[m]
const double v_vcc=180;//電源と直接つないだ時のモータの回転数[rpm]
const double v_length=0.5;//最大の速度:v_length[m/s]で動く
const double deg_length=10;//最大の角速度[deg/s]:deg_length[deg/s]で動く
const double rad_length=(deg_length*3.141592)/180;//rad_length[rad/s]で動く(数式に代入するのはradなの注意してください...)
double speed=sqrt(HORZ_left*HORZ_left+VERT_left*VERT_left)*v_length;
double rad=atan2(VERT_left,HORZ_left);/*ラジアン表記の角度を求める*/
double v_1=-(abs(speed)*sin(rad)+abs(speed)*cos(rad)+2.0*sqrt(2.0)*HORZ_right*rad_length*L)/(4.0*v_vcc*(3.141592)*Phi);
double v_2=(abs(speed)*sin(rad)-abs(speed)*cos(rad)-2.0*sqrt(2.0)*HORZ_right*rad_length*L)/(4.0*v_vcc*(3.141592)*Phi);
double v_3=(abs(speed)*sin(rad)+abs(speed)*cos(rad)-2.0*sqrt(2.0)*HORZ_right*rad_length*L)/(4.0*v_vcc*(3.141592)*Phi);
double v_4=-(abs(speed)*sin(rad)-abs(speed)*cos(rad)+2.0*sqrt(2.0)*HORZ_right*rad_length*L)/(4.0*v_vcc*(3.141592)*Phi);//v_1とv_4がマイナスなのは、この計算を導出する際の条件であるy軸方向正向きの回転を正としたとき、逆回転で正となるからです。
if(speed<=0.10&&abs(HORZ_right)<=0.10){
free_moter();
}else{//ここからクソコード
if(v_1>=0){
right_up_pwm.write(v_1);
right_up_dir=0;
}else{
right_up_pwm.write(-v_1);
right_up_dir=1;
}
if(v_2>=0){
left_up_pwm.write(v_2);
left_up_dir=0;
}else{
left_up_pwm.write(-v_2);
left_up_dir=1;
}
if(v_3>=0){
left_down_pwm.write(v_3);
left_down_dir=0;
}else{
left_down_pwm.write(-v_3);
left_down_dir=1;
}
if(v_4>=0){
right_down_pwm.write(v_4);
right_down_dir=0;
}else{
right_down_pwm.write(-v_4);
right_down_dir=1;
}
}
一応free_moter()の関数の中身はこれです。
void free_moter(){
left_down_pwm.write(0);
left_up_pwm.write(0);
right_down_pwm.write(0);
right_up_pwm.write(0);
left_down_dir=0;
left_up_dir=0;
right_down_dir=0;
right_up_dir=0;
}
終わりに
不明点や間違っているところがあれば連絡をお願いします。