ベイズ推論をJulia(&Turing.jl)でやってみた

概要

ベイズ推論入門として, 須山ベイズ¹のうち, 下記をJulia(Turing.jl)で実装してみた.

• Chapter3　ベイズ推論による学習と予測
  • 3.2 離散確率分布の学習と予測
    • 3.2.1 ベルヌーイ分布の学習と予測
  • 3.3 1次元ガウス分布の学習と予測
    • 3.3.1 平均が未知の場合
    • 3.3.2 精度が未知の場合
    • 3.3.3 平均・精度が未知の場合

なお、実装は学習までで, 予測はやってない.
(いや予測の実装がめんどかったんですよ）

実装は本に記載の解析解と, Turing.jlを用いた実装の両方行ってみた.

使用したもの

• Julia v1.9.2
• Distributions v0.25.99
• StatsPlots v0.15.6
• SpecialFunctions v2.3.0
• Turing v0.28.1

ベルヌーイ分布の学習

観測値$X=\{ x_1, x_2 , \dots, x_n \}$が$i.i.d$でベルヌーイ分布に従う場合, 即ち$x∼Bern(x|μ)=μx(1−μ)x$だとする($μ∈(0,1)$). この$μ$を学習により推定したい.
これは, 例えば$n$回コインを投げた結果, 表を1, 裏を0としたときに, そのコインの表の出る確率を推定することに相当する.
ベイズ推論による学習においては, この確率分布の, パラメータ(今回の場合はμ)が事前分布と呼ばれる確率分布に従う として, 観測データが与えられた下での, パラメータの事後分布を観測値から推定 することを行う.

理論

今回の場合, $μ \in (0,1)$であるので,

\begin{align}
p(\mu) &= \mathrm{Beta}(\mu | a,b) \\
&= C_B(a, b) \mu^{a - 1} (1-\mu)^{b - 1} \\
&\Bigl( C_B = \frac{\Gamma(a+b)}{\Gamma(a) + \Gamma(b)} \Bigr) \\
&\bigl( \Gamma(x) はガンマ関数を指す \big)
\end{align}

とμの従う分布を, ベータ分布と仮定する. 計算するとわかるが, こう仮定すると, 事後分布もベータ分布になる. つまり, ベータ分布はベルヌーイ分布の 共役事前分布 になっている.
$a$,$b$は事前分布のパラメータで超パラメータ（ハイパーパラメータ）と呼ばれる.
ベイズの定理より, 観測データ$X$が得られた際の事後分布は以下のよう.

\begin{align}
p( \mu | X) &= \frac{p(X | \mu)p(\mu)}{p(X)} \\
&= \frac{ \bigl\{ \prod_{m = 1}^n p(x_m|\mu) \bigr\} p(\mu)}{p(X)} \\
&(x_1, x_2, \dots はi,i,d) \\
&\propto \Bigl\{ \prod_{m = 1}^n p(x_m|\mu) \Bigr\} p(\mu) \\
&(\mu にかかわる項だけに注目するため, p(X)を省略)
\end{align}

となるので, あとはこれを計算すればよい.
対数をとって整理すると

\begin{align}
\ln p(\mu|X) &= \sum_{m=1}^n \ln{p(x_m|\mu) } + \ln{p(\mu)} +\rm{const} \\
&= \ln{\mu}\sum_{m=1}^n x_m + (1-\mu) \sum_{m=1}^{n}(1-x_m) + (a-1)\ln{\mu} + (b-1) + \ln{(1-\mu)} + \mathrm{const} \\
& = \ln{\mu}\Bigl\{ \sum_{m=1}^n x_m + a - 1 \Bigr\} + \ln{(1-\mu)}\Bigl\{ \sum_{m=1}^{n}(1-x_m) + b - 1 \Bigr\} + \mathrm{const} \\
& = \ln{\mu} \Bigl\{ \sum_{m=1}^n x_m + a - 1 \Bigr\} + \ln{(1-\mu)}\Bigl\{n - \sum_{m=1}^{n}x_m + b - 1 \Bigr\} + \mathrm{const} \\
& = (\hat{a}-1)\ln{\mu} + (\hat{b} - 1)\ln{(1-\mu)} + \mathrm{const} \\
&= \ln{\rm{Beta}(\mu|\hat{a}, \hat{b})} \\
&\Bigl( \hat{a} = \sum_{m=1}^n x_m + a, \hat{b} = n - \sum_{m=1}^{n}x_m + b \Bigr) \\ 
&\therefore p(\mu|X) = \mathrm{Beta}(\hat{a}, \hat{b})
\end{align} 

つまり, 事後分布がベータ分布になることがわかる.
また, $\hat{a}$について観察すると, $n$が小さいうちは超パラメータ$a$が支配的だが, $n$が大きくなると$x_m$の総和, 即ち何回観測データで1が出たかが支配的になる. $\hat{b}$についても同様に, $n$が小さいうちはbが支配的だが, $n$が大きくなれば$n−\sum_{m=1}^n x_m$が, 即ち観測データのうち何回0が出たかが支配的になる.

実装(解析解)

using Distributions
using SpecialFunctions
using StatsPlots

#観測データ生成
function MakeObservedDataForBernoulli(n, μ)
    d = Bernoulli(μ)
    return rand(d, n)
end

#事後分布生成
function MakeBernoulliPosterior(X, a, b)
    n = length(X)
    s = sum(X)
    hat_a = s + a
    hat_b = n - s + b
    return Beta(hat_a, hat_b) 
end

#観測データ生成～事後分布生成～事後分布プロット
function EstimatePosterior(n, μ, a, b)
    X = MakeObservedDataForBernoulli(n, μ)
    d = MakeBernoulliPosterior(X, a, b)
    plot(d,x_ticks = 0:0.05:1.0)
end

#実行
EstimatePosterior(200, 0.4, 5, 15) 

実行結果

↓EstimatePosterior(200, 0.4, 5, 15) の実行結果↓

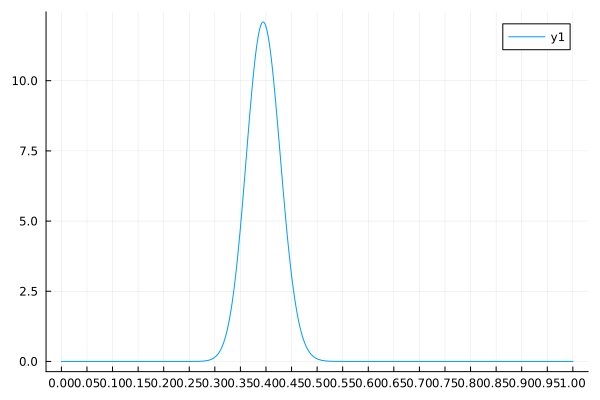
考察

実行結果を見てみると, 結構いい感じに推定できていそう.
ただ, 触ってみた感じとしては, 超パラメータを変な値にすると, 事後分布は超パラメータに引きずられた形になるようだ.
$\mu$が下式のようにベータ分布に従うとする.

\mu \sim \mathrm{Beta}(a, b)

この時, $\mu$の平均は

\mathbb{E}[\mu] = \frac{a}{a + b}

なので, $a/(a+b)$が真の値$\mu$からあんまりにも外れると、データ数が少ない場合は設定した超パラメータの影響を強く受けた事後分布になってしまうのだろう.

↓EstimatePosterior(200, 0.4, 1, 200) の実行結果↓

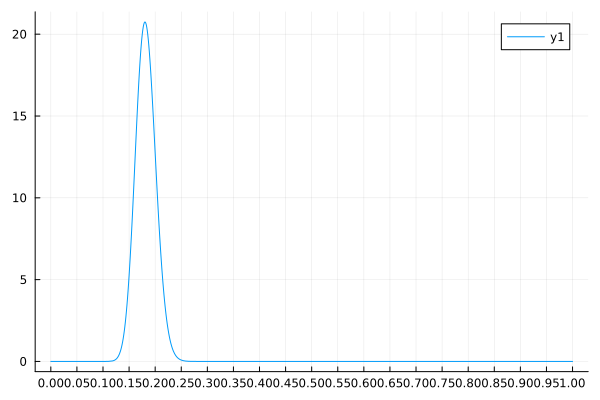
真の値$\mu = 0.4$に対して, $a/(a+b) \simeq 0.005$で推定しにかかるとこれくらいの結果になる.

ちなみに, データ数を増やしてみる(200→20,000)と以下くらいの結果になる.
↓EstimatePosterior(20000, 0.4, 1, 200) の実行結果↓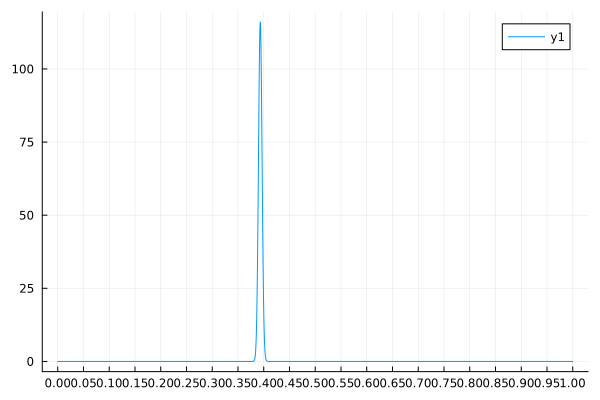

実行結果を見てみると, データ数が少ない時より 真の値付近に鋭くピークを持つ 事後分布になっていることがわかる.
ピークが鋭いというということは, このピークの値以外になっている確率が低いという推定結果になっている. つまり, よほどこの推定結果に自信があるんだろう. ベイズ推定ではこのように事後分布の形を眺めることでどれだけ自信がある結果なのかが教えてくれるのがいい.
まとめると

• データ数が少ないときは, 超パラメータに引きずられた事後分布になる.
• データ数が多いと超パラメータの影響が薄くなっていい感じ.

実装(Turing.jl)

using Turing
using Distributions
using StatsPlots

#観測データ生成
function MakeObservedDataForBernoulli(n, μ)
    d = Bernoulli(μ)
    return rand(d, n)
end

#modelの生成
@model function BernoulliModel(X, a, b)
    μ ~ Beta(a, b)
    n = length(X)
    for i in 1:n #for x in Xだとうまくいかない(？)
        X[i] ~ Bernoulli(μ)
    end
end

#事後分布の生成
function MakePosteriorBeroulliTuring(X, a, b, N = 4000)
    m = BernoulliModel(X, a, b)
    return sample(m, NUTS(), N) #MCMCを回してくれる
end

#観測データの生成～事後分布生成～事後分布可視化
function EsitmatePosteriorBernoulliTuring(n, μ, a, b)
    X = MakeObservedDataForBernoulli(n, μ)
    c = MakePosteriorBeroulliTuring(X, a, b)
    Plots.histogram(c)
end

EsitmatePosteriorBernoulliTuring(200, 0.4, 5, 15)

実行結果

↓EsitmatePosteriorBernoulliTuring(200, 0.4, 5, 15)の実行結果↓

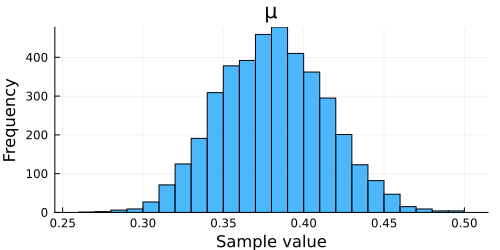
Turing.jlで実装した感想

なんかぱっと見はいい感じ.
まぁでも若干最初に設定した超パラメータに引きずられているっぽい感じはある.
(まぁ, ヒストグラムのプロットなんで, binの取り方とかで印象変わるのはありますけど)
書き心地としてはとっても楽. なんといっても解析解を求めなくても@modelをつけて, その中にモデルを書くだけで, 後は推論してくれるのが便利.
コメントでも書いたけど, 観測データの従う分布を実装するときにfor x in Xだとなぜかうまく動かない.for i in 1:nと書くかfor i in eachindex(X)と書く必要がある.
MCMCという手法を使って事後分布のシミュレーションを行うため, MCMCにどの方法を使うか(ハミルトンモンテカルロ使うとか, NUTS使うとか)指定したり, そのstep数を指定したりする必要があるので, 使いこなしたい場合はMCMCの知識も必要か.
しかし, MCMCの知識が全くない筆者でもこうやって, ベイズ推定が簡単にできるのはありがたい(本当にできてると言えるのかは別として).

1次元ガウス分布の学習

次は, 観測値$X = \{ x_1, x_2, \dots, x_n \}$が$i.i.d$で平均$\mu$, 分散$\sigma^2$のガウス分布に従うとした場合に, ベイズ推定を行ってみる.
ガウス分布は平均と分散の2パラメータで表現されるため, 何が既知で何が未知のパラメータなのかで以下の3パターンがある.

• 平均が未知（分散が既知）
• 分散が未知（平均が既知）
• 平均と分散が未知

分散について, 今後の計算を楽にするために精度パラメータ$\lambda = 1/\sigma^2$を導入しておく.

平均が未知の場合

平均$\mu$が未知の場合を扱っていく.
観測データの従う分布が

\begin{align}
p(x | \mu) &= N(x | \mu, \lambda^{-1}) \\
&= \sqrt{\frac{\lambda}{2\pi}} e^{-\frac{(x - \mu)^2\lambda}{2}}
\end{align}

であるとする.

理論

$\mu$の事前分布として, ガウス分布を採用する. 即ち,

p(\mu) = N(\mu | m, \lambda_{\mu}^{-1})

とする($m$, $\lambda_{\mu}^{-1}$はハイパーパラメータ).
ベイズの定理より,

\begin{align}
p(\mu|X) &\propto p(X|\mu) p(\mu) \\ 
&= \prod_{i = 1}^{n} p(x_i | \mu) p (\mu) \\
&= \prod_{i = 1}^{n} N(x_i | \mu, \lambda^{-1}) N(\mu | m, \lambda_{\mu}^{-1})
\end{align}

ベルヌーイ分布の時と同様に, 対数を取る.

\begin{align}
\ln{p(\mu|X)} &= \sum_{i=1}^{N}\ln{p(x_i|\mu)} + \ln{p(\mu)} + \rm{const} \\
&= \sum_{i=1}^{n}\ln{N(x_i|\mu, \lambda^{-1})} + \ln{N(\mu|m, \lambda_{\mu}^{-1})} + \rm{const} \\
&= -\sum_{i=1}^{n}\frac{(x_i-\mu)^2 \lambda}{2} - \frac{(\mu-m)^2 \lambda_{\mu}}{2} + \rm{const} \\
&= -\frac{1}{2} \Bigl\{ (n\lambda + \lambda_{\mu})\mu^2 -2\Bigl(\sum_{i=1}^N x_i \lambda + m\lambda_{\mu} \Bigr) \mu \Bigr\} + \rm{const} \\
\end{align}

実は, ガウス分布の対数をとったものは以下となる.

\ln{N(x|a,b^{-1})} = -\frac{1}{2} \Bigl( b x^2 - 2abx \Bigr) + \rm{const}

これと見比べると

\begin{align}
    \hat{\lambda}_{\mu} &= n\lambda + \lambda_{\mu} \\
    \hat{m} &= \frac{\lambda\sum_{i=1}^n x_i + m\lambda_{\mu}}{\hat{\lambda}_{\mu}}
\end{align}

と置くことで,

p(\mu | X) = N(\mu | \hat{m}, (\hat{\lambda_{\mu}})^{-1}) 

となり, $\mu$の事後分布がガウス分布として得られる.
$\hat{\lambda}_{\mu}$について観察すると観測数$n$とともに大きくなるので, 観測数が大きくなるにつれて, 事後分布の分散が小さくなる. 解釈するなら, 観測数が大きくなるにつれて, 推定結果に自信を持つようになるということだろうか. $\hat{m}$について観察すると, $n$が十分大きくなると$n$が絡まない項を無視して,

\begin{align}
\hat{m} \simeq \frac{\lambda \sum_{i = 1}^n x_i}{n \lambda} = \frac{\sum_{i = 1}^n x_i}{n} 
\end{align}

とまぁ直感的な結果が得られる.
ここまで観察してて思ったが, これ$\lambda_\mu$をかなり小さく取れば, 即ち事前分布の分散が大きいと相対的に観測結果が事後分布に強く影響するのではないか. それは結構直感的で, 事前分布の分散を大きくするということは, 超パラメータについてあまり情報が無いと解釈できるので, 観察結果に頼る部分が大きくなるということなのだろう.

実装(解析解)

using Distributions
using StatsPlots

#観測データ生成
function MakeObservedDataForGauss(n, μ, λ)
    d = Normal(μ, λ^(-1/2)) #Normal(μ, σ)
    return rand(d, n)
end

#事後分布生成
function MakeGaussPosteriorWithVariance(X, λ, m, λ_μ)
    n = length(X)
    hat_λ_μ = n * λ + λ_μ
    hat_m = (λ * sum(X) + m * λ_μ) / hat_λ_μ
    return Normal(hat_m, hat_λ_μ^(-1/2))
end

#観測データ生成～事後分布生成～事後分布プロット
function EstimatePosteriorWithVariance(n, μ, λ, m, λ_μ)
    X = MakeObservedDataForGauss(n, μ, λ)
    d = MakeGaussPosteriorWithVariance(X, λ, m, λ_μ)
    plot(d)
end

EstimatePosteriorWithVariance(200, 0.5, 1.0, 0, 10)

実行結果

↓EstimatePosteriorWithVariance(200, 0.5, 1.0, 0, 10)の実行結果↓

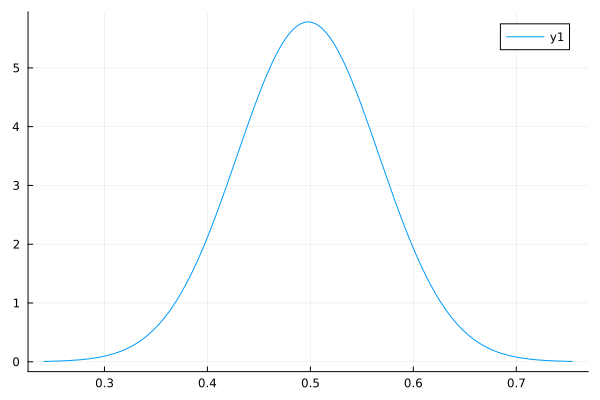
考察

うーん。結構いい感じ。
ただ、ベルヌーイ分布の時と同様に超パラメータを適当な値にするとやっぱり精度は落ちる.
↓EstimatePosteriorWithVariance(200, 0.5, 1.0, -10.0, 10)の実行結果

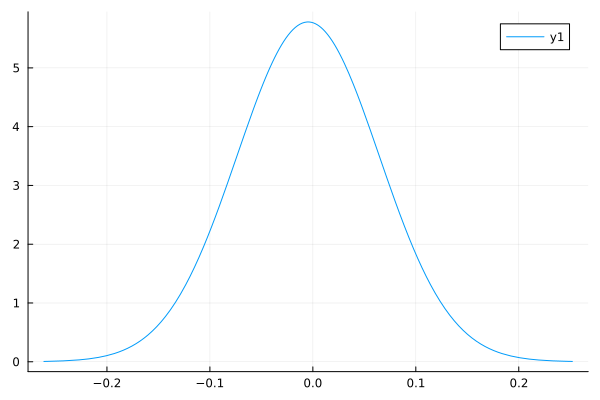
とはいえ超パラメータを適当な値にしても, 観測数が大きければ結構いい感じの値を出すのもベルヌーイ分布の時と変わらない.
↓EstimatePosteriorWithVariance(20000, 0.5, 1.0, -10.0, 10)の実行結果↓

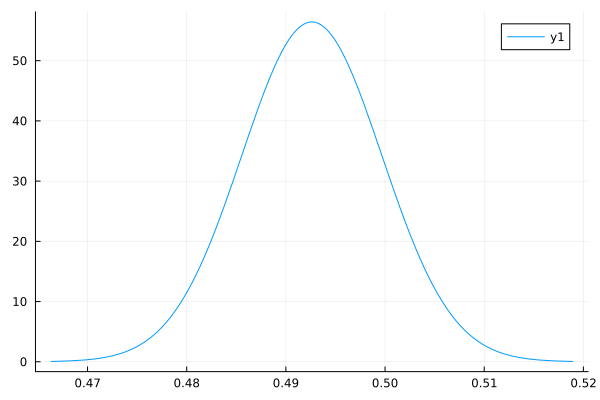
横軸を見るとわかるが, やっぱり事後分布の分散が小さくなっている. 観測数が100倍になったので, 分散もそれに応じて1/10程度になっている. 事後分布の分散$\hat{\lambda}_\mu$が$O(n)$なので, 妥当な結果であろう.

実装(Turing.jl)

using Turing
using Distributions
using StatsPlots

#観測データ生成
function MakeObservedDataForGauss(n, μ, λ)
    d = Normal(μ, λ^(-1/2)) #Normal(μ, σ)
    return rand(d, n)
end

#modelの生成
@model function GaussModelWithVariance(X, λ, m, λ_μ)
    n = length(X)
    μ ~ Normal(m, λ_μ^(-1/2))
    for i in 1:n
        X[i] ~ Normal(μ, λ^(-1/2))
    end
end

#事後分布の生成
function MakeGaussPosteriorWithVarianceTuring(X, λ, m, λ_μ, N = 4000)
    m = GaussModelWithVariance(X, λ, m, λ_μ)
    return sample(m, NUTS(), N)
end

#観測データの生成～事後分布生成～事後分布可視化
function EstimatePosteriorGaussWithVarianceTuring(n, μ, λ, m, λ_μ)
    X = MakeObservedDataForGauss(n, μ, λ)
    c = MakeGaussPosteriorWithVarianceTuring(X, λ, m, λ_μ)
    Plots.histogram(c)
end

EstimatePosteriorGaussWithVarianceTuring(200, 0.5, 1.0, 0, 10)

実行結果

↓EstimatePosteriorGaussWithVarianceTuring(200, 0.5, 1.0, 0, 10)の実行結果↓

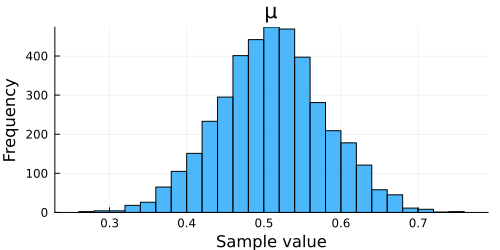
Turing.jlの実行結果について

結構いい感じ. 解析解と同じ感じの推定結果が得られている.

精度が未知の場合

今度は精度$\lambda$が未知の場合, 即ち分散が未知の場合をやってみよう.
観測データの従う分布が

\begin{align}
p(x | \lambda) &= N(x | \mu, \lambda^{-1}) \\
&= \sqrt{\frac{\lambda}{2\pi}} e^{-\frac{(x - \mu)^2\lambda}{2}}
\end{align}

であるとする.

理論

さて, 今回は精度パラメータ$\lambda$がモデリングの対象になるわけだが, $\lambda > 0$なので, $\lambda$の事前分布としては正の値のみをとる確率変数の従う分布を選択したい.
そこで, $\lambda$の事前分布としてガンマ分布を選択してみる.

\begin{align}
p(\lambda) &= \mathrm{Gam}(\lambda|a,b) \\
&=C_G(a,b) \lambda^{a-1} e^{-b\lambda} 
\end{align}

但し, $C_G(a, b)$は正規化定数を表す.
この仮定のもと, 実際に事後分布を計算してみる.

\begin{align}
    p(\lambda|X) &\propto p(X|\lambda)p(\lambda) \\
    &= \Bigl\{ \prod_{i=1}^n p(x_i|\lambda) \Bigr\} p(\lambda) \\
    &= \Bigl\{ \prod_{i=1}^n N(x_i|\mu, \lambda^{-1}) \Bigr\}\mathrm{Gam}(\lambda|a,b)
\end{align}

例によって, 対数をとる.

\begin{align}
\ln{p(\lambda|X)} &= \Bigl\{ \sum_{i=1}^n \ln{N(x_i|\mu, \lambda^{-1})} \Bigr\} + \ln{\mathrm{Gam}(\lambda|a,b)} + \mathrm{const} \\
&= -\frac{1}{2}\sum_{i=1}^n \Bigl\{ \ln{\lambda} - \lambda(x_i - \mu)^2 \Bigr\} + (a-1)\ln{\lambda} -b\lambda + \mathrm{const} \\
&=  \Bigl( \frac{n}{2} + a - 1 \Bigr)\ln{\lambda}  - \Bigl\{ \frac{1}{2} \sum_{i=1}^n (x_i - \mu)^2 + b \Bigr\} \lambda + \mathrm{const} \\
&=  (\hat{a} - 1)\ln{\lambda}  - \hat{b}\lambda + \mathrm{const} \\
\\
\Bigl( \hat{a} &= \frac{n}{2} + a,\ \hat{b} = \frac{1}{2}\sum_{i=1}^n (x_i - \mu)^2 + b \Bigr) \\
\end{align}

これと,

\ln \mathrm{Gam}(\lambda | a, b) = (a-1)\ln \lambda - b\lambda + \mathrm{const}

を見比べれば,

\begin{align}
    p(\lambda | X) &= \rm{Gam}(\hat{a}, \hat{b}) \\
    \Bigl( \hat{a} &= \frac{n}{2} + a,\ \hat{b} = \frac{1}{2}\sum_{i=1}^n (x_i - \mu)^2 + b \Bigr)
\end{align}

と, 事後分布を得ることができる.
事後分布の結果より明らかだが, ガンマ分布はガウス分布の精度に対する共役事前分布になっていたのである.
得られた結果を観察してみよう.

\mathbb{E} \Bigl[\mathrm{Gam}(\lambda | a, b) \Bigr] = \frac{a}{b}

であるので, 観測データの数$n$が大きくなった時には

\begin{align}
    \frac{\hat{a}}{\hat{b}} \simeq \frac{n}{\sum_{i=1}^n (x_i - \mu)^2} = \frac{1}{\mathrm{Var}[X]}
\end{align}

と, 直観と一致する結果が得られる.
また今までと同じように, 観測データが少ないうちは超パラメータである$a, b$の影響が強いのも一目瞭然である.

実装(解析解)

using Distributions
using StatsPlots

#観測データ生成
function MakeObservedDataForGauss(n, μ, λ)
    d = Normal(μ, λ^(-1/2)) #Normal(μ, σ)
    return rand(d, n)
end

#事後分布生成
function MakeGaussPosteriorWithMean(X, μ, a, b)
    n = length(X)
    hat_a = n / 2 + a
    hat_b = (sum(map(x -> (x - μ)^2 , X))/2 + b)
    return Gamma(hat_a, hat_b^(-1)) #Gamma(a, 1/b)
end

#観測データ生成～事後分布生成～事後分布プロット
function EstimatePosteriorWithMean(n, μ, λ, a, b)
    X = MakeObservedDataForGauss(n, μ, λ)
    d = MakeGaussPosteriorWithMean(X, μ, a, b)
    plot(d)
end

EstimatePosteriorWithMean(200, 0.5, 1.0, 0.8, 1.0)

実行結果

↓EstimatePosteriorWithMean(200, 0.5, 1.0, 0.8, 1.0)の実行結果↓

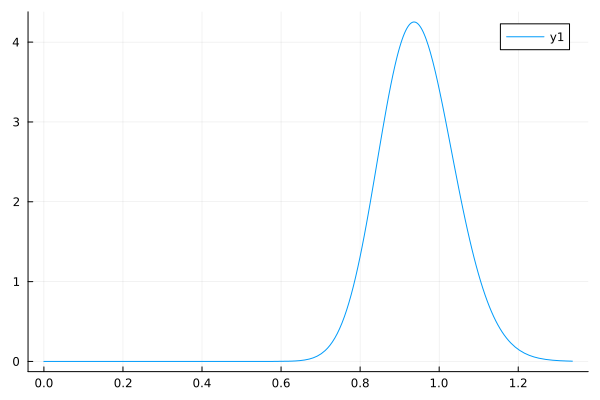
考察

やっぱり結構いい感じ。
当然, 超パラメータを極端な値にすると精度は落ちる.
↓EstimatePosteriorWithMean(200, 0.5, 1.0, 10.0, 1.0)の実行結果↓

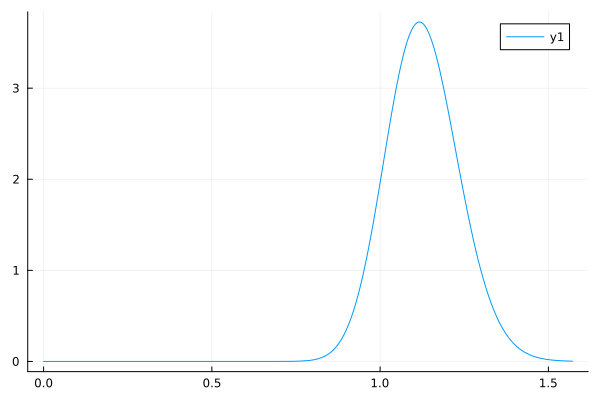
分散も大きくなっていて, 推定結果に自信がないのがわかる.

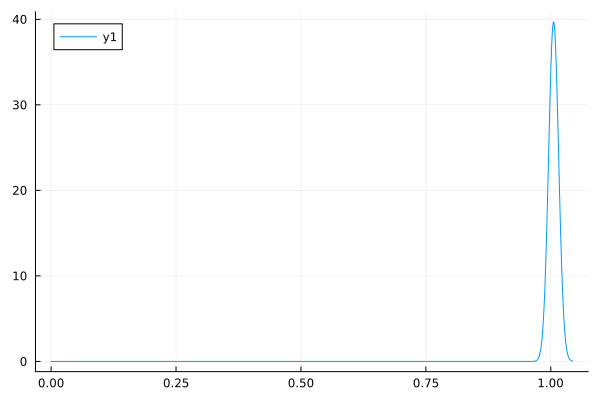
で, 観測数を大きくするといい感じになるのも今まで通り.
↓EstimatePosteriorWithMean(20000, 0.5, 1.0, 10.0, 1.0)の実行結果↓

実装(Turing.jl)

using Turing
using Distributions
using StatsPlots

#観測データ生成
function MakeObservedDataForGauss(n, μ, λ)
    d = Normal(μ, λ^(-1/2)) #Normal(μ, σ)
    return rand(d, n)
end

#modelの生成
@model function GaussModelWithMean(X, μ, a, b)
    n = length(X)
    λ ~ Gamma(a, b^(-1))
    for i in 1:n
        X[i] ~ Normal(μ, λ^(-1/2))
    end
end

#事後分布の生成
function MakeGaussPosteriorWithMeanTuring(X, μ, a, b, N = 4000)
    m = GaussModelWithMean(X, μ, a, b)
    return sample(m, NUTS(), N)
end

#観測データの生成～事後分布生成～事後分布可視化
function EstimatePosteriorGaussWithMeanTuring(n, μ, λ, a, b)
    X = MakeObservedDataForGauss(n, μ, λ)
    c = MakeGaussPosteriorWithMeanTuring(X, μ, a, b)
    Plots.histogram(c)
end

EstimatePosteriorGaussWithMeanTuring(200, 0.5, 1.0, 0.8, 1.0)

実行結果

↓EstimatePosteriorGaussWithMeanTuring(200, 0.5, 1.0, 0.8, 1.0)の実行結果↓

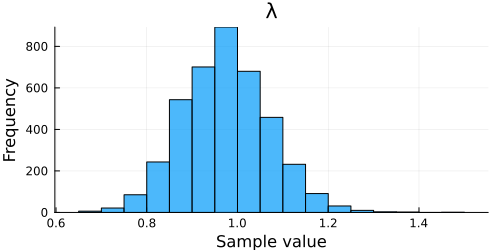
平均が未知の場合と同様いい感じ.
解析解とほぼ同様の結果が得られた.
実装するにあたって, ほとんど平均が未知の場合とコードが変わらないのが楽でいい.

平均・精度が未知の場合

最後に, 平均$\mu$と精度$\lambda$が両方とも未知の場合について推定を行う.
観測データの従う分布が

p(x| \mu, \lambda) = N(x | \mu, \lambda^{-1})

であるとする.

理論

$\mu$, $\lambda$についてバラバラに事前分布を設定して, ベイズの定理から事後分布を計算してもいいのだが, 同時に事前分布を, ガウス・ガンマ分布として設定すると, まったく同じ形の事後分布が得られる.
その様を見てみよう.
$\mu$, $\lambda$の事前分布として, 以下のガウス・ガンマ分布を設定する.

\begin{align}
    p(\mu, \lambda) &= \mathrm{NG}(\mu, \lambda | m, \beta, a, b) \\
    &= N(\mu | m , (\beta \lambda)^{-1}) \mathrm{Gam}(\lambda | a, b)
\end{align}

さて, ここからベイズの定理を用いて具体的な事後分布を計算するのもありだが, 今までの計算結果を用いて楽をしよう.
平均$\mu$については平均が未知の場合に求めた結果の$\lambda$を$\beta \lambda$に置き換えればよい.

\begin{align}
    p(\mu | \lambda, X) &= N(\mu |\hat{m}, (\hat{\beta}\lambda)^{-1}) \\
    \hat{\beta} &= N + \beta \\
    \hat{m} &= \frac{1}{\hat{\beta}}\Bigl( \sum_{i = 1}^n x_i + \beta \Bigr)
\end{align}

次に精度についてだが, まず同時分布を書き下す.

\begin{align}
    p(X, \mu, \lambda) &= p(\mu | \lambda, X) p(\lambda | X)p(X)
\end{align}

つまり,

\begin{align}
    p(\lambda | X) &= \frac{p(X, \mu, \lambda)}{p(\mu | \lambda, X) p(X)} \\
    & \propto \frac{p(X, \mu, \lambda)}{p(\mu | \lambda, X)}
\end{align}

を得る. $p(\mu | \lambda, X)$についてはすでに計算済み. 残る$p(X, \mu, \lambda)$は

\begin{align}
    p(X, \mu, \lambda) &= p(X | \mu, \lambda) p(\mu, \lambda)
\end{align}

を使えば計算ができそうである.
実際, 対数をとってひたすら計算すると

\begin{align}
    \ln{p(\lambda | X)} &= \Bigl( \frac{n}{2} + a- 1 \Bigr)\ln{\lambda} - {\frac{\lambda}{2} \Bigl( \sum_{i = 1}^{n} x^{2}_i + \beta m^2 - \hat{\beta} \hat{m}^2 \Bigr) - b \lambda }
\end{align}

となり,

\begin{align}
    p(\lambda | X) &= \mathrm{Gam}(\lambda|\hat{a}, \hat{b}) \nonumber \\
    \hat{a} &= \frac{n}{2} + a \nonumber \\
    \hat{b} &= {\frac{1}{2} \Bigl(\sum_{i = 1}^{n} x^{2}_i + \beta m^2 - \hat{\beta} \hat{m}^2 \Bigr) + b}
\end{align}

を得る.
以上をまとめて, 事後分布は

\begin{align}
    p(\mu, \lambda | X) &= p(\mu | \lambda, X) p(\lambda | X) \\
    &= N(\mu | \hat{m}, (\hat{\beta} \lambda)^{-1}) \mathrm{Gam}(\lambda | \hat{a}, \hat{b}))
\end{align}

と確かにガウス・ガンマ分布になっている.

実装(解析解)

using Distributions
using StatsPlots
using SpecialFunctions

#観測データ生成
function MakeObservedDataForGauss(n, μ, λ)
    d = Normal(μ, λ^(-1/2)) #Normal(μ, σ)
    return rand(d, n)
end

#事後分布生成
function MakeGaussPosterior(X, m, β, a, b)
    n = length(X)
    hat_β = n + β
    hat_m = (sum(X) + β)/hat_β
    hat_a = n / 2 + a
    hat_b = (sum(map(x -> x^2, X)) + β * m^2 - hat_β * hat_m^2 ) / 2 + b
    d_μ = (μ, m, λ) -> √(λ/2π) * exp(-(μ - m)^2 * λ / 2) #d_μ:μの事後分布
    d_λ = (λ, a, b) -> b^a * λ^(a-1) * exp(-b*λ) / gamma(a) #d_λ:λの事後分布
    d = (μ, λ) -> d_μ(μ, hat_m, λ) * d_λ(λ, hat_a, hat_b)
    return d
end

#観測データ生成～事後分布生成～事後分布プロット
function EstimatePosterior(n, μ, λ, m, β, a, b)
    X = MakeObservedDataForGauss(n, μ, λ)
    d = MakeGaussPosterior(X, m, β, a, b)
    range_μ = range(-1.0, 3.0, length = 100)
    range_λ = range(0, 3.0, length = 100)
    
    surface(range_μ, range_λ, d, colorbar = false, xlabel = "μ", ylabel = "λ")
end

EstimatePosterior(200, 1.0, 2.0, 0.8, 1.0, 3.0, 1.0)

実行結果

↓EstimatePosterior(200, 1.0, 2.0, 0.8, 1.0, 3.0, 1.0)の実行結果↓

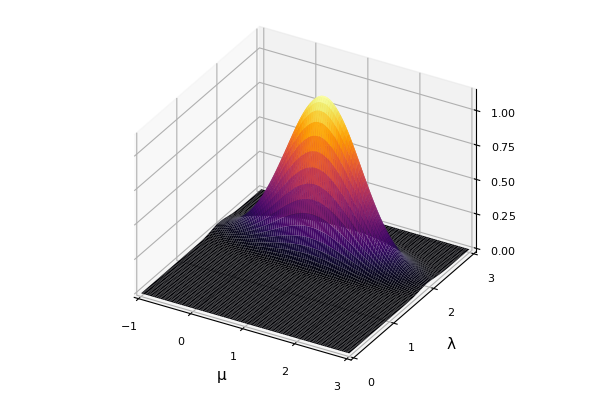
中々それっぽいのではないだろうか.
JuliaのPlot系はこうして簡単に3次元グラフもかけてしまうのがいい.
また事後分布の実装も, 関数を2つ用意して, それを合成した結果をreturnするだけでよいのだから手軽でよい.

実装(Turing.jl)

using Turing
using Distributions
using StatsPlots

#観測データ生成
function MakeObservedDataForGauss(n, μ, λ)
    d = Normal(μ, λ^(-1/2)) #Normal(μ, σ)
    return rand(d, n)
end

#modelの生成
@model function GaussModel(X, m, β, a, b)
    n = length(X)
    λ ~ Gamma(a, b^(-1))
    μ ~ Normal(m, β * λ)
    for i in 1:n
        X[i] ~ Normal(μ, λ^(-1/2))
    end
end

#事後分布の生成
function MakeGaussPosteriorTuring(X, m, β, a, b, N = 4000)
    m = GaussModel(X, m, β, a, b)
    return sample(m, NUTS(), N)
end

#観測データの生成～事後分布生成～事後分布可視化
function EstimatePosteriorGaussTuring(n, μ, λ, m, β, a, b)
    X = MakeObservedDataForGauss(n, μ, λ)
    c = MakeGaussPosteriorTuring(X, m, β, a, b)
    Plots.histogram(c)
end

EstimatePosteriorGaussTuring(200, 1.0, 2.0, 0.8, 1.0, 3.0, 1.0)

実行結果

↓EstimatePosteriorGaussTuring(200, 1.0, 2.0, 0.8, 1.0, 3.0, 1.0)の実行結果↓

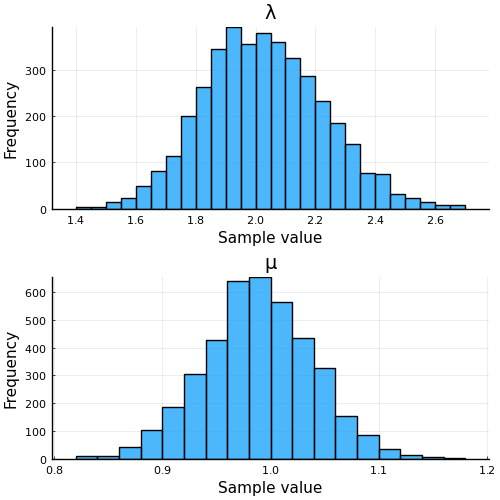
こちらもいい感じ。
Turing.jlのいいところはやっぱり, ちょろっとモデルを変えて実行がやりやすい.
今回のコードも, 平均が未知の場合のコードを少しいじっただけなので, 実装は一瞬で終えることができた.
モデルを色々といじりながら試してみたいことが多いベイズ推定において, この手軽さはなんとも心地良い.
ぜひ, 皆さんもJulia, Turing.jlを試してみてほしい.

1. 須山敦志. (2017). ベイズ推論による機械学習入門.杉山将監修.講談社. ↩