2回目の投稿なので、実質初投稿です。
概要
前回では、株価の対数価格を生成することを行いました。
本記事では生成した対数価格を用いて、価格の変動の激しさを表す"ボラティリティ"の推定を行います。今回も筆者に数学力が無いので"お気持ち"だけで進んでいきます。
目次
対象読者
前回とほぼ一緒です。
- 正規分布とかが(ふんわりでいいので)わかる人
- Juliaの基本的な文法(ifとかforとか)がわかる人
- (できれば)前回の記事を読んだ人
環境
これも前回と一緒です。
- Julia 1.5.3
- 使用パッケージ
- Distributions 0.24.4
- Plots 1.20.1
- Statistics
前回のあらすじ
前回は時刻$t$での株価$S_t$に対して、その対数価格$X_t \equiv \log{S_t}$の変動が以下のようになるというモデルの下で、対数株価のシミュレーションを行いました。
\begin{align}
dX_t = \mu dt + \sigma dW_t
\end{align}
実現ボラティリティについて
さて、今回は生成された対数価格$X_t$からボラティリティを推定することを行ってみましょう。
なぜボラティリティを推定したいの?
それは、ボラティリティはその資産の「リスク」を表すからです。
そもそもボラティリティとは、(ざっくり言えば)その資産の価格変動の度合いを示すものです。そして、金融の世界では、ボラティリティはその資産の「リスク」として考えられます。
なぜ資産の価格変動の度合いが「リスク」として考えられるのでしょうか?以下の例を考えてみましょう。
以下のような賭けを考えます。
- 賭け1:$\frac{1}{2}$の確率で+100円、$\frac{1}{2}$の確率で-100円
- 賭け2:$\frac{1}{2}$の確率で+10万円、$\frac{1}{2}$の確率で-10万円
さて、どちらの賭けも期待値は同じです。しかし、どちらの賭けのほうがより「安全」でしょうか?それは賭け1のほうだと考えるのが自然です。なぜならば賭け1では失ったとしても100円程度で済みますが、賭け2では失ったと場合10万円も失ってしまうからです。(まぁその分得られる金額もでかいんですけどね。)
このような詭弁例からもわかる通り、ボラティリティが大きいとその資産の「リスク」が大きいと言えそうです。
つまり、ボラティリティを推定することで、その資産がそれだけリスクを持っているかを推定することができると言えます。(ほんとぉ?)
累積ボラティリティと実現ボラティリティ
さて、ボラティリティを推定するわけですが、今回の推定のターゲットとなる**累積ボラティリティ(Integrated Volatility, IV)と、その推定量である実現ボラティリティ(Realized Volatility, RV)**について説明しておきましょう。
累積ボラティリティというのは一般に以下の量のことを指します。
\mathrm{IV} = \int_{0}^{T} \sigma^2 dt
これは、ボラティリティ$\sigma$の二乗を時間で積分したものなので、時間$[0,T]$におけるボラティリティの大きさを表すと解釈する思い込むことができそうです。
(???「それあなたの感想ですよね?」)
(余談)
なお、"今想定しているモデルでは"$\sigma$は定数なので、累積ボラティリティは以下の量でもあります。
\mathrm{IV} = \int_{0}^{T} \sigma^2 dt = \sigma^2 T
つまり、"今想定しているモデルでは"累積ボラティリティを推定できれば、$\sigma$が推定できるというわけですね。
(※わざわざ"今想定しているモデルでは"と強調しているのは理由があります。補足で述べますが、今回のモデルをちょっと拡張したモデルについては、常に累積ボラティリティから$\sigma$を推定できるわけではありません。)
さて、累積ボラティリティが推定できればボラティリティの大きさが推定できるわけですが、肝心の推定はどうすればいいでしょう?
実は、累積ボラティリティの一致推定量として下記の量、実現ボラティリティというのが知られています。
\mathrm{RV} = \sum_{i=1}^{n-1} (X_{t_{i+1}}-X_{t_i})^2
これは単に対数価格の差分を二乗して足しただけのものです。
"お気持ち"を説明すると、実現ボラティリティにおける$n$を$n \to \infty$とすれば、実現ボラティリティは累積ボラティリティに一致するので、$n$が大きければ実現ボラティリティによって精度良く累積ボラティリティを推定できるといった具合です。
(実は実現ボラティリティが累積ボラティリティの一致推定量となるためには色々と条件を満たすことが必要です。詳細は自分で調べてみてください。)
イメージ的には以下のような感じですね。
\mathrm{RV} \xrightarrow{n \to \infty} \mathrm{IV}
コード
では、実際にやってみましょう。
先にコードの全体をお見せします。
using Plots
using Random
using Distributions
using Statistics
function estimateVolatility(n,m)
#誤差(=RV-IV)を保存するための配列を宣言
result = Array{Float64}(undef,m)
for j in 1:m
#####ここからほぼ前回のコード#####
#---時間の生成---
T = 1
Δt = T/(n-1)
t = collect(0:Δt:T) #一定間隔Δtで、Tまで時間を生成
#---価格の生成---
#正規分布を生成
d = Normal(0,Δt^0.5) #dWは平均0,標準偏差Δt^0.5に従う
#正規分布に従う乱数を生成
ΔW = rand(d,n-1)
#対数価格変動をシミュレート
μ = 0.04
σ = 0.2
X = zeros(n)
X[1] = 10 #初期対数価格X_1を設定
for i in 1:n-1
X[i+1] = X[i] + μ*Δt + σ*ΔW[i]
end
#####ここまでほぼ前回のコード#####
#---実現ボラティリティ(RV),累積ボラティリティ(IV)を計算---
RV = 0
for i in 1:n-1
RV += (X[i+1]-X[i])^2
end
IV = σ^2*T #今回のケースではIVはこうなる
#---推定結果の記録---
result[j] = RV - IV
end
#---誤差の表示---
println("---result---")
println("Average:",mean(result))
println("Std:",std(result))
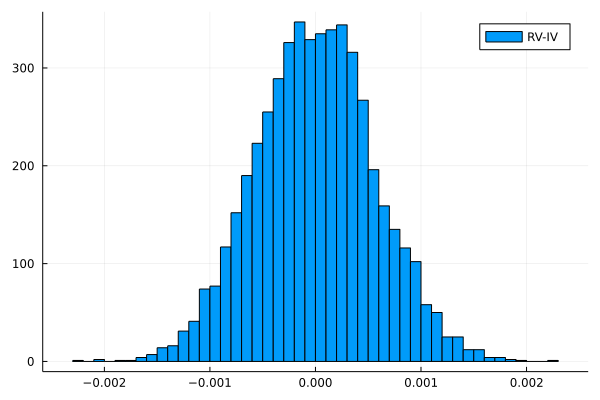
plot(result,st = :histogram,label = "RV-IV") #ヒストグラムを表示
end
estimateVolatility(10000,5000)
実行結果
上記のコードを実行すると、以下のような感じで誤差の平均、標準偏差、ヒストグラムが出力されるかと思います。
---result---
Average:-1.2419854575511508e-7
Std:0.0005650675372142399
ヒストグラムを見てみると正規分布っぽくなってますね。
上記のプログラムの$n$を大きくすると(つまり対数価格の観測数を大きくすると)、この誤差の分布の分散が段々小さくなっていきます。
(興味ある人はやってみてください。)
解説
解説というか釈明をしていきたいと思います。
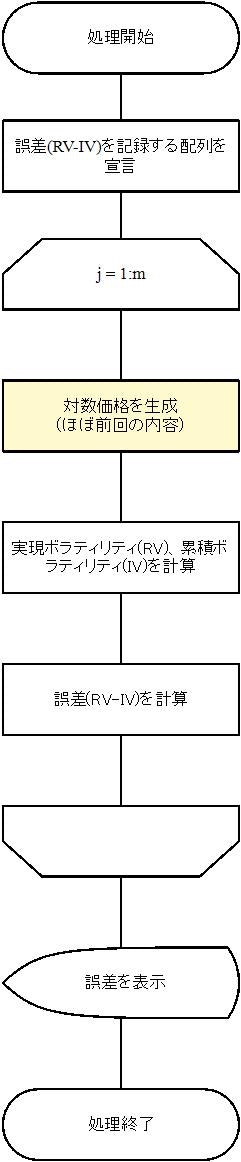
このコードの処理の概要は下記のようになっています。
誤差を記録する配列を宣言
推定結果として、誤差を記録する配列を宣言しておきます。
宣言した配列resultには以下のように値を入れていきます。
result[j] = j回目の誤差(=RV-IV)
対数価格の生成
ここはほぼ前回のコードのままです。
RV,IVの計算
実現ボラティリティ(RV)は
\mathrm{RV} = \sum_{i=1}^{n-1} (X_{t_{i+1}}-X_{t_i})^2
に基づいて計算するだけです。
累積ボラティリティ(IV)ですが、余談で述べたように今回の場合は
\mathrm{IV} = \int_{0}^T \sigma^2 dt = \sigma^2 T
となるので、これに基づいて計算するだけです。
誤差の計算
ここは別に解説いらないでしょ
推定誤差(=RV-IV)を計算して、resultに格納するだけです。
誤差を表示
ここで誤差の平均、標準偏差、ヒストグラムを出力しています。
パッケージStatisticsに備わっているavgという関数と、stdという関数で平均と標準偏差を出しています。(適当に配列突っ込んどけば計算してくれるんでJuliaはいいですね!)
続いて、前回も使用したPoltsの力を借りて、誤差のヒストグラムをプロットしています。ヒストグラムを表示するのは簡単で、
plot(データ, st = :histogram)
とすればいいです。
補足
今回、モデルとして前回用いたブラック・ショールズモデル
\begin{align}
dX_t = \mu dt + \sigma dW_t
\end{align}
を用いました。
余談で少し触れましたが、これを拡張したものとして下記のように、$\mu$と$\sigma$が時間によって変化するというものがあります。
\begin{align}
dX_t = \mu_t dt + \sigma_t dW_t
\end{align}
この時、累積ボラティリティは
\mathrm{IV} = \int_{0}^{T} \sigma_t^2 dt
となります。やはりこの場合でも(諸々の条件を満たすならば)、実現ボラティリティが累積ボラティリティの一致推定量になります。
但し、このように$\sigma_t$が時間によって変化する場合には余談でやったように、累積ボラティリティから$\sigma_t$を推定することはできません。
終わりに
今回は、対数価格から実現ボラティリティ(RV)を計算し、ボラティリティの大きさを表す累積ボラティリティ(IV)を推定することを行いました。
なんだか色々書こうとして内容がとっ散らかってしまった感がありますね...
読みにくい文章で申し訳ございません。
次回は、今回のテーマでもあった実現ボラティリティに関して、高頻度観測に伴うマーケットマイクロストラクチャーノイズ絡みの話でも書こうかと思っています。