#前回までのあらすじ
SHA256の暗号化を行うためには、どのようなデータを入力しても処理結果が全く異なるように入力データを成型する必要があります。この処理をパディング処理といいますが、前回はパディング処理の実装ができたところまで報告しました。
#SHA-256の暗号化処理（本体）
今回は本体である暗号化処理を実装しました。暗号化処理の概要は下記のようになっておりNISTでも仕様書として公開されています。
https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf
この仕様書をもとに実装を行いました。
##論理演算を行う関数を実装
暗号化を行うためにいくつかの論理演算をする関数を定義する必要があります。いくつかのC言語で実装されている暗号化プログラムやOpenSSLのソースを読むと、これらの関数はマクロで実装されており、プリプロセッサでインライン展開されるような実装がされていました。今回のソースコードでもC言語のマクロを使って関数を実装しました。
上記の論理演算関数の実装は下記のようになります。
// 4.1.2 SHA-224 and SHA-256 Functions
#define ROTR(x,n) ((x >> n | x << (32 -n)))
#define SHR(x,n) ((x >> n))
#define Ch(x,y,z) ((x & y) ^ (~x & z))
#define Maj(x,y,z) ((x & y) ^ (x & z) ^ (y & z))
#define SIGMA0(x) ((ROTR(x, 2) ^ ROTR(x, 13) ^ ROTR(x, 22)))
#define SIGMA1(x) ((ROTR(x, 6) ^ ROTR(x, 11) ^ ROTR(x, 25)))
#define sigma0(x) ((ROTR(x, 7) ^ ROTR(x, 18) ^ SHR(x, 3)))
#define sigma1(x) ((ROTR(x, 17) ^ ROTR(x, 19) ^ SHR(x, 10)))
##定数を定義
暗号化処理を行う初期値として定数の配列を定義します。これも論文で定義されているため、同じように定義します。
定数の定義は下記のように設定しました。
// 4.2.2 SHA-224 and SHA-256 Constants
const unsigned int K[64] = {
0x428a2f98UL, 0x71374491UL, 0xb5c0fbcfUL, 0xe9b5dba5UL, 0x3956c25bUL, 0x59f111f1UL, 0x923f82a4UL, 0xab1c5ed5UL,
0xd807aa98UL, 0x12835b01UL, 0x243185beUL, 0x550c7dc3UL, 0x72be5d74UL, 0x80deb1feUL, 0x9bdc06a7UL, 0xc19bf174UL,
0xe49b69c1UL, 0xefbe4786UL, 0x0fc19dc6UL, 0x240ca1ccUL, 0x2de92c6fUL, 0x4a7484aaUL, 0x5cb0a9dcUL, 0x76f988daUL,
0x983e5152UL, 0xa831c66dUL, 0xb00327c8UL, 0xbf597fc7UL, 0xc6e00bf3UL, 0xd5a79147UL, 0x06ca6351UL, 0x14292967UL,
0x27b70a85UL, 0x2e1b2138UL, 0x4d2c6dfcUL, 0x53380d13UL, 0x650a7354UL, 0x766a0abbUL, 0x81c2c92eUL, 0x92722c85UL,
0xa2bfe8a1UL, 0xa81a664bUL, 0xc24b8b70UL, 0xc76c51a3UL, 0xd192e819UL, 0xd6990624UL, 0xf40e3585UL, 0x106aa070UL,
0x19a4c116UL, 0x1e376c08UL, 0x2748774cUL, 0x34b0bcb5UL, 0x391c0cb3UL, 0x4ed8aa4aUL, 0x5b9cca4fUL, 0x682e6ff3UL,
0x748f82eeUL, 0x78a5636fUL, 0x84c87814UL, 0x8cc70208UL, 0x90befffaUL, 0xa4506cebUL, 0xbef9a3f7UL, 0xc67178f2UL
};
結果配列を格納するための初期値も下記のように定義します。
// 5.3.3 SHA-256
const unsigned int H0[] = {
0x6a09e667UL, 0xbb67ae85UL, 0x3c6ef372UL, 0xa54ff53aUL, 0x510e527fUL, 0x9b05688cUL, 0x1f83d9abUL, 0x5be0cd19UL
};
##暗号化処理本体を実装
暗号化を行う実際の処理本体を実装しました。今回の実装ではパディング処理されたブロックの配列（メッセージブロック）を受け取って、ハッシュ化された３２個の整数を返す関数を実装しました。
###1.W配列の初期値を計算
論文では下記の箇所から解説されています。
メッセージブロック分をループするため、まずメッセージブロックが何ブロックあるのかをカウントします。
その後ブロックごとに演算処理を行います。
/**
SHA256暗号化処理
処理内容：パディングされたメッセージブロックを受け取って暗号化処理を行い
暗号化処理結果を返却します。
引数：メッセージブロック（パティング処理の戻り値）
暗号化処理結果を格納する整数の配列（３２個分）
戻り値：なし
*/
void SHA256::compute(unsigned char** block, unsigned int* H) {
// メッセージの個数をカウントする
int N = 0;
while (block[N] != NULL) {
N++;
}
unsigned int W[MESSAGE_BLOCK_SIZE];
// Hを初期化する
memcpy(H, H0, sizeof(int) * INIT_HASH_LENGTH);
// 6.2.2 SHA-256 Hash Computation
for (int i = 0; i < N; i++) {
// 変数定義
unsigned int a, b, c, d, e, f, g, h, s0, s1, T1, T2;
// 1. Prepare the message schedule, { Wt }:
char* msg = (char*)block[i];
for (int t = 0; t < MESSAGE_BLOCK_SIZE; t++) {
if (t < 16) {
int p = t * 4;
W[t] = (unsigned int)((msg[p] & 0xff) << 24) | (unsigned int)((msg[p + 1] & 0xff) << 16) | (unsigned int)((msg[p + 2] & 0xff) << 8) | (unsigned int)(msg[p + 3] & 0xff);
}
else {
W[t] = sigma1(W[(t - 2)]) + W[(t - 7)] + sigma0(W[(t - 15)]) + W[(t - 16)];
}
}
１ブロックは64バイトのため、64個分の初期値を計算します。
最初の16個は64バイトのブロックを4バイトずつ連結して整数化して16個の整数を作り出します。
残りの17個目～64個目までは自分のバイト以前のW値を元に計算を行って計算します。
###2.演算変数の初期化処理
論文ではa～hまでの8個の変数を使って演算処理を行います。ここでは論文に従って８個を初期化します。
// 2. Initialize the eight working variables, a, b, c, d, e, f, g, and h, with the (i-1)st hash value:
a = H[0];
b = H[1];
c = H[2];
d = H[3];
e = H[4];
f = H[5];
g = H[6];
h = H[7];
###3.演算処理
SHA256の根幹となる演算処理ですが、先ほどのa～hの8個の変数を順番に入れ替えながら0~63までのW値を元に計算を行います。
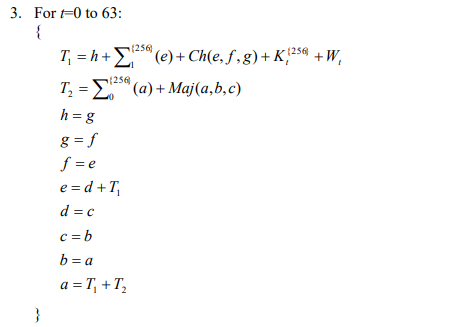
// 3. For t=0 to 63:
for (int t = 0; t < MESSAGE_BLOCK_SIZE; t++) {
T1 = h + SIGMA1(e) + Ch(e, f, g) + K[t] + W[t];
T2 = SIGMA0(a) + Maj(a, b, c);
h = g;
g = f;
f = e;
e = d + T1;
d = c;
c = b;
b = a;
a = T1 + T2;
}
###4.加算処理
最後に計算されたa～hの結果をH配列に加算します。
// 4. Compute the ith intermediate hash value H(i):
H[0] = (a + H[0]) & 0xffffffff;
H[1] = (b + H[1]) & 0xffffffff;
H[2] = (c + H[2]) & 0xffffffff;
H[3] = (d + H[3]) & 0xffffffff;
H[4] = (e + H[4]) & 0xffffffff;
H[5] = (f + H[5]) & 0xffffffff;
H[6] = (g + H[6]) & 0xffffffff;
H[7] = (h + H[7]) & 0xffffffff;
これらの１～４までの演算をメッセージブロック数分の演算を行い、最後に加算されたH配列が最終的な暗号結果となります。
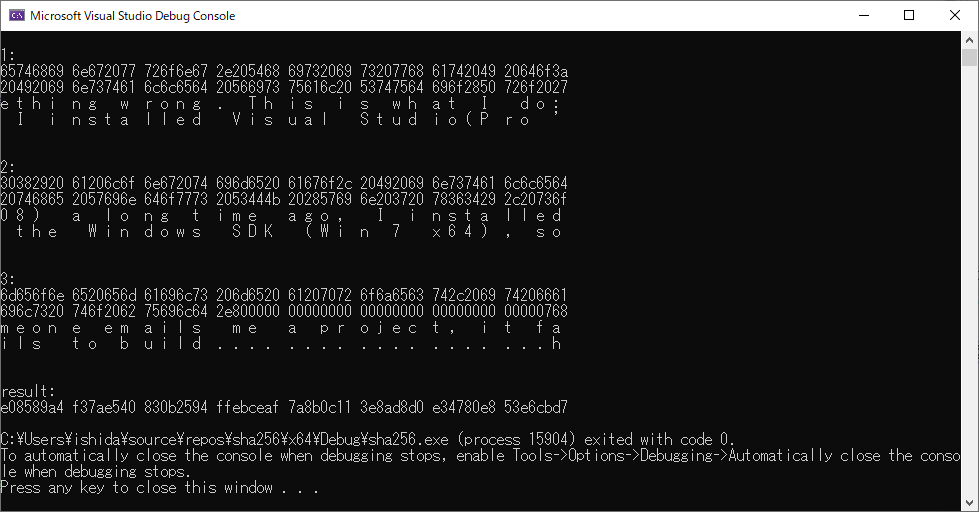
#動作検証
動作検証はopensslコマンドを使用して出力された演算結果とプログラムの値が同じかどうかを比較します。
openssl のコマンドは下記のように入力します。
$ echo -n "Visual Studio drives me crazy and I am suspecting I am doing something wrong. This is what I do: I installed Visual Studio(Pro '08) a long time ago, I installed the Windows SDK (Win 7 x64), someone emails me a project, it fails to build." | openssl dgst -sha256
(stdin)= e08589a4f37ae540830b2594ffebceaf7a8b0c113e8ad8d0e34780e853e6cbd7
実際にプログラムで出力された内容を表示します。
全く同じ「e08589a4 f37ae540 830b2594 ffebceaf 7a8b0c11 3e8ad8d0 e34780e8 53e6cbd7」という値が出力されました。
実装内容は下記のGitHubに公開しております。
https://github.com/ishida0219/sha256
#苦労したところ
暗号化処理を実装する上で一番苦労した点が出力結果の検証でした。
いろいろとネット上でソースを漁ったのですが、JavaScriptで書かれているものや、ソース通りに実装しても処理結果が異なったりして、最終的にNISTの論文から自分で実装するしかないと考えました。
ただ、処理結果を検証するにしても openssl の処理結果と全く違う値が出力され、計算の過程で何が違うのかがつかめませんでした。
行き詰っているところにGIGAZINEで紹介されていたSHA256暗号化の処理過程をアニメーションで表示するプログラムが存在するという記事を発見しました。
https://gigazine.net/news/20200514-sha-256-animation/
https://github.com/in3rsha/sha256-animation
この sha256-animation という ruby で書かれたプログラムはアニメーションの途中経過をエンターキーで進めるステップ実行の機能があり、その演算過程と自分の実装の内容があっているかを１ステップずつ検証していきました。
検証を進めていくと、マクロで定義していた関数に問題があることがわかり、本当は論理和をしなければならないところを加算していたことが判明しました。
// 誤
#define ROTR(x,n) (((x >> n) + (x << (32 -n))))
// 正
#define ROTR(x,n) ((x >> n | x << (32 -n)))
一見正しいような内容なのですが論理和と加算では結果が違っており、１ビットだけ違うような箇所がまれに出ていました。
最終的に１つずつ検証を重ね、openssl の検証結果とまったく一致したときはとても大きな喜びを得ることができました。