ポリゴン加工における刃の挙動

概要

ポリゴン加工

工作機械で行う旋削加工の一つに、ポリゴン加工という方法があります。
刃物とワーク（加工対象物）の回転比を2：1にして削るとワークを多角形に加工できるというもので、多角形の加工を非常に効率的に行える加工です。
イメージはこちらなどがわかりやすいです。
http://www.nittopolygon.com/01polygon.html
刃をn枚配置すると2n角形ができます。

やりたい事

この加工を知った時は回転だけで綺麗な多角形が削れることに感動したのですが、

• なぜ回転運動だけで直線が加工できるのか。そもそも本当に直線なのか。
• 回転比2:1という値に数学的な意味があるのか
• 奇数角形はできないのか

など疑問が湧いてきたので刃の挙動を描画してみることにしました。

刃の挙動を求める式

元になる情報

こちらの方がすでに同じ事をされているので基本的にこれを見ればいいのですが、自分の理解のため少し順を追って説明します。またMathmaticaを使っているようなので、Pythonで再実装してみます。
https://fyang2.stanford.edu/hardware/polygon-turning.html

式

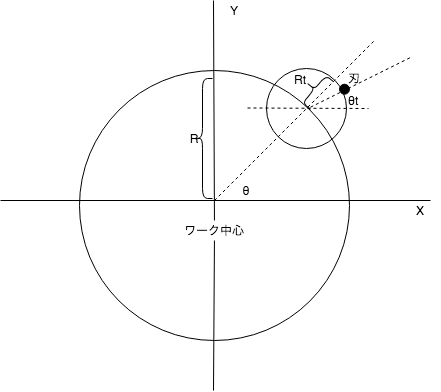
刃がワークに対してどう動くかを考えたいので、ワークの座標を固定し、その場合の工具の刃の挙動を考えます。

• ワークの回転中心と工具の回転中心の距離 : R
• 工具の半径 : Rt
• ワークの回転角度 : θ
• 工具の刃の回転角度 : θt
• 回転比 : k（k=2の時、刃物とワークの回転比が2：1）

とします。

その場合、工具の回転中心の座標は単純に
Xtc = R * cosθ
Ytc = R * sinθ
です。これは簡単。
次は刃の位置ですが、工具の回転中心からの座標は以下となります。
Xt = Rt * cosθt
Yt = Rt * sinθt
したがって刃の軌跡はXtc+Xt, Ytc+Ytとなり、以下で表せます。
X = R * cosθ + Rt * cosθt
Y = R * sinθ + Rt * sinθt

ここでθtをθで表す必要があります。結論から言うとθt = -(k-1)θとなりますが、これについて説明します。
まずマイナスが付くのは、ポリゴン加工時のワークと工具の回転方向が逆になるためです。
k-1についてですが、
回転比が同じ場合(k=1の場合)、ワークを中心に考えると工具側は自転していない様に見えます。なので常に0*θ=0となります。k=2の時に初めて1回転している様に見えます。(= -θ)。同様に3,4,5...と増えていくと、-2*θ、-3* θ、-4* θ...という風に増えていくことになります。
もう少しちゃんとした説明があると思いますが、ひとまずその様な理屈でθt=-(k-1)θとなります。

したがって、刃の軌跡は以下となります。
X = R * cosθ + Rt * cos(-(k-1)θ)
Y = R * sinθ + Rt * sin(-(k-1)θ)

刃先が複数の場合

工具には等間隔に刃先を複数枚つけられます。それも考慮に入れます。
刃先の数をnとするとi番目の刃先の位置は 2π*i/n分だけ位相がずれるので、
Xi = R * cosθ + Rt * cos(-(k-1)θ + 2π*i/n)
Yi = R * sinθ + Yt = Rt * sin(-(k-1)θ+ 2π*i/n)
となります。

実装

これらを元にpython(jupyter notebook)で実装してみます。
まず必要なモジュールのインポート

notebook

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

グラフを書く処理を一部関数化します。

notebook

def create_ax(xlim, ylim):
    """
    matplotlibのfig,axを作成して返す。figsizeは固定。
    """
    fig = plt.figure(figsize=(6,6))
    ax = fig.add_subplot(111)
    ax.grid()
    ax.set_title("Polygon orbit")
    ax.set_xlim(xlim[0],xlim[1])
    ax.set_ylim(ylim[0],ylim[1])
    return fig, ax

def draw_data(ax,x,y, color="blue"):
    """
    与えられたx,yをaxに描画。ついでに原点も描画。
    """
    ax.set_xlabel("x", fontsize=16)
    ax.set_ylabel("y", fontsize=16)
    ax.plot(x,y,color=color)
    ax.scatter(0,0,color="black")

主役の刃の軌跡を返す関数。前段で導出した式を使います。ついでに円の軌跡を返す関数も追加。

notebook

def circle_data(R, theta):
    """
    θが与えられた場合の、円のx,y座標を返す。
    """
    x = R * np.cos(theta)
    y = R * np.sin(theta)
    return x, y

def poly_data(R,Rt, k, theta, n=1,i=0):
    """
    θが与えられた場合の、刃の軌跡のx,y座標を返す。
    """
    d = 2 * np.pi * i / n # 位相の算出
    x = R* np.cos(theta) + Rt * np.cos(-(k-1)*theta +d)
    y = R* np.sin(theta) + Rt * np.sin(-(k-1)*theta +d)
    return x, y

上記の関数を使ってグラフを描画する関数

notebook

def plot_orbit(R, Rt, k, n):
    """
    工具中心の軌道と、刃の軌道を描画
    """
    d=4 #描画範囲
    c=129 # データ数。適当で良い。
    _, ax = create_ax((d,-d),(d,-d)) # ax生成

    # ワーク一周分のデータを作成。
    theta = np.linspace(0, 2*np.pi, c) # c個のデータを、0-2πまで均等に生成

    x,y = circle_data(R, theta) #工具中心の軌道（円）。
    draw_data(ax,x,y) # 描画
    # 刃数nの分だけ軌跡を描画
    for i in range(n):
        x,y = poly_data(R, Rt, k, theta, n, i)
        draw_data(ax, x, y , color="red")

あとはパラメーターを設定して呼び出すだけ。

notebook

params ={
 "R":2, # ワークと工具中心の距離
 "Rt":1.5, # 工具の半径
 "k": 2, # 回転比
 "n":3, # 刃の数
}
plot_orbit(**params)

結果

パラメータを変化させた結果を確認します。
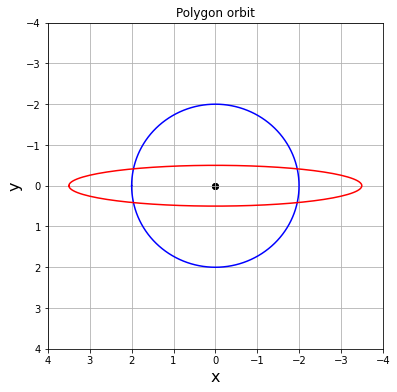
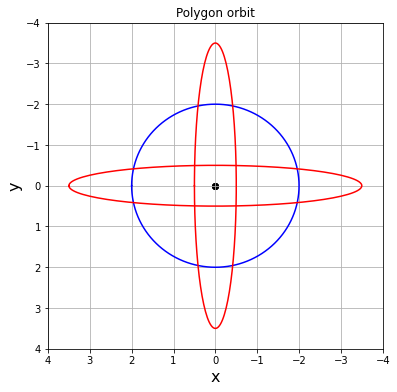
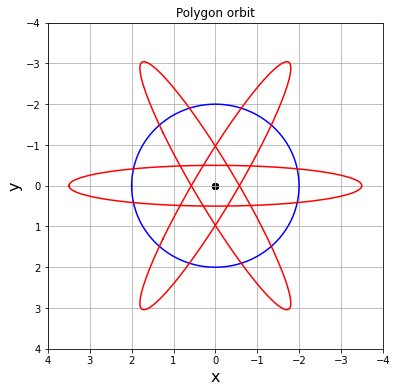
赤が刃の軌跡、青が工具中心の軌跡です。

k=2の場合

回転比2:1で固定して刃の数を増やして行った場合です。

k=2, n=1の場合:

k=2, n=2の場合:

k=2, n=3の場合:

赤が刃の軌跡なのでこの最内で切り取られた部分が切削面になります。
これらを見ると軌道は直線ということは無く、楕円（に似た）形のより平坦な箇所が切削面になっている様です。

その他

k=3, n=1とすると三角形もできそうです。これは凹型になります。

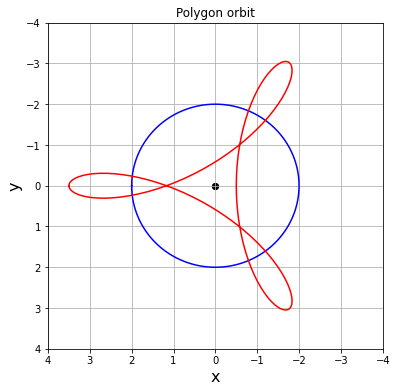
またR,Rtを変えても形が色々と変わります。

考察

刃の軌跡について

これをみると、刃は直線を描いているわけではなく、楕円（に似た）形の長辺部分が切削面となっています。厳密には直線ではないけど、用途によっては許される範囲の精度で加工ができる、ということの様です。
工具の半径が大きいとより直線に近づきます。

回転比kについて

上とも重複しますがk=2(回転比2:1)だと直線になる、と行った特別な意味は無い様です。
経験的に2:1が良いとされているのか、またはこの値が一番フラットに近くなるという結果が出ているのか、そこまでは調べきれていません。

奇数角形について

x角形を作るには x = k * n となる様にすると良いので、特にk=2に固定しなければ、奇数角形もできます。
三角形の場合は (k, n ) = (3,1), (1.5, 2）などの組み合わせが考えられます。
実用になるかは、この曲線が加工精度として許せるかどうかという事になるでしょうか。

まとめと雑感

• グラフで描画することにより、ポリゴン加工の動作がより直感的に理解できた気がします。
• 回転比2:1というのは、数学上の特別な値ではなく、加工において効率と精度をバランスよく実現するために採用された値だという理解です。
• 理屈上、k, n, R, Rtがわかれば、切削面が直線に対してどれくらい乖離するかを計算でき、加工する前に精度を計算可能だと思うのですが、現状そこまでは手が出せてません。

おまけ

より軌道を理解するため、アニメーション版も作ってみました。
が、微妙に動作しなかったりします。

notebook

%matplotlib nbagg
from matplotlib import animation

R=2
Rt=1.5
k=2
n=4

d=4 #描画範囲
c=129 # データ数
fig, ax = create_ax((d,-d),(d,-d))
x, y = [],[]
x_p = [[] for _ in range(n)]
y_p = [[] for _ in range(n)]

def _update(frame):
    ax.grid()
    x1,y1 = circle_data(R, frame)
    x.append(x1)
    y.append(y1)
    ax.plot(x, y, color="blue")
    for i in range(n):
        x1,y1 = poly_data(R,Rt,k,frame, n,i)
        x_p[i].append(x1)
        y_p[i].append(y1)
        ax.plot(x_p[i], y_p[i], color="red")

params= {
    "fig": fig,
    "func": _update,
    "interval": 20,
    "frames": np.linspace(0, 2*np.pi, c),
    "repeat":False,
}

anime = animation.FuncAnimation(**params)