はじめに
こんにちは!
この記事では、離散フーリエ変換(DFT)について解説していきます。
自分なりにまとめてみたので一読していただけると嬉しいです。
離散フーリエ変換とは
離散フーリエ変換とは、ディジタル信号データを解析する手法になります。
あるディジタル信号データを、「周期的なデータ」で「三角関数の無限和として表せる」と仮定した時に、それぞれの三角関数の「周波数」「振幅」「位相」を求めることができます。
また、この離散フーリエ変換は、連続の周期関数を三角関数の無限和として表すフーリエ級数展開を拡張したものであり、まず、フーリエ級数展開から解説していきます。
ちなみに、フーリエ変換は「非周期関数」を「周期が無限の周期関数」とみなしてフーリエ級数展開を拡張したものになります。
フーリエ級数展開の式
まず、以下の式がフーリエ級数展開の式になります。
\begin{align}
x(t) &= a_0 + \sum_{m=1}^{\infty}a_mcos\frac{2\pi m}{T}t + \sum_{m=1}^{\infty}b_msin\frac{2\pi m}{T}t\\
&= a_0\\
&\quad+a_1 cos\frac{2\pi}{T}t + b_1 sin\frac{2\pi}{T}t\\
&\quad+a_2 cos\frac{2\pi\times2}{T}t + b_2 sin\frac{2\pi\times2}{T}t\\
&\quad\cdots\\
&\quad+a_m cos\frac{2\pi\times m}{T}t + b_m sin\frac{2\pi\times m}{T}t\\
&\quad\cdots
\end{align}
上記の式は、x(t)を連続の周期関数、Tを周期として、正弦余弦の無限和で表した式になります。
また、
\left\{
\begin{array}{ll}
a_0 \sim a_\infty\\
b_1 \sim b_\infty
\end{array}
\right.\\
は、フーリエ係数となります。
また、最初のaは直流成分になります。
このフーリエ係数を求められれば、三角関数の無限和で周期関数を表すことができるので、以下にフーリエ係数の導出を示します。
三角関数の直交性
上記のフーリエ級数展開の式から、フーリエ係数を導出していきたいのですが、その前に必要な知識として、三角関数の直交系というものがありますので、以下に示します。
\left\{
\begin{array}{ll}
\int_{0}^{T} sin\frac{2\pi m}{T}t \times sin\frac{2\pi n}{T}tdt =
\left\{
\begin{array}{ll}
\frac{T}{2} & (m = n) \\
0 & (m \neq n)
\end{array}
\right.\\
\int_{0}^{T} cos\frac{2\pi m}{T}t \times cos\frac{2\pi n}{T}tdt =
\left\{
\begin{array}{ll}
\frac{T}{2} & (m = n) \\
0 & (m \neq n)
\end{array}
\right.\\
\int_{0}^{T} cos\frac{2\pi m}{T}t \times sin\frac{2\pi n}{T}tdt = 0
\end{array}
\right.\\
この三角関数の直交系を使えば簡単にフーリエ係数を導出できます!
フーリエ係数の導出
まず、あるフーリエ係数を求めるために、フーリエ級数展開の式の両辺にそのフーリエ係数にかかる三角関数をかけます。
今回はm番目のaを求めることにします。(bでも同様の手法で求められます。)
\begin{align}
x(t) cos\frac{2\pi m}{T}t
&= a_0 cos\frac{2\pi m}{T}t\\
&\quad+a_1 cos\frac{2\pi}{T}t cos\frac{2\pi m}{T}t + b_1 sin\frac{2\pi}{T}t cos\frac{2\pi m}{T}t\\
&\quad+a_2 cos\frac{4\pi}{T}t cos\frac{2\pi m}{T}t + b_2 sin\frac{4\pi}{T}t cos\frac{2\pi m}{T}t\\
&\quad\cdots\\
&\quad+a_m cos\frac{2\pi m}{T}t cos\frac{2\pi m}{T}t + b_m sin\frac{2\pi m}{T}t cos\frac{2\pi m}{T}t\\
&\quad\cdots
\end{align}
そして、両辺を0からTの間で積分します。
\begin{align}
\int_{0}^{T}x(t) cos\frac{2\pi m}{T}t dt
&= \int_{0}^{T}a_0 cos\frac{2\pi m}{T}tdt\\
&\quad+\int_{0}^{T}a_1 cos\frac{2\pi}{T}t cos\frac{2\pi m}{T}tdt + \int_{0}^{T}b_1 sin\frac{2\pi}{T}t cos\frac{2\pi m}{T}tdt\\
&\quad+\int_{0}^{T}a_2 cos\frac{4\pi}{T}t cos\frac{2\pi m}{T}t dt+\int_{0}^{T} b_2 sin\frac{4\pi}{T}t cos\frac{2\pi m}{T}tdt\\
&\quad\cdots\\
&\quad+\int_{0}^{T}a_m cos\frac{2\pi m}{T}t cos\frac{2\pi m}{T}tdt +\int_{0}^{T} b_m sin\frac{2\pi m}{T}t cos\frac{2\pi m}{T}tdt\\
&\quad\cdots
\end{align}
ここで先ほどの三角関数の直交性を思い出してください。
この積分で右辺に残るのは、
\int_{0}^{T}a_m cos\frac{2\pi m}{T}t cos\frac{2\pi m}{T}tdt = \frac{T}{2} a_m
だけになります。
よって、
a_m = \frac{2}{T} \int_{0}^{T}x(t) cos\frac{2\pi m}{T}tdt
となります。
同様に、
b_m = \frac{2}{T} \int_{0}^{T}x(t) sin\frac{2\pi m}{T}tdt
となります。
フーリエ級数展開を複素フーリエ級数展開に変形
一応、上記の状態でフーリエ級数展開の導出は終わりなのですが、実は三角関数のみを使った展開は数学的に取り扱いにくいらしいのです。
ですので、複素指数関数を用いた複素フーリエ級数展開をフーリエ級数展開から導出していきます。
また他にも、複素フーリエ級数展開で表すメリットがあり、
「展開式がきれいにまとまる。」
「フーリエ変換につながる。」
「周波数成分の振幅と位相が明示的に表現される。」
というメリットがあります。
x(t) = a_0 + \sum_{m=1}^{\infty}a_mcos\frac{2\pi m}{T}t + \sum_{m=1}^{\infty}b_msin\frac{2\pi m}{T}t\
オイラーの公式
\left\{
\begin{array}{ll}
\frac{e^{i\theta} + e^{-i\theta}}{2} = cos\theta\\
\frac{e^{i\theta} + e^{-i\theta}}{2i} = sin\theta\\
\end{array}
\right.\\
\bigl(
e^{i\theta} = cos\theta + isin\theta
\quad , \quad
e^{-i\theta} = cos\theta - isin\theta
\bigr)
より、
\begin{align}
x(t) &= a_0 + \sum_{m=1}^{\infty}\frac{a_m}{2}
\bigl(e^{\frac{i2\pi m}{T}t} + e^{\frac{-i2\pi m}{T}t}\bigr)
+\sum_{m=1}^{\infty}\frac{b_m}{2i}
\bigl(e^{\frac{i2\pi m}{T}t} - e^{\frac{-i2\pi m}{T}t}\bigr)\\
&=a_0 + \sum_{m=1}^{\infty}\frac{a_m - ib_m}{2}
e^{\frac{i2\pi m}{T}t}
+\sum_{m=1}^{\infty}\frac{a_m + ib_m}{2i}
e^{\frac{-i2\pi m}{T}t}\\
&=a_0 + \sum_{m=1}^{\infty}\frac{a_m - ib_m}{2}
e^{\frac{i2\pi m}{T}t}
+\sum_{m=-1}^{-\infty}\frac{a_{-m} + ib_{-m}}{2i}
e^{\frac{i2\pi m}{T}t}\\
&=a_0 + \sum_{m=1}^{\infty}\frac{a_m - ib_m}{2}
e^{\frac{i2\pi m}{T}t}
+\sum_{m=-1}^{-\infty}\frac{a_m + ib_m}{2i}
e^{\frac{i2\pi m}{T}t}\\
\end{align}
ここで、複素フーリエ係数
X_m = \frac{a_m - ib_m}{2}
と置くと、
\begin{align}
x(t) &= a_0 + \sum_{m=1}^{\infty}X_m
e^{\frac{i2\pi m}{T}t}
+\sum_{m=-1}^{-\infty}X_m
e^{\frac{i2\pi m}{T}t}\\
&= a_0 + \sum_{m=-\infty}^{\infty}X_m
e^{\frac{i2\pi m}{T}t}
\end{align}
となる。
また、フーリエ級数展開の
a_m = \frac{2}{T} \int_{0}^{T}x(t) cos\frac{2\pi m}{T}tdt\\
b_m = \frac{2}{T} \int_{0}^{T}x(t) sin\frac{2\pi m}{T}tdt
を用いて、
\begin{align}
X_m
&= \frac{a_m - ib_m}{2}\\
&=\frac{1}{T} \int_{0}^{T}x(t) cos\frac{2\pi m}{T}tdt -
i\frac{1}{T} \int_{0}^{T}x(t) sin\frac{2\pi m}{T}tdt\\
&=\frac{1}{T} \int_{0}^{T}x(t) e^{-i\frac{2\pi m}{T}t}dt\\
\end{align}
と、複素フーリエ係数を導出できる。
離散フーリエ変換の導出
ここまで来てやっと離散フーリエ変換の導出になります。
連続の周期関数についての複素フーリエ級数展開を、離散データに拡張することで導出します。
まず、受け取ったデータを周期関数の1周期分のデータと考えます。
そして、
データの総数を、N
サンプリング間隔を、Δt
とします。
そこから、
周期Tは、N×Δt
あるn個までの時間tは、n×Δt
と導出できます。
以上の変数を複素フーリエ級数展開の式に代入していきます。
また、連続から離散への拡張なので積分から総和に変換します。
そうすると以下の式から、
\begin{align}
X_m
&=\frac{1}{T} \int_{0}^{T}x(t) e^{-i\frac{2\pi m}{T}t}dt\\
\end{align}
以下の式になります。
\begin{align}
X_m
&=\frac{1}{N\Delta t} \sum_{n=0}^{N-1}x(n\Delta t) e^{-i\frac{2\pi m}{N\Delta t}n\Delta t}\Delta t\\
&=\frac{1}{N} \sum_{n=0}^{N-1}x(n\Delta t) e^{-i\frac{2\pi m}{N}n}\\
\end{align}
以上が離散フーリエ変換の導出になります。
離散フーリエ変換をpythonで実装して実験
import numpy as np
import matplotlib.pyplot as plt
import cmath
#サンプリング間隔
t = 0.1
x = np.arange(0, 2 * cmath.pi, t)
#振幅
a1 = 2
a2 = 1
#周波数
f1 = 2
f2 = 4
def y(x,a,f):
return a * np.sin(f*x)
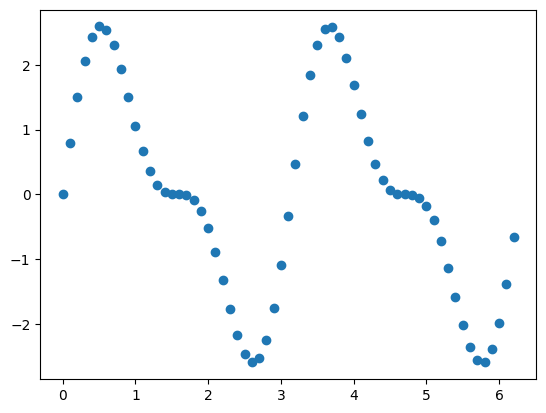
plt.scatter(x,y(x,a1,f1)+y(x,a2,f2))
この合成波を解析していきます。
X = []
N = len(x)
for m in range(10):
tmp_X = 0j
for n in range(N):
tmp_X += (y(n*t,a1,f1)+y(n*t,a2,f2)) * cmath.e**(-1j * 2 * cmath.pi * n * m / N)
tmp_X = np.abs(tmp_X)*2/N
X.append(tmp_X)
plt.scatter(np.arange(10),X)
plt.xlabel("周波数", fontname="MS Gothic")
plt.ylabel("振幅", fontname="MS Gothic")
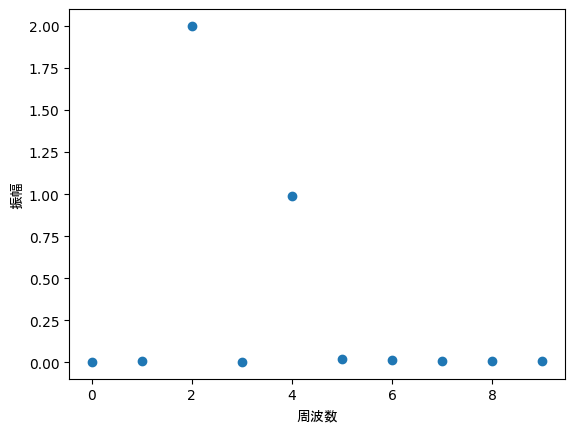
この結果を見ると、最初にプロットされた合成波が、
「周波数2で振幅2の波」と「周波数4で振幅1の波」
の合成波であることがわかります。
参考文献
https://tatamiya-practice.hatenablog.com/entry/2020/12/26/150306
https://www.itd-blog.jp/entry/voice-recognition-10
https://www.nli-research.co.jp/report/detail/id=69307?pno=2&site=nli
https://imagingsolution.net/math/fourier-transform/discrete-fourier-transform/
https://blog.mktia.com/discrete-fourier-transform-in-python/
https://kenyu-life.com/2019/06/07/complexfourierseries/
https://ja.wikipedia.org/wiki/%E3%83%95%E3%83%BC%E3%83%AA%E3%82%A8%E5%A4%89%E6%8F%9B
https://ja.wikipedia.org/wiki/%E9%9B%A2%E6%95%A3%E3%83%95%E3%83%BC%E3%83%AA%E3%82%A8%E5%A4%89%E6%8F%9B
https://rikeinotame.com/fourier1/
https://rikeinotame.com/fourier2/
https://rikeinotame.com/fourier3/
https://rikeinotame.com/dft1/
https://rikeinotame.com/dft2/