HSMAC法によるキャビティーフロー解析のJuliaコード

はじめに

HSMAC法（SOLA法）でキャビティーフローを解くためのコードをJuliaで作成しました。

[岡本 正芳「数値計算による流体力学- ポテンシャル流,層流,そして乱流へ -」コロナ社（2016）]
(https://www.amazon.co.jp/%E6%95%B0%E5%80%A4%E8%A8%88%E7%AE%97%E3%81%AB%E3%82%88%E3%82%8B%E6%B5%81%E4%BD%93%E5%8A%9B%E5%AD%A6-%E3%83%9D%E3%83%86%E3%83%B3%E3%82%B7%E3%83%A3%E3%83%AB%E6%B5%81-%E5%B1%A4%E6%B5%81-%E3%81%9D%E3%81%97%E3%81%A6%E4%B9%B1%E6%B5%81%E3%81%B8/dp/4339046515)
にあるFortranによるHSMAC法のコードを参考にしました。

補足

計算のリスタートができるようにしたコードをGithubにおきました。
https://github.com/ishigakim/2Dcavity.git

コード概要

• 2次元のキャビティーフローの解析コード。
• 圧力解法にはHSMAC法。
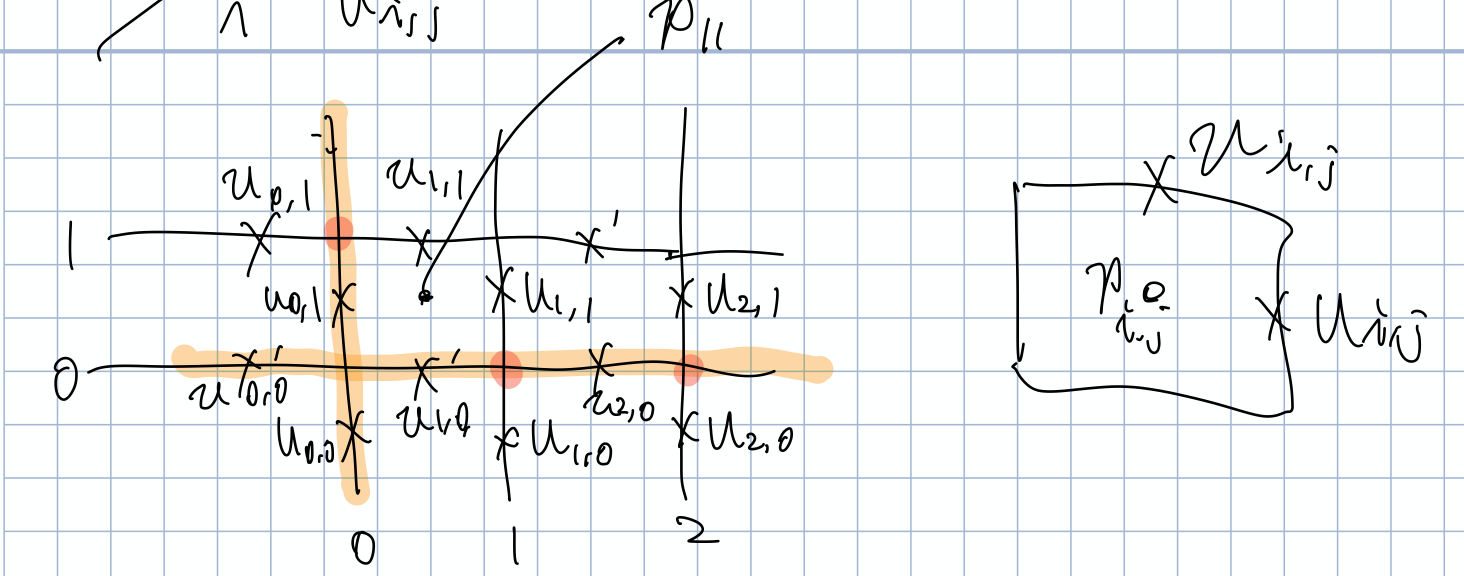
• スタッガード格子を用いており，セル中心に圧力，uはセルの右側のフェイス，vはセルの上側のフェイスで定義。
• スタッガード格子でu, vの位置がずれているので，境界条件には中点で速度0になるような条件が出てくる。
• デフォルト設定では40x40の格子で，Reynolds数=100を計算。正方形領域で上側の境界(y=1)でu=1とする。それ以外の境界ではすべりなし。

物理量の配置の模式図。オレンジのところが速度0の滑りなし条件の箇所。薄い赤のところでuもしくはvが0になるようにu_{i,0}等の条件を設定する。ちなみにJuliaのコードではインデックスが1から始まる都合で，図と添字がずれます。

Juliaコード

ソルバ

using Parameters
using PyPlot
using BenchmarkTools
using HDF5

@with_kw struct Param{T1,T2}
    dt::T1 = 0.01
    nu::T1 = 1e-2
    U::T1 = 1.0
    nstep::T2 = 200
    omega::T1 = 1.7
    # max iteration no. of inner iteration
    niter::T2 = 50000
    
    nx::T2 = 40
    ny::T2 = 40
    
    # length
    Lx::T1 = 1.0
    Ly::T1 = 1.0
    dx::T1 = Lx/nx
    dy::T1 = Ly/ny
   
    ndata::T2 = 50
     
    outfile::String = "uv" 

end

function main(para)
    @unpack nx, ny, nstep, ndata = para
    # velocity
    u = zeros(Float64, nx+2, ny+2)
    v = zeros(Float64, nx+2, ny+2)
    # auxiliary velocity
    ua = zeros(Float64, nx+2, ny+2)
    va = zeros(Float64, nx+2, ny+2)
    # pressure, corrected pressure
    pa = zeros(Float64, nx+2, ny+2)
    pc = zeros(Float64, nx+2, ny+2)
    # coordinate
    x = zeros(Float64, nx+1, ny+1)
    y = zeros(Float64, nx+1, ny+1)
    
    uo = zeros(nx+1, ny+1)
    vo = zeros(nx+1, ny+1)
    uxy = zeros(nx+1, ny+1)
    vxy = zeros(nx+1, ny+1)
    div = zeros(Float64, nx+2, ny+2)
    
    init(para, x, y)
    BC(para, u, v)
    for n = 1:nstep
        solveV(para, u, v, ua, va, pa, uo, vo, uxy, vxy)
        SOLA(para, n, u, v, ua, va, pa, pc, div)
        if n%ndata == 0
            #output(para, n, u, v, pa, x, y)
            #println("u[20,20]=",u[21,21])
        end
    end
end

function init(para, x, y)
    @unpack nx, ny, dx, dy = para
    
    for j in 2:ny+1
        for i in 2:nx+1
            x[i,j] = (i-2+0.5)*dx
        end
    end
    for j in 2:ny+1
        for i in 2:nx+1
            y[i,j] = (j-2+0.5)*dy
        end
    end
end

function BC(para, u, v)
    @unpack nx, ny, U = para
    
    for i=1:nx+2
        u[i, ny+2] = 2.0U - u[i, ny+1]
        v[i, ny+1] = 0.0
        u[i, 1] = -u[i, 2]
        v[i, 1] = 0.0
    end
    for j=1:ny+2
        u[nx+1, j] = 0.0
        v[nx+2, j] = -v[nx+1, j]
        u[1, j] = 0.0
        v[1,j] = -v[2, j]
    end
    #println("BC",u[nx-1:nx+2,ny-1:ny+2])
end

function solveV(para, u, v, ua, va, pa, uo, vo, uxy, vxy)
    @unpack dt, nu, dx, dy, nx, ny, U = para

    for j=2:ny+1
        for i=2:nx+1
            uo[i,j] = (u[i,j] + u[i-1,j])*0.5
            vo[i,j] = (v[i,j] + v[i,j-1])*0.5
            uxy[i,j] = (u[i,j+1] + u[i,j])*0.5
            vxy[i,j] = (v[i+1,j] + v[i,j])*0.5
        end
    end    
    
    for j=2:ny+1
        for i=2:nx
            ua[i,j] = u[i,j] + dt*(
                -(uo[i+1,j]^2 - uo[i,j]^2)/dx
                -(uxy[i,j]*vxy[i,j] - uxy[i,j-1]*vxy[i,j-1])/dy
                + nu*(u[i+1,j] -2.0u[i,j] + u[i-1,j])/dx^2
                + nu*(u[i,j+1] -2.0u[i,j] + u[i,j-1])/dy^2
                - (pa[i+1,j] - pa[i,j])/dx
                )
        end
    end
    
    for j=2:ny
        for i=2:nx+1
            va[i,j] = v[i,j] + dt*(
                -(uxy[i,j]*vxy[i,j] - uxy[i-1,j]*vxy[i-1,j])/dx
                -(vo[i,j+1]^2 - vo[i,j]^2)/dy
                + nu*(v[i+1,j] -2.0v[i,j] + v[i-1,j])/dx^2
                + nu*(v[i,j+1] -2.0v[i,j] + v[i,j-1])/dy^2
                - (pa[i,j+1] - pa[i,j])/dy
                )
        end
    end
    BC(para, ua, va)
    
    #println("solveV", ua[nx-1:nx+2,ny-1:ny+2])
end

function SOLA(para, n, u, v, ua, va, pa, pc, div)
    @unpack dt, nu, dx, dy, nx, ny, niter, omega = para
    
    for m=1:niter
        divmax::Float64 = 0.0
        for j=2:ny+1
            for i=2:nx+1
                div[i,j] = (ua[i,j] - ua[i-1,j])/dx + (va[i,j] - va[i,j-1])/dy
                divmax = max(abs(div[i,j]), divmax)
                pc[i,j] = - omega*div[i,j]/dt/(1.0/dx^2 + 1.0/dy^2)*0.5
                ua[i,j] = ua[i,j] + dt/dx*pc[i,j]
                ua[i-1,j] = ua[i-1,j] - dt/dx*pc[i,j]
                va[i,j] = va[i,j] + dt/dy*pc[i,j]
                va[i,j-1] = va[i,j-1] - dt/dy*pc[i,j]
                pa[i,j] = pa[i,j] + pc[i,j]
            end
        end    
        if divmax <= 1e-8
            if n%100 == 0
                println("divmax=", divmax)
                println("iter, max/min div=", m, ", ", findmax(abs.(view(div,2:nx+1, 2:ny+1))), ", ", findmin(abs.(view(div,2:nx+1, 2:ny+1))))
            end
            break
        end
    end
    
    for j=2:ny+1
        for i=2:nx
            u[i,j] = ua[i,j]
        end
    end
    for j=2:ny
        for i=2:nx+1
            v[i,j] = va[i,j]
        end
    end
    BC(para, u, v)
    
    #println("sola",u[nx-1:nx+2,ny-1:ny+2])
end

function output(para, n, u, v, pa, x, y)
    @unpack outfile, dt, nx, ny = para
    time = string(dt*n)
    println("time=", time)
    filename = outfile*time*".h5"
    h5open(filename, "w") do file
        write(file, "u", (u[2:nx+1, 2:ny+1]+u[1:nx, 2:ny+1])/2)
        write(file, "v", (v[2:nx+1, 2:ny+1]+v[2:nx+1, 1:ny])/2)
        write(file, "pa", pa[2:nx+1, 2:ny+1])
        write(file, "x", x[2:nx+1, 2:ny+1])
        write(file, "y", y[2:nx+1, 2:ny+1])
    end
    
    #open( outfile*time*".csv", "w")　 do f
    #    println(f, "x, y, u, v, pa")
    #    for j=2:ny+1
    #        for i=2:nx+1
    #            println(f, x[i,j], ",", y[i,j], ",",(u[i,j]+u[i-1,j])/2., ",", (v[i,j]+v[i,j-1])/2.0, ", ", pa[i,j] )
    #        end
    #    end
    #end
end

• Paramで計算のパラメータを設定
• main中に計算で使う配列を定義。
• initが初期条件設定。BCが境界条件設定。
• solveVが予測速度の計算。SOLAでdivV=0になるように反復計算を実行。速度を修正。
• output，HDF5でデータ保存。CSVで保存したいときはコメントアウト部分を復活させる。

計算

para = Param(nstep=2000, ndata=100, )
@btime main(para)
10.418 s (13370 allocations: 1.13 MiB)

• Paramでパラメータを与える。
• ちなみに参考にしたFotranではgfotranつかって，　実行に25秒くらい。 実行に15秒くらい。Juliaのほうが早い。（Juliaのほうが早いのは早いですが，Fotranのほうの条件間違ってました。Intel FortranだとFortranのほうが少し早いくらいです）
• 環境2.3 GHz Quad-Core Intel Core i5, メモリ16 GB 2133 MHz LPDDR3，MacBook Pro (13-inch, 2018, Four Thunderbolt 3 Ports)

実行時のメモリアロケーションが13370 allocationsとなってるが，途中にあるprintが原因。途中にprintによる結果出力をなくせば，最初の配列の宣言の分だけになる（13 allocationになる）。

ポスト処理

filename = "uv10.0.h5"
file = h5open(filename, "r") 
u = read(file, "u")
v = read(file, "v")
x = read(file, "x")
y = read(file, "y")
pa = read(file, "pa")
close(file)

X = x[:,1]
Y = y[1,:]
fig = plt.figure(figsize = (15, 13))
ax1 = fig.add_subplot(221)
heatmap = ax1.contour(X', Y, u', cmap="jet", levels=15 )
fig.colorbar(heatmap, ax=ax1)
ax2 = fig.add_subplot(222)
heatmap2 = ax2.contour(X', Y, v', cmap="jet", levels=15)
fig.colorbar(heatmap2, ax=ax2)

ax3 = fig.add_subplot(223)
umag = sqrt.(u.*u .+ v.*v)
# image = ax3.quiver(x[:, 20:40], y[:, 20:40], u[:, 20:40], v[:, 20:40], umag, scale=4, cmap="jet")
image = ax3.quiver(x[:, :], y[:, :], u[:,:], v[:, :], umag, scale=2, cmap="jet")
# image = ax3.streamplot(x', y', u, v)
cb=fig.colorbar(image, ax=ax3)

ax4 = fig.add_subplot(224)
heatmap3 = ax4.contour(X', Y, pa', cmap="jet", levels=15)
fig.colorbar(heatmap3, ax=ax4)

fig = plt.figure(figsize = (5,5))
ax1 = fig.add_subplot(111)
image = ax1.streamplot(x'[:, :], y'[:, :], u'[:,:], v'[:, :], color=u, cmap="jet")

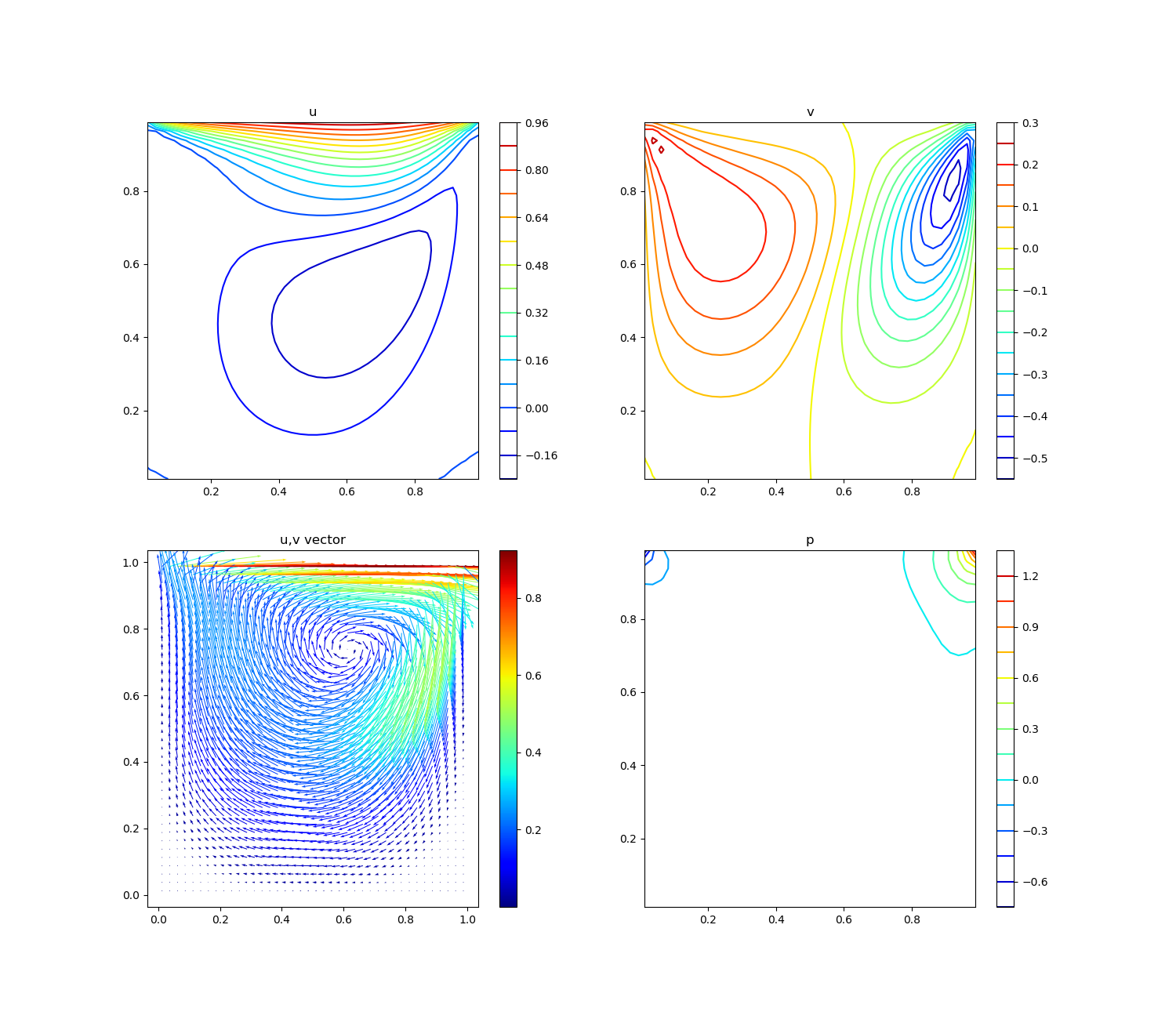
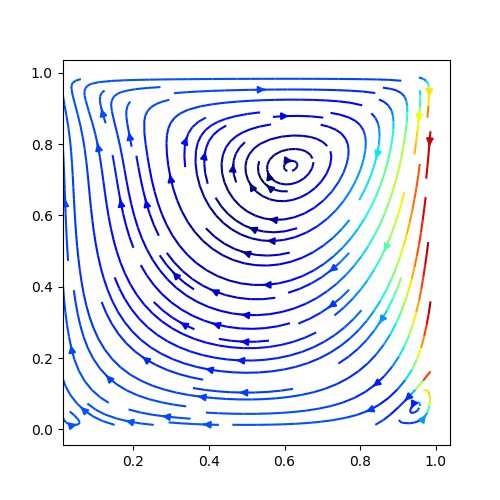
• 速度コンター，速度ベクトル，圧力コンター，流線を書くコード。

最後

見本のコードがあって，それをうつしただけなのに，まともに動かすのに1日かかりました。途中で変数を間違えていて，計算がうまくいかなくなっているのを，発見するのにだいぶてこずりました。

適宜境界条件を変えれば，他の計算もできます。

付録

ないよりはあったほうがましかな程度の式のメモ書き。