概要

コインを100枚投げたときに表が出る枚数は、どのくらいだと思いますか？
数式を使えば、簡単に計算できますが、せっかくコンピュータがあるので（？）ブラウザ上で疑似的にコインを投げて実験します。また、その結果をchart.jsを用いて棒グラフで表示したいと思います。

使用技術

HTML
JavaScript
chart.js 2.9.4

プログラム

今回紹介する範囲としては、メインのJavascriptの処理部分を説明します。HTML部分は、説明がややこしくなるため割愛します。ご了承ください。

ベルヌーイ試行の関数

ベルヌーイ試行とは、「成功」または「失敗」のように２種類のみの結果しか得られない実験のことです。今回は、コインが表になった場合に成功とみなして処理する関数を作成しました。

/**
 * ベルヌーイ試行
 * @param {number} p 確率 (0.0 ~ 1.0)
 * @return {boolean} true:成功, false:失敗
 */
const bernoulliTrial = (p) => Math.random() < p;

二項分布の関数

二項分布とは、ベルヌーイ試行をn回行った場合に、事象が何回起こるかの確率分布です。
下記関数は、コインを投げた回数をnとして、コインが表になった回数をカウントして返します。

/**
 * 二項分布
 * @param {number} n 試行回数
 * @param {number} p 確率 (0.0 ~ 1.0)
 * @return {number} 成功した回数
 */
const binomialDistribution = (n, p) => {
    let count = 0;
    for (let i = 0; i < n; i++) {
      if (bernoulliTrial(p)) count++;
    }
    return count;
}

グラフに表示するデータを作成

二項分布の関数を複数回実行し、グラフに表示するデータを生成します。コインが表になる確率は、50%を設定しています。

/**
 * グラフ表示用のデータを作成する
 * @param {number} trialCount 試行回数
 * @param {number} coinTossCount コイントスの回数
 * @return {array} [ラベルの配列,データの配列]
 */
const createData = (trialCount,coinTossCount) => {
    const graphData = Array(coinTossCount+1).fill(0);
    let count = 0;

    // データ表示用のラベルを生成する
    const labelsArray = [...Array(coinTossCount+1)].map((_, i) => i);

    // コイントスを実際に行い二項分布のデータを生成する
    for (let i=0; i<trialCount; i++) {
        count = binomialDistribution(coinTossCount, 0.5);
        graphData[count] = graphData[count] + 1
    }

    // 結果を返却
    return [labelsArray,graphData]
}

グラフの表示設定


// 試行回数
let trialCount = 100;
// コインを一回に投げる枚数
let coinTossCount = 100;
// グラフに表示するデータ
let [labelsArray,data] = createData(trialCount,coinTossCount);
// グラフの設定
const ctx = document.getElementById('mychart');
const myChart = new Chart(ctx, {
    type: 'bar',
    data: {
        labels: labelsArray,
        datasets: [{
            data: data,
            backgroundColor: "#ff9800"
        }]
    },
    options: {
        legend: {
            display: false,
        },
        scales: {
            xAxes: [{
                scaleLabel: {
                    display: true,
                    labelString: "コインを"+ coinTossCount +"回投げた時に表になった数回"
                },
            }],
            yAxes: [{
                scaleLabel: {
                    display: true,
                    labelString: "事象の回数"
                }
            }],
        }
    }
});

完成したもの

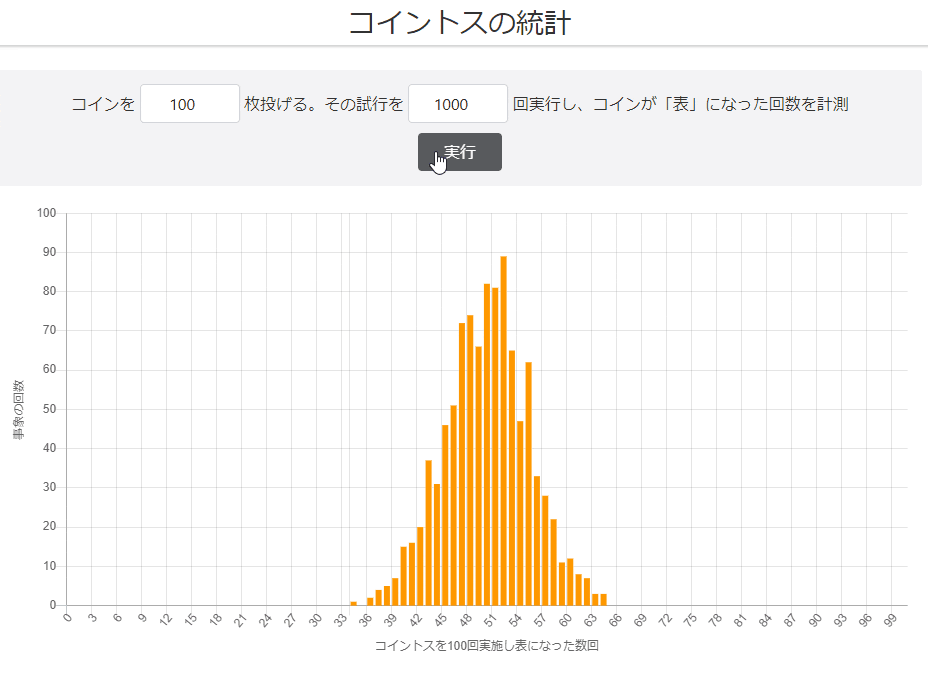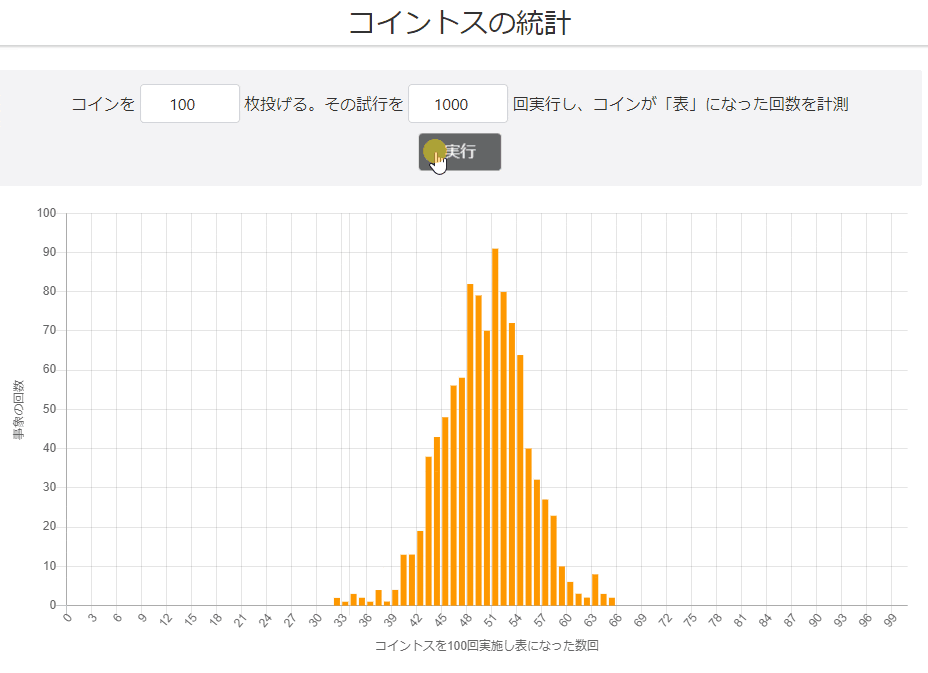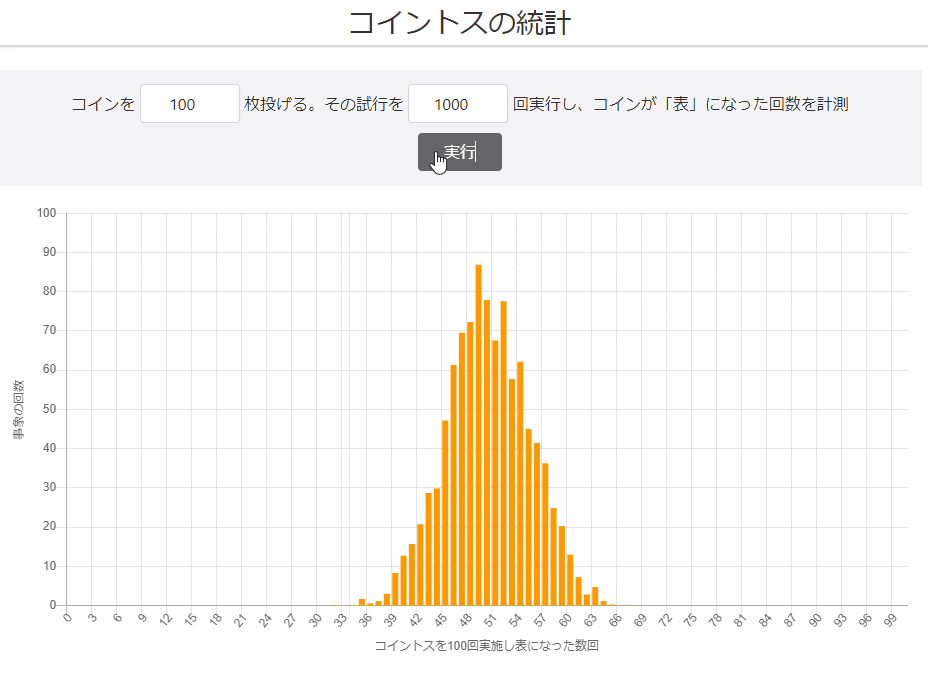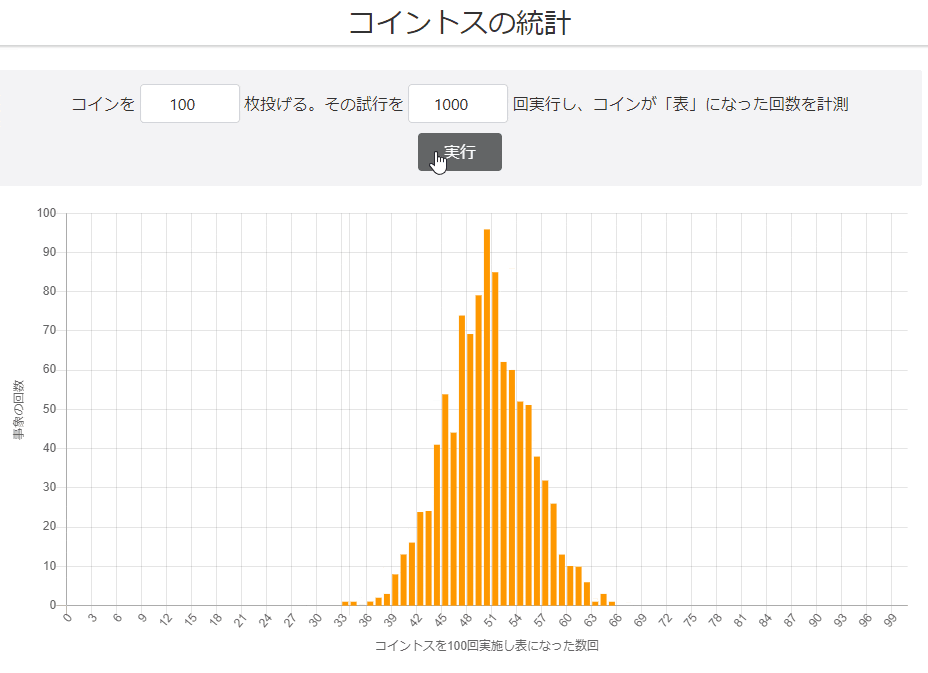
試行回数100回

結果が分散してしまっていますが、50回付近に集中していることが分かりますね。

試行回数1,000回

グラフの形がきれいになってきました

試行回数10万回

試行回数10万回だと、確率が収束してきて、きれいなグラフの形を維持できるようになりました。（そしてブラウザが頑張ってくれました！！）

おまけ

表の確立が80%の八百長コインだったら

ちゃんと80回付近に集中してますね。

おわりに

今回は、コインを100枚投げたときに表が出る枚数をchert.jsを用いて作成してみました。

プログラムでこのようなシミュレーションができると、「コイン枚数」や「試行回数」や「コインの表になる確率」を簡単に変更しシミュレーションができるのが面白いですね。

コードはgithubに公開しているので興味があったらどうぞ！

実際に動く画面もどうぞ！！

ここまで読んでいただきありがとうございました。

JavaScriptでコインを100枚投げたときに表が出る枚数をグラフで表示

概要