シルバーウィークだ!暗号だ!
ということで、Kotlinでエニグマを実装して遊んでみました。
エニグマとは
第二次世界大戦でナチス・ドイツが用いたローター式暗号機。
3枚のローターとリフレクター、プラグボードによって、入力されたアルファベットを別のアルファベットに置き換えることができる。
特徴
- 回転機構
一文字入力するごとにローターが回転して設定が変わるので、例えば「AAAA」と連続して同じ文字を入力しても、「LRPJ」といった具合に、別の文字に変わる。 - 「鍵」はローターの設定とプラグボードの配線
暗号における「鍵」の部分はローターの設定とプラグボードの配線である。
同じ設定なら、同じ暗号文が生成される。 - 反転性
暗号機と復元機を兼ねることができた。
例えば、「HELLO WORLD」と平文を入力して、「BQGWN GMBCR」と暗号化されたとする。
同じ鍵(設定)で「BQGWN GMBCR」と入力すると、「HELLO WORLD」が復元される。
モデル化してみる
これからKotlinでコーディングするにあたって、エニグマの仕組みをモデル化していきます。
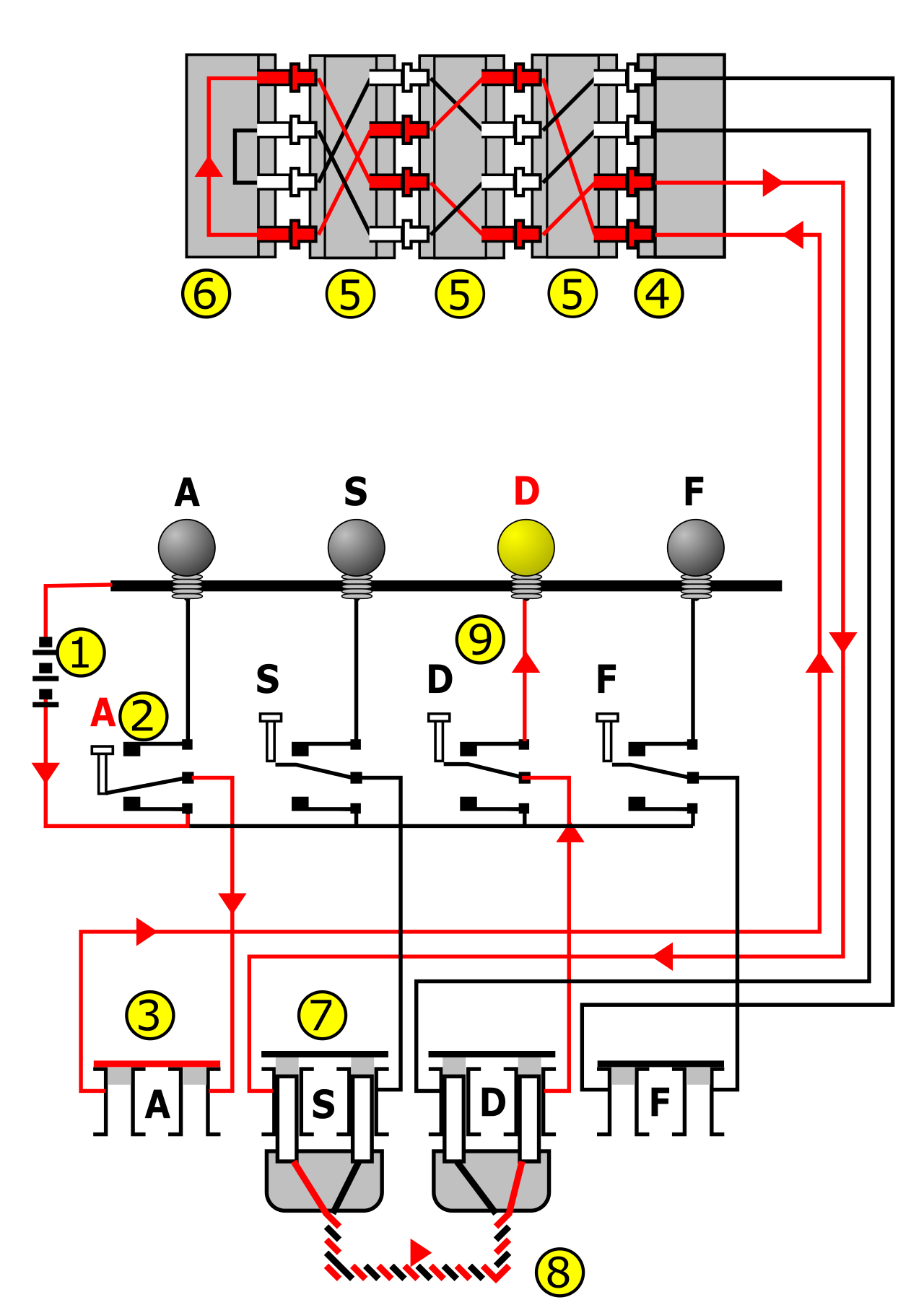
※Wikipediaより引用
エニグマの中身は3枚のローターとリフレクター、プラグボードです。
暗号化によって、アルファベットを別のアルファベットに置き換える操作は、関数(写像)として見ることができそうですね。
入力(Char)-> プラグボード -> ローターA -> ローターB -> ローターC -> リフレクター -> ローターC -> ローターB -> ローターA -> プラグボード -> 出力(Char)
というふうに、Charに対する関数の連鎖、メソッドチェーンとして表現するのが自然なように思います。
ローターやプラグボードは換字機に当たるので、換字表を生成するオブジェクトとして作成するのが良さそうです。
実装
まず換字表をどう表現するかを考えます。
各ローターやプラグボードは1対1に文字を変換させるので、Aは何に変わるか、Bは何に変わるか...を表にすれば良さそうですね。
そして、文字の変換は、Charに数値を足す計算で表すことができそうです。
[4, 2, 3...] // Aは4を足す、Bは2を足す、Cは3を足す...
上のリストでは、各アルファベットに何を足すかを表しており、Aは4つ足してEに、Bは2つ足してDに、Cは3つ足してFにといった具合に表現しています。
Zを超えて足された分については、modをとってAからまた戻るように考えましょう。
今後、このリストを「シフト表」と呼ぶことにします。
Charの拡張関数を書きます。
fun Char.shift(shifts: List<Int>): Char = let {
val position = it.uppercaseChar().code - 65
((position + shifts[position]) % 26 + 65).toChar()
}
「シフト表」を受け取って変換を行い、変換後の新しいCharを返す関数です。
変換結果がZをオーバーしたらAに戻るように、%26しています。
新しいCharを返り値で返すので、メソッドチェーンすることができるようになっています。
エニグマ本体について書いていきます。
package enigma
data class Enigma(
val rotor1: Rotor,
val rotor2: Rotor,
val rotor3: Rotor,
val reflector: Reflector,
val plugBoard: PlugBoard
)
エニグマを表すデータクラスです。
3つのローターとリフレクター、プラグボードを備えています。
これらの本質はシフト表の作成です。
シフト表を生成するオブジェクトとして、ローターを実装していきます。
まずはローターの中身になるスクランブラー。
val scramblerA = mapOf(
'A' to 'X',
'B' to 'H',
'C' to 'M',
'D' to 'V',
'E' to 'A',
...
読みやすく編集しやすいように、Aはどの文字に変わるか、Bはどの文字に変わるか、をマップで定義します。
次にロータークラス。
package enigma
import kotlin.math.pow
// ロータークラス
class Rotor(scrambler: Map<Char, Char>, initialRotate: Int, rotateBias: Int) {
private val rotateBias: Int
private var scrambler: List<Pair<Int, Int>>
private var stepCount = 0
init {
// ローターの回転バイアス
this.rotateBias = rotateBias
// コンストラクタの引数で受け取ったスクランブラーを、シフト表に整形する
val forward = scrambler.map { calcShift(it.key, it.value) }
val reflect = scrambler
.toSortedMap { a, b -> scrambler[a]!! - scrambler[b]!! }
.map { calcShift(it.value, it.key) }
this.scrambler = forward.zip(reflect) { a, b -> Pair(a, b) }
// 初期回転位置まで回転
for (i in 1..initialRotate) {
_rotate()
}
}
// 前半部分のシフト表を取得
fun getForwardShifts(): List<Int> = scrambler.map { it.first }
// 後半部分のシフト表を取得
fun getReflectShifts(): List<Int> = scrambler.map { it.second }
private fun _rotate() {
scrambler = scrambler.drop(1) + scrambler[0]
}
// ローターの回転処理
fun rotate() {
stepCount++
if ((stepCount / 26.0.pow(rotateBias.toDouble())) >= 1.0) {
_rotate()
stepCount = 0
}
}
}
fun calcShift(a: Char, b: Char): Int {
val diff = b.code - a.code
return when (diff >= 0) {
true -> diff
false -> diff + 26
}
}
初期設定として、スクランブラーと初期回転位置、回転バイアスをコンストラクタで受け取ります。
スクランブラーは内部でシフト表に変換して保持し、getメソッドで外部に提供できるようにします。
前半後半で必要なシフト表が逆になるので、それぞれ保管しております。
回転バイアスはローターの回転制御のためで、0なら1ステップで1、1なら26ステップで1、2なら26 * 26ステップで1目盛り回転します。
同じようにリフレクターとプラグボードも作成します。
class Reflector {
private val shifts: List<Int> = reflector.map { calcShift(it.key, it.value) }
fun getShifts(): List<Int> = shifts
}
class PlugBoard(shiftMap: Map<Char, Char>) {
private val shifts: List<Int>
init {
val tmpMap = plane.toMutableMap()
for (map in shiftMap) {
tmpMap[map.key] = map.value
tmpMap[map.value] = map.key
}
shifts = tmpMap.map { calcShift(it.key, it.value) }
}
fun getShifts(): List<Int> = shifts
}
これで必要なパーツは揃ったので、暗号化部分の関数を書きます。
package enigma
fun encrypt(char: Char, enigma: Enigma): Char = enigma.run {
char
.shift(plugBoard.getShifts())
.shift(rotor1.getForwardShifts())
.shift(rotor2.getForwardShifts())
.shift(rotor3.getForwardShifts())
.shift(reflector.getShifts())
.shift(rotor3.getReflectShifts())
.shift(rotor2.getReflectShifts())
.shift(rotor1.getReflectShifts())
.shift(plugBoard.getShifts())
.also {
rotor1.rotate()
rotor2.rotate()
rotor3.rotate()
}
}
エニグマの暗号化処理を、メソッドチェーンで表現できました!
Charに対する関数適用の連続という点で、本質を捉えられているのではないでしょうか。
最後にメイン関数です。
import enigma.*
fun main() {
// 各パーツを初期化
val rotor1 = Rotor(scramblerA, 1, 0)
val rotor2 = Rotor(scramblerB, 5, 1)
val rotor3 = Rotor(scramblerC, 20, 2)
val reflector = Reflector()
val plugBoard = PlugBoard(mapOf('H' to 'X', 'A' to 'E', 'O' to 'J'))
val enigma = Enigma(rotor1, rotor2, rotor3, reflector, plugBoard)
val message = "HELLO WORLD"
// 暗号化
val cypher = message
.split(" ")
.joinToString(" ") { m ->
m.toCharArray()
.map { encrypt(it, enigma) }
.toCharArray()
.concatToString()
}
println(cypher)
}
エニグマの鍵であるローターとプラグボードの設定が、初期化時に渡せています。
ここの設定を任意に組み替えることで、自由に暗号文を作れるでしょう。
ソースコード全文は以下のGitHubに公開しています。
https://github.com/iroha1203/Enigma
次はこのエニグマのロジックを使ってWEBアプリを作りたいですね。
それではまた!