![]()
![]() 本記事はClassi Advent Calendar 2020 17日目の記事です
本記事はClassi Advent Calendar 2020 17日目の記事です![]()
![]()
こんにちは。classi データAI部 Pythonエンジニアの @irisu-inwl です!
皆さん、数学は好きですか? 自分は大好きです。
日頃の数学のお供にwolfram alphaを使って代数計算を行ったり、最近ですと、社内勉強会でcolab+sympyを使って代数計算を行う機会が多いです。
本記事ではsympyを使ってどのような計算ができるのかを紹介します。
環境
Google Colabratory
colab環境にはsympyがインストール済みなので環境準備などせずとも使えます。
コード: https://colab.research.google.com/drive/1cOfjJtYuFYyY5BkX1gPwnje-bOdjbtdB?usp=sharing
Sympyってなに?
sympyとはpythonの数式処理ライブラリです。
公式サイト: https://docs.sympy.org/latest/index.html#
数式処理(Computer Algebra, Symbolic Computation)とは、$\sqrt{2}$や$e,\pi$といった数や変数を近似値ではなく記号そのままとして処理する分野です。
数式処理の有名な応用例として、東ロボプロジェクトの数学チームでの活用などがあります。
実際に、pythonのsqrtとの比較を見てみましょう。
from sympy import sqrt
from math import sqrt as sqrt_std
print(f'sympyのsqrt: {sqrt(2)**2}')
print(f'python標準のsqrt: {sqrt_std(2)**2}')
出力:
sympyのsqrt: 2
python標準のsqrt: 2.0000000000000004
このように、sympyでは$\sqrt{2}^2=2$が得られる対象として$\sqrt{2}$を出力しており、pythonの標準sqrt関数は$\sqrt{2}$の近似値を返しております。
次のように平方根同士の足し算や掛け算もできます。
from sympy import simplify
sympy_result = simplify((sqrt(2)+sqrt(3))**2)
std_result = (sqrt_std(2)+sqrt_std(3))**2
print(f'sympyのsqrt: {sympy_result}')
print(f'python標準のsqrt: {std_result}')
出力:
sympyのsqrt: 2*sqrt(6) + 5
python標準のsqrt: 9.898979485566358
sympyでは、$(\sqrt{2}+\sqrt{3})^2 = 2\sqrt{6}+5$が導かれました。
symplifyは数式を単純化(simplification)する関数です。(cf: https://docs.sympy.org/latest/tutorial/simplification.html?highlight=simplify)
方程式・恒等式の問題を解いてみよう!
sympyで高校数学レベルの代数の問題をsympyを用いて解いてみます。
2次方程式の解の公式
解の公式をsympyで求めてみましょう。
すなわち、$ax^2+bx+c = 0$の解が$x=\frac{-b \pm\sqrt{b^2-4ac}}{2a}$を示します。
from sympy import symbols, solve
a,b,c,x = symbols('a b c x')
solve(a* (x**2) + b * x + c, x)
出力:
[(-b + sqrt(-4*a*c + b**2))/(2*a), -(b + sqrt(-4*a*c + b**2))/(2*a)]
まず、変数として扱う文字をsymbolsで定義します。ここでは、a,b,c,xが変数となります。
次に$ax^2+bx+c=0$を$x$について解きます。solveを使うことで、第一引数に式$=0$を第二引数で指定した変数で解くことができます。
これよって、出力として、二つの解$\frac{-b+\sqrt{-4ac+b^2}}{2a},-\frac{b+\sqrt{-4ac+b^2}}{2a}$が得られました。
式を展開する
式の展開をsympyでやってみましょう。expand関数で式を展開できます。
from sympy import expand
x = symbols('x')
expand((x+1)*(x+2))
出力:
x**2 + 3*x + 2
ちょっと高度な恒等式をsympyを使って証明してみましょう。
(a^2+b^2)(c^2+d^2) = (ac-bd)^2+(ad+bc)^2
を証明してみます。
参考: https://mathtrain.jp/equality
from sympy import expand
a,b,c,d = symbols('a b c d')
expr1 = expand((a**2+b**2)*(c**2+d**2))
expr2 = expand((a*c-b*d)**2+(a*d+b*c)**2)
expr1 == expr2
出力:
True
これによって、左辺と右辺が式展開により等しい式であることが証明されました。
多項式の因数分解
多項式の因数分解をしてみましょう。
$x^2+5x+6=(x+2)(x+3)$を示してみます。
from sympy import factor
x = symbols('x')
factor(x**2 + 5*x + 6)
出力
(x + 2)*(x + 3)
sympyでは、factorを使うことで、多項式の因数分解をすることが出来ます。
2変数多項式でも簡単に因数分解をすることができます。
x,y = symbols('x y')
factor(2*x**2 + 5*x*y + 7*x + 2*y**2 + 5*y + 3)
出力
(x + 2*y + 3)*(2*x + y + 1)
このように高校数学で出てくる代数の題材をpythonで容易に扱うことが出来ます。
pythonを勉強してる高校生や数学の先生が数学を接する際に補助的に活用することなどが考えられそうです。
線形代数の問題を解いてみる。
少し進んだ線形代数の問題を解いてみましょう。
線形方程式を解く
sympyでは線形方程式も解けます。
たとえば、以下の線形方程式を解いてみましょう
\begin{align}
x+2y+3z = 1 \\
y+2z = 2 \\
z = 3
\end{align}
\iff
\left(
\begin{array}{lll}
1 & 2 & 3 \\
0 & 1 & 2 \\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{l}
x \\
y \\
z
\end{array}
\right)=\left(
\begin{array}{l}
1 \\
2 \\
3
\end{array}
\right)
これは後退代入により、3行目から$z=3$が得られ、2行目のzに代入し、$y=-2$が得られ、最後に$x=0$が得られます。
sympyではlinsolveとmatrixを使って解くことができます。
linsolveは引数に左辺の係数行列($Ax=b$の$A$の部分)と右辺のベクトル($Ax=b$の$b$の部分)をタプルで指定することで線形方程式を解くことが出来ます。
from sympy import Matrix, linsolve
x,y,z = symbols('x y z')
M = Matrix([
[1,2,3],
[0,1,2],
[0,0,1]
])
u = Matrix([[1,2,3]]).T
system = M, u
linsolve(system, x, y, z)
出力
{(0, -4, 3)}
また、線形方程式を表現する行列が正方行列でなくても解くことが出来ます。
次の連立方程式を解いてみましょう。
\left(
\begin{array}{lll}
2 & 0 & 0 \\
0 & 1 & 0 \\
4 & 0 & -1 \\
0 & 1 & -1
\end{array}
\right)
\left(
\begin{array}{l}
x \\
y \\
z
\end{array}
\right)=\left(
\begin{array}{l}
2 \\
1 \\
4 \\
1
\end{array}
\right)
これもlinsolveを用いることで解くことが出来ます。
x,y,z = symbols('x y z')
M = Matrix([
[2,0,4,0],
[0,1,0,1],
[0,0,-1,-1]
]).T
u = Matrix([[2,1,4,1]]).T
system = M, u
linsolve(system, x, y, z)
出力:
{(1, 1, 0)}
有限体の線形方程式
sympyでは単純にlinsolveを用いることでは有限体の線形方程式を解くことは出来ません。
以下の$F_2$の線形方程式を考えてみます。
\left(
\begin{array}{ll}
1 & 0 \\
1 & 1 \\
0 & 1
\end{array}
\right)
\left(
\begin{array}{l}
x \\
y
\end{array}
\right)=\left(
\begin{array}{l}
1 \\
0 \\
1
\end{array}
\right)
これは$F_2$では$(x,y)=(1,1)$が解ですが、単純にsympyのlinsolveを使うと、$\mathbb{R}$上で解こうとするので解は存在しないと出力されます。
x,y = symbols('x y')
M = Matrix([
[1,1,0],
[0,1,1]
]).T
u = Matrix([1,0,1]).T
system = M, u
linsolve(system, x, y)
出力:
EmptySet()
しかし、少し工夫することで有限体での線形方程式を解くこともできます。
参考: https://stackoverflow.com/questions/31190182/sympy-solving-matrices-in-a-finite-field
線形方程式を解くためには基本変形を用いて、階段行列にすることで解くことができます。
実際、sympyのlinsolveのドキュメントを見ると、
The algorithm used here is Gauss-Jordan elimination, which results, after elimination, in a row echelon form matrix.
https://docs.sympy.org/latest/modules/solvers/solveset.html?highlight=linsolve#sympy.solvers.solveset.linsolve
とあるように、ガウスの消去法、すなわち行基本変形(row echelon form matrix)を行い、解を求めています。
linsolveでそのまま解を求められないのであれば、有限体の行基本変形を行い、以下のように解くことが出来ます。
from sympy import mod_inverse
from typing import List
from pprint import pprint
DEBUG = True
def mod(x, modulus):
numer, denom = x.as_numer_denom()
return numer*mod_inverse(denom,modulus) % modulus
def linsolve_2gf(M: List[list], u: list):
vecs = M + [u]
aug = Matrix(vecs).T # 拡大係数行列
row, col = aug[:, :-1].shape
# 拡大係数行列を有限体で行基本変形
mat_rref, pivots = aug.rref(iszerofunc=lambda x: x % 2 == 0)
mat_rref = mat_rref.applyfunc(lambda x: mod(x, 2))
if DEBUG:
pprint(mat_rref)
pprint(pivots)
# 得られた階段行列から解を求める。
piv_coeff = mat_rref[:, -1]
root = Matrix.zeros(col, 1) # 解
for i, p_i in enumerate(pivots):
if p_i >= col: continue
root[p_i, 0] = piv_coeff[i]
return root
linsolve_2gf(
[
[1,1,0],
[0,1,1]
],
[1,0,1]
)
出力:
Matrix([
[1, 0, 1],
[0, 1, 1],
[0, 0, 0]])
(0, 1)
Matrix([
[1],
[1]])
何をしているか説明すると、
\left(
\begin{array}{ll}
1 & 0 \\
1 & 1 \\
0 & 1
\end{array}
\right)
\left(
\begin{array}{l}
x \\
y
\end{array}
\right)=\left(
\begin{array}{l}
1 \\
0 \\
1
\end{array}
\right)
を解くために、係数行列と右辺のベクトルをconcatした拡大係数行列
\left(
\begin{array}{ll}
1 & 0 & 1\\
1 & 1 & 0\\
0 & 1 & 1
\end{array}
\right)
を基本変形します。そのコードが以下の部分です。
mat_rref, pivots = aug.rref(iszerofunc=lambda x: x % 2 == 0)
mat_rref = mat_rref.applyfunc(lambda x: mod(x, 2))
1行目は、2で割って0になる場合を0と見なすように行基本変形します。
1行目で得られた結果は、2の倍数をそのまま表示しているので、2行目で行列のそれぞれの成分を2で割った余りとして、有限体上での係数行列を求めています。
結果として、以下の階段行列を得ることができました。
\left(
\begin{array}{ll}
1 & 0 & 1\\
0 & 1 & 1\\
0 & 0 & 0
\end{array}
\right)
この階段行列の右側に解の情報が含まれており、解は拡大係数行列$\tilde{A}\tilde{x}=o$から
\begin{align}
x+0\cdot y = 1 \\
0\cdot x+y = 1 \\
0 = 0
\end{align}
つまり、$x=1, y=1$となっております。
有限体の線形方程式を使ったグラフ理論への応用例
文部科学省が出している行列の教材では、数学活用の例として、グラフ理論に行列を用いて場合の数を求める例があります。(p42,p43 「2.3 行列の場合の数への応用」)
この節では有限体の行列とグラフ理論の関わりを見ていきます。
以下のグラフを考えます。
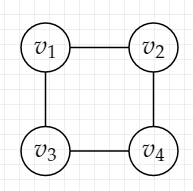
このグラフを有限体の接続行列で表現すると、
\left(
\begin{array}{llll}
1 & 1 & 0 & 0\\
1 & 0 & 1 & 0\\
0 & 1 & 0 & 1\\
0 & 0 & 1 & 1
\end{array}
\right)
接続行列は行に辺、列に点を置いて、辺と点の関係を行列で記述することでグラフを表現する行列の事です。
$$e_1 = \{v_1,v_2\},e_2 = \{v_1,v_3\}, e_3 = \{v_2,v_4\}, e_4=\{v_3,v_4\}$$
として、行列は以下の表の対応となってます。
| $e_1$ | $e_2$ | $e_3$ | $e_4$ | |
|---|---|---|---|---|
| $v_1$ | 1 | 1 | 0 | 0 |
| $v_2$ | 1 | 0 | 1 | 0 |
| $v_3$ | 0 | 1 | 0 | 1 |
| $v_4$ | 0 | 0 | 1 | 1 |
いま、辺同士のベクトルを足し合わせると、例えば、$e_1+e_3=(1,0,0,1)^T$となり$v_1$から$v_4$への経路となってそうです。
この考えを応用し、有限体における線形方程式を解くことで、経路を求めることが出来ます。
例えば、$v_1$から$v_4$への経路を求めたい場合、以下の連立方程式を解くことを考えると、求めることが出来ます。
\left(
\begin{array}{llll}
1 & 1 & 0 & 0\\
1 & 0 & 1 & 0\\
0 & 1 & 0 & 1\\
0 & 0 & 1 & 1
\end{array}
\right)
\left(
\begin{array}{l}
x \\
y \\
z \\
w \\
\end{array}
\right)
=\left(
\begin{array}{l}
1 \\
0 \\
0 \\
1 \\
\end{array}
\right)
この方程式を解いて求められた解$x,y,z,w$は$\{v_1,v_4\}=(1,0,0,1)^T$の辺を求めるために、辺$e_1,e_2,e_3,e_4$を使ったか否かの情報が入ってます。(使った場合は1,使ってない場合は0)
実際、sympyを使って、有限体の連立方程式を解いてみます。
linsolve_2gf(
[
[1,1,0,0],
[1,0,1,0],
[0,1,0,1],
[0,0,1,1]
],
[1,0,0,1]
)
出力:
linsolve_2gf(
[
[1,1,0,0],
[1,0,1,0],
[0,1,0,1],
[0,0,1,1]
],
[1,0,0,1]
)
Matrix([
[1, 0, 0, 1, 1],
[0, 1, 0, 1, 0],
[0, 0, 1, 1, 1],
[0, 0, 0, 0, 0]])
(0, 1, 2)
Matrix([
[1],
[0],
[1],
[0]])
拡大係数行列を基本変形した結果、以下の行列が得られました。
\left(
\begin{array}{lllll}
1 & 0 & 0 & 1 & 1\\
0 & 1 & 0 & 1 & 0\\
0 & 0 & 1 & 1 & 1\\
0 & 0 & 0 & 0 & 0
\end{array}
\right)
これは以下の方程式を満たします。
\begin{align}
x+w = 1 \\
y+w = 0 \\
z+w = 1
\end{align}
今、$w=0$とすると、$x,y,z,w=(1,0,1,0)$が得られ、$v_1$から$v_4$へたどり着くためには$e_1=\{v_1,v_2\},e_3=\{v_2,v_4\}$を経由すれば良いことが求まります。(実装した関数ではパラメーターを0として解を求めてます)
一方で、$w=1$とすると、
\begin{align}
x+1 = 1 \\
y+1 = 0 \\
z+1 = 1
\end{align}
\iff
\begin{array}{l}
x = 0 \\
y = 1 \\
z = 0
\end{array}
となり、$(x,y,z,w)=(0,1,0,1)$が得られ、$e_2=\{v_1,v_3\},e_4=\{v_3,v_4\}$を経由しても$v_1$から$v_4$に辿り着けることが示されました。
まとめ
まとめです。この記事では、以下のことを記述しました。
- sympyはpythonで数式処理を行うライブラリ
- 厳密に計算してくれるので純粋数学の計算のお供に役に立つ!
- sympyを使って代数方程式の解や式展開、因数分解といったことを行うことができる。
- さらに線形代数といった大学で学ぶ代数学の厳密な計算にも応用できる。
本記事では、高校数学~大学数学の初歩程度に言及しましたが、sympyのライブラリでは微分・積分、微分幾何、グレブナー基底、圏論(???)様々な数学モジュールが実装されてます。
数式処理を使ってより良い数学ライフを送りましょう! ^o^
明日は @s_nakamura さんです!