はじめに
最近競プロ熱が再燃して精進している、いおと言います。
AtCoder緑色で、まだまだデータ構造やアルゴリズムを勉強中の身です。
典型90問で出会った「フェニック木」というデータ構造が美しすぎて感動したため、記事にすることにしました。
この美しさが少しでも伝わればと思います。
フェニック木とは
フェニック木 または Binary Indexed Tree (BIT) とは、部分和の計算と要素の更新の両方を効率的に行える木構造である。1994年に算術符号化を用いた圧縮アルゴリズムの計算を効率化するためにピーター・フェニックにより提案された木構造である
(WikiPediaより引用)
簡単にいうと、ある配列に対して部分和を効率的に求められる(計算量でいうとO(log n))上に、値の更新も効率的に行える木構造になります。
サイズNの配列で実現できる上に、実装がとっても簡単なのが魅力的!
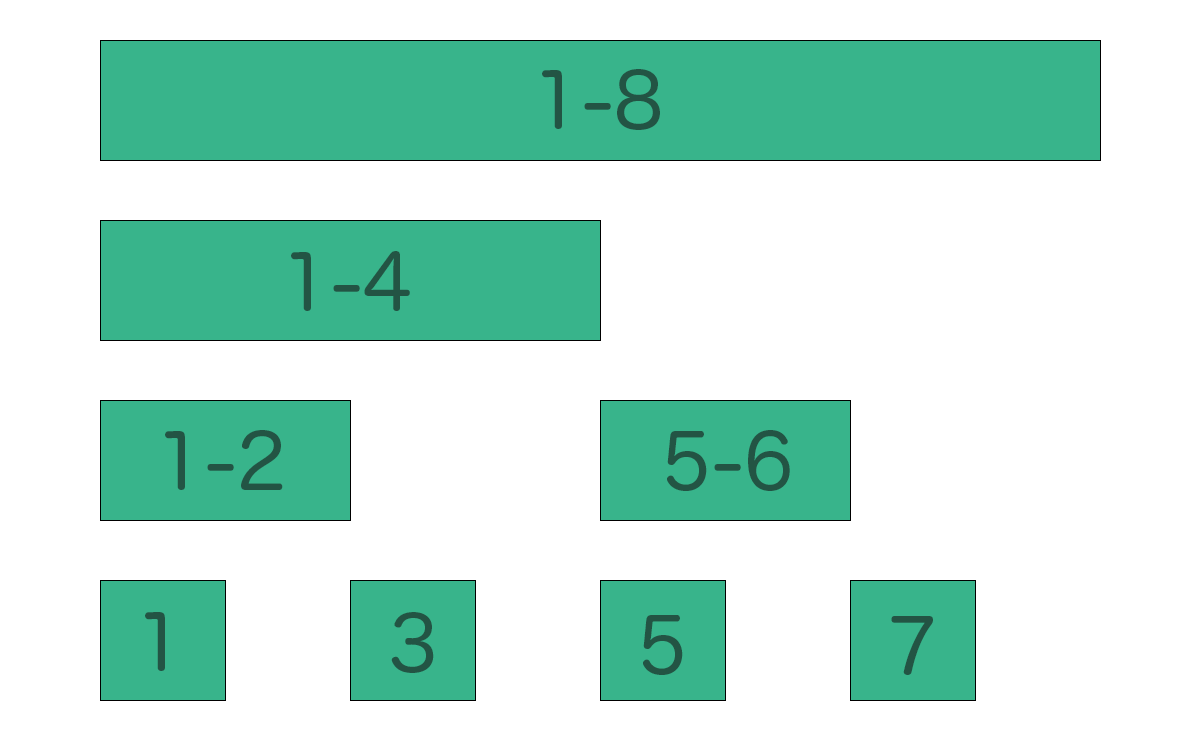
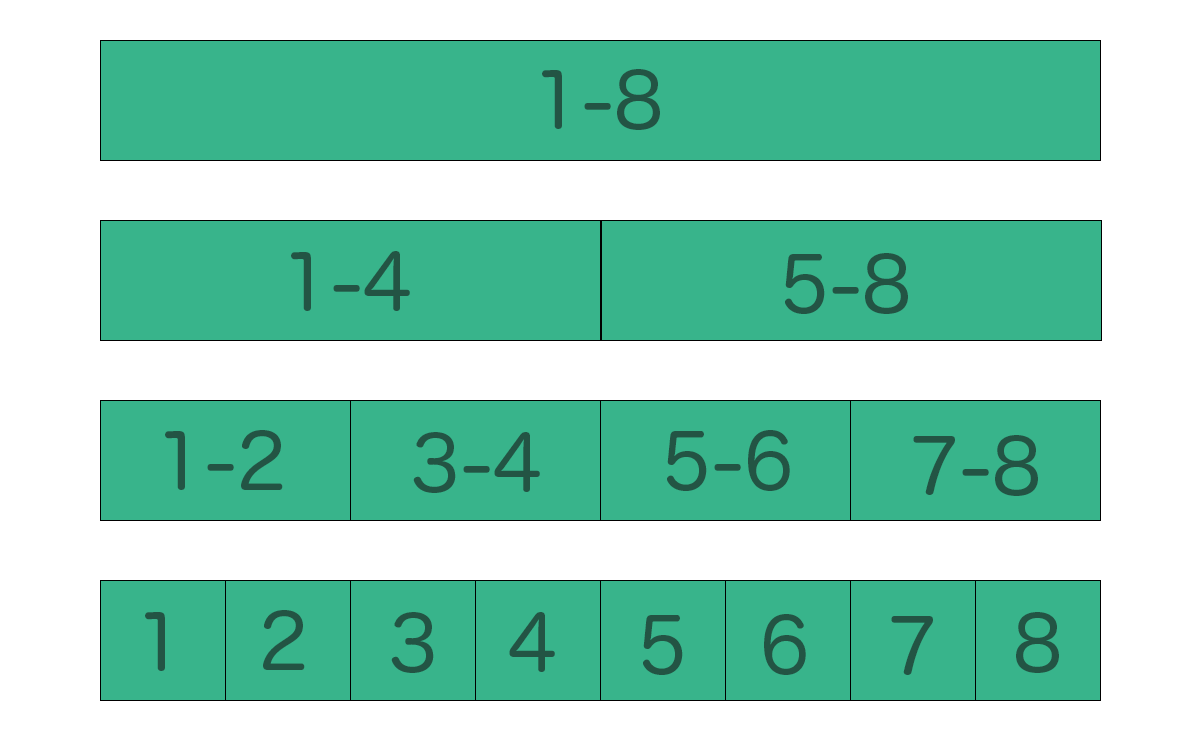
例えば、A[1,2,3,4,5,6,7,8]という等差数列をBIT(今後この配列をこのように呼びます)で表現してみましょう。
BITの各インデックスには下記のように値が格納されています。
# Aの 1番目の値
BIT[1]=1
# Aの 1,2番目の和
BIT[2]=1+2
# Aの 3番目の数
BIT[3]=3
# Aの 1,2,3,4番目の和
BIT[4]=1+2+3+4
# Aの 5番目の数
BIT[5]=5
# Aの 5,6番目の和
BIT[6]=5+6
# Aの 7番目の和
BIT[7]=7
# Aの 1,2,3,4,5,6,7,8番目の和
BIT[8]=1+2+3+4+5+6+7+8
使い方の都合上、BIT[0]は0とします
インデックスは1からです
どういうところがすごいのか?
- 部分和を求める計算に普通は計算量がO(n)かかるところをO(log n)に高速化できる
- クラスで実装しても15行程度と簡単に実装できる
- 元の配列と同じ長さ(N)の配列のみで完結するため、メモリ空間も節約できる
他のデータ構造との比較
部分和の計算と更新に関しては、平衡二分探索木やセグメント木でも実装が可能です。
そもそもフェニック木自体がセグメント木の軽量版です。
しかし、上記の2つは計算量が増えたり、そもそもオーバースペックなところがあります。
平衡二分探索木(詳しくはこちらから)
- 実装が重い
- 計算量が増えてしまう
セグメント木(詳しくはこちらから)
- より汎用性の高いデータ構造で、使い道が多い
- 計算量は数倍になる
- 実装が少し重い
表題の使い方しかしないのであればフェニック木がお得
和の計算の仕組み
例えば、A[1,2,3,4,5,6,7,8]という等差数列の3番目から7番目までの部分和を求めてみようと思います。
これは1~7番目までの和から1~2番目までの和を引くことで求められます。
1~7番目までの和を求めてみましょう
まず、7を2進数で表すと、111(2)となります。
ここで、一番右にある1の桁を0にする操作を順にしていきます。
111(2)→110(2)→100(2)→000(2)
これを10進数に直すと、7→6→4→0となります。
ここで出てきた数をインデックスとして、足し合わせることで和を求めることができます。
sum7=BIT[7]+BIT[6]+BIT[4]+BIT[0] // 28
# BIT[7]=7
# BIT[6]=5+6
# BIT[4]=1+2+3+4
# BIT[0]=0
1~7番目までの和は28です。
同様にして、1~2番目の和は3になります。
010(2)→000(2)より
sum2=BIT[2]+BIT[0] // 3
3番目から7番目までの部分和は
28-3=25
\frac{(7+3)\times(7-3+1)}{2}=25
となり、きちんと計算できたことがわかりました。
値の更新の仕組み
A[1,2,3,4,5,6,7,8]という等差数列の5番目に6を足すと、A[1,2,3,4,11,6,7,8]になります。
こういった値の更新をやってみましょう。
まず、5を2進数で表すと、101(2)となります。
ここで、一番右にある1の桁に1を足す操作を順にしていきます。
N=8を超える前に操作をやめます。
101(2)→110(2)→1000(2)
これを10進数に直すと、5→6→8となります。
ここで出てきた数をインデックスとして、6を足していくことで値を更新することができます。
BIT[5]+=6
BIT[6]+=6
BIT[8]+=6
# BIT[5]=11
# BIT[6]=17
# BIT[8]=44
1~7番目までの和をもう一度求めてみましょう。
sum5=BIT[7]+BIT[6]+BIT[4]+BIT[0] // 34
# BIT[7]=7
# BIT[6]=17
# BIT[4]=10
# BIT[0]=0
1~7番目までの和は34となり、先ほど求めた値に6を足した答えになっています。
実装方法
pythonで実装すると下記のようになります。
class BIT:
# 長さN+1の配列を初期化
def __init__(self, N):
self.size = N
self.bit = [0]*(N+1)
# i番目までの和を求める
def sum(self, i):
res = 0
while i > 0:
res += self.bit[i] # フェニック木のi番目の値を加算
i -= -i & i # 最も右にある1の桁を0にする
return res
# i番目の値にxを足して更新する
def add(self, i, x):
while i <= self.size:
self.bit[i] += x # フェニック木のi番目にxを足して更新
i += -i & i # 最も右にある1の桁に1を足す
各行での操作は、先ほど手動で計算した内容と一緒です。
気になるのは、和の計算と値の更新の両方で登場する-i&iという演算かと思います。
この演算の意味を詳しく考えてみましょう。
bit負数とAND演算の意味
i=7の場合を考えてみましょう。
2進数で7を表すと、111(2)となります。
この時、負数は-i=-7です。
bitで負数を表すときは、2の補数(解説)を用います。
処理としては、bit反転して1を足せば負数になります。
i+(-i)=0
\\
7+(-7)=0
\\
0111(2)+1001(2)=10000(2)(=0000(2))
この0111(2)と1001(2)のAND演算をすると、最も右にある1の桁だけ抽出ができます。
0111(2) \& 1001(2) = 0001(2)
使い方
長さN=10のB[2,6,3,16,7,10,6,3,9,11]という数列に対して、Q=1000回クエリが与えられ、L Rという入力に対してL番目からR番目までの和を出力するという処理をやってみましょう。
N=10 # int(input())
B=[2,6,3,16,7,10,6,3,9,11] # list(map(int, input().split()))
Q=1000 # int(input())
bit=BIT(N)
for i, b in enumerate(B):
bit.add(i+1,b)
for _ in range(Q):
L, R=map(int, input().split())
ans=bit.sum(R)-bit.sum(L-1)
print(ans)
i番目に加算する処理の時に1-indexにすることは忘れないようにしたいですね。
終わりに
ということで、フェニック木(Binary Indexed Tree)の解説でした。
データ構造の解説はしたことがなかったのですが、書いてみることで理解が深まった気がします。
Qiita Engineer Festa 2022という絶好の機会をいただけて良かったです。
処理の仕方や表現に間違っているところがあればご教示お願いいたします。
このシンプルで美しいデータ構造を使いこなせるよう精進していこうと思います。