いろんなソートアルゴリズムを実装してみよう

最近昼夜逆転がひどい六角レンチです
夕方まで起きてようと思ったらいつの間にか寝て夜に起きる謎

haskellに興味を持って入門の記事を見ながらソートを実装して楽しんでます。
ガードとかパターンマッチ楽しい

他にはどんなソートがあるんだろうと思いwikipediaを見ていろいろなソートアルゴリズムを発見したので、pythonの練習として実装してみたいと思います。

実装してみたソートたちはここに置いてます。

バブルソート

def bubblesort(target:list):
    # バブルソート
    for targetrange in reversed(range(1, len(target))):
        isnotswap = True
        for r in range(targetrange-1):
            if target[r] > target[r+1]:
                target[r], target[r+1] = target[r+1], target[r]
                isnotswap = False
        if isnotswap:
            break
    return target

https://ja.wikipedia.org/wiki/バブルソート
バブルソートはリストから一番でかい物をどんどん右に押しやっていく感じのソート方法。

平均計算量が大きい(n^2)ので効率的ではないらしい
実装は一番かんたんだった

どんな感じに動くのか

ソートの動きがわかりやすくなるようにprintを付けた

def bubblesort(target:list):
    # バブルソート
    for targetrange in reversed(range(1, len(target))):
        isnotswap = True
        for r in range(targetrange-1):
            if target[r] > target[r+1]:
                target[r], target[r+1] = target[r+1], target[r]
                isnotswap = False
            print(" ".join(map(str, target)))
            print("  "*(r) + "^ ^")
        if isnotswap:
            break
    return target

ソートするリストを[3, 1, 2, 1, 6, 0, 3, 9, 8]とすると、
まず左端から右端へと最大の数字を持っていく

1 3 2 1 6 0 3 9 8
^ ^
1 2 3 1 6 0 3 9 8
  ^ ^
1 2 1 3 6 0 3 9 8
    ^ ^
1 2 1 3 6 0 3 9 8
      ^ ^
1 2 1 3 0 6 3 9 8
        ^ ^
1 2 1 3 0 3 6 9 8
          ^ ^
1 2 1 3 0 3 6 9 8
            ^ ^
1 2 1 3 0 3 6 8 9
              ^ ^

二つの^における値を比較していき、もし左の値が右の値より大きければ交換する。
これを繰り返していく。

これでリストの中で最大の9を右端に移動できた
つまり、右端を見る必要はもうないので見る範囲を狭める(reversed(range(1, len(target))、このリストだと9から8へ。)
これを繰り返していくことでソートできる。

シェーカーソート

def shakersort(target:list):
    # シェーカーソート
    midnum = int(len(target)/2)
    for i in range(midnum):
        isnotswap = True
        for r in range(i, len(target)-i-1):
            if target[r] > target[r+1]:
                target[r], target[r+1] = target[r+1], target[r]
                isnotswap = False
        for r in reversed(range(i+1, len(target)-i)):
            if target[r] < target[r-1]:
                target[r], target[r-1] = target[r-1], target[r]
                isnotswap = False
        if isnotswap:
            break
    return target

https://ja.wikipedia.org/wiki/シェーカーソート
バブルソートの改良版らしい

バブルソートを前後に、交互に行っていく。
つまり一番大きいやつを右に、一番小さいやつを左にどんどん持っていく

ちなみに平均計算量はバブルソートとあまり変わらないらしい(えぇぇ...)

どんな感じに動くのか

def shakersort(target:list):
    # シェーカーソート
    midnum = int(len(target)/2)
    for i in range(midnum):
        isnotswap = True
        for r in range(i, len(target)-i-1):
            if target[r] > target[r+1]:
                target[r], target[r+1] = target[r+1], target[r]
                isnotswap = False
        for r in reversed(range(i+1, len(target)-i)):
            if target[r] < target[r-1]:
                target[r], target[r-1] = target[r-1], target[r]
                isnotswap = False
        print(" ".join(map(str, target[:i+1])), "|", " ".join(map(str, target[i+1:-i-1])), "|", " ".join(map(str, target[-i-1:])))
        if isnotswap:
            break
    return target

動きがわかりやすくなるようにprintをつけた
ソートするリストを[2, 4, 2, 8, 6, 0, 9, 4, 0, 7]にすると出力は下のようになる

0 | 2 2 4 6 0 8 4 7 | 9
0 0 | 2 2 4 4 6 7 | 8 9
0 0 2 | 2 4 4 6 | 7 8 9

|で囲まれている部分がソートする部分で外の部分はソート済みの部分
端の方から決まっていくのがおもしろいところかな？

バブルソートを双方向にしまくる関係上途中でソートができていることが多い

奇偶転置ソート

def oddevensort(target:list):
    # 奇偶転置ソート
    isnotswap = False
    while not isnotswap:
        isnotswap = True
        for i in range(0, len(target)-1, 2):
            if target[i] > target[i+1]:
                target[i], target[i+1] = target[i+1], target[i]
                isnotswap = False
        for i in range(1, len(target)-1, 2):
            if target[i] > target[i+1]:
                target[i], target[i+1] = target[i+1], target[i]
                isnotswap = False
    return target

https://ja.wikipedia.org/wiki/奇偶転置ソート
シェーカーソートと同じくバブルソートの改良
名前かっこいい

その名の通り奇数の組で比較、置き換えした後偶数の組でも比較、置き換えをしていく感じ

特徴としてそれぞれの比較は独立している
なので、並列処理や並行処理を使ってはやくできる(ただpythonは並列処理遅いんだよね...)

ただし平均計算量はバブルソートやシェーカーソートと同じくn^2で遅い

どう動くのかはwikipediaの動作例見るのがわかりやすい
要は組を分けて交互に比較、交換するを繰り返してるだけ

コムソート

def combsort(target:list):
    # コムソート
    h = int(len(target)/1.3)
    if h < 1:
        h = 1
    while True:
        i = 0
        swap = False
        while i + h < len(target):
            if target[i] > target[i+h]:
                target[i], target[i+h] = target[i+h], target[i]
                swap = True
            i += 1
        if h == 1 and not swap:
            break
        h = int(h/1.3)
        if h < 1:
            h = 1
    return target

https://ja.wikipedia.org/wiki/コムソート
シェーカーソート等と同じくバブルソートの改良版とのこと
なんとシェーカーソート等と違い計算量が(ほぼ)nlognらしい

間隔を付けてどんどん狭めながらバブルソートしていく感じ

どんな感じに動くのか

def combsort(target:list):
    # コムソート
    h = int(len(target)/1.3)
    if h < 1:
        h = 1
    while True:
        print(h, target)
        i = 0
        swap = False
        while i + h < len(target):
            if target[i] > target[i+h]:
                target[i], target[i+h] = target[i+h], target[i]
                swap = True
            print(" ".join(map(str, target)))
            print("  "*i + "^ " + "  "*(h-1) + "^")
            i += 1
        if h == 1 and not swap:
            break
        h = int(h/1.3)
        if h < 1:
            h = 1
    return target

printで可視化してみた
ソートするリストを[6, 0, 1, 3, 7, 1, 7, 4, 7]とすると、

まずリストの長さ/1.3を切り捨てて間隔にする。
このリストの場合9/1.3=6.92...なので切り捨てて6

その後間隔をあけながらバブルソートのように比較、交換していく。

6 [6, 0, 1, 3, 7, 1, 7, 4, 7]
6 0 1 3 7 1 7 4 7
^           ^
6 0 1 3 7 1 7 4 7
  ^           ^
6 0 1 3 7 1 7 4 7
    ^           ^

ソートしたら間隔をまた1.3で割って切り捨てた値を新たな間隔として繰り返していく...
もし間隔が1になって、さらに交換が一度も行われなければソート完了。という感じ

当然ながら間隔は1未満になってはいけないので1未満になったら1とする。

なぜ1.3で割っていく？と思ったので調べたら下の記事を見つけた
https://qiita.com/MKX/items/510a82b2f4cb2290be30

どうやら間隔を小さくしていく速さ(割る時の大きさ)が1.3くらいの時が良いからっぽい

ノームソート

def gnomesort(target:list):
    # ノームソート
    index = 0
    while index != len(target)-1:
        if index == -1:
            index += 1
        elif target[index] <= target[index+1]:
            index += 1
        else:
            target[index], target[index + 1] = target[index + 1], target[index]
            index -= 1
    return target

https://ja.wikipedia.org/wiki/ノームソート
ノーム(とがった三角帽子が特徴的な小さいおじさん。)が植木鉢を整列させていくような動きをするからノームソートというらしい

速さ的には挿入ソートくらいらしい

どうやって動く？

仕組みとしてはすごく単純で、ノームが前に後ろに行ったり来たりするように動く

もしノームが後端(-1)に来たら、なにもないので前に進む。(index += 1)
もしノームが今いる場所にある鉢植えとその前にある鉢植え(target[index]とtarget[index+1])を見て

• 前にある鉢植えが今いる場所の鉢植えより大きかったら、そのまま前に進む。(index += 1)
• 前にある鉢植えが今いる場所の鉢植えより小さかったら、今いる場所にある鉢植えと交換して後ろに下がる。(target[index], target[index + 1] = target[index + 1], target[index]とindex -= 1)

もしノームが前端(len(target)-1)に来たら、ソート完了。


これだけでソートできるの面白い

printを付けてわかりやすくなるようにしてみる

def gnomesort(target:list):
    # ノームソート
    index = 0
    while index != len(target)-1:
        print("  "+" ".join(map(str, target)))
        print(("  "*(index+1))+"^ ^")
        if index == -1:
            index += 1
        elif target[index] <= target[index+1]:
            index += 1
        else:
            target[index], target[index + 1] = target[index + 1], target[index]
            index -= 1
    return target

ソートするリストを[3, 4, 0]とすると、出力は下のようになる

  3 4 0
  ^ ^
  3 4 0
    ^ ^
  3 0 4
  ^ ^
  0 3 4
^ ^
  0 3 4
  ^ ^
  0 3 4
    ^ ^

^はノームが確認している鉢植え(数字)
行ったり来たりしているのが面白い

選択ソート

def selectionsort(target:list):
    # 選択ソート
    for i in range(len(target)):
        min_index = i
        for index in range(i+1, len(target)):
            if target[min_index] > target[index]:
                min_index = index
        target[i], target[min_index] = target[min_index], target[i]
    return target

https://ja.wikipedia.org/wiki/選択ソート
最小の物をどんどん探していく感じのソート方法

当然遅い。

どんな感じに動くのか

def selectionsort(target:list):
    # 選択ソート
    for i in range(len(target)):
        print(target[:i], "|", target[i:])
        min_index = i
        print(" ".join(map(str, target[i:])))
        print("^ "+ "  "*(len(target)-i), target[min_index])
        for index in range(i+1, len(target)):
            print(" ".join(map(str, target[i:])))
            print("  "*(index-i) +"^ " + "  "*(len(target)-index), target[min_index], ">", target[index], target[min_index] > target[index])
            if target[min_index] > target[index]:
                min_index = index
        target[i], target[min_index] = target[min_index], target[i]
    return target

可視化するためにprintを付けた
ソートするリストを[4, 2, 5]とすると、出力は下のようになる

[] | [4, 2, 5]
4 2 5
^        4
4 2 5
  ^      4 > 2 True
4 2 5
    ^    2 > 5 False
[2] | [4, 5]
4 5
^      4
4 5
  ^    4 > 5 False
[2, 4] | [5]
5
^    5
[2, 4, 5]

対象から最小の値を探して、返すリストに移動させる。これを繰り返す
ただそれだけなのでバブルソートより簡単かもしれない

挿入ソート

def insertsort(target:list):
    # 挿入ソート
    for i in range(1, len(target)):
        val = target[i]
        changeindex = 0
        for r in reversed(range(i)):
            changeindex = r
            if val >= target[r]:
                changeindex += 1
                break
        target[changeindex+1:i+1] = target[changeindex:i]
        target[changeindex] = val
    return target

https://ja.wikipedia.org/wiki/挿入ソート
その名の通り挿入していくソート方法

バブルソートと何が違う？って最初思ったけどあちらはどんどん右に移動させていくのに対してこっちは新しくリストを作ってその場所に入れていくような感じ
(これ見てわかった。動きがわかりやすい)

どんな感じに動くの？

def insertsort(target:list):
    # 挿入ソート
    for i in range(1, len(target)):
        print(target[:i], "|", target[i:])
        val = target[i]
        changeindex = 0
        for r in reversed(range(i)):
            changeindex = r
            print(" ".join(map(str, target[:i])), "")
            print(("  "*r) + "^" + "  "*(i-r), val, ">=", target[r], val >= target[r])
            if val >= target[r]:
                changeindex += 1
                break
        target[changeindex+1:i+1] = target[changeindex:i]
        target[changeindex] = val
    print(target)
    return target

動きがわかりやすくなるようにちょっと改造した
ソートするリストを[9, 5, 8, 5, 2, 4, 1, 3, 9, 2]にする。
出力の中でも5回目のループの出力を見てみると

[0, 1, 3, 7, 9] | [5, 4, 3, 6, 2]
0 1 3 7 9
        ^   5 >= 9 False
0 1 3 7 9
      ^     5 >= 7 False
0 1 3 7 9
    ^       5 >= 3 True
[0, 1, 3, 5, 7, 9] | [4, 3, 6, 2]

最初に表示される二つのリストの内、前が挿入先のリスト。後ろは挿入元のリスト(ソートするリスト)
^の値と挿入元のリストの左端の値を比較していき、

• もし^の値が挿入元のリストの左端の値以下であればその左の場所に挿入
• 最後まで比較して挿入先のリストになければ、左端に追加

という感じでどんどん挿入していく。

chatgptに改善してもらったばーじょん

def insertsort_optimized(target: list): 
    for i in range(1, len(target)):
        key = target[i]
        left = 0
        right = i - 1
        while left <= right:
            mid = (left + right) // 2
            if target[mid] < key:
                left = mid + 1
            else:
                right = mid - 1
        target[left+1:i+1] = target[left:i]
        target[left] = key
    return target

chatgptに改善してくださいって要求したら帰ってきたコード

なんと二分探索を入れてきた

いや二分探索ってまじか...と感じた
(というのも、挿入先のリストは必然的にソート済みになるので二分探索できる。ということに気づけなかった)

ボゴソート

def bogosort(target:list):
    # ボゴソート
    import random
    while True:
        random.shuffle(target)
        for i in range(len(target)-1):
            if target[i] > target[i+1]:
                break
        else:
            break
    return target

https://ja.wikipedia.org/wiki/ボゴソート
みんな大好き(？)ボゴソート

ランダムにシャッフルして値がちゃんと連続してたらソート完了

実用性なんてあるわけない

平均計算量は(値が揃ってるか確認するところの計算量を考えないで)n×n!らしい
...階乗!?

ストゥージソート

def stoogesort(target:list):
    # ストゥージソート
    if target[0] > target[-1]:
        target[0], target[-1] = target[-1], target[0]
    if (listrange := len(target)) >= 3:
        kirutoko = int((listrange-1)*(2/3)) + (1 if str((listrange-1)*(2/3)).split(".")[1] != 0 else 0) # 切り上げ
        target[:kirutoko] = stoogesort(target[:kirutoko])
        target[-kirutoko:] = stoogesort(target[-kirutoko:])
        target[:kirutoko] = stoogesort(target[:kirutoko])
    return target

https://ja.wikipedia.org/wiki/ストゥージソート
一風変わったソート

二つしかif文ないしなんか再帰使ってるし速そう！！！

しかし計算量はn^(log3/log1.5)≒n^2.7くらいととんでもなく遅い
(バブルソートの計算量はn^2)

そして知名度が無いせいか解説が全くないのでなんでこれでソートできるのか自分では理解できなかった
本当になんでこれだけでソートできるんだこれ...

アルゴリズムはwikipedia見てください(解説無理)

ちなみに名前は三ばか大将(The Three Stooges)というコメディー？が元ネタの模様

マージソート

def mergesort(target:list):
    # マージソート
    def merge(rlist:list, llist:list) -> list:
        returnlist = []
        rindex = 0
        lindex = 0
        while rindex != len(rlist) and lindex != len(llist):
            if rlist[rindex] >= llist[lindex]:
                returnlist.append(llist[lindex])
                lindex += 1
            else:
                returnlist.append(rlist[rindex])
                rindex += 1
        returnlist.extend(rlist[rindex:])
        returnlist.extend(llist[lindex:])
        return returnlist

    if len(target) <= 1:
        return target
    else:
        kirutoko = len(target)//2
        return merge(mergesort(target[:kirutoko]), mergesort(target[kirutoko:]))

https://ja.wikipedia.org/wiki/マージソート
コムソートと同じく計算量がnlognのソート方法

同じnlognだけど実はこっちの方がはやい

どんどん分割してそのあとに合成(マージ)していく感じのソート方法

解説無理(再帰の説明難しい)なので適当に検索してください
(解説してるサイトたくさんある)

クイックソート

def quicksort(target:list):
    # クイックソート
    if len(target) <= 1:
        return target
    else:
        pipot = target[len(target)//2]
        rindex = len(target)-1
        lindex = 0
        while True:
            while not target[rindex] <= pipot:
                rindex -= 1
            while not target[lindex] >= pipot:
                lindex += 1
            if rindex > lindex:
                if target[rindex] != target[lindex]:
                    target[rindex], target[lindex] = target[lindex], target[rindex]
                rindex -= 1
                lindex += 1
            else:
                break
        return quicksort(target[:lindex]) + quicksort(target[lindex:])

https://ja.wikipedia.org/wiki/クイックソート
とんでもない早さを誇るソートアルゴリズムです

平均計算量はコムソートやマージソートと同じくnlognですが、これらより体感1.5倍くらい早いです
但し最悪計算量がn^2なので一長一短

仕組みは難しいのですが、なんか値をとって（ピポット）、その値以上の値しかないリストとそれ未満の値しかないリストを再帰的に作っていく感じです

気を付けたいのが、参考にしたwikipediaでは

配列の先頭（左側）から順に、値が P 以上の要素を探索してその位置 LO を記憶する
配列の終端（右側）から逆順に、値が P 未満の要素を探索してその位置 HI を記憶する

とあるのですが、このHIを記憶するとき未満ではなく以下じゃないといけないので注意(間違っている)

例えば。[1, 2, 1, 3, 3]というリストで中央にいる1をピポットとして選び、wikipediaの通りにやると

• 右から見始めてピポット未満の要素が無いのでHI=-1
• 左から見始めて1を0で見つけてLO=0
• HI<=LOなのでLOで分割(スライス)
• リスト[:0]とリスト[0:]をまたクイックソート

という感じになり、無限ループになってしまいます。

未満ではなく以下にすると

• 右から見始めて1を2で見つけてHI=2
• 左から見始めて1を0で見つけてLO=0
• どちらも1なので交換しない(別にしても大丈夫だけど計算の無駄)
• 続きから見て1を0で見つけてHI=0
• 続きから見て2を1で見つけてLO=1
• HI<=LOなのでLOで分割(スライス)
• リスト[:1]とリスト[1:]をまたクイックソート

クイックソートを続ける...

といった感じで無限ループじゃなくなります。

ちなみにピポットの選択はこの実装のように真ん中を選ぶのではなく、乱数で選んだ場所や中央値の場所を選んだ方が良いらしいのですが、乱数使ったら遅くなったのでそのままにしています。

速度比較

ボゴソートとストゥージソートの速度測定はしません。
ボゴソートはまぁ測れる限度が低すぎますし、ストゥージソートは遅すぎます。

いっぱいソートの実装をしたので、ソートの速度を比較してみます。
クイックソートの実装時間かかったから速いと嬉しいな

timeitで時間を測ったあと、matplotlibでグラフを書く。
(実はmatplotlib使うの初めてだったりする)

環境

• CPU Core i7 4770
• OS Windows10
• Python 3.9.6 64-bit

CPUが古いって？
言ってはいけない。

ソートするリスト

ソート対象のリストは下の関数使って作る

def random_list_gen(num:int, maxnum:int = 9) -> list:
    import random
    return [random.randint(0, maxnum) for _ in range(num)]

引数として、要素数と要素の最大値を受け取り、ランダムに作っていく感じ。
値が重複する可能性がある。(その方が現実っぽいかなぁっていう理由)

要素数はどんどん変化させて、最大値は固定で10000000(1000万)にする。

計測

まずは要素数100~1000まで50ずつ増加させて見てみる
サンプル数は1000

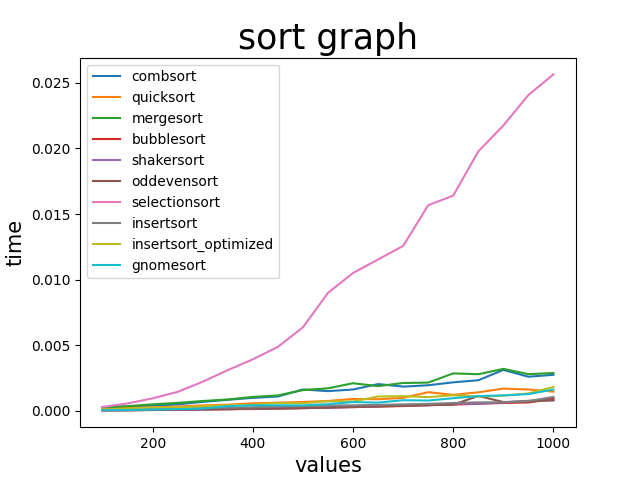
縦軸は一回のソートにかかった時間。横軸はソートしたリストの要素の数。
下に行くほど速い(つまり効率が良い)ソートになる。
逆に、上へ行くほど遅い(効率が悪い)ソートになる。

明らかに遅すぎる奴がいる。選択ソート君...
まぁそうなるだろうなとは思ったけどここまでとは

これじゃ他のソートがよくわからないので選択ソート君を抜いてもう一度計測してみる

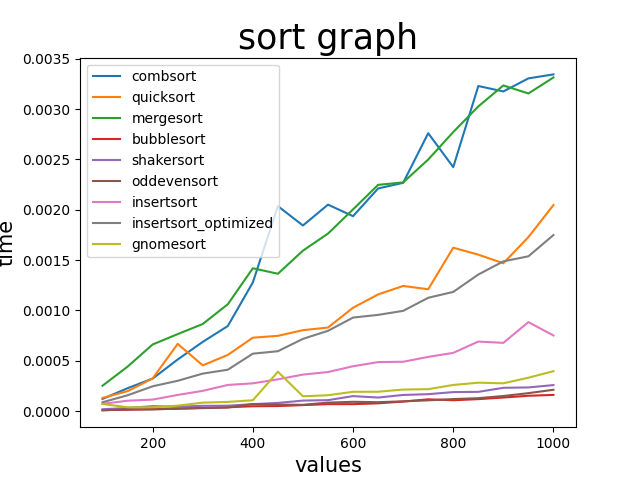
面白いことに、nlognの速さを持つはずのコムソート、マージソートがこの量だと逆に遅い。(あれ？実装間違えたかな...)

逆に早いのはバブルソート、奇偶転置ソート、シェーカーソート、ノームソートといった面々。
遅いと聞いていたので逆に早くてびっくり

ただこの時間だともはや誤差レベルな気がするが

AIが書いた方の挿入ソートがクイックソートと同じ速さなのは面白い。
AIが書いた方の挿入ソートは二分探索を使ってるのでそこがネックになってそう

次は5000個まで500ずつ増加させてみる。
サンプル数は減らして300

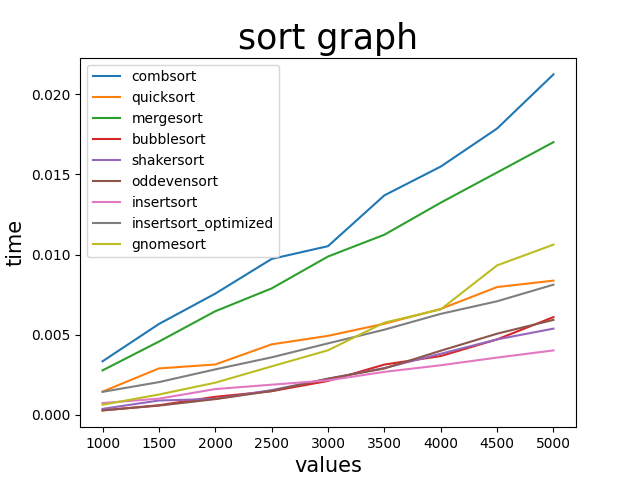
...なんも変わってる気がしない。

しいて言うならノームソートの時間の伸び方が急な感じくらいか

というかコムソートとマージソートはいつまで上にいるんだこれ
5000個って結構多い気がしたんだけどなぁ

ということで10000個まで500ずつ増加させてみる
サンプル数は少し下げて200

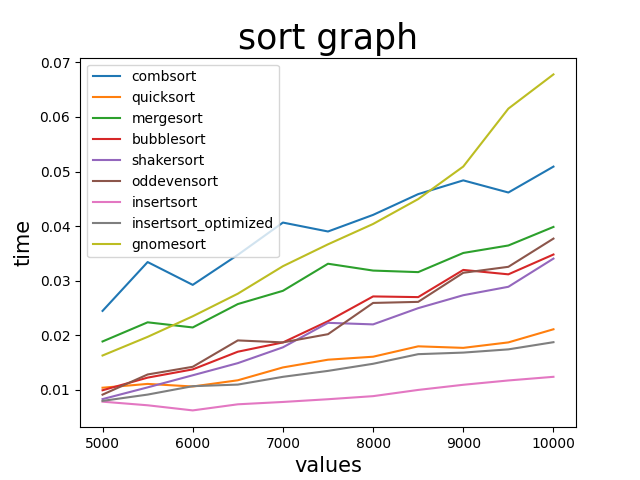
ようやく変化が訪れた

まずノームソートがかなり遅くなっている。
(コムソート君最下位脱却)

さらに、よく見てみるとバブルソートやシェーカーソート、奇偶転置ソートも遅くなってマージソートと同じくらいの位置になっている

その影響によりこの範囲で早いソートは挿入ソート、AIが書いた方の挿入ソート、クイックソートの順。

ノームソートはこのまま増加していきそうなのでここで抜いておこうかな
(コムソート君また最下位のお知らせ)

次は20000まで2000ずつ増加させてみよう。
サンプル数は100

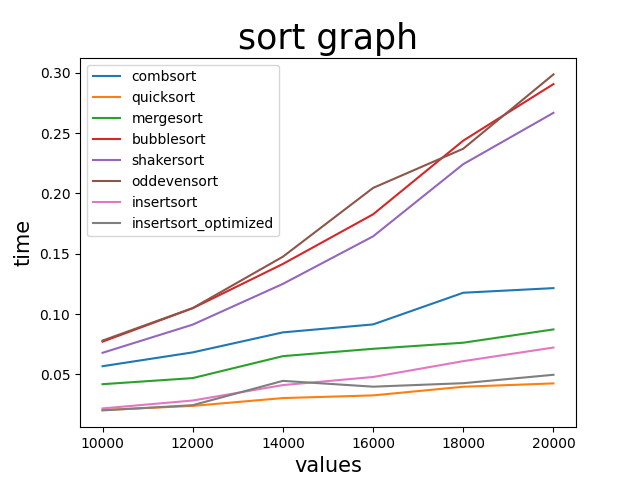
なんと挿入ソート以外のオーダーn^2のやつ(バブルソート、奇偶転置ソート、シェーカーソート)がすごい遅くなっている
流石にここまでくると無理があるか

そしてオーダーN^2の割になぜここまで挿入ソートが速いのか疑問が生じる
コムソートやマージソートより速く、なんなら12000以下ならクイックソートレベルの速さを持っている
(コムソート、マージソートの実装が下手な可能性ある)

再帰が遅いのかな？いやでもコムソートは再帰使ってないしな...

とりあえずバブルソート、奇偶転置ソート、シェーカーソートはどんどん増加していくと考えられそうなので、ここで抜いておく。

残りはコムソート、マージソート、挿入ソート、AIが書いた方の挿入ソート、そしてクイックソートといった感じ

次は50000まで5000ずつ行ってみよう。
サンプル数は50

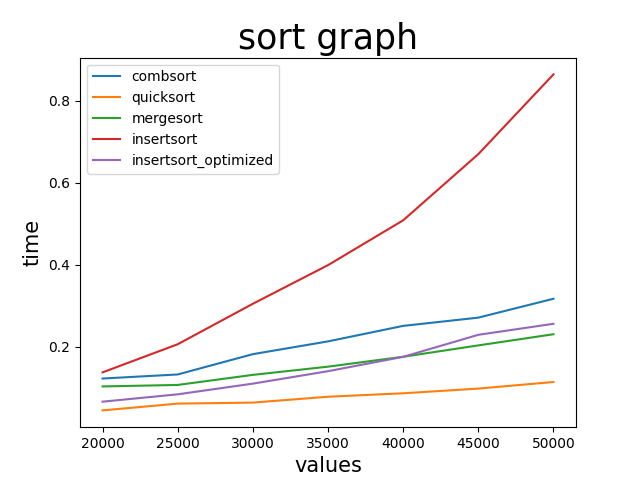
ようやく普通の挿入ソートが遅くなった。
にしても挿入ソートってこんなに早いのか？

そして特筆すべきなのはAIが書いた方の挿入ソート、すなわち二分探索を採用した挿入ソートがいまだに生き残っているということ。

いくらなんでも強すぎないか...
さすがに40000辺りからマージソートに負けてはいるものの、よく考えたら挿入ソートはオーダーN^2のはずなのでとんでもなく早いことになる(他は全部オーダーNlogN)

最後に、100,000まで10000ずつ増加させてみる。
サンプル数は25

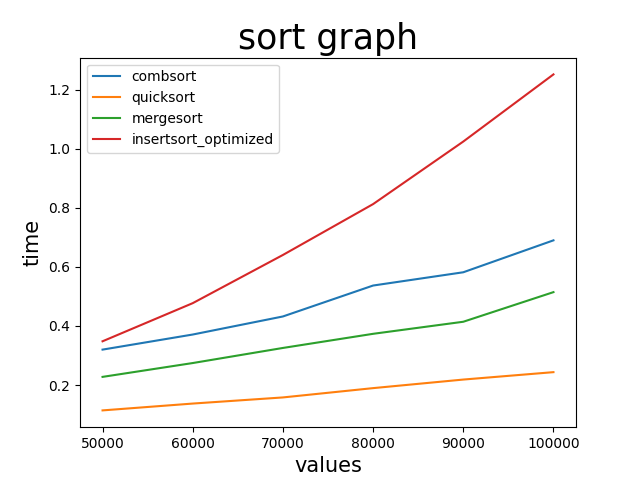
ようやく遅くなった感じ

これが二分探索(オーダーlogN)の力なのか...

再現したい人向け

ソースを置いている場所にこの検証で使用したソースファイルを置いておきました。
(speedtest.py)

もし再現したかったらこのファイルの下にあるプロファイルを変えて実行してみてください
新しいプロファイルを作って計測してみるのも結構楽しいですよ

おわり

実際に実装してみると色々なソート方法ありますね

そして検証してみると同じ計算量でも違いがあるのもおもしろい

そういえばNlogNのソート同士の順位は最初から変わらず、上からコムソート、マージソート、クイックソートという順番でしたね

N^2の方はノームソートが早々に遅くなったり最初は他と比べて遅かった挿入ソートが最後まで生き残っていたり

...選択ソート？誰のことですか？
まぁ全探索するのでそりゃそうなるわって感じですけど

気になる事として、なぜ挿入ソートがあそこまで速いのでしょうか？
途中クイックソートレベルの速さを出していましたし、二分探索を採用した方は計算量の割にかなり耐えていましたし...

ソート対象のリストの生成関数が良くなかったのか？
それとも他のソートの実装が遅いのか？
謎です。

自分的に好きなのはノームソートです
動きが面白い

参考にしたもの

• ほぼwikipedia読んで作りました
• クイックソートのアルゴリズムの説明間違えてたの許さない

• バブルソートと挿入ソートの違いが全くもってわからなかったけどこれ見てわかった

おまけ

色々なソートを実装したのでやりたいことができました。
それは...

ボゴソートで要素数1000のリストソートしたい

しかしそのままでは1000*1000!というとんでもない計算量になってしまう...(絶望)

どうすればいいんだ？

ということでボゴ・マージソート作ります。

マージソートの仕組みは検索してほしいのですが、マージソートのマージの部分で要求するのはソート済みのリストです。
(実際にこれを応用したのがpythonの標準ソートになってるティムソート)

つまり、程よく分割した後にボゴソートでソートしたものをマージすれば、実質ボゴソートです。
（ほんまか）

ちなみにクイックソートも似たような感じなのでやろうと思えばボゴ・クイックソートも作れます

ただし、クイックソートの性質上ピポットの選択によってはもはやボゴソートいる？ってなるような要素数(2個だけとか)に分割される可能性があるので、2等分する関係上常に要素数が一定になるマージソートを選びました。

ボゴソートで現実的な計算量なのは8個くらい。(平均計算量はx*x!なので8x8!=322560)
1000を128で割ると大体8になるので128回くらいボゴソートでソートした後マージすると考えると10**8くらいの計算量でソートできそう(多分)

ということで作りました。

コード

def bogo_mergesort(target:list):
    # ボゴ・マージソート
    def _bogosort(target:list):
        # ボゴソート
        import random
        while True:
            random.shuffle(target)
            for i in range(len(target)-1):
                if target[i] > target[i+1]:
                    break
            else:
                break
        return target

    def _merge(rlist:list, llist:list) -> list:
        returnlist = []
        rindex = 0
        lindex = 0
        while rindex != len(rlist) and lindex != len(llist):
            if rlist[rindex] >= llist[lindex]:
                returnlist.append(llist[lindex])
                lindex += 1
            else:
                returnlist.append(rlist[rindex])
                rindex += 1
        returnlist.extend(rlist[rindex:])
        returnlist.extend(llist[lindex:])
        return returnlist

    if len(target) <= 8:
        return _bogosort(target)
    else:
        kirutoko = len(target)//2
        return _merge(bogo_mergesort(target[:kirutoko]), bogo_mergesort(target[kirutoko:]))

ランダムな数字生成器

また、ランダムな要素を作るために、下の関数を用意した。

def random_list_gen(num:int, maxnum:int = 9) -> list:
    import random
    return [random.randint(0, maxnum) for _ in range(num)]

値が重複する可能性ある。(それも込み)
今回は最大値を10000にして使う

環境

• OS : Windows10
• CPU : Core i7 4770
• Python : 3.9.6 64-bit

試運転

試運転として百個の要素をソートしてみる
timeitを使います

下のコードで計測します
(sortsはモジュール名なので気にしないでください。)

timeit("sorts.bogo_mergesort(a)", "a=sorts.random_list_gen(100, 10000)", number=100, globals=globals())/100 

0から10000までのランダムな数字を100個入れたリストのソートする時間を100回測り、平均をとる感じです。

実行結果

0.07650497499999971

0.07秒か...まぁいけるだろ

本番

下のコードで計測します

timeit("sorts.bogo_mergesort(a)", "a=sorts.random_list_gen(1000, 10000)", number=100, globals=globals())/100 

sorts.random_list_gen(100, 10000)がsorts.random_list_gen(1000, 10000)になっただけです。

実行結果

15.527962130999999

すごい時間かかった...(15秒*100=1500秒=25分)
母数100は多すぎましたね

ただ平均15秒でソートできました
ボゴソートの計算量考えるとすごいはやーい

...おまけが本編になってませんかねこれ？