Uiuaとは?
Uiua (wee-wuh) is a general purpose, stack-based, array-oriented programming language with a focus on simplicity, beauty, and tacit code.
公式サイトによると、「Uiuaは簡潔さ、美しさ、及び暗黙的なコードに焦点を当てた、一般的な用途のスタックベース及び配列志向のプログラミング言語」と紹介されています。
特徴的なこととして、組み込み関数のためにglyphを採用しています。
+-×÷を始めとする四則演算や平方根を表す√は馴染み深いものの、
☇や¤といった馴染みのない記号もサポートされています。
公式ドキュメントに組み込み関数の一覧が出ているため、
興味のある方はこちらから進んでいくのも良いかと思います。
このglyphは記号として入力することも、
対応する組み込み関数の名前を記述することによっても利用することが可能です。
例えば、+はaddとして使え、☇はrerank、¤はfixとして使うことが出来ます。
本記事の内容は2023年12月18日時点のものであり、
新しく導入された関数や廃止された関数が存在する可能性があります。
最新情報は公式ドキュメントを参照してください。
環境構築
公式サイトでPlaygroundが用意されているため、
気になった方はとりあえず公式サイトで遊んでみるのが良いかと思います。
また後述するマルチメディア出力に関しては公式サイトで遊んだ方が楽なため、
個人的にはやらなくても良い工程かと思いますが記載しておきます。
ローカルに環境構築を行う場合、OSがWindowsかどうかで大きく変わります。
Windowsを使っている場合は公式レポジトリのlatest releaseからダウンロードすることが可能です。
他のOSの場合はcargoコマンドを使えるようにした上で次のコマンドでインストール可能です。
ただし、cargoコマンドを使えるようにするには、Rustの環境構築が必要になります。
Rustの公式ドキュメントを参考に環境構築を進めると良いです。
~$ cargo install uiua
ここで次のエラーが出る場合は、Rustのアップデートが必要になります。
~$ cargo install uiua
Updating crates.io index
error: failed to download `uiua v0.3.1`
Caused by:
unable to get packages from source
Caused by:
failed to parse manifest at `(省略)/uiua-0.3.1/Cargo.toml`
Caused by:
feature `edition2021` is required
this Cargo does not support nightly features, but if you
switch to nightly channel you can add
`cargo-features = ["edition2021"]` to enable this feature
Rustのアップデートは次のコマンドで行えます。
~$ rustup update stable
インストール後は作業を行いたいディレクトリでuiua initを叩くことで初期化を行うことができ、uiua runにより実行できます。
~$ uiua init
~$ uiua run
"Hello, World!"
また、Uiua言語の拡張子である.uaファイルが存在する状態でuiuaコマンドを実行することで、.uaファイルに変更が入った場合は、インタープリタが自動的にフォーマットし実行してくれます。
~$ uiua
Watching for changes... (end with ctrl+C, use `uiua help` to see options)
―――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
"Hello, World!"
―――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
"Hello, World?"
watching for changes...
冒頭で述べたように、glyphは対応する組み込み関数の名前を書くことでも利用できますが、折角なのでglyphを使ってコードを書きたいと思うはずです。
しかしglyphを他のアルファベットと同じように簡単に入力できる人は殆どいないと思います。
そこでVSCode向けに提供されている公式の拡張機能を使うと、ファイル保存時に自動的にglyphに変換してくれます。
そのため次のコードは保存されると、
add1 2
equals 3
このようにglyphに変換されて保存してくれます。
+1 2
= 3
書いてみる
何はともあれ書いてみましょう。
Uiuaでは他の多くの言語と異なり「右から左」にコードが実行されます。
これはUiuaがスタックベースの言語であり、スタック指向の言語では無いからです。
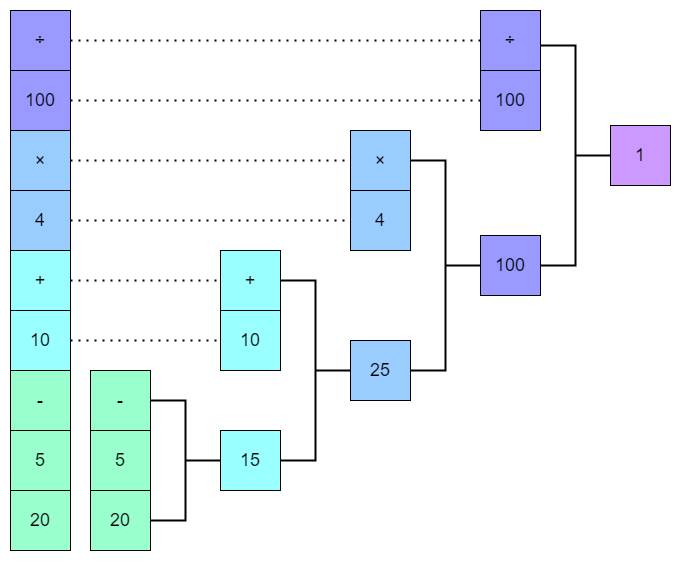
簡単に次の式を計算してみましょう。
( 20 - 5 + 10 ) × 4 ÷ 100
Uiuaでは次のように書くことができます。
÷ 100 × 4 + 10 - 5 20
----
1
計算されるイメージとしては次のような感じですかね。
このように記述しても正しく計算されます。
÷ × + - 5 20 10 4 100
----
1
この場合だと次のような感じで計算されますね。
マルチメディア出力
Uiuaでは画像やGIF、音楽すら作ることが出来ます。
今回は試しに音を出してみようと思います。
基本
ここの内容は公式ドキュメント自分なりに噛み砕いたものであるため、
手っ取り早く読みたい方は公式ドキュメントを読むことをおススメします。
Uiuaには&asrと呼ばれる音声出力のための、サンプルレートを定数化したものがあります。
&asrには44100が登録されており、一般的なCDで使われるサンプリング周波数の値が入っています。
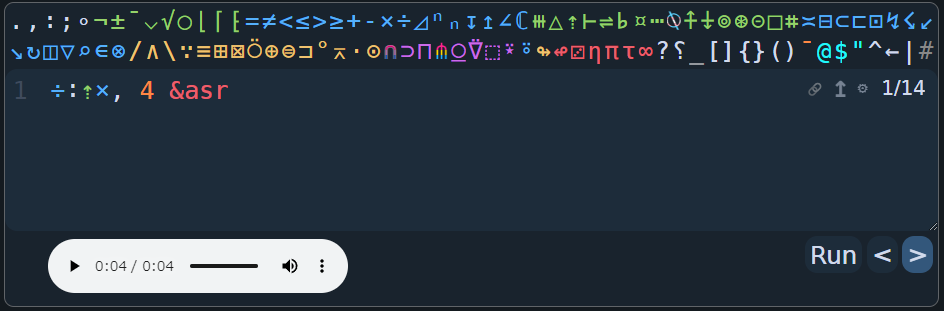
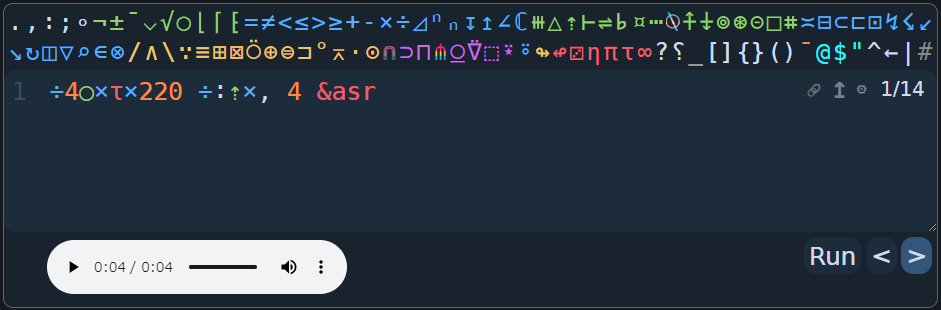
これだけでは音声出力は出来ないですが、次のようにすると4秒間の音声出力が可能になります。
÷:⇡×, 4 &asr
順番に見ていくと、
-
&asrにより44100をスタックに乗せる - 4を44100の上に乗せる
-
,はoverを表し、スタックのうち上から2番目の値をコピーする
つまり、&asrである44100をコピーする -
×により4と44100を乗算し、176400を作る -
⇡はrangeを表し、対象の数字未満の自然数からなる配列を作る
つまり、[0 1 ... 176398 176399]を作る -
:はflipを表し、スタック上の上から2つの値を交換する -
÷により配列全体を44100で除算する
画像にすると次のような感じですね。
これによりサンプリングレート(44100Hz)に対し、要素数が4倍の配列が完成するため、これだけで4秒間の音声出力が可能になります。
とはいえ配列の中身が0から約4までの単調増加の値であるため音として認識できません。
そこで次は音を出せるようにしていきます。
÷:⇡×, 4 &asr
この結果は先に見たように、0から約4までの値が単調増加で176400個入っています。
これを音の情報に変換するには、幾つかの手法があります。
物理基礎で学んだ方が多いと思いますが、波形と音色には関係があることが分かっています。
特にシンセサイザーを触ったことがある人には馴染み深いと思いますが、以下のものが有名ですね。
- 正弦波
- 三角波
- 矩形波
- ノコギリ波
ここでは分かりやすさのために正弦波を扱ってみます。
正弦波は次のように表されますね。(簡単のために初期位相は0とします)
y = Amp \sin(2\pi*freq*time)
つまり先ほど手に入れた配列の要素を、この関数の値に変換すれば正弦波が出力されるはずです。
また先の工程により、配列の要素には約4秒の時間をサンプリングレートで割った値が入っているため、既に時間が入っていることになります。
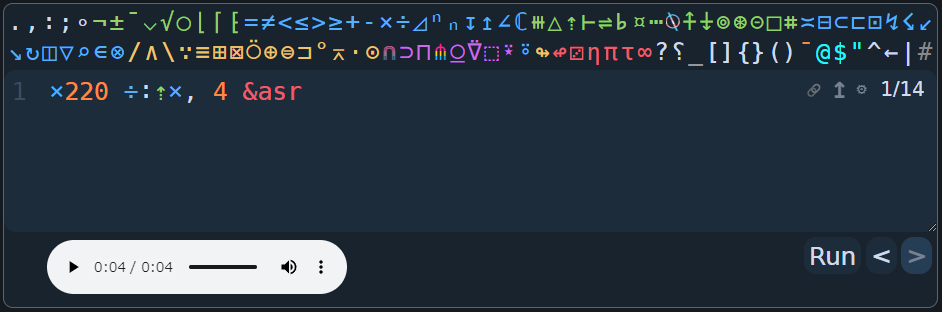
あとは任意の周波数freqに2倍の円周率を掛けて、それぞれの値に対して正弦を取れば完成ですね!
×220 ÷:⇡×, 4 &asr
まず、任意の周波数、ここでは220を掛けてみます。
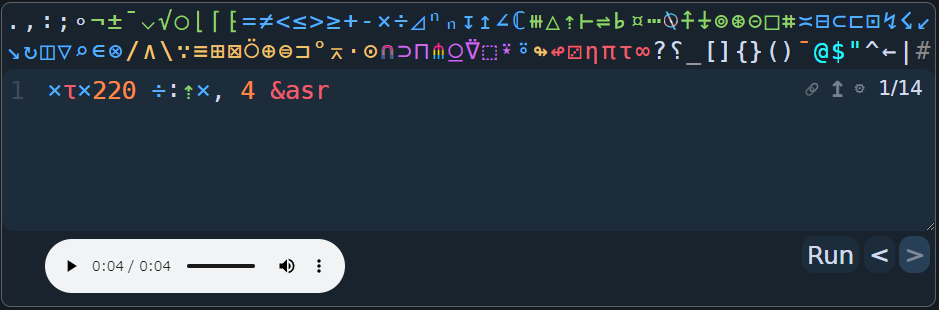
×τ×220 ÷:⇡×, 4 &asr
そして円の半径に対する円周比を表すτ、tauを掛けます。
このτは2πに等しいですね。
○×τ×220 ÷:⇡×, 4 &asr
あとは○を付与します。
これはsineを意味し、これにより値の正弦を取ることが出来ます。
ただし、このまま再生すると音量が大きいため、好みの1より大きい値で割ると耳に優しくて良いですね。
今回は4で割っています。
÷4○×τ×220 ÷:⇡×, 4 &asr
これによって4秒間、220Hzの正弦波が出力されます。
こんなにすっきりした形で音が出せちゃうんです。
今すぐ公式サイトにコピペして再生してみましょう!
くれぐれも音量には注意して再生してください
次は複数の音を鳴らして和音を出してみたくなりますよね?
しかし前提知識として筆者は音階と周波数の関係をよく知りません。
そこで「高校数学の美しい物語」の記事を参考にすると、音階と周波数の近似値が掲載されています。
幾つか記事の内容をピックアップすると以下のことが分かります。
- ある音の1オクターブ上は元の周波数の2倍になる
- 1オクターブの間を等比数列となるように12等分したものが平均律である
- 音の周波数が簡単な整数比で表される場合に心地よいと感じる
以上のことにより、1つ周波数を決めてしまえば、和音を構成する音の周波数が全て分かることになります。
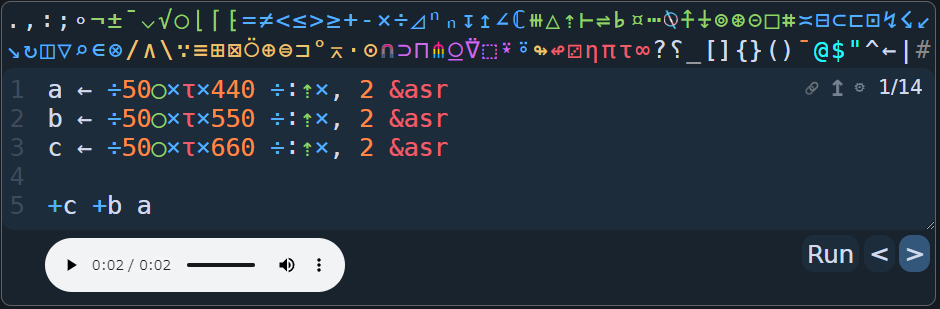
ここでは基底となる周波数を440Hzとすると、550Hzと660Hzの音を同時に奏でれば、和音になりそうだと分かります。
あとは複数の周波数の音を同時に鳴らせば良いので、これで動くはずです。
a ← ÷50○×τ×440 ÷:⇡×, 2 &asr
b ← ÷50○×τ×550 ÷:⇡×, 2 &asr
c ← ÷50○×τ×660 ÷:⇡×, 2 &asr
+c +b a
確かにこれで動作はするのですが、コードの冗長さがUiuaらしくないですね。
先に引用したように、特定の周波数から2倍の周波数までを等比数列となるように12分割すると音階が作れ、それを平均律と呼びます。
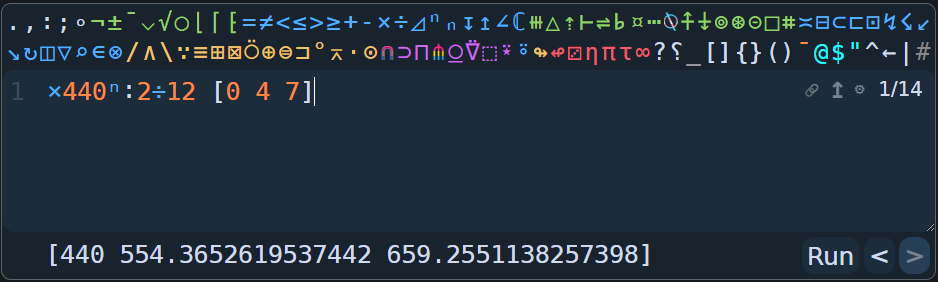
この部分は次のように書くことが出来ますね。
×440ⁿ:2÷12 [0 4 7]
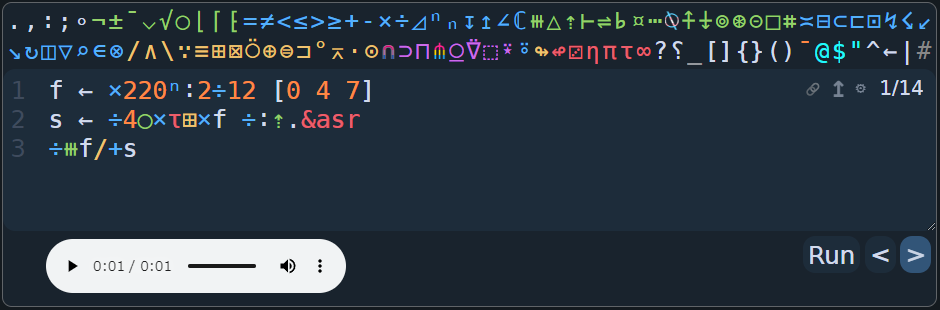
後はこれを変数に入れて、最初に扱った時間の配列と乗算をすれば和音を鳴らせられますね。
ちなみに先の[0 4 7]はそれぞれド ミ ソを表すので、和音になります。
f ← ×220ⁿ:2÷12 [0 4 7]
s ← ÷4○×τ⊞×f ÷:⇡.&asr
÷⧻f/+s
応用
さて、下記のコードをコピペして実行すると、初代ポケモンのマサラタウンのBGMが流れます。
楽譜はこちらの動画から引用させていただきました。
https://www.youtube.com/watch?v=Cs6hLa7HbL4
このような感じで音楽を作って流すことも出来ちゃいます。
ここではMelodyFreqを適当に変えると、調が変わって楽しめますし、
音の音色を定義しているKindをSawからSinに変えると、ノコギリ波から正弦波に変わるため音色が変わって楽しめます。
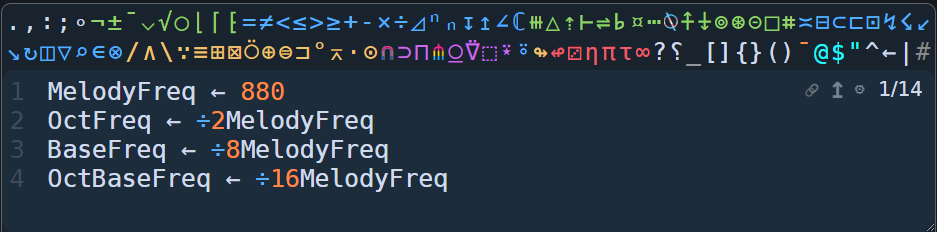
MelodyFreq ← 880
OctFreq ← ÷2MelodyFreq
BaseFreq ← ÷8MelodyFreq
OctBaseFreq ← ÷16MelodyFreq
ss ← 1/16
s ← 1/8
m ← 1/4
l ← 1/2
ml ← 3/4
ll ← 1
llm ← 5/4
Saw ← ÷10◿1⊞×
Sin ← ÷10○×τ⊞×
Kind ← Saw
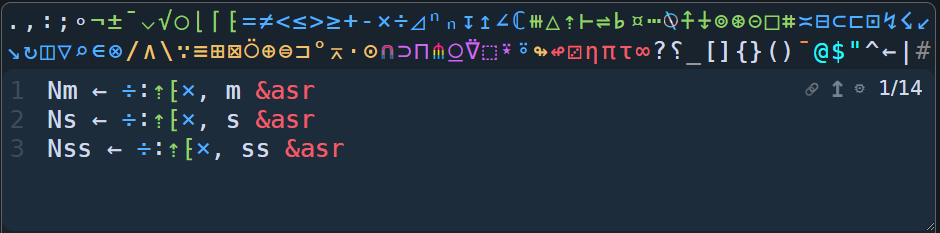
Nm ← ÷:⇡⁅×, m &asr
Ns ← ÷:⇡⁅×, s &asr
Nss ← ÷:⇡⁅×, ss &asr
oE ← ×OctFreqⁿ:2÷12 [4]
oEl ← Kind oE ÷:⇡⁅×,l&asr
oElm ← ÷⧻oE/+oEl
oF ← ×OctFreqⁿ:2÷12 [6]
oFm ← Kind oF ÷:⇡⁅×,m&asr
oFmm ← ÷⧻oF/+oFm
oFml ← Kind oF ÷:⇡⁅×,ml&asr
oFmlm ← ÷⧻oF/+oFml
oG ← ×OctFreqⁿ:2÷12 [7]
oGm ← Kind oG ÷:⇡⁅×,m&asr
oGmm ← ÷⧻oG/+oGm
oGl ← Kind oG ÷:⇡⁅×,l&asr
oGlm ← ÷⧻oG/+oGl
oGll ← Kind oG ÷:⇡⁅×,ll&asr
oGllm ← ÷⧻oG/+oGll
A ← ×OctFreqⁿ:2÷12 [9]
Am ← Kind A ÷:⇡⁅×,m&asr
Amm ← ÷⧻A/+Am
Al ← Kind A ÷:⇡⁅×,l&asr
Alm ← ÷⧻A/+Al
Aml ← Kind A ÷:⇡⁅×,ml&asr
Amlm ← ÷⧻A/+Aml
B ← ×OctFreqⁿ:2÷12 [11]
Bs ← Kind B ÷:⇡⁅×,s&asr
Bsm ← ÷⧻B/+Bs
Bm ← Kind B ÷:⇡⁅×,m&asr
Bmm ← ÷⧻B/+Bm
Bl ← Kind B ÷:⇡⁅×,l&asr
Blm ← ÷⧻B/+Bl
Bml ← Kind B ÷:⇡⁅×,ml&asr
Bmlm ← ÷⧻B/+Bml
Bla ← Kind B ÷:⇡⁅×,ll&asr
Blam ← ÷⧻B/+Bla
Bllm ← Kind B ÷:⇡⁅×,llm&asr
Bllmm ← ÷⧻B/+Bllm
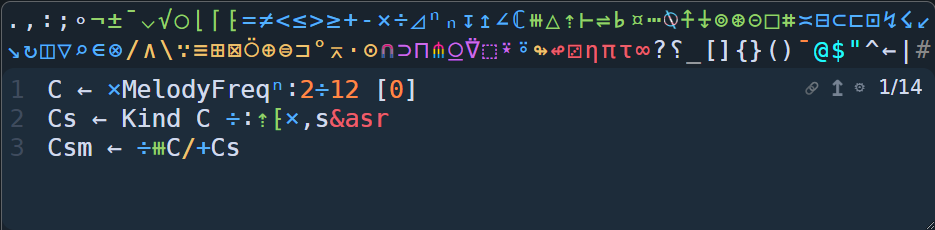
C ← ×MelodyFreqⁿ:2÷12 [0]
Cs ← Kind C ÷:⇡⁅×,s&asr
Csm ← ÷⧻C/+Cs
Cm ← Kind C ÷:⇡⁅×,m&asr
Cmm ← ÷⧻C/+Cm
Cl ← Kind C ÷:⇡⁅×,l&asr
Clm ← ÷⧻C/+Cl
Cml ← Kind C ÷:⇡⁅×,ml&asr
Cmlm ← ÷⧻C/+Cml
Cll ← Kind C ÷:⇡⁅×,ll&asr
Cllm ← ÷⧻C/+Cll
D ← ×MelodyFreqⁿ:2÷12 [2]
Ds ← Kind D ÷:⇡⁅×,s&asr
Dsm ← ÷⧻D/+Ds
Dm ← Kind D ÷:⇡⁅×,m&asr
Dmm ← ÷⧻D/+Dm
Dl ← Kind D ÷:⇡⁅×,l&asr
Dlm ← ÷⧻D/+Dl
Dml ← Kind D ÷:⇡⁅×,ml&asr
Dmlm ← ÷⧻D/+Dml
E ← ×MelodyFreqⁿ:2÷12 [4]
Em ← Kind E ÷:⇡⁅×,m&asr
Emm ← ÷⧻E/+Em
El ← Kind E ÷:⇡⁅×,l&asr
Elm ← ÷⧻E/+El
Eml ← Kind E ÷:⇡⁅×,ml&asr
Emlm ← ÷⧻E/+Eml
F ← ×MelodyFreqⁿ:2÷12 [6] # F#
Fm ← Kind F ÷:⇡⁅×,m&asr
Fmm ← ÷⧻F/+Fm
Fml ← Kind F ÷:⇡⁅×,ml&asr
Fmlm ← ÷⧻F/+Fml
G ← ×MelodyFreqⁿ:2÷12 [7]
Gm ← Kind G ÷:⇡⁅×,m&asr
Gmm ← ÷⧻G/+Gm
lA ← ×OctBaseFreqⁿ:2÷12 [9]
lAl ← Kind lA ÷:⇡⁅×,ll&asr
lAlm ← ÷⧻lA/+lAl
lC ← ×BaseFreqⁿ:2÷12 [0]
lCl ← Kind lC ÷:⇡⁅×,ll&asr
lClm ← ÷⧻lC/+lCl
lD ← ×BaseFreqⁿ:2÷12 [2]
lDl ← Kind lD ÷:⇡⁅×,ll&asr
lDlm ← ÷⧻lD/+lDl
lDml ← Kind lD ÷:⇡⁅×,ml&asr
lDmlm ← ÷⧻lD/+lDml
lE ← ×BaseFreqⁿ:2÷12 [4]
lEl ← Kind lE ÷:⇡⁅×,ll&asr
lElm ← ÷⧻lE/+lEl
lG ← ×BaseFreqⁿ:2÷12 [7]
lGl ← Kind lG ÷:⇡⁅×,ll&asr
lGlm ← ÷⧻lG/+lGl
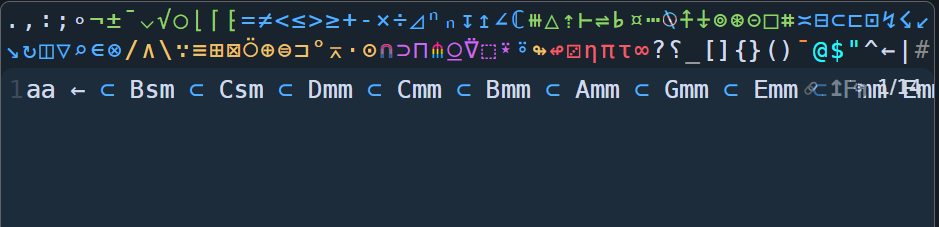
aa ← ⊂ Bsm ⊂ Csm ⊂ Dmm ⊂ Cmm ⊂ Bmm ⊂ Amm ⊂ Gmm ⊂ Emm ⊂ Fmm Emm
ab ← ⊂ Dmlm ⊂ Bmm ⊂ oGmm ⊂ oGmm ⊂ Amm ⊂ Bmm ⊂ Cllm Nm
ac ← ⊂ oFmm ⊂ oGmm ⊂ Amm ⊂ Bmlm ⊂ Csm ⊂ Bsm ⊂ Amlm ⊂ Bsm Csm
melodyFir ← ⊂ aa ⊂ ab ac
ba ← ⊂ Dmm ⊂ Cmm ⊂ Bmm Dmm
bb ← ⊂ Gmm ⊂ Fmm ⊂ Fmm Gmm
bc ← ⊂ Emlm Dmm
bd ← ⊂ Dmlm Nm
be ← ⊂ Cmm ⊂ Bmm ⊂ Amm oGmm
bf ← ⊂ Dmm ⊂ Cmm ⊂ Bmm Amm
bg ← oGllm
melodySec ← ⊂ ba ⊂ bb ⊂ bc ⊂ bd ⊂ be ⊂ bf bg
ca ← ⊂ Nm ⊂ oGmm ⊂ Amm Bmm
cb ← ⊂ Cmlm Nm
cc ← ⊂ Dmlm Cmm
cd ← ⊂ Bllmm ⊂ oGmm ⊂ Amm Bmm
ce ← ⊂ Cmm ⊂ Nm ⊂ Cmm Nm
cf ← ⊂ Dmlm ⊂ Csm Dsm
cg ← Blam
ch ← ⊂ Nm ⊂ Bmm ⊂ Amm oGmm
ci ← ⊂ Amlm Nm
cj ← ⊂ oElm Blm
ck ← ⊂ Amlm Nm
cl ← ⊂ oGlm oElm
cm ← ⊂ oFmlm Nm
cn ← ⊂ oGlm Blm
co ← ⊂ Bmlm Nm
cp ← Amlm
melodyThr ← ⊂ ca ⊂ cb ⊂ cc ⊂ cd ⊂ ce ⊂ cf ⊂ cg ⊂ ch ⊂ ci ⊂ cj ⊂ ck ⊂ cl ⊂ cm ⊂ cn ⊂ co cp
# Adjust like "↘ ¯1"
melody ← ↘ ¯4 ⊂ melodyFir ⊂ melodySec melodyThr
# ÷5 melody
baseFir ← ⊂ Nm ⊂ lGlm ⊂ lClm ⊂ lGlm ⊂ lElm ⊂ lClm ⊂ lDlm ⊂ lGlm lDlm
baseSec ← ⊂ lGlm ⊂ lClm ⊂ lGlm ⊂ lElm ⊂ lClm ⊂ lDlm ⊂ lGlm lElm
baseThr ← ⊂ lClm ⊂ lDlm ⊂ lGlm ⊂ lElm ⊂ lClm lDlm
baseFou ← ⊂ lGlm ⊂ lElm ⊂ lAlm ⊂ lAlm ⊂ lAlm ⊂ lAlm ⊂ lDlm ⊂ lElm ⊂ lClm lDmlm
base ← ⊂ baseFir ⊂ baseSec ⊂ baseThr baseFou
# ÷5 base
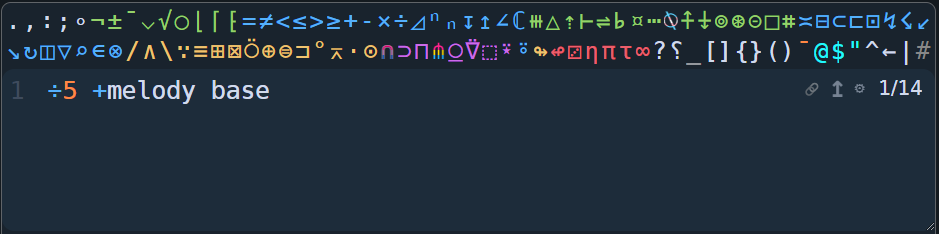
÷5 +melody base
可読性は犠牲になりました。
以下に、簡単に何をしているかを解説しておきます。
ここではCの音の周波数を決めています。
そのためA及びBの音を出す際には1オクターブ下の周波数を元に計算しています。
またベースの音を3オクターブ下にしています。
MelodyFreq ← 880
OctFreq ← ÷2MelodyFreq
BaseFreq ← ÷8MelodyFreq
OctBaseFreq ← ÷16MelodyFreq
音の長さを定義しています。
ss ← 1/16
s ← 1/8
m ← 1/4
l ← 1/2
ml ← 3/4
ll ← 1
llm ← 5/4
ノコギリ波と正弦波の定義をしています。
◿はmodulusを表します。
Saw ← ÷10◿1⊞×
Sin ← ÷10○×τ⊞×
Kind ← Saw
休符の定義をしています。
音を発したくない場所では、必要な長さだけこの値を差し込んでいます。
Nm ← ÷:⇡⁅×, m &asr
Ns ← ÷:⇡⁅×, s &asr
Nss ← ÷:⇡⁅×, ss &asr
その後しばらくは音階の定義が続くので、ここではCの音を例として取り上げます。
先に扱った平均律の式を利用して音の周波数を計算した後、音の長さに合わせて波形を算出しています。
基本の部分では出てこなかったglyphとして、⁅があります。
これはroundを意味し、四捨五入を行ってくれます。
音の長さが短くなる場合、サンプリング周波数との積の結果が自然数にならず、
対象が自然数の必要がある⇡ rangeが使えなくなる可能性があるため、roundを差し込んでいます。
C ← ×MelodyFreqⁿ:2÷12 [0]
Cs ← Kind C ÷:⇡⁅×,s&asr
Csm ← ÷⧻C/+Cs
ここまでで必要な音符は作りきることが出来るため、後は音を繋げていく工程になります。
この操作を連続して行うことでメロディーを構成します。
aa ← ⊂ Bsm ⊂ Csm ⊂ Dmm ⊂ Cmm ⊂ Bmm ⊂ Amm ⊂ Gmm ⊂ Emm ⊂ Fmm Emm
最終的にメロディーの音を構成している配列と、
ベースの音を構成している配列を足し合わせる必要があります。
ここでは配列の要素数を合わせるために、メロディーの最後の数要素を落としています。
短い音を生成する際に四捨五入をしているため、僅かに生じる誤差を修正しています。
# Adjust like "↘ ¯1"
melody ← ↘ ¯4 ⊂ melodyFir ⊂ melodySec melodyThr
最終的にメロディーの配列とベースの配列を足し合わせ、音量を調整したら完成です。
÷5 +melody base
今回は安直に用いる音の種類と長さの組み合わせを全パターン定義しましたが、もっと良い方法があるように思えますね。
特にUiuaの命名規則を完全に逸脱しているので、次に似たようなことをする方がいれば気にして記載して頂けると良いかと思います。
所感
少し書いてみた感想を記載しておきます。
難しい所
-
glyphを使いこなすのに時間を要する
Uiua最大の魅力であるglyphですが、かなり習熟度に大きく左右されると思いました。 -
書いてから時間が空くと全く理解できなくなる
Uiuaだから……という話では無いですが、
可読性の低さが相まって、時間の経過と共に何を書いていたか分かりにくくなりました。
良い所
-
環境構築をしなくても公式サイトで遊ぶことが出来る
新しい言語を始める上で環境構築のハードルはそれなりにあるので、スキップすることが出来るのは大きいメリットですね。 -
マルチメディアの出力が出来る
たった数行のコードで複雑なフラクタルや音声の出力、GIFの作成まで行えるのはとても魅力的ですね。 -
可読性が低いは楽しい
難しい所にも可読性の話は書きましたが、可読性の低さは楽しさに直結しますね。
仕事で書くコードでやられたらたまらないですが。
終わりに
今回は音に着目してUiuaで遊んできましたが、
公式サイトにあるようにGIFや画像を作って遊ぶことも出来ます。
思い思いの楽しみ方を見つけて、Uiuaを盛り上げていきましょう!