はじめに
サッカー好きな人はもちろんのことそうでない人でもほとんどの人が知っているリオネル・メッシ
彼の打ち出したリーガエスパニョーラシーズン最多得点記録(50ゴール)という大記録はどれほどすごいのか、
どれだけの年月が経てば彼ほどの選手が現れるのかを極値統計という手法を用いて推測しました。
極値統計とは？
極値統計学とは、豪雨、強風などの極端な自然現象や、ファイナンスなどでリスク評価のために応用される統計手法です。一般に統計学では母集団の中心に対する推測を行っていますが、極値統計学は、極端な現象、すなわち、母集団分布の端(最大値や最小値)に対する推測を行います。
一般化極値分布
極値を表す確率分布は、Gumbel分布、Frechet分布、Weibull分布の3つのタイプに分類できることが知られています。
これら3つの分布が一般化極値分布（GEV）という、次の1つの式で表現できることがわかっています。
G(z)=exp[-(1+ξ(\frac{z−μ}{σ})^\frac{-1}{ξ})]
パラメーターは3つで、ロケーションを示すμスケールを示すσ形を示すξとなります。今日では上記の式で表せられる一般化極値分布をまず推定し、そこから3つのうちのどれに当たるかを推定するという手法が採られています。具体的には、
ξ=0のときにGumbel分布、ξ>0のときにFrechet分布、ξ<0のときにWeibull分布となります。
得点王データ
今回はWikipediaを参照し、リーガエスパニョーラの1928-29から2017-18シーズンまでの約90年間得点王の得点数をもとに得点王の得点数に関する極値分布を作成する。
得点数のグラフをプロットすると下図のようになります。
date <- read.csv("liga.csv",header =FALSE)
#データのプロット
plot(date[,1], type = "h", xlab = "",
ylab = "Scorers", main = "Top Scorers Liga ")
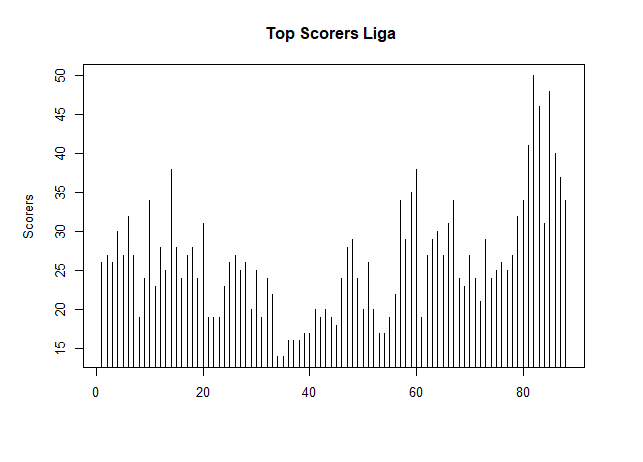図を見てわかる通り近年のメッシとロナウドの得点数がどれほどすごいか一目瞭然でした。（笑）
極値分布のあてはめ
Rの極値理論のライブラリであるismevとextRemesを用いてデータを極値分布に適応します。
library(ismev)
library(extRemes)
fitgev <- fevd(date[,num], type = "GEV")
パラメータ
par.gev <- distill(fitgev)[1:3]
par.gev
#location scale shape
#22.81797313 5.81334547 -0.01777088
推定したパラメータはξ(shape)<0よりWeibull分布に従うことがわかります。
モデルの検証
モデルを検証するために
推定結果のうちメジャーな4つのグラフをプロットします。
par(mfrow=c(2,2))
plot.fevd(fitgev, type = "probprob", main="Probability plot")
plot.fevd(fitgev, type = "qq", main="Quantile plot")
plot.fevd(fitgev, type = "rl", main="Return level plot")
plot.fevd(fitgev, type = "density", main="Density plot")
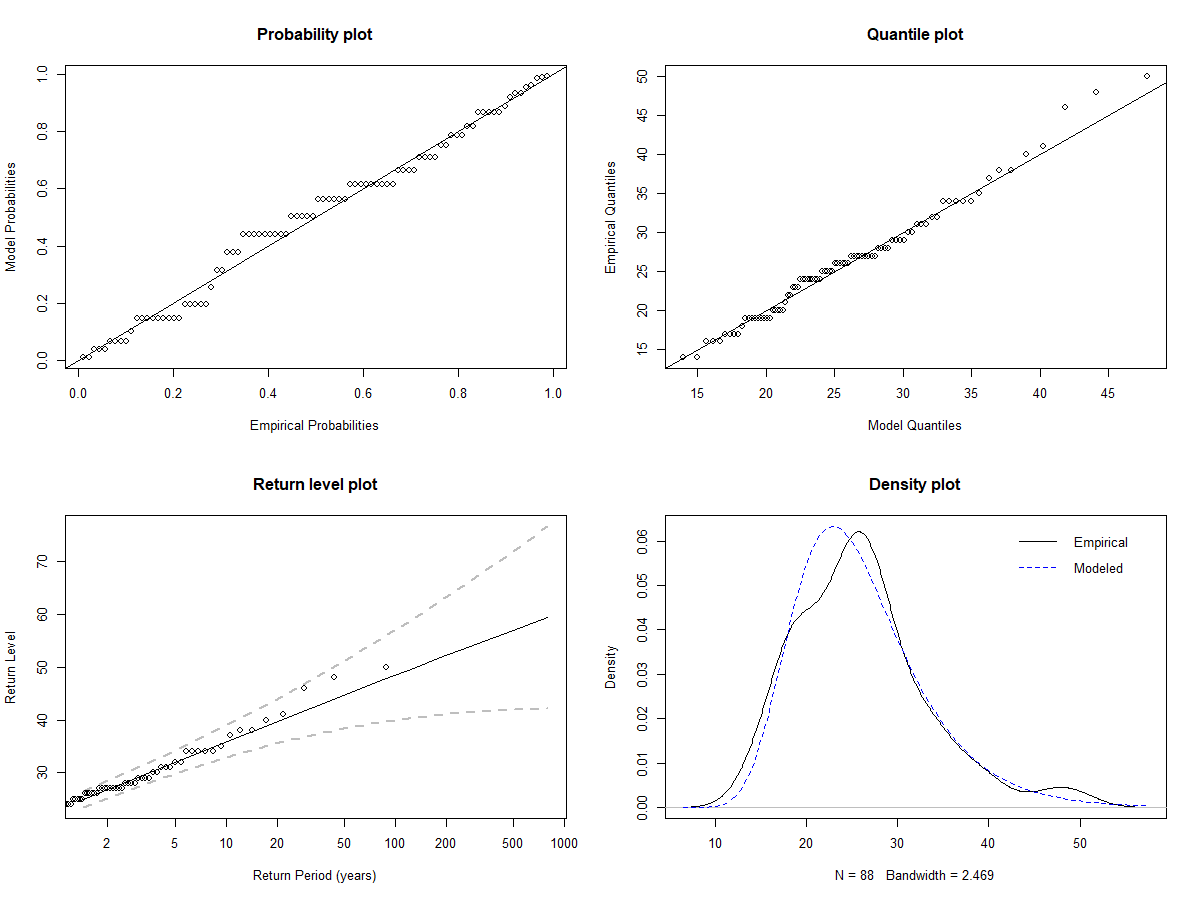左上と右上はそれぞれprobability plot,quantile plotと呼ばれているもので、かなりざっくりした説明をすると対角線に沿っているほど分布のあてはまりが良いといえるものです。
また、Return level plotではそれぞれの値が95％以内には収まっていることを示しています。
最後に、Density Plotはサンプルデータと推定モデルが概ね一致していることがわかります。
結局メッシはどれだけすごいのか
推定したモデルよりメッシの打ち出したシーズン50ゴールが何年に一度のものなのか推定します。
scores <-50
mYears <- 1 / (1 - pevd(scores, loc=par.gev[1], scale=par.gev[2], shape=par.gev[3]))
mYears
結果は・・・
132.3342年！
メッシは132年に一度の天才だということができました！
つまり彼ほどの選手が現れるのにはあと132年の年月が必要ということです。
おまけ
生成したモデルから得点数の再現レベルが分かります。メッシはおよそ100年に一度の天才であることがわかりましたが、1000年に一度の天才はどれだけの得点を重ねるかわかります。
ci.fevd(fitgev, type = "return.level", return.period = 1000)
結果は 60.606点でした！
リーガエスパニョーラは年間38試合なので全試合得点してさらに二試合に一回は二得点しなければいけません
メッシも凄すぎますが、1000年に一度となるともはや凄すぎて訳が分からない次元ですね（笑）