golang
golang complex(複素数)型を使うで基本的な使い方を解説しています。
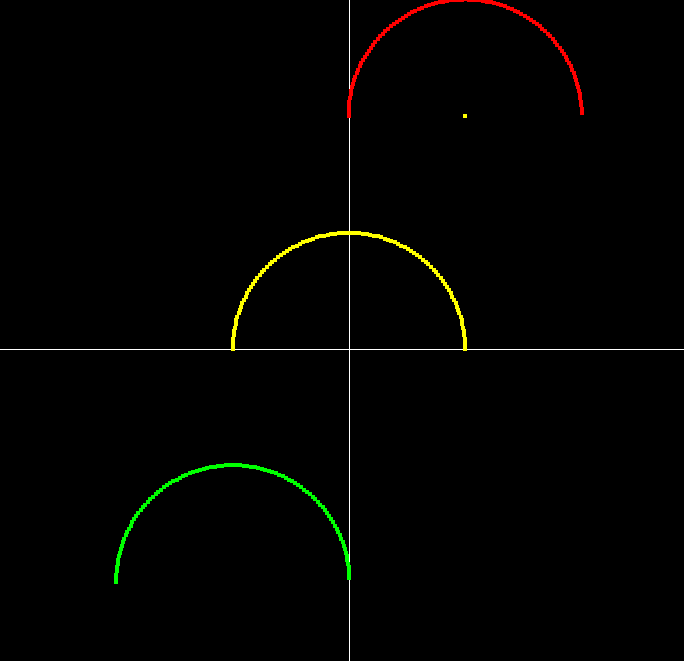
今回はこういう画像を使って解説します。
縦軸=虚数 (上が3i、下が-3i)
横軸=実数 (左が-3、右が3)
絶対値
math/cmplxパッケージのAbs()関数で絶対値を求めることができます。

水色の矢印の長さが絶対値です。
水色の線と、黄色の点から垂直に降りる線と、横軸の線をつなぐと直角三角形で、黄色の点の座標から水色の線(斜辺)の長さを求めることができます。
これはピタゴラスの定理の計算です。
実数型と複素数型で比較してみます。
float64でのピタゴラスの定理の計算
f1 := 1.0
f2 := 2.0
ans := math.Sqrt(math.Pow(f1, 2) + math.Pow(f2, 2))
complex128での絶対値の計算
c := 1+2i
ans := math.Abs(c)
複素数の仕組みさえ分かっていれば、このようにとても短く書くことができます。
加算,減算 -> 座標の移動とベクトルの加算・減算
黄色の円黄色の円は初期値(足される、引かれる前の数)です。
加算すると右上に、左下に来ることがわかります。
加算と減算はそのまま座標がずれる計算です。

また同時に、ベクトルの計算でもあります。
こういった動画の方がイメージがつかみやすいでしょうか。
Dimensions 第5章 複素数
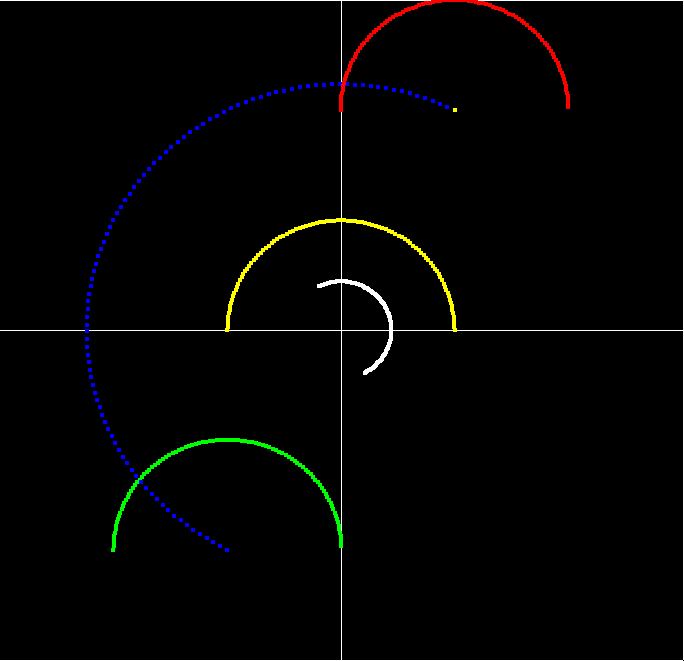
乗算,除算 = 回転と絶対値の変化
青は乗算、白は除算した結果を表しています。
黄色い点が基準になるよう青が左回転し、白がその逆方向に回転しています。
また、黄色の点が基準になるように青が拡大され、白が縮小されています。
これは、実数の値だけ拡大縮小され、虚数の値だけ回転するという複素数の性質によるものです。
虚数の値をかけるだけで画像の回転を実現したり、実数をかけるだけで拡大縮小ができてしまいます。
画像の加工で大活躍ですね!
べき乗
べき乗は複雑な計算に思えるかもしれませんが、虚数に対してのべき乗は座標上の回転量の調整に過ぎません。
先ほど載せたDimensions 第5章 複素数こちらを見ていただければわかるかと思いますが、虚数をかけることは座標上の1/4回転にあたります。
cmplx.Pow(1i, 2)
1/42 = 1/2回転、つまり実数の-1と同じです。
cmplx.Pow(1i, 1.0/2.0)
1/41/2 = 1/8回転です。
v := 1+0i //初期位置=1
c := cmplx.Pow(1i, 1.0/50.0) // 一度に(1/200)の回転
for n := 0; n < 200; n++{ //200回なので1回転
fmt.Println(real(v), imag(v))
v *= c
}
たったこれだけで半径1の円座標の計算ができてしまいます。
その他
描画は自作ツールです。
github: rcwindow
スレッドセーフなどかなり気を使っていますが、低レベルなことしか出来ません。
自由にドットを表示するだけのパッケージなので動画再生や画像の表示、加工のアニメーション等も出来ます(自動圧縮等しないので超遅い)