はじめに
マルチエージェントインタラクションとゲーム理論(Multi-agent Interaction and Games, MAIG)について学習したので、備忘録も兼ねて同分野の基礎について解説します。一部の専門用語については他の文献と訳出の齟齬があるかもしれませんがあしからず。記事の内容に誤りを発見した際はご指摘ください。
第2回となる本稿では、まず零和(ゼロサム)ゲームを扱います。その後、前回扱った戦略を発展させた混合戦略と相関戦略、さらにはミニマックス戦略とマックスミニ戦略、ミニマックス・リグレットについて説明します。
前回 ▶ 【ゲーム理論】第1回 - ナッシュ均衡とパレート最適について解説
次回 ▶ 【ゲーム理論】第3回 - 展開型ゲームについて解説(執筆中)

零和ゲームとは
チェスやポーカーのように、片方が勝つと片方が負けるという仕組みになっている2人のプレイヤーによるゲームのことを零和ゲームといいます。英語のまま「ゼロサムゲーム」と呼ばれることも多いです。
零和ゲームの例として、プレイヤー1が偶数か奇数のどちらかの数字を思い浮かべ、プレイヤー2がそれが偶数であるか奇数であるかを予測する、という零和ゲームを考えましょう。プレイヤー2が正しく予測できればプレイヤー2の効用は $1$ 、プレイヤー2が誤った予測をした場合のプレイヤー2の効用は $-1$ です。零和ゲームなので、予測が当たった場合のプレイヤー1の効用は $-1$ 、外れた場合のプレイヤー1の効用は $1$ となります。

繰り返しになりますが、零和ゲームの場合、プレイヤー1の効用とプレイヤー2の効用の和は常に $0$ となります。そのため表によってゲームを表す際は、プレイヤー1の効用のみを表記すれば二人の効用を特定するのには十分です。したがって、例えば以下のように表記を簡略化することができます。

混合戦略
前回の記事で扱った戦略は、いずれも「とり得る行動の中からどれか1つを選ぶ」という決定的なものでした。このように、一つだけの行動を選択する戦略のことを「純粋戦略」と呼びます。
しかし、戦略では必ずしも同じ行動を毎回取らなければならないというわけではありません。コインの裏表のような偶然の要素に従う戦略について考えてみましょう。
混合戦略とは
実際に取る行動を確率的に決めるような戦略のことを、混合戦略といいます。もう少し正確に言えば、混合戦略とは取りうる行動に対して定義される確率分布に従ってプレイヤーが行動を選択するような戦略のことです。
$n$ 人のプレイヤーが参加する標準形ゲーム $(N,\,A,\,u)$ に対して混合戦略を $s=(s_1,\,s_2,\,\cdots,\,s_n)$ と定義します。$s_i:\,A_i\mapsto [0,\,1]$ は任意の $i$ に対して
$$
\sum_{a\in A_i}s_i\,(a)=1
$$
を満たす、「$i$ 番目のプレイヤーがある行動を取る確率を与える関数」です。
このとき、混合戦略 $s$ についてのプレイヤー $i$ の期待効用(効用の期待値)は以下のように表すことができます。
$$
u_i(s)=\sum_{a\in A}u_i\,(a)\prod_{j=1}^{n}s_j\,(a_j)
$$
$a$はプレイヤー全員の行動の組 $(a_1,\,a_2,\,\cdots,\,a_n)$ であったことを思い出せば、飲み込みやすい式なのではないでしょうか。
混合戦略におけるナッシュ均衡
零和ゲームの章で紹介した「数当てゲーム」をもう一度見てみましょう。前回扱った純粋戦略のみを考えた場合、このゲームにナッシュ均衡は存在するでしょうか。
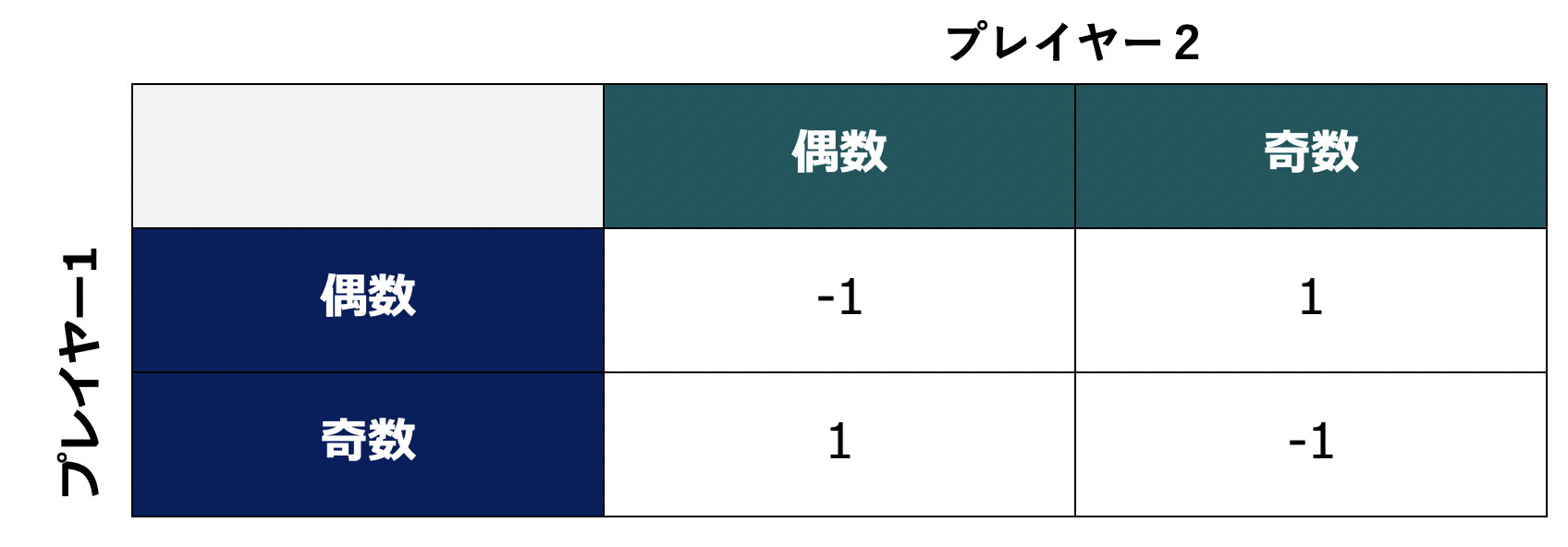
例えばプレイヤー1が偶数、プレイヤー2が偶数をそれぞれ選ぶ状況はナッシュ均衡になるでしょうか。プレイヤー1にとっては、プレイヤー2が偶数を選ぶとわかっている状況のもとでは奇数を選択したほうが効用が高いです。ではプレイヤー1が奇数、プレイヤー2が偶数を選ぶ場合はどうかというと、今度はプレイヤー2にとっては奇数を選んだほうが効用が高くなります。同様に一つ一つ確かめてみればわかりますが、明らかにこのゲームに純粋戦略のナッシュ均衡は存在しませんね。
混合戦略を用いた均衡について考えてみましょう。プレイヤー1が偶数を選択する確率を $p_e$、奇数を選択する確率を $p_o$ と表します。同様に、プレイヤー2が偶数を選択する確率を $q_e$ 、奇数を選択する確率を $q_o$ と表します。また、表記の簡略化のため「偶数を選択する」という行動を $e$ 、「奇数を選択する」という行動を $o$ と表しましょう。
$p_e,\,p_o,\,q_e,\,q_o$ に従う戦略がナッシュ均衡となるとき、プレイヤー1にとって「自身が偶数を選択したときの期待効用」と「自身が奇数を選択したときの期待効用」は等しくなる必要があります1。ゆえに、以下の式が成り立ちます。左辺が「プレイヤー1が偶数を選択したときのプレイヤー1の期待効用」、右辺が「プレイヤー1が奇数を選択したときのプレイヤー1の期待効用」です。
$$
\begin{align}
-1\cdot q_e+1\cdot q_o=1\cdot q_e+-1\cdot q_o\tag{1}
\end{align}
$$
同様に、プレイヤー2にとって「自身が偶数を選択したときの期待効用」と「自身が奇数を選択したときの期待効用」は等しくなる必要があります。よって先ほどと同様に、以下の式が成り立ちます。
$$
\begin{align}
1\cdot p_e+-1\cdot p_o=-1\cdot p_e+-1\cdot p_o\tag{2}
\end{align}
$$
また、プレイヤー1とプレイヤー2はそれぞれ偶数か奇数のどちらかを必ず選択するので、$p_e,\,p_o,\,q_e,\,q_o$ は以下の式を満たします。
$$
\begin{align}
p_e+p_o=1\tag{3}\\
q_e+q_0=1\tag{4}
\end{align}
$$
以上の(1)〜(4)式を連立すると、混合戦略におけるナッシュ均衡を与える$p_e,\,p_o,\,q_e,\,q_o$ は
$$
p_e=p_o=q_e=q_o=\frac{1}{2}
$$
と求まります。つまり、両者がそれぞれ等確率でランダムに奇数か偶数を選択するような戦略が、数字当てゲームにおけるナッシュ均衡です。
混合戦略の性質
混合戦略におけるナッシュ均衡の別の例を見てみましょう。プレイヤー1とプレイヤー2がサッカーをするか野球をするかを決める、下表のようなゲームを考えます。
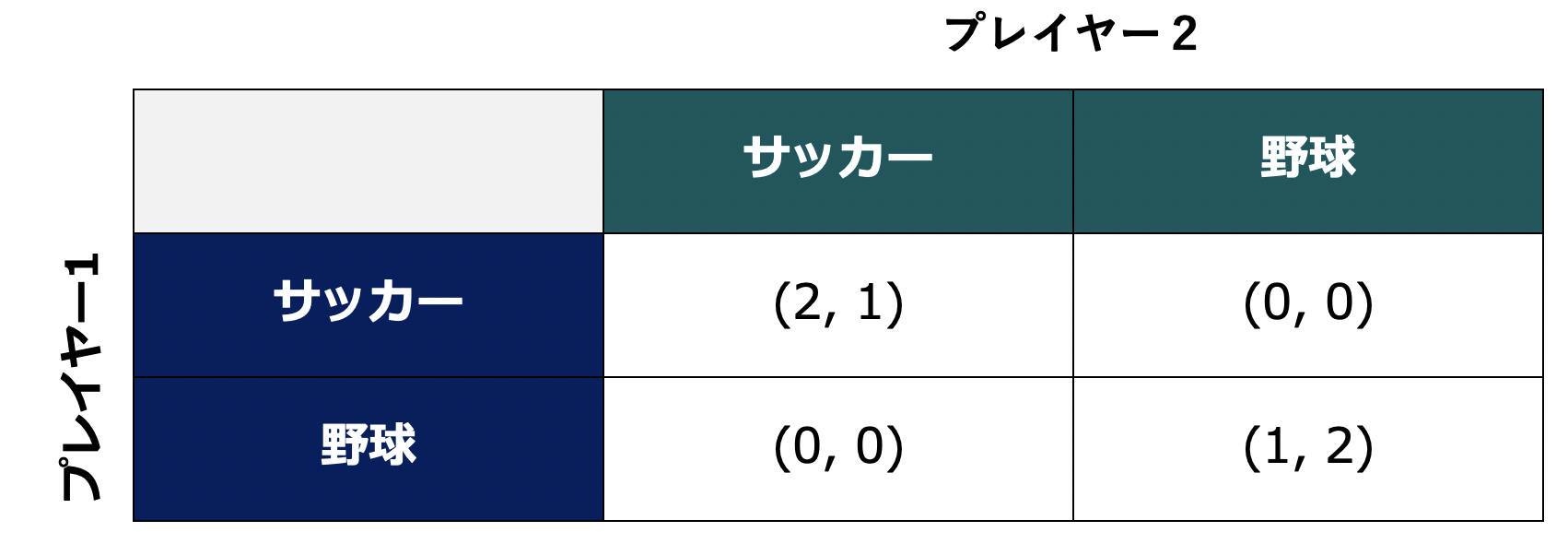
プレイヤー1はサッカーの方が好きですが、プレイヤー2は野球のほうが好きです。ただし二人の希望が食い違うとどちらも効用は $0$ になってしまう、というようなシチュエーションです。このゲームにおける純粋戦略のナッシュ均衡は、下図で黄色く示した2マスですね。

さて、混合戦略におけるナッシュ均衡を求めてみましょう。プレイヤー1がサッカーを選ぶ確率を $p_s$、野球を選ぶ確率を $p_b$、プレイヤー2がサッカーを選ぶ確率を $q_s$、野球を選ぶ確率を $q_b$とそれぞれ表します。数字当てゲームの際と同様に立式すると、
$$
\begin{align}
\begin{cases}
&p_b+p_s=1\\
&q_b+q_s=1\\
&1\cdot p_s+0\cdot p_b=0\cdot p_s+2\cdot p_b\\
&2\cdot q_s+0\cdot q_b=0\cdot q_s+1\cdot q_b\\
\end{cases}
\end{align}
$$
と立式できます。これらを連立すると、
$$
\begin{align}
p_b=q_s=\dfrac{1}{3}\\
p_s=q_b=\dfrac{2}{3}
\end{align}
$$
が得られます。これが混合戦略におけるナッシュ均衡です。さて、このナッシュ均衡における期待効用はいくらでしょうか。

求まった混合戦略におけるナッシュ均衡に従った際、それぞれの行動の組が実現する確率は上表の通りとなります。したがって、プレイヤー1の期待効用は
$$
2\cdot\dfrac{2}{9}+0\cdot\dfrac{1}{9}+0\cdot\dfrac{4}{9}+1\cdot\dfrac{2}{9}=\dfrac{2}{3}
$$
です。同様にプレイヤー2の期待効用も $2\,/\,3$ となります。一方、純粋戦略のナッシュ均衡における効用は悪くても $1$ です。純粋戦略における $2$ つのナッシュ均衡はどちらも、混合戦略におけるナッシュ均衡をパレート支配しています。
純粋戦略におけるナッシュ均衡は、混合戦略におけるナッシュ均衡をパレート支配することがあります。ただし、必ずしもそうなるというわけではなく、混合戦略におけるナッシュ均衡が純粋戦略におけるナッシュ均衡をパレート支配する場合もあります。
相関戦略
混合戦略では両者が独立した偶然によって行動を選択していました。それでは、両者が独立でない偶然の要素に従って行動を選択するような場合はどうでしょうか。ここでは、両者が1つの偶然の要素に従って行動するという相関戦略の概念について説明します。
相関戦略とは
相関戦略とは、複数のプレイヤーが「共通して観察できる偶然の結果」に基づいて行動を決定するような戦略のことです。先述した数当てゲームにおける例を考えてみます。

二人が行動を選択する前に一枚のコインを投げるとします。相関戦略の例としては、
- コインの表が出た場合、プレイヤー1は偶数を、プレイヤー2は奇数を選択する
- コインの裏が出た場合、プレイヤー1は奇数を、プレイヤー2は偶数を選択する
といったものが考えられます。
相関均衡
ある一つの偶然の要素に基づいた一定のルールに従ってそれぞれのプレイヤーが行動を選択する場合を考えます。すべてのプレイヤーについて、他の任意のルールに従ったとき以上の期待効用が得られる場合、それは相関均衡であるといいます。
もう少し正確に定義しましょう。$n$ 人のプレイヤーを持つ標準形ゲーム $G=(N,\,A,\,u)$ を考えます。集合 $D_i$ を集めたタプル $D$ を $D=(D_1,\,D_2,\,\cdots,\,D_n)$ とし、$d_i\in D_i$ であるとします。また、$\pi$ を $D$ 上の確率分布とします。また、$\sigma=(\sigma_1,\,\sigma_2,\,\cdots,\,\sigma_n)$ を $\sigma_i:\,D_i\mapsto A_i$ なる写像のタプルとします。このとき、任意のプレイヤー $i$ と$\sigma'_i:\,D_i\mapsto A_i$ なる任意の写像 $\sigma'_i$ に対して、
$$
\begin{align}
&\sum_{d\in D}\pi(d)\, u_i(\sigma_1(d_1),\,\cdots,\,\sigma_i(d_i),\,\cdots,\,\sigma_n(d_n))\geq \\
&\sum_{d\in D}\pi(d)\, u_i(\sigma_1(d_1),\,\cdots,\,\sigma'_i(d_i),\,\cdots,\,\sigma_n(d_n))
\end{align}
$$
が成立するとき、タプル $(D,\,\pi,\,\sigma)$ は相関均衡である、といいます。この数式だけでは意味が取りにくいかもしれません。噛み砕いて説明すると、
- 全員に共通する確率分布 $\pi$ にしたがって集合 $D_i$ の中からそれぞれランダムな要素を選び、それぞれのプレイヤーは一定のルールに従って、与えられた $d_i$ を基に行動を決める
- 今よりも良いルールが誰にも存在しないとき、相関均衡である
ということです。以下の例を見てさらに理解を深めましょう。
相関均衡の例
例えば、先程も登場した野球かサッカーを選択するゲームにおける相関均衡の例としては、
- コイントスで表が出たらプレイヤー1とプレイヤー2は共にサッカーを選択する
- コイントスで裏が出たらプレイヤー1とプレイヤー2は共に野球を選択する
先程の数式に当てはめてみましょう。2人のプレイヤーがいるため $N={1,\,2}$ となります。サッカーを $S$、野球を $B$ でそれぞれ表すと、行動は $A_1=A_2={S,\,B}$ です。
コインの表を $H$、コインの裏を $T$ とそれぞれ表すと、$D_1=D_2={H,\,T}$ です。また、コイントスに用いるコインは表裏がそれぞれ $1\,/\,2$ の確率で出るとします。このとき、$\pi(H,\,H)=\pi(T,\,T)=1\,/\,2$です。$\pi(H,\,T)$ と $\pi(T,\,H)$ は1枚のコインの表と裏が同時に出ることを意味しているため、どちらも $0$ です。
コイントスで表が出た場合、プレイヤー1とプレイヤー2はどちらもサッカーを選択するため、$\sigma_1(H,\,H)=\sigma_2(H,\,H)=S$ となります。裏が出た場合は共に野球を選択するため、同様に $\sigma_1(T,\,T)=\sigma_2(T,\,T)=S$ です。相関均衡の定義式が理解できなかった場合は、以上の例と照らし合わせながら確認すると意味が分かるはずです。
相関均衡の性質
先述した相関均衡における期待効用を計算してみましょう。コインは表裏がそれぞれ $1\,/\,2$ の確率で出ると仮定したため、プレイヤー1の期待効用は
$$
2\cdot\dfrac{1}{2}+1\cdot\dfrac{1}{2}=\dfrac{3}{2}
$$
となります。プレイヤー2の期待効用も、同様に計算すると $3\,/\,2$ と求まります。混合戦略のナッシュ均衡における両者の期待効用はそれぞれ $2\,/\,3$ であったため、相関均衡の期待効用のほうが高くなっていますね。
相関均衡は、ナッシュ均衡を一般化した概念であることが知られています。すなわち、ナッシュ均衡が存在する場合、それに対応する相関戦略が存在します2。
種々の戦略
ここまで紹介してきたナッシュ均衡などは、どれも互いのプレイヤーが合理的な選択をするという仮定に基づいたものでした。ここからは相手が非合理的な選択をしうる場合にも有効な、マックスミニ戦略とミニマックス戦略、ミニマックス・リグレットについて説明します。
マックスミニ戦略
マックスミニ戦略は、自身の獲得しうる利得の最小値を最大化する戦略です。純粋戦略におけるマックスミニ戦略を考えてみます。
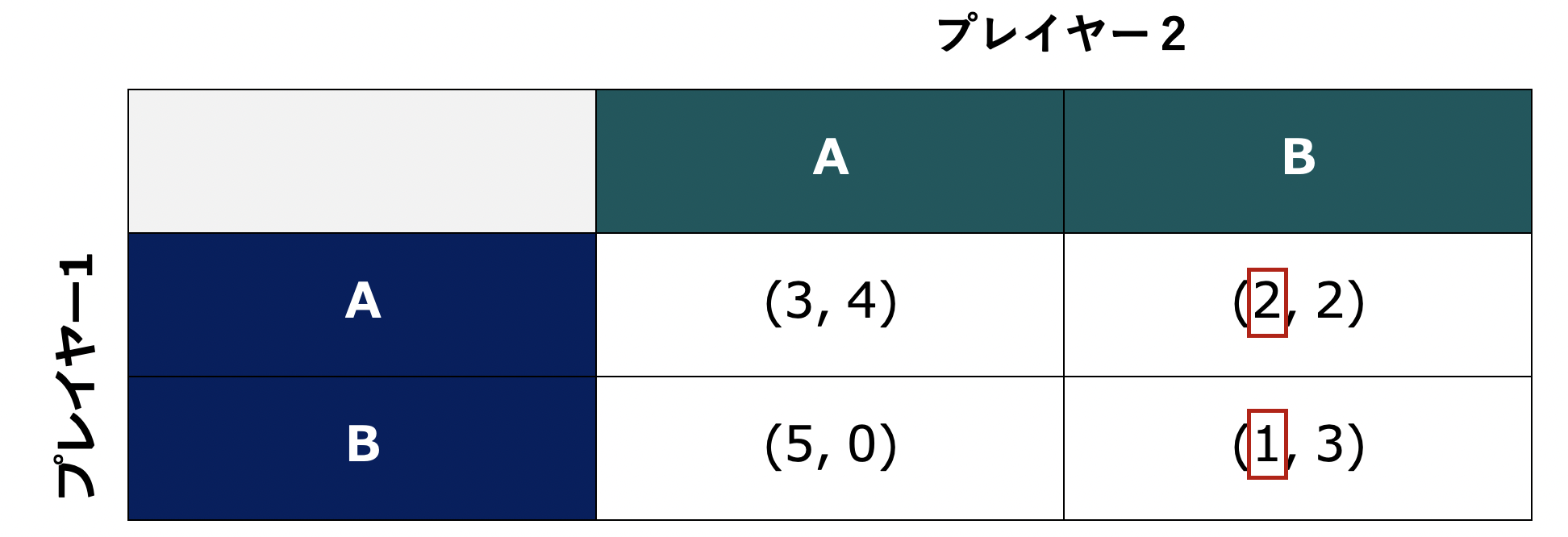
上表のようなゲームを考えましょう。まずはプレイヤー1が行動 $A$ を選択する場合について考えます。このとき、プレイヤー2が $A$ を選択した場合の効用は $3$、プレイヤー2が $B$ を選択した場合の効用は $2$ です。したがって、プレイヤー1が行動 $A$ を選択する場合の最小効用は $2$ となります。同様に、プレイヤー1が行動 $B$ を選択する場合の最小効用は $1$ です。これらを上図では赤枠で示しています。
両者を比較すると、プレイヤー1の最小効用が高くなる行動は $A$ であることがわかりますね。したがって、プレイヤー1が最小効用を最大化しようとする場合、選択する行動は $A$ となります。これがマックスミニ戦略です。なお、マックスミニ戦略を取る際、考えられる効用の最小値のことを「マックスミニ値」と呼びます。先程の例の場合、プレイヤー1にとってのマックスミニ値は $2$ です。
混合マックスミニ戦略
混合戦略についてもマックスミニ戦略を考えることができます。再び、サッカーか野球を選択するゲームについて考えてみましょう。プレイヤー1がサッカーを選択する確率を $p_S$、プレイヤー2がサッカーを選択する確率を $q_S$ とします。
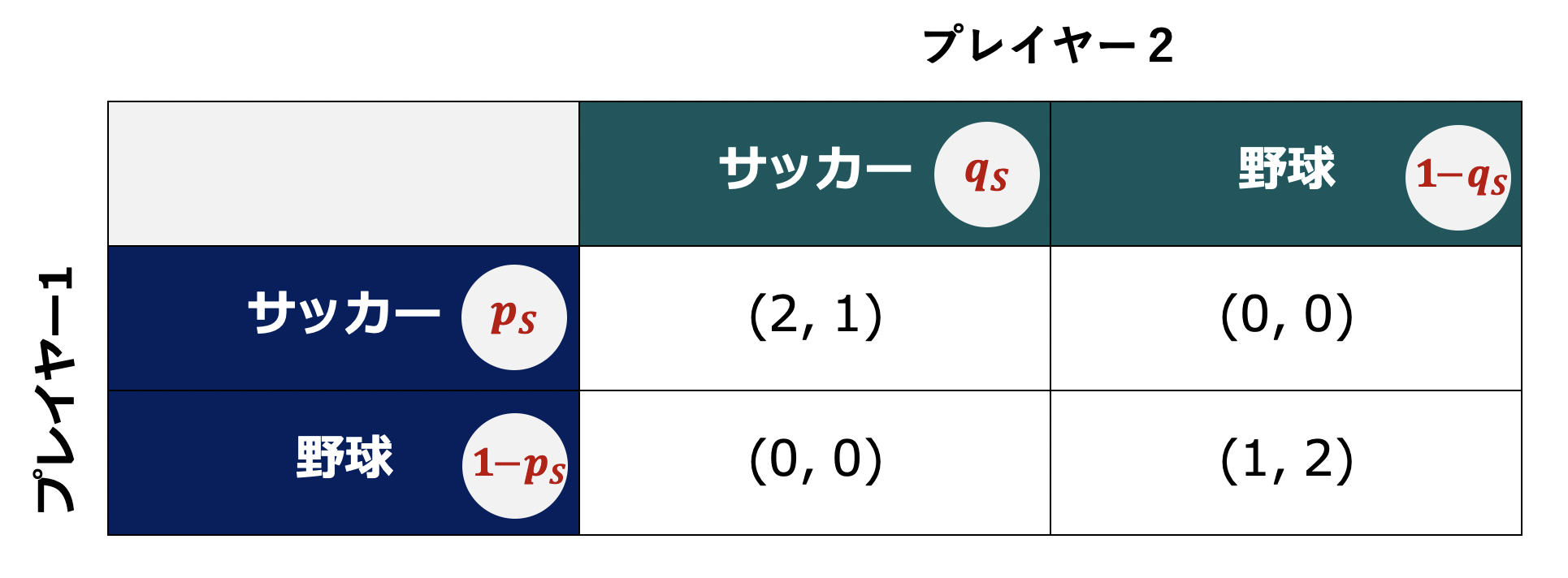
このとき、プレイヤー1の期待効用は
$$
\begin{align}
&2\cdot p_S q_S+1\cdot (1-p_S)(1-q_S)\\
&=3p_S q_S-p_S-q_S+1\\
&=(3p_S-1)q_S-p_S+1
\end{align}
$$
と表すことができます。このときマックスミニ戦略を与える $p_S$ は
$$
\arg\max_{p_S\in[0,\,1]}[\min_{q_S\in[0,\,1]}\{(3p_S-1)q_S-p_S+1\}]
$$
と表せますね。具体的に $q_s\in [0,\,1]$ を計算すると、
$$
\begin{cases}
&q_s=0\quad&\left(\dfrac{1}{3}\leq p_S\leq 1\right)\\
&q_s=1\quad&\left(0\leq p_S\leq \dfrac{1}{3}\right)
\end{cases}
$$
となります。このときプレイヤー1の期待効用は以下の通りです。
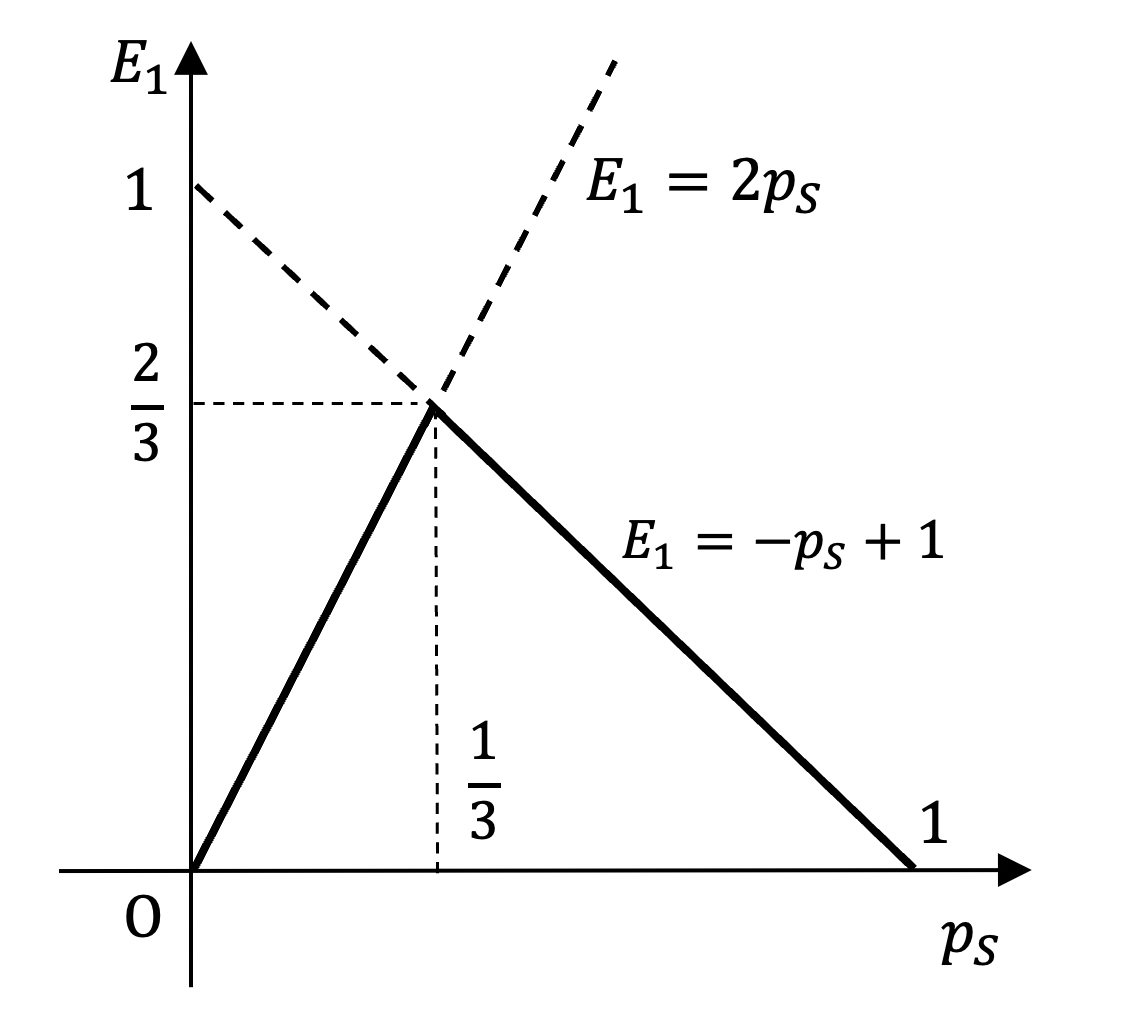
$$
\begin{cases}
&-p_S+1\quad&\left(\dfrac{1}{3}\leq p_S\leq 1\right)\\
&2p_S\quad&\left(0\leq p_S\leq \dfrac{1}{3}\right)
\end{cases}
$$
ゆえに以下のグラフから、このときのプレイヤー1の期待効用の最大値は $p_S=1\,/\,3$ のときの $2\,/\,3$ と求まります。横軸に $p_S$、縦軸に期待効用 $E_1$ を取っています。
ミニマックス戦略
ミニマックス戦略は、マックスミニ戦略とは反対に「相手が得る利得の最大値を最小化する」戦略です。この場合、自分の利得は度外視して、相手の最大利得を最小化することのみを考えます。
例えば下表に示すゲームを考えましょう。
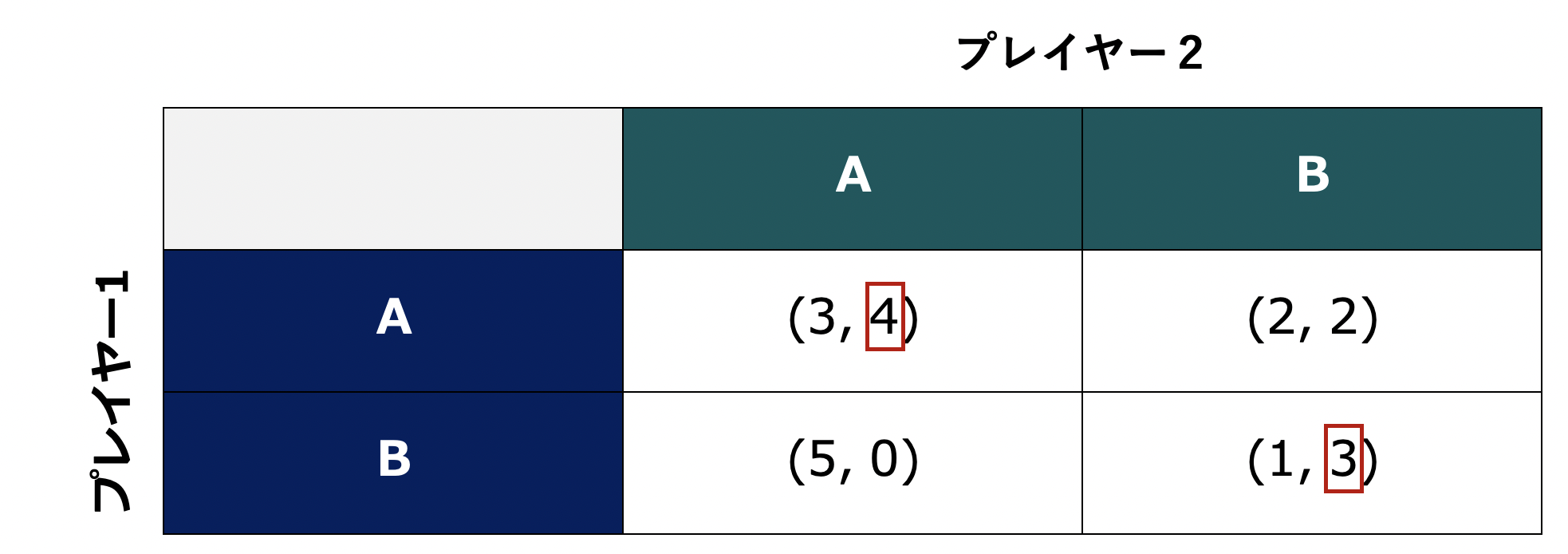
プレイヤー1の視点に立ちます。もし自分が行動 $A$ を選択した場合、プレイヤー2の最大効用は $4$ です。もし自分が行動 $B$ を選択した場合、プレイヤー2の最大効用は $3$ です。表ではそれぞれ赤枠で示しています。プレイヤー1は相手の最大効用を最小化したいため、ミニマックス戦略を採用する場合、プレイヤー1は行動 $B$ を選ぶことになります。
なお、マックスミニ戦略と同様に、ミニマックス戦略についても混合戦略を考えることができます。
有限な二人零和ゲームにおいてはどちらのプレイヤーに対しても、ミニマックス戦略において得られる戦略とマックスミニ戦略において得られる戦略が一致します。これは、1928年にノイマンによって証明された「ミニマックス定理」として知られています。
ミニマックス・リグレット
本稿の最後に、ミニマックス・リグレット戦略について紹介します。ミニマックス・リグレットは、最も悪いケースの損失(正確には後述するリグレット)を最小化する戦略です。最も悪いケースの利得を最大化するマックスミニ戦略と似ていますが、一般にはマックスミニ戦略と異なる戦略が得られます。
リグレットとは
ミニマックス・リグレット戦略の解説に入る前に、リグレット(後悔)について説明します。リグレットとは、自分以外のプレイヤーの行動が同じときに、自分が得られたであろう効用の最大値との差のことです。これだけだとやや分かりにくいので、具体例で説明します。
例えば、マックスミニ戦略の際にも登場した以下のゲームおいて、プレイヤー1とプレイヤー2がそれぞれ $B$ を選んだとします。この場合のプレイヤー1のリグレットについて考えてみましょう。

プレイヤー2が $B$ を選択する場合、プレイヤー1にとって最適な行動は $A$ です。もしプレイヤー1が $B$ ではなく $A$ を選択していれば、プレイヤー1は効用 $2$ を得ることができました。しかし、プレイヤー1は $B$ を選択してしまったので、実際に得た効用は $1$ です。ゆえに、このときのリグレットは $2-1=1$ となります。
数式で表してみましょう。プレイヤー $i$ が取った行動を $a_i$、プレイヤー$i$ 以外が取った行動を $a_{-i}$ で表します。このとき、プレイヤー $i$ のリグレットは以下の式で表すことができます。
$$
[\max_{a'_i\in A_i}u_i(a'_i,\,a_{-i})]-u_i(a_i,\,a_{-i})
$$
最大リグレットとは
プレイヤー $i$ にとっての最大リグレットとは、プレイヤー $i$ が行動 $a_i$ を取るとき、プレイヤー $i$ 以外が取るすべての行動の中でのリグレットの最大値を指します。こちらも例を見てみましょう。プレイヤー1が $A$ を選ぶとします。

プレイヤー2が $A$ を選ぶとき、プレイヤー1の効用は $3$、プレイヤー2が $B$ を選ぶとき、プレイヤー1の効用は $2$ となります。ゆえに、$(A,\,A)$ のリグレットは $3-3=0$、$(A,\,B)$ のリグレットは $3-2=1$ です。したがって、プレイヤー1が $A$ を選ぶ際の最大リグレットは $1$ となります。
同様に、プレイヤー1が $B$ を選ぶとします。

プレイヤー2が $A$ を選ぶとき、プレイヤー1の効用は $5$ です。プレイヤー2が $B$ を選ぶとき、プレイヤー2の効用は $1$ です。ゆえに、$(B,\,A)$ のリグレットは $5-5=0$、$(B,\,B)$ のリグレットは $5-1=4$ となり、プレイヤー1が $B$ を選ぶ場合の最大リグレットは $4$ となります。
$i$ 番目のプレイヤーが行動 $a_i$ を取るときの最大リグレットは、先程定義したリグレットの最大値となるため、以下のように表すことができます。
$$
\max_{a'_{-i}\in A_{-i}}\left([\max_{a'_i\in A_i}u_i(a'_i,\,a_{-i})]-u_i(a_i,\,a_{-i})\right)
$$
ミニマックス・リグレットとは
ミニマックス・リグレットとは、最大リグレットを最小化する戦略のことです。
先程求めた通り、プレイヤー$1$ にとって $A$ を選択した際の最大リグレットは $1$、$B$ を選択した際の最大リグレットは $4$ でした。ミニマックス・リグレットにおいてはこの最大リグレットが最小となる行動を選択するため、プレイヤー1は行動 $A$ を選択します。起こりうる後悔の小さい行動を選択する、という方針ですね。

プレイヤー$i$ は自身がとり得る行動の中で、最大リグレットが最小となるような行動を取ります。そのため、ミニマックス・リグレットにおいてプレイヤー $i$ が取る行動を数式で表すと以下のようになります。
$$
\underset{a_i\in A_i}{\rm{argmin}}\,\left[\max_{a'_{-i}\in A_{-i}}\left([\max_{a'_i\in A_i}u_i(a'_i,\,a_{-i})]-u_i(a_i,\,a_{-i})\right)\right]
$$
おわりに
零和ゲームや混合戦略、相関戦略について扱いました。また、種々の戦略としてマックスミニ戦略やミニマックス戦略、さらにはミニマックス・リグレットについて紹介しました。ゲーム理論独特の考え方が多く感じるかもしれませんが、これらはいずれもゲームにおける戦略を考える上で重要な概念です。次回は展開型ゲームについて扱っていきます。
訳出について
専門用語は、Wikipediaを参考に以下のように訳出しています。
| 日本語 | 英語 |
|---|---|
| 零和ゲーム | Zero-sum Game |
| 期待効用 | Expected Utility |
| 純粋戦略 | Pure Strategy |
| 混合戦略 | Mixed Strategy |
| 相関戦略 | Correlated Strategy |
| マックスミニ戦略 | Maxmin Strategy |
| マックスミニ値 | Maxmin Value |
| 混合マックスミニ戦略 | Mixed Maxmin Strategy |
| ミニマックス戦略 | Minmax Strategy |
| リグレット | Regret |
| ミニマックス・リグレット | Minmax Regret |
参考文献
- Yoav Shoham and Kevin Leyton-Brown, "Multi-Agent Systems", Cambridge University Press(2009)
- Wikipedia, "ゲーム理論", https://ja.wikipedia.org/wiki/%E3%82%B2%E3%83%BC%E3%83%A0%E7%90%86%E8%AB%96, 最終閲覧2022/11/08
- 画像素材: Unsplash, https://unsplash.com/ja, 最終閲覧2022/11/02
なお、内容の説明にはLeibniz Universität HannoverのDaniel Kudenko先生の講義を参考にしています。
