[Python]NetworkXでQiitaのタグ関係図を描く

はじめに

Pythonのライブラリ、NetworkXの使い方を、Qiitaの投稿に付けられたタグの関係グラフの作成を例にして説明します。
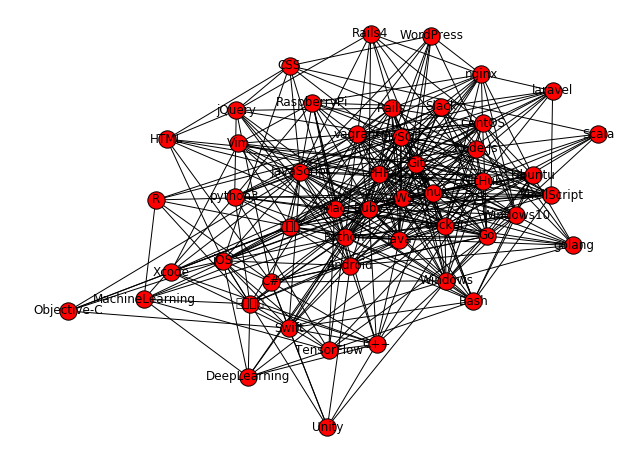
NetworkXを使うと、下に示すような、ノードとエッジで構成されるグラフを描くことができます。

##実行環境

• Windows 10
• Python 3.5.2 (Anaconda)
• Jupyter notebook

#元データの取得
Qiitaは、投稿を取得するAPIを公開しているので、簡単に投稿を取得することができます。
JSON形式で返ってくるデータを下記コードでPythonの辞書に変換します。
なお、非認証の場合、1リクエストごとに最大100記事、1時間ごとに60回の制限があるので、
今回は、100*60 = 6000 記事を対象とします。

import requests
import json

items = []
params = {"page":1, "per_page":100}
for i in range(60):
    print("fetching... page " + str(i+1))
    params["page"] = i + 1
    res = requests.get("https://qiita.com/api/v2/items", params=params)
    items.extend(json.loads(res.text))

#データの下準備
APIで取得したデータについて、タグのみを抽出して、[ [tag1, tag2], [tag3], ... ]の形式に変換します。

tags_list = []
for item in items:
    tags = [tag["name"] for tag in item["tags"]]
    tags_list.append(tags)

また、collections.Counterを用いてタグの出現回数をカウントします。
このとき、itertools.chain.from_iterable(tags_list)で多重配列をflattenしています。
あまり、ノード数が多いと図がごちゃごちゃするので、上位50タグを抽出します。

import collections
import itertools

tag_count = collections.Counter(itertools.chain.from_iterable(tags_list)).most_common(50)

#NetworkXの利用
ここから、NetworkXを使って、グラフを作成していきます。
##初期化とノードの追加
G = nx.Graph()で新しいグラフをつくり、タグ名のノードを追加していきます。
後で描画時にノードの大きさを決定するために、ノードの属性に出現回数countを入れています。

import networkx as nx
G = nx.Graph()
G.add_nodes_from([(tag, {"count":count}) for tag,count in tag_count])

##エッジの追加
1つの投稿に複数のタグが含まれた場合、すべての組み合わせにエッジを追加します
例えば、この記事のように「Python, networkx, Qiita」がタグづけられている投稿があった場合、
Pythonノードとnetworkxノード間、networkxとQiita間、QiitaとPython間にエッジを作成します。
すでにエッジが存在する場合には、エッジのweightを増加させます。

for tags in tags_list:
    for node0,node1 in itertools.combinations(tags, 2):
        if not G.has_node(node0) or not G.has_node(node1):
            continue
        if G.has_edge(node0, node1):
            G.edge[node0][node1]["weight"] += 1
        else:
            G.add_edge(node0, node1, {"weight":1})

##ひとます、グラフの描画してみる
ここでいったんグラフを描いてみます。

%matplotlib inline
import matplotlib.pyplot as plt

plt.figure(figsize=(15,15))
pos = nx.spring_layout(G)
nx.draw_networkx(G,pos)

plt.axis("off")
plt.savefig("default.png")
plt.show()

よくわからないグラフができてしまいました。

##グラフ描画の調整
ここからグラフをきれいにするため、いろいろ調整していきます。

###エッジの枝刈り
出現回数が少ないエッジを削除します。

for (u,v,d) in G.edges(data=True):
    if d["weight"] <= 4:
        G.remove_edge(u, v)

###反発力の調整
pos = nx.spring_layout(G)では、ノード間の反発力と、エッジのweightの大きさによる吸引力でノードの位置が決定されます。
ノード間の反発力は、引数kを指定することで設定でき、kが大きいほどノードの配置は円形に近くなります。

pos = nx.spring_layout(G, k=0.3)

###ノードの大きさと、ノードラベルの日本語の表示
ノードの円の大きさを、countが大きいほど大きくします。
また、先ほど出力した図では、日本語が四角形になって表示されないので日本語表示可能なフォントを設定します。

node_size = [ d["count"]*20 for (n,d) in G.nodes(data=True)]
nx.draw_networkx_nodes(G, pos, node_color="w",alpha=0.6, node_size=node_size)
nx.draw_networkx_labels(G, pos, fontsize=14, font_family="Yu Gothic", font_weight="bold")

エッジの太さ

エッジのweightに応じてエッジを太くします。

edge_width = [ d["weight"]*0.2 for (u,v,d) in G.edges(data=True)]
nx.draw_networkx_edges(G, pos, alpha=0.4, edge_color="c", width=edge_width)

###描画してみるとこちら
このコードで描画します。できたグラフがしっくりくるまで何回か実行してみたり、パラメータを変更したりしてみましょう。

%matplotlib inline
import matplotlib.pyplot as plt
import math

for (u,v,d) in G.edges(data=True):
    if d["weight"] <= 4:
        G.remove_edge(u, v)
    
plt.figure(figsize=(15,15))
pos = nx.spring_layout(G, k=0.3)

node_size = [ d['count']*20 for (n,d) in G.nodes(data=True)]
nx.draw_networkx_nodes(G, pos, node_color='w',alpha=0.6, node_size=node_size)
nx.draw_networkx_labels(G, pos, fontsize=14, font_family="Yu Gothic", font_weight="bold")

edge_width = [ d['weight']*0.2 for (u,v,d) in G.edges(data=True)]
nx.draw_networkx_edges(G, pos, alpha=0.4, edge_color='C', width=edge_width)

plt.axis('off')
plt.savefig("g2.png")
plt.show()

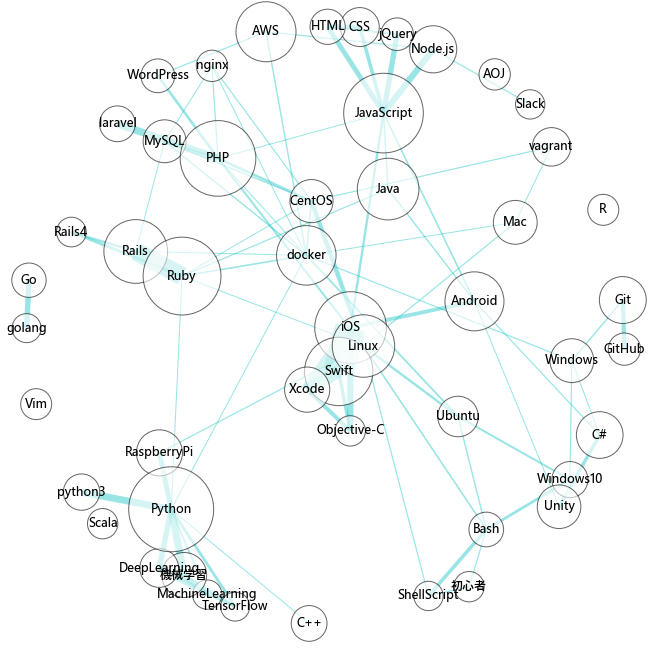
上にWeb(Ruby(on Rails), JavaScript, PHP...)関係、左下にPython(機械学習)関係、真ん中にiOS関係、右下にBashが使えるようになったWindows10の話題...といったように、人気のタグとその関係性が見える図ができました。