Python3ではじめるシステムトレード：3元分割表

3元分割表は２元分割表の単なる延長線上にあると思い、軽く見ていましたが、どうもそうではなさそうなので、少し調べてみました。統計学実践ワークブックを参考にしています。

3元分割表

3元分割表に集約されるデータについては、サンプリング方法により、因子や固定される周辺和の性質も変化する。しかし、2元分割表と同様、推定や検定を行う際の数学的な扱いは、サンプリング方式によらない。そこで、総度数が固定された多項分布モデルの場合で説明する。

質的な3つの因子 $A, B, C$ があり、簡単のため、水準数を順に $2, 2, 2$ とする。水準組合せ（$A_i, B_j, C_k$）の頻度を $x_{ijk}$ とすると $2 \times 2 \times 2$ 分割表を考え、周辺和を

$$
x_{ij.} = \sum_{k=1}^{2} x_{ijk}, \quad x_{i..} = \sum_{j=1}^{2} \sum_{k=1}^{2} x_{ijk}, \quad x_{...} = n = \sum_{i=1}^{2} \sum_{j=1}^{2} \sum_{k=1}^{2} x_{ijk}
$$

などと表す。多項分布（$222(IJK)$ 項分布）の母数を $\theta_{ijk} = P(A_i, B_j, C_k)$, $\sum_{i=1}^{2} \sum_{j=1}^{2} \sum_{k=1}^{2} \theta_{ijk} = 1$ とし、$\theta_{ij.}, \theta_{i..}$ なども同様に定める。

3つの因子については、以下のような統計モデルが考えられる。

1. すべての $ i, j, k $ について $ \theta_{ijk} = \theta_{i..}\theta_{.j.}\theta_{..k} $ が成立する。これを完全独立モデルとよび、$ A \perp B \perp C $ と書く。

2. すべての $ i, j, k $ について $ \theta_{ijk} = \theta_{i..}\theta_{.jk} $ が成立する。これを $ A $ と $ (B, C) $ の間の周辺独立モデルとよび、$ A \perp (B, C) $ と書く。

3. すべての $ i, j, k $ について $ \theta_{ijk} = \frac{\theta_{i.k}\theta_{.jk}}{\theta_{..k}} $ が成立する。これを $ C $ を与えたもとでの $ A $ と $ B $ の条件付き独立モデルとよび、$ A \perp B | C $ と書く。

ここで多項分布を使うのは分割表がカテゴリカルデータを扱うからである。

実際にデータを生成してこれら３つのモデルになるかどうかを検証する。

import numpy as np
from scipy.stats import chi2_contingency, chi2

# 乱数生成
probs = np.full((2, 2, 2), 1/8).flatten()  # 各セルの確率
counts = np.random.multinomial(1000, probs)  # 多項分布から乱数生成
data_3d = counts.reshape(2, 2, 2)  # 乱数を3次元配列に変換


def create_table(data_3d):
    # 2x2分割表
    table1 = data_3d[:, :, 0]
    table2 = data_3d[:, :, 1]

    # 周辺和を含めた表の作成
    def create_extended_table(table):
        row_sums = table.sum(axis=1, keepdims=True)
        col_sums = table.sum(axis=0, keepdims=True)
        total_sum = table.sum()

        # 表に周辺和を追加
        extended_table = np.vstack([np.hstack([table, row_sums]),
                                np.hstack([col_sums, np.array([[total_sum]])])])
        return extended_table

    # 表1と表2の拡張版を作成
    extended_table1 = create_extended_table(table1)
    extended_table2 = create_extended_table(table2)

    # 表の表示
    print("表1 (C=0) とその周辺和:")
    print(extended_table1)
    print("\n表2 (C=1) とその周辺和:")
    print(extended_table2)
create_table(data_3d)

def statistical_test(data_3d):
    # 2x2分割表
    table1 = data_3d[:, :, 0]
    table2 = data_3d[:, :, 1]

    # 完全独立モデルの検定
    chi2_stats, p_value, dof, _ = chi2_contingency(data_3d.reshape(2, -1))
    print("完全独立な3D カイ二乗テスト: Chi2 =", chi2_stats, ", p-value =", p_value)

    # 条件付き独立モデルの検定
    chi2_value1, p1, dof1, _ = chi2_contingency(table1)
    print("表1のカイ二乗テスト: Chi2 =", chi2_value1, ", p-value =", p1)

    chi2_value2, p2, dof2, _ = chi2_contingency(table2)
    print("表2のカイ二乗テスト: Chi2 =", chi2_value2, ", p-value =", p2)

    # 周辺独立モデルの検定（Aと(B, C)）
    marginal_a = np.sum(data_3d, axis=(1, 2))
    marginal_bc = np.sum(data_3d, axis=0).flatten()
    total = data_3d.sum()

    # 期待値の計算
    expected_a = marginal_a / total
    expected_bc = marginal_bc / total
    expected_product = np.outer(expected_a, expected_bc).reshape(2, 2, 2) * total

    # カイ二乗検定
    observed = data_3d
    expected = expected_product
    chi2_statistic, p_value,dofA_BC, _ = chi2_contingency(observed, correction=False, lambda_=None)
    print("A の (B, C)に対する独立性のテスト: Chi2 =", chi2_statistic, ", p-value =", p_value)
statistical_test(data_3d)

まず、生成したデータの特性を考えてみる。コード中の probs = np.full((2, 2, 2),　1/8).flatten() という行は、多項分布に関する確率分布の定義に使われている。

np.full(shape, fill_value) は、指定された形状 (shape) で、すべての要素を fill_value で埋めたNumPy配列を生成する。

• np.full((2, 2, 2), 1/8):

  • (2, 2, 2) は配列の形状を示しており、これは三次元配列で各次元に2つの要素があることを意味する。
  • • 1/8 は配列のすべての要素を 0.125 で埋める。これは、全ての組み合わせ ( (A_i, B_j, C_k) ) の出現確率が等しく、独立しているという仮定に基づいている。

• .flatten():

  • flatten() メソッドは多次元配列を一次元配列に変換する。この操作により、元の三次元配列が一次元の確率ベクトルに変換され、多項分布のサンプリングに適した形式になる。

生成された一次元配列（確率ベクトル）は、各要素が 0.125 の8要素から成り：

• 均一性: 各カテゴリの組み合わせが等しい確率で発生するため、データには偏りがない。
• 独立性: 各カテゴリの組み合わせが独立して発生すると仮定している。

周辺独立モデル $A \perp (B, C)$ は、因子 $B, C$ を、それらの水準の組合せを新たな水準とするような $22$ 水準の 1 つの因子に置き換えてできる 2 元分割表についての独立モデルにほかならない。また、条件付き独立モデル $A \perp B | C$ は、因子 $C$ の $2$ 個の水準のそれぞれについて、因子 $A, B$ の 2 元分割表を考えたとき、$2$ 個の $2 \times 2$ 分割表のすべてで独立モデルが成り立つ、と解釈することができる。さらに完全独立モデルが成立することと、$A, B, C$ についての 3 通りの条件付き独立性がすべて成立することは同値である。

結果は、条件付独立モデル、完全独立モデル、周辺独立モデルのすべてにおいて帰無仮説(独立)を否定できない。

つぎに独立でないデータを生成する。

import numpy as np
from scipy.stats import chi2_contingency

# 依存関係を持たせた確率ベクトルの設定
probs = np.array([
    0.2,  # A=0, B=0, C=0
    0.05, # A=0, B=0, C=1
    0.05, # A=0, B=1, C=0
    0.1,  # A=0, B=1, C=1
    0.05, # A=1, B=0, C=0
    0.1,  # A=1, B=0, C=1
    0.1,  # A=1, B=1, C=0
    0.35  # A=1, B=1, C=1
])

# 確認用に合計確率が1であることを確認
assert np.sum(probs) == 1.0

# 乱数生成
counts = np.random.multinomial(1000, probs)  # 多項分布から乱数生成
data_3d = counts.reshape(2, 2, 2)  # 乱数を3次元配列に変換
data_3d

print(create_table(data_3d))

この場合には3つのモデルをすべて棄却されてしまう。

つぎに一部のモデルが棄却されるようにする。

# 各条件での独立性を保証する確率分布
# 例として、C=0とC=1でのAとBの独立性を保証
p_a_given_c0 = np.array([0.7, 0.3])  # P(A | C=0)
p_b_given_c0 = np.array([0.6, 0.4])  # P(B | C=0)

p_a_given_c1 = np.array([0.4, 0.6])  # P(A | C=1)
p_b_given_c1 = np.array([0.5, 0.5])  # P(B | C=1)

p_c = np.array([0.5, 0.5])  # P(C)

# 確率分布の生成
probs = np.zeros((2, 2, 2))
for i in range(2):
    for j in range(2):
        for k in range(2):
            if k == 0:
                probs[i, j, k] = p_a_given_c0[i] * p_b_given_c0[j] * p_c[k]
            else:
                probs[i, j, k] = p_a_given_c1[i] * p_b_given_c1[j] * p_c[k]

# 確認用に合計確率が1であることを確認
assert np.sum(probs) == 1.0

# 乱数生成
counts = np.random.multinomial(1000, probs.flatten())  # 多項分布から乱数生成
data_3d = counts.reshape(2, 2, 2)  # 乱数を3次元配列に変換

# 3次元配列の表示
print("生成されたデータ:")
print(data_3d)

print(create_table(data_3d))

print(statistical_test(data_3d))

となり表１,２のカイ二乗テストは棄却される。

対数線形モデル

3 通りの独立性モデルを対数線形モデルとして特徴づけると高次の分割表への拡張を考えやすい。3元分割表の母数 $\theta_{ijk}$ についての対数線形モデル（飽和モデル）を

\log \theta_{ijk} = \mu + \alpha_i + \beta_j + \gamma_k + (\alpha \beta)_{ij} + (\alpha \gamma)_{ik} + (\beta \gamma)_{jk} + (\alpha \beta \gamma)_{ijk} \:\:\: (28.18)

と書く。ただし右辺の母数については

0 = \sum_{i=1}^{2} \alpha_i = \sum_{i=1}^{2} (\alpha \beta)_{ij} = \sum_{j=1}^{2} (\alpha \beta)_{ij} = \sum_{i=1}^{2} (\alpha \beta \gamma)_{ijk} = \sum_{j=1}^{2} (\alpha \beta \gamma)_{ijk} = \sum_{k=1}^{2} (\alpha \beta \gamma)_{ijk}

などの、「添え字についての和はすべてゼロ」という制約をおき、$\mu$ は $\sum_{i,j,k} \theta_{ijk} = 1$ から定められる基準化定数である。

実際にglmを用いて実行します。

import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.formula.api import glm

# 乱数生成部分（既にあるものを再利用）
# 前提として、data_3dが既に生成されているとします。

# データフレームに変換
data_flat = data_3d.flatten()
indices = [(i, j, k) for i in range(2) for j in range(2) for k in range(2)]
df = pd.DataFrame(indices, columns=['A', 'B', 'C'])
df['count'] = data_flat
# カテゴリカル変数として変換
df['A'] = df['A'].astype('category')
df['B'] = df['B'].astype('category')
df['C'] = df['C'].astype('category')

# データフレームの確認
print(df.head())

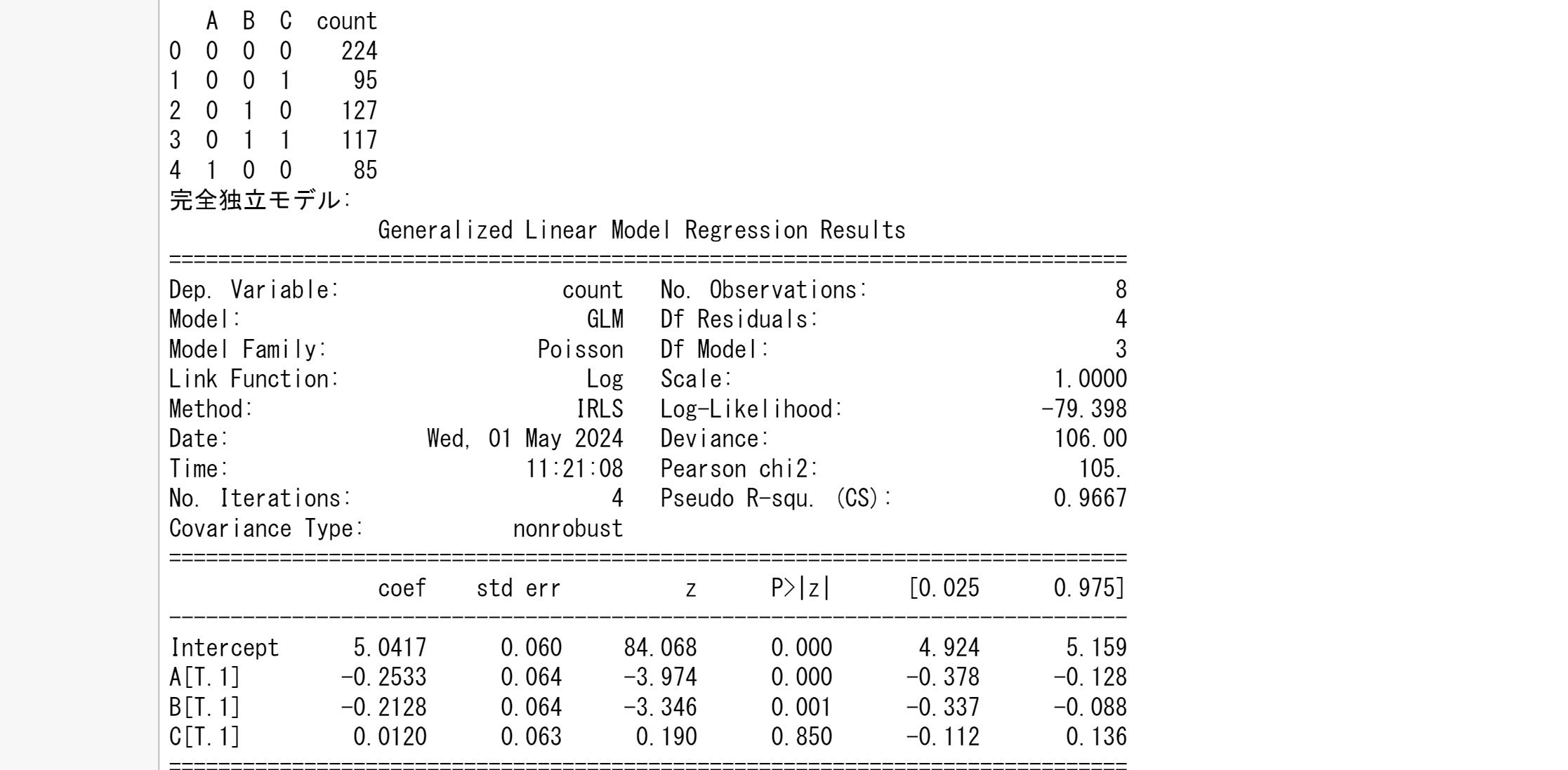
# 完全独立モデル
model_full_indep = glm('count ~ A + B + C', data=df, family=sm.families.Poisson()).fit()
print("完全独立モデル:")
print(model_full_indep.summary())

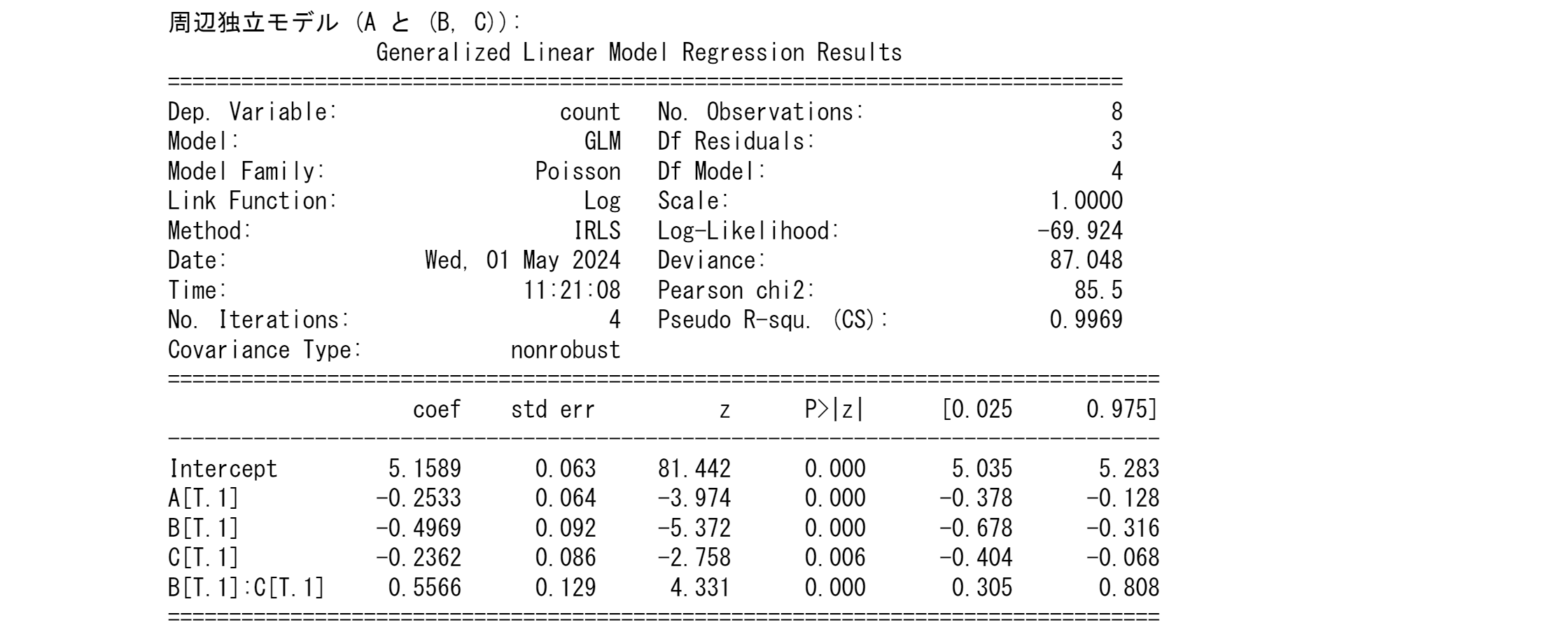
# 周辺独立モデル（例: A と (B, C)）
model_margin_indep = glm('count ~ A + B + C + B:C', data=df, family=sm.families.Poisson()).fit()
print("周辺独立モデル (A と (B, C)):")
print(model_margin_indep.summary())

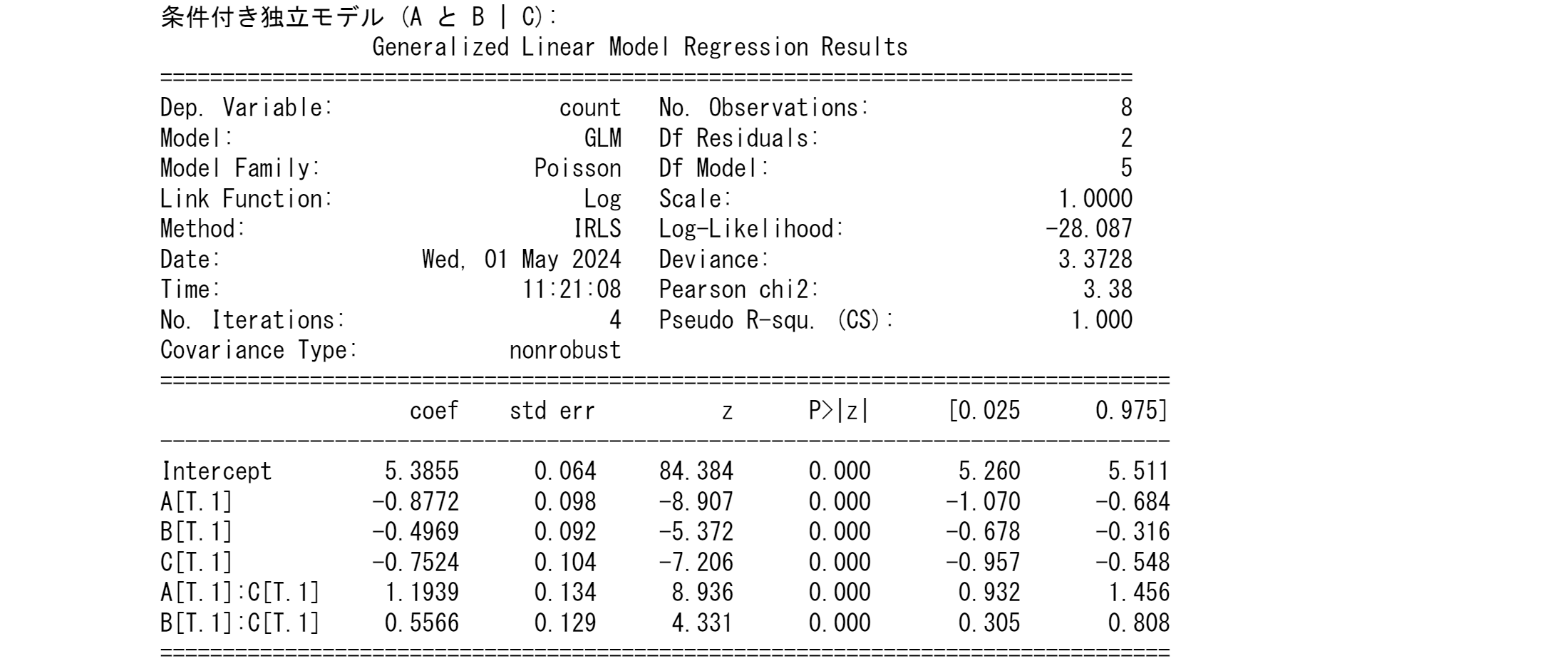
# 条件付き独立モデル（例: A と B | C）
model_cond_indep = glm('count ~ A + B + C + A:C + B:C', data=df, family=sm.families.Poisson()).fit()
print("条件付き独立モデル (A と B | C):")
print(model_cond_indep.summary())

カイ二乗検定と同じ結果になった。

ここまで読んでいただいてありがとうございます。

ここまできたらこちらもぜひ：
https://qiita.com/innovation1005/items/a9bd30c1b120078055bb
Python3ではじめるシステムトレード：カテゴリカルデータと相関行列

多項分布ではそれぞれの要因がどのような相関構造を持っているかが分かりません。そこでクラメールのVが必要になります。

Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。