単振り子
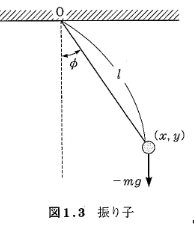
図1.3 (宮下:解析力学 裳華房 p.5)
細くて重さの無い長さ$l$の糸の先に重りを吊り下げたものを単振り子という。おもりに働く力は地球が引く力(mg)と糸が引く力である。
おもりの軌道の接線方向に働く力は$mg \sin \phi$
また
$\sin \phi = x/l$
なので, ニュートンの運動方程式は
$ma=mg \sin \phi = mg \frac{x}{l}$
単振動は等速円運動する質点の位置をある座標軸上に正射影した運動である。これは
- 振動数$f$
- 周期$T=1/f$
角速度$\omega=2\frac{\pi}{T}=2\pi f$
をもちいて、変位 $x=A \sin \omega t$
速度 $v=\omega A \cos \omega t$
加速度 $a=-\omega^2A \sin \omega t =-\omega^2 x$
で表現される。これは
$\ddot{x}=-kx$
の一般解として
$x=A \sin \omega t$
であるととらえることができる。単振り子の動きは
$\ddot{x}=g \frac{x}{l}=-kx$
と書き換えることができるので、単振動であると解釈できる。
振り子のラグランジアンを直交座標(x,y)で表現。
(2章の例p.11)
運動エネルギーは$T=1/2m\dot{x}^2+1/2m\dot{y}^2$、ポテンシャルエネルギーは$U=mgy$
したがって、ラグランジアンは
$L=\frac{m}{2}(\dot{x}^2+\dot{y}^2)-mgy$
また、ここには束縛条件
$x^2+y^2=l^2$
があるが、ここでは表現されていない。
振り子のラグランジアンを極座標(l,Φ)で表現。
(2章の例p.12)
$x=l\sin \phi$
$y=-l\cos \phi$
より、$x$と$y$を時間で微分して
$\dot{x}=\dot{l}\sin \phi + l\dot{\phi}\cos \phi$
$\dot{y}=-\dot{l}\cos \phi + l\dot{\phi}\sin \phi$
したがって
$\frac{m}{2}(\dot{x}+\dot{y})^2=\frac{m}{2}(\dot{l}\sin \phi + l\dot{\phi}cos \phi)^2+(-\dot{l}\cos \phi + l\dot{\phi}\sin \phi)^2=\frac{m}{2}(\dot{l}^2+l^2 \dot{\phi}^2)$
$U=mgl\cos \phi$
$l$は一定なので
$L=\frac{m}{2}(l^2 \dot{\phi}^2)+mgl\cos \phi$
運動方程式
オイラー・ラグランジュの運動方程式は
$\frac{d}{dt}\frac{\partial L}{\partial \dot{\phi}}=ml^2\ddot{\phi}$
$\frac{\partial L}{\partial \phi}=-mgl\sin \phi$
$\therefore$
$\ddot{\phi}=-\frac{g}{l}\sin \phi$
運動方程式の解
Φ=0近辺での微小振動の解
$sin \theta$をテイラー展開すると
$sin \theta=\theta-\frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5+ \cdots$
1次まで用いると
$\ddot{\phi}=-\frac{g}{l}\phi$
この方程式の一般解は
$\phi=A\cos(\sqrt{\frac{g}{l}}t+B)$
$\phi=\phi_0<<1, \ \dot{\phi}=0$とすると
$A=\phi_0, \ \dot{\phi}=A\frac{g}{l}\sin(B)=0 \therefore B=0$
したがって、
$\phi=\phi_0 \cos(\sqrt{\frac{g}{l}}t)$
- 微小振動のアニメーションの作成
%matplotlib inline
from numpy import sin, cos
from scipy.integrate import solve_ivp
from matplotlib.animation import FuncAnimation
import matplotlib.pyplot as plt
import numpy as np
g = 9.8 # 重力加速度 [m/s^2]
l = 1.0 # 振り子の長さ [m]
t_span = [0,20] # 観測時間 [s]
dt = 0.05 # 間隔 [s]
t = np.arange(t_span[0], t_span[1], dt)
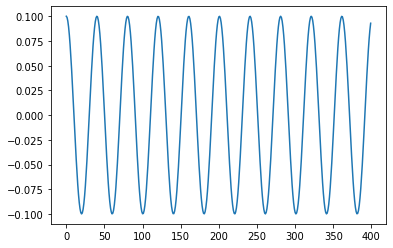
phi_0 = 0.1 # 初期角度 [deg]
phi=phi_0*cos(np.sqrt(g/l)*t)
plt.plot(phi)
x = l * sin(phi)
y = -l * cos(phi)
fig, ax = plt.subplots()
line, = ax.plot([], [], 'o-', linewidth=2)
def animation(i):
thisx = [0, x[i]]
thisy = [0, y[i]]
line.set_data(thisx, thisy)
return line,
ani = FuncAnimation(fig, animation, frames=np.arange(0, len(t)), interval=25, blit=True)
ax.set_xlim(-l,l)
ax.set_ylim(-l,l)
ax.set_aspect('equal')
ax.grid()
ani.save('pendulum.gif', writer='pillow', fps=15)
plt.show()
任意のΦを初期値とするの振動の解を求める。
$\ddot{\phi_1}=-\frac{g}{l}\sin(\phi_1)$
ここで$\phi_1=\phi+\phi_0$
この方程式の解はPythonの数値解析により容易に求めることができる。
2階の微分方程式を1階の微分方程式にする必要がある。
$\dot{\phi}=\omega$
$\dot{\omega}=-\frac{g}{l}\sin \phi$
Pythonではscipy.integrate.solve_ivpを用いる。これは初期値を与えた常微分方程式の積分を与える。
scipy.integrate.solve_ivp(fun, t_span, y0, method='RK45', t_eval=None, dense_output=False, events=None, vectorized=False, args=None, **options)
において
fun:関数
t_span:積分の範囲
y0:初期値
method:'RK45 陽的ルンゲ‐タック法
t_eval:計算結果を保存する時間
- 振動のアニメーションの作成
g = 10 # 重力加速度 [m/s^2]
l = 1 # 振り子の長さ [m]
def models(t, state):# 運動方程式
dy = np.zeros_like(state)
dy[0] = state[1]
dy[1] = -(g/l)*sin(state[0])
return dy
t_span = [0,20] # 観測時間 [s]
dt = 0.05 # 間隔 [s]
t = np.arange(t_span[0], t_span[1], dt)
phi_0 = 90.0 # 初期角度 [deg]
omega_0 = 0.0 # 初期角速度 [deg/s]
state = np.radians([phi_0, omega_0]) # 初期状態
results = solve_ivp(models, t_span, state, t_eval=t)
phi = results.y[0,:]
plt.plot(phi)
x = l * sin(phi)
y = -l * cos(phi)
fig, ax = plt.subplots()
line, = ax.plot([], [], 'o-', linewidth=2) # このlineに次々と座標を代入して描画
def animation(i):
thisx = [0, x[i]]
thisy = [0, y[i]]
line.set_data(thisx, thisy)
return line,
ani = FuncAnimation(fig, animation, frames=np.arange(0, len(t)), interval=25, blit=True)
ax.set_xlim(-l,l)
ax.set_ylim(-l,l)
ax.set_aspect('equal')
ax.grid()
plt.show()
ani.save('pendulum.gif', writer='pillow', fps=15)
ハミルトン形式
これをハミルトン形式に書き直すと
$H=p_\phi \dot{\phi}-L=\frac{m}{2}(l^2 \dot{\phi}^2)-mgl\cos \phi$
ここで
$p_\phi=\frac{m}{2}(l^2\dot{\phi})$
ハミルトン方程式は
$\dot{\phi}=\frac{\partial H}{\partial p_\phi}=\frac{p_φ}{ml^2}$
$\dot{p_\phi}=-\frac{\partial H}{\partial \phi}=mgl \sin \phi$
ここにはラグランジアンでは表現できない情報が含まれている。初期条件を変えるの振子の動きは変わる。その情報がハミルトニアンにはすべて含まれている。
import numpy as np
import matplotlib.pyplot as plt
xmax = np.pi*2.0 # setting range for grid
ymax = 2
fac=1.01 # so plotting area is slightly larger than grid
X,Y = np.meshgrid(np.arange(-xmax,xmax,.01),np.arange(-ymax,ymax,.01) )
m=1
l=30
g=9.8
H = 1/2*m*l**2*Y*Y - m*g*l*np.cos(X) #here is the Hamiltonian
U = m*l**2*Y
V = -m*g*l*np.sin(X)
plt.figure()
plt.xlabel('x')
plt.ylabel('dx/dt')
plt.axis([-xmax*fac, xmax*fac,-ymax*fac,ymax*fac])
plt.streamplot(X,Y,U,V,arrowsize=0,minlength=0.25)
図の円の中心は振子の静止状態を表している。丸い円は左右に振れる振子の動きを表している。そして、波のような曲線は回転運動を表している。
ラグランジアンでは運動は軌道によって与えられ、軌道は時間に関して2階の微分方程式である。運動を決定するにはある時刻の位置と速度が必要である。また運動方程式は軌道の微小変化をもとに変分原理から与えらる。したがって、アニメーションでは位置のみで表現されている。一方ハミルトニアンでは位置とそれに共益な運動量の空間を用いて運動を一階の微分方程式としてとらえている。この場合も変分原理を用いて運動方程式を得るのであるが、位置と速度の微小変化を変分としている。したがって、アニメーションは位置と速度で表示できるのである。円で表示される位置と速度の関係は振子が中心の位置(真下向き)にあるときには速度は最速で振り切った時の反転する瞬間はゼロになることを示している。
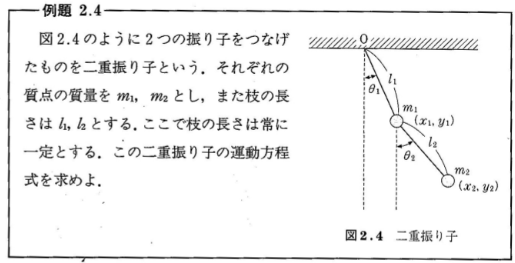
2章
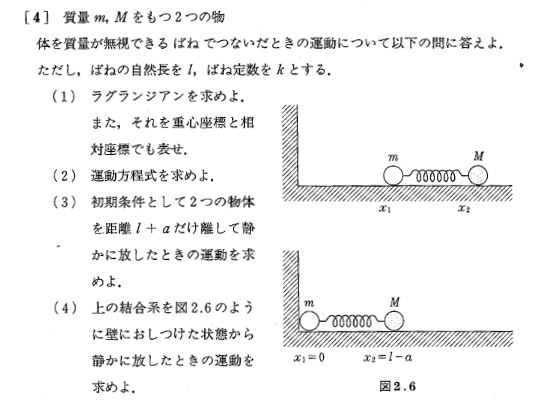
質点の座標をそれぞれ($x_1,y_1$)、($x_2,y_2$)とすると, この系の運動エネルギーは
$T=\frac{m_1}{2}(\dot{x_1}^2+\dot{y_1}^2)+\frac{m_2}{2}(\dot{x_2}^2+\dot{y_2}^2)$
位置のエネルギーは
$U=m_1gy_1+m_2gy_2$
また、束縛条件は
$x_1^2+y_1^2=l_1^2$,
$(x_2-x_1)^2+(y_2-y_1)^2=l_2^2$
である。ラグランジアンをもとめて運動方程式を解くにはラグランジュの未定定数を使う必要がある。そこでこの場合にも極座標を使うことにする。
$x_1=l_1\sin \theta_1$
$y_1=l_1\cos \theta_1$
$x_2=l_1\sin \theta_1+l_2\sin \theta_2$
$y_2=l_1\cos \theta_1+l_2\cos \theta_2$
$l_1, \ l_2$は一定であるので、それぞれを時間微分して
$\dot{x_1}=l_1\dot{\theta_1}\cos \theta_1$
$\dot{y_1}=-l_1\dot{\theta_1}\sin \theta_1$
$\dot{x_2}=l_1\dot{\theta_1}\cos \theta_1+l_2\dot{\theta_2}\cos \theta_2$
$\dot{y_2}=-l_1\dot{\theta_1}\sin \theta_1-l_2\dot{\theta_2}\sin \theta_2$
運動エネルギーは
$T_1=\frac{m_1}{2}l_1^2\dot{\theta_1}^2(\sin^2\theta_1+\cos^2\theta_1)=\frac{m_1}{2}l_1^2\dot{\theta_1}^2$
$T_2=\frac{m_2}{2}[(l_1\dot{\theta_1}\sin\theta_1 +l_2\dot{\theta_2}\sin\theta_2 )^2+(-l_1\dot{\theta_1}\cos\theta_1-l_2\dot{\theta_2}\cos\theta_2 )^2]$
$\ =\frac{m_2}{2}(l_1^2\dot{\theta_1}^2\sin^2\theta_1+2l_1l_2\dot{\theta_1}\dot{\theta_2}\sin\theta_1\sin\theta_2+l_1^2\dot{\theta_2}^2\sin^2\theta_2+l_1^2\dot{\theta_1}^2\cos^2\theta_1+2l_1l_2\dot{\theta_1}\dot{\theta_2}\cos\theta_1\cos\theta_2+l_1^2\dot{\theta_2}\cos^2\theta_2)$
$\ =\frac{m_2}{2}
(l_1^2\dot{\theta_1}^2+2l_1l_2\dot{\theta_1}\dot{\theta_2}\cos(\theta_1-\theta_2)+l_1^2\dot{\theta_2}^2)$
$T=T_1+T_2=\frac{m_1+m_2}{2}l_1^2\dot{\theta_1}^2+\frac{m_2}{2}(2l_1l_2\dot{\theta_1}\dot{\theta_2}\cos(\theta_1-\theta_2)+l_1^2\dot{\theta_2}^2)$
位置のエネルギーは
$U_1=-m_1gl_1\cos\theta_1$
$U_2=-m_2g(l_1\cos\theta_1+l_2\cos\theta_2)$
$U=U_1+U_2=-(m_1+m_2)gl_1\cos\theta_1-m_2gl_2\cos\theta_2$
したがって、ラグランジアンは
$L=T-U=\frac{m_1+m_2}{2}l_1^2\dot{\theta_1}^2+\frac{m_2}{2}(2l_1l_2\dot{\theta_1}\dot{\theta_2}\cos(\theta_1-\theta_2)+l_2^2\dot{\theta_2}^2)+(m_1+m_2)gl_1\cos\theta_1+m_2gl_2\cos\theta_2$
オイラー・ラグランジアンの運動方程式を求めるために
$\frac{\partial L}{\partial \theta_1}=-m_2l_1l_2\dot{\theta_1}\dot{\theta_2}\sin(\theta_1-\theta_2)+(m_1+m_2)gl_1\sin\theta_1$
$\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta_1}}=\frac{d}{dt}[(m_1+m_2)l_1^2\dot{\theta_1}+m_2l_1l_2\dot{\theta_2}\cos(\theta_1-\theta_2)]$
$\ = (m_1+m_2)l_1^2\ddot{\theta_1}+m_2l_1l_2\ddot{\theta_2}\cos(\theta_1-\theta_2)$
$\frac{\partial L}{\partial \theta_2}=m_2l_1l_2\dot{\theta_1}\dot{\theta_2}\sin(\theta_1-\theta_2)-m_2gl_2\sin\theta_2$
$\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta_2}}=\frac{d}{dt}[m_2l_1l_2\dot{\theta_1}\cos(\theta_1-\theta_2)+m_2l_2^2\dot{\theta_2})]$
$\ = m_2l_1l_2\ddot{\theta_1}\cos(\theta_1-\theta_2)+m_2l_2^2\ddot{\theta_2}$
$\therefore$
$m_2l_1l_2\dot{\theta_1}\dot{\theta_2}\sin(\theta_1-\theta_2)-(m_1+m_2)gl_1\sin\theta_1 = (m_1+m_2)l_1^2\ddot{\theta_1}+m_2l_1l_2\ddot{\theta_2}\cos(\theta_1-\theta_2)$
$m_2l_1l_2\dot{\theta_1}\dot{\theta_2}\sin(\theta_1-\theta_2)-m_2gl_2\sin\theta_2= m_2l_1l_2\ddot{\theta_1}\cos(\theta_1-\theta_2)-m_2l_2^2\ddot{\theta_2}$
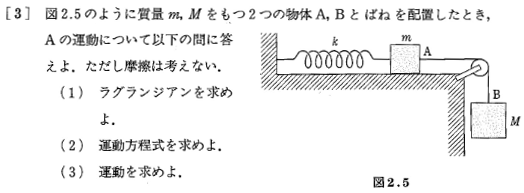
演習問題 p.20-21
(1)
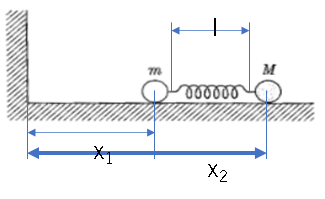
物体Aにかかる力$(kx)$であるので位置のエネルギー$U=-kx^2$、運動エネルギー$T=\frac{1}{2}m\dot{x}^2$
物体Bにかかる力$kmg$,$U=Mgx$、運動エネルギー$T=\frac{1}{2}M\dot{x}^2$
したがって、
$L=\frac{1}{2}(m+M)\dot{x}^2-\frac{1}{2}kx^2+Mgx$
つぎに
$ \frac{\partial L}{\partial \dot{x}}=(m+M)\dot{x}$
$ \frac{d}{dt}\frac{\partial L}{\partial \dot{x}}=(m+M)\dot{x}$
$ \frac{\partial L}{\partial x}=-kx+Mg$
よりラグランジアンの運動方程式は
$((m+M)\ddot{x}=-kx+Mg$ or $(m+M)\ddot{x_1}=kx_1$ (1)
ここで$x_1=-x+Mg/k$
(1)式の一般解は$A \sin(\omega t+\alpha)$であるので
$x_1=A \sin(\omega t + \alpha)$ (2)
$\dot{x_1}=\omega A \cos(\omega t + \alpha)$ (3)
$t=0$とすると
$x=0$、よって$x_1=-Mg/k$,
$\dot{x}=0$, よって$\dot{x_1}=0$
$x_1(0)=A \sin(\alpha)=-Mg/k$
$\dot{x_1(0)}=\omega A \cos( \alpha)=0$
$\omega A \cos(\alpha)=0であるためには \cos(\alpha)=0$
$\therefore$ $\alpha=90^o$
$x_1(0)=A\sin(90^O)=A=-\frac{Mg}{k}$,
$\therefore$ $A=-Mg/k$
$\frac{\partial x_1}{\partial t} = -\omega \frac{Mg}{k} \cos(\omega t + \alpha)$
$x_1=-\frac{Mg}{k} \sin(\omega t+90^o)$
$\frac{\partial x_1}{\partial t} = -\omega \frac{Mg}{k} \cos(\omega t + \alpha)$
$\frac{\partial \dot{x_1}}{\partial t^2} = -\omega^2 \frac{Mg}{k} \sin(\omega t + \alpha)=x_1\omega^2$
$\ddot{x_1}=-x_1 \omega^2$
よって(1)より
$-\omega^2(m+M)x_1=-kx_1$
$\omega=\sqrt{\frac{k}{m+M}}$
$x=\frac{M}{k}g(1-\cos\sqrt{\frac{k}{m+M}}t)$
相対座標では
質点に作用する力は
$F=-kdx=k(l-x_2-x_1)$
ポテンシャルエネルギーは
$U=\frac{1}{2}k(l-x_2-x_1)^2$
運動エネルギーは
$T=\frac{1}{2}m\dot{x_1}^2+\frac{1}{2}M\dot{x_2}^2$
$U=\frac{1}{2}k((l-x)^2$
となる。したがって、
$L=T-U=\frac{1}{2}m\dot{x_1}^2+\frac{1}{2}M\dot{x_2}^2-\frac{1}{2}k((l-x)^2$
重心座標では
$X=\frac{mx_1+Mx_2}{m+M}$を重心座標とし, $x=x_2-x_1$, $\dot{X}=\frac{m\dot{x_1}+M\dot{x_2}}{m+M}$ とすると
$\dot{X}^2=\frac{m^2\dot{x_1}^2+2mM\dot{x_1}\dot{x_2}+M^2\dot{x_2}^2}{(m+M)^2}$
となるので
$T=\frac{1}{2}m\dot{x_1}^2+\frac{1}{2}M\dot{x_2}^2$
$\ \ =\frac{1}{2}(m+M)\dot{X}^2+\frac{1}{2}\frac{mM}{m+M}\dot{x}^2$
となる。したがって
$L=\frac{1}{2}(m+M)\dot{X}^2+\frac{1}{2}\frac{mM}{m+M}\dot{x}^2-\frac{1}{2}((l-x_2-x_1)^2$
(2)
ラグランジュの運動方程式は
$\frac{d}{dt}\frac{\partial L}{\partial \dot{x_i}} = \frac{\partial L}{\partial x_i} $
で表されるから
相対座標では
$M\ddot{x_2}=k(l-x)$
重心座標では
$(M+m)\ddot{X}=0$
$\frac{mM}{m+M}\ddot{x}=k(l-x)$
(3)
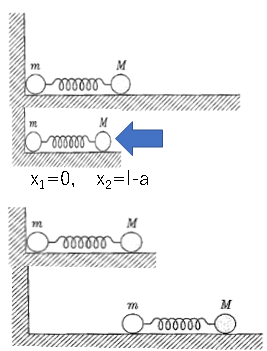
2つの物体を距離$l+a$だけ離すということは$x_2-x_1-l=a$だから$(M+m)\ddot{X}=0$を一回積分すると
$\dot{X}=C$
もう一度積分すると
$X=Ct+D$
したがって、時間の経過にしたがって線形に動く。
また、
$\frac{mM}{m+M}\ddot{x}=-k((l-x)$から$A sin(wt+\alpha)$
$x_3=x-l$とすると$x_3(t)=A sin(wt+\alpha)$
したがって
$\dot{x_3}(t)=-w A cos(wt+\alpha)$
$\ddot{x_3}(t)=-w^2 A sin(wt+\alpha)=-w^2 x_3$
$\frac{mM}{m+M}\ddot{x_3}=\frac{mM}{m+M}(-w^2 x_3)=-kx_3$
したがって、
$w^2=\frac{k(m+M)}{mM} $
ゆえに
$w=\sqrt{\frac{k(m+M)}{mM}} $
$x_3=A sin (wt+\alpha)$
$t=0$のとき
$x_3(0)=A sin (\alpha)=1$ ゆえに $A=a$
$\dot{x_3}(0)=w A cos(\alpha)=0$ ゆえに $\alpha=90^o$
よって
$x_3=A sin (wt+90^o)=a cos(wt)=a cos(\sqrt{\frac{k(m+M)}{mM}}t)$
$\because$
$x=a cos(\sqrt{\frac{k(m+M)}{mM}}t)+l$
質点が壁から離れるまでは
相対座標では
$T=\frac{1}{2}M\dot{x_2}^2 $
$U=\frac{1}{2}l(l-x_2)$
となる。したがって
$L=\frac{1}{2}M\dot{x_2}^2-\frac{1}{2}(l-x_2)$
ラグランジュの運動方程式は
$M\ddot{x_2}=-k(x_2-l)$
$x_3=l-x_3$とすると
$M\ddot{x_3}=kx_3$
したがって、
$x_3(t)=A sin (wt+\alpha)$
$\dot{x_3}(t)=-wA cos (wt+\alpha)$
$\ddot{x_3}(t)=-w^2A sin (wt+\alpha)=-w^2 x_3$
$M \ddot{x_3}=M(-w^2x_3)=-kx_3$
$\because \ w=\sqrt{\frac{k}{M}}$
$t=t_0$のとき
$A sin(w t_0 + \alpha)=a$ then $A=a$ そして $\alpha=\pi/2$
したがって、
$w t_0 +\alpha=\pi \because t_0=\frac{\pi}{2}\sqrt{\frac{M}{k}}$
$t_0$以降では(2)で求めた運動になる。ただし、$t=t-t_0$で置き換える。
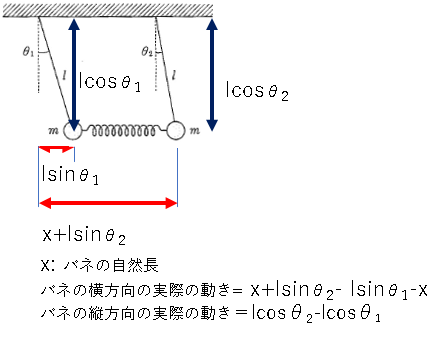
(1)
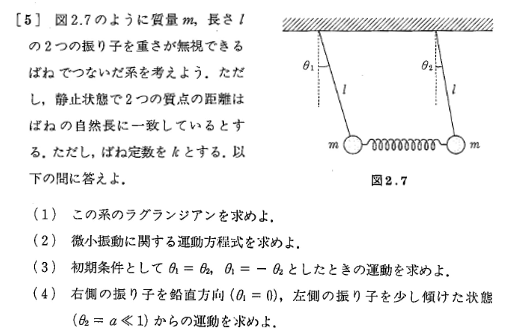
x軸方向の質点の位置:
$x_1=l \cdot sin \theta_1$
$x_2=x+l \cdot sin \theta_2$
y軸方向の質点の位置:
$y_1=l \cdot cos \theta_1$
$y_2=l \cdot cos \theta_2$
したがって、1次の時間微分は
$\dot{x_1}=-l \cdot cos \theta_1 \dot{\theta_1}$
$\dot{x_2}=-l \cdot cos \theta_2 \dot{\theta_2}$
$\dot{y_1}=l \cdot sin \theta_1 \dot{\theta_1}$
$\dot{y_2}=l \cdot sin \theta_2 \dot{\theta_2}$
よって、運動エネルギーは
$ \frac{1}{2}m(\dot{x_1}^2+\dot{x_2}^2+\dot{y_1}^2+\dot{y_2}^2)=$
$ \frac{1}{2}ml^2(\cdot cos^2 \theta_1 \dot{\theta_1}^2+\cdot cos^2 \theta_2 \dot{\theta_2}^2+
\cdot sin^2 \theta_1 \dot{\theta_1}^2+\cdot sin^2 \theta_2^2 \dot{\theta_2}^2)=
\frac{1}{2}ml^2 (\dot{\theta_1}^2+\dot{\theta_2}^2)$
バネのポテンシャルエネルギーは
$U_1=\frac{1}{2}k(x_2-x_1)^2+(y_2-y_1)^2=\frac{1}{2}kl^2[(sin \theta_2-sin \theta_1)^2+(cos \theta_2-cos \theta_1)^2]$
位置のエネルギーは
$U_2=mg(y_1+y_2)=mgl(cos \theta_1+ cos \theta_2)$
したがって、ラグランジアンは
$L=\frac{1}{2}ml^2(\dot{\theta_1}^2+\dot{\theta_2}^2)+mgl(cos \theta_1+ cos \theta_2)-\frac{1}{2}kl^2[(sin \theta_2-sin \theta_1)^2+(cos \theta_2-cos \theta_1)^2]$
(2)
微小振動であるので、$\theta_1<1,\ \theta_2<1, \omega_g^2=g/l, \omega_k^2=k/m$とすると、$sin \theta=\theta$と近似できるから
バネのポテンシャルエネルギーは
$U_1=\frac{1}{2}kl^2(\theta_2-\theta_1)^2$
また、
$\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta_1}}=ml\ddot{\theta_1}$
$\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta_2}}=ml\ddot{\theta_2}$
$\frac{\partial U_1}{\partial \theta_1}=-kl^2(\theta_2-\theta_1)$
$\frac{\partial U_1}{\partial \theta_2}=kl^2(\theta_2-\theta_1)$
$\frac{\partial U_2}{\partial \theta_1}=-mgl sin\theta_1=-mgl\theta_1$
$\frac{\partial U_2}{\partial \theta_1}=-mgl sin \theta_2=-mgl\theta_2$
よって、
$\ddot{\theta_1}=\omega_g^2\theta_1-2\omega_k^2(\theta_2-\theta_1)$
$\ddot{\theta_2}=\omega_g^2\theta_2+2\omega_k^2(\theta_2-\theta_1)$
(3)
初期値が$\theta_1=\theta_2$では2つの質点は同じ方向に動くから上述の式を足し合わせて
$\ddot{\theta_1}+\ddot{\theta_2}=-\omega_g^2(\theta_1+\theta_2)$
よって、角振動数は$\omega=\omega_g$
初期値が$\theta_1=-\theta_2$では2つの質点は逆の方向に動くから上述の式の差は
$\ddot{\theta_1}-\ddot{\theta_2}=-\omega_g^2(\theta_1-\theta_2)-2\omega_k^2(\theta_1-\theta_2)$
よって、角振動数は$\omega=\sqrt{\omega_g^2+2\omega_k^2}$
となる。
(4)
初期値は$\theta_1=0,\ \theta_2=a$であるから、バネの角度の和は$a$を維持するのだから$\theta_1+\theta_2=a$、角度の差は
$\theta_1-\theta_2=-a$を維持する。