一般化線形回帰(GLM)のあてはまりの評価について調べてみた。StatsmodelsのGLMのサマリーレポートには
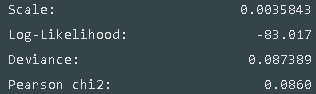
の評価基準が表示される。一般にあてはまり度合いの評価の基準として
- $R_{response}$
- $R_{pearson}$
- $R_{pearson}^2$
- 対数尤度
- 逸脱度(Deviance)
- ナル対数尤度
- ナル逸脱度
がある。statsmodelsではこれらを個別に出力できる。最初にポアソン分布とガンマ分布における対数尤度. 逸脱度(Deviance), ナル対数尤度,ナル逸脱度についてしらべた。つぎにガンマ分布の$R_{response}$, $R_{pearson}$, $R_{pearson}^2$, scaleについて調べた。
- 残差について
線形回帰では、残差(Residual)は、そのモデルの有効性の尺度となる。理想的には残差は標準正規分布にしたがう。しかし、一般化線形モデルは線形回帰モデルよりも一般化されているので、残差が正規分布にしたがうとは限らない。そこで残差を調整してより標準正規分布に近づける。その一連の指標が$R_{response}$、$R_{Pearson}$、$R_{Pearson}^2$、$R_{working}^2$である。$R$はresidualの頭文字である。また、線形モデルの残差と正規分布のような関係をGLMでも実現するために、deviance residualがある。そこでは、2つの基準を導入する。
- フルモデル
1つはすべての観測値を完全に予測できるモデルである。これをフルモデルという。
- ナルモデル
2つ目はすべての観測値を説明変数を使わずに1つの定数のみで予測するモデルで、これをナルモデルという。
残差を扱う場合には観測点に注目している。statsmodelsでもベクトルで計算結果を出力している。
- Deviance(逸脱度)について
$D(\sum d(\theta,y_i))$は観測値と特定のモデルが示す観測値の期待値の差を表現する関数であるが、故意に曖昧にしている。一般化線形回帰では$D$はよく用いられるが、平均からの差の二乗という意味での$D$、despersionの頭文字である。GLMでは、尤度を用いた表現がより有効であり、Deviance residualをGLMでは用いる。$y_i$の記述から個々の観測点に注目していることが分かる。予測モデルの尤度をllf, フルモデルの尤度をllfull,ナルモデルの尤度をllnullとするとDeviance residualとしてはllfull-llf,llf-llnullの2つが考えられる。
Devianceについてはいろいろ混乱を生じる。wikiの英語版には$-2\log(p(y| \hat{\theta}))$をDevianceと呼ぶことは混乱を招くと明記されている。
例:スコットランドの選挙
データは地方税に関する権限を議会に与えるために「はい」と答えた人の割合である。データは32の地区に分割されている。この例の説明変数には1997年4月の調整前地方税額、1998年1月の失業保険総給付額の女性の割合、標準死亡率(UK=100)、労働組合参加率、地域GDP、5から15歳までの子供の割合、女性の失業と地方税の関係が示されている。
観測データ数:32
変数の数:8項目
- YES - 「はい」と答えた人の割合
- COUTAX - 地方税の額
- UNEMPF - 失業保険総給付額の女性の割合
- MOR - 標準化死亡率(UK=100)
- ACT - 労働組合参加率
- GDP - 地域GDP
- AGE - 5から15歳までの子供の割合
- COUTAX_FEMALEUNEMP - 女性の失業と地方税の関係
# pythonの初期化
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy import stats
import statsmodels.api as sm
from statsmodels.graphics.api import abline_plot
データはつぎのように得られる。説明変数には定数を付加した。
sdata = sm.datasets.scotland.load()
y=sdata.endog
x = sm.add_constant(sdata.exog, prepend=False)
ポアソン分布
$p(y|\lambda)=\frac{\lambda^y \exp(-\lambda)}{y!}$
$\lambda$は平均。
mod_p = sm.GLM(y, x, family=sm.families.Poisson())
res_p=mod_p.fit()
print('Log-likelihood',res_p.llf)
print('deviance',res_p.deviance)
print('null Log-likelihood',res_p.llnull)
print('null deviance',res_p.null_deviance)
# Log-likelihood -97.79760284475648
# deviance 5.184605878713687
# null Log-likelihood -111.41003866640344
# null deviance 32.40947752200674
# mu
res_p.mu
# (array([57.69237428, 53.41250292, 50.49148938, 58.10973247, 70.0469828 ,
# 57.07985454, 66.94842531, 66.07693776, 57.91057739, 63.19518335,
# 53.83526675, 61.37282454, 64.50519699, 63.73416138, 60.91929738,
# 74.85772678, 56.83768043, 71.94082256, 64.70321472, 52.1046203 ,
# 64.52124889, 70.72503701, 45.25889961, 54.76898944, 67.07157841,
# 51.87303952, 56.84286865, 58.17583766, 67.36858879, 60.65777469,
# 73.86156189, 69.19970341]),)
# nullmodel
res_p.null
# array([61.440625, 61.440625, 61.440625, 61.440625, 61.440625, 61.440625,
# 61.440625, 61.440625, 61.440625, 61.440625, 61.440625, 61.440625,
# 61.440625, 61.440625, 61.440625, 61.440625, 61.440625, 61.440625,
# 61.440625, 61.440625, 61.440625, 61.440625, 61.440625, 61.440625,
# 61.440625, 61.440625, 61.440625, 61.440625, 61.440625, 61.440625,
# 61.440625, 61.440625])
対数尤度、逸脱度の計算:分布関数の最適化
# full llf
np.sum( stats.poisson.logpmf(np.round(y), mu=np.round(y)))
# -95.21215984845625
# llf
np.sum( stats.poisson.logpmf(np.round(y), mu=np.round(res_p.mu)))
# -97.60865263409067
# null llf
np.sum( stats.poisson.logpmf(np.round(y), mu=61))
# -111.52747980817006
# deviance
(np.sum( stats.poisson.logpmf(np.round(y), mu=np.round(y)))
-np.sum( stats.poisson.logpmf(np.round(y), mu=np.round(mup))))*2
# 4.792985571268844
# null deviance
(np.sum( stats.poisson.logpmf(np.round(y), mu=np.round(y)))
-np.sum( stats.poisson.logpmf(np.round(y), mu=61)))*2
# 32.63063991942761
Deviance Function
Deviance Function $=2\sum[ y_i\log y_i/\mu_i)-y_i+\mu_i]$
# deviance
np.sum(y*np.log(y/mu)-y+mu)*2
# 5.198800302723981
# full deviance
np.sum(y*np.log(y/y)-y+y)*2
# 0
# null deviance
np.sum(y*np.log(y/61)-y+61)*2
# 32.51108255751657
ポアソン分についてはllf,deviance,llnull,null_devianceについて、異なる計算方法でも同じような結果が得られた。計算方法はreferenceとGillを参考にしている。
https://www.statsmodels.org/stable/glm.html
https://www.amazon.co.jp/-/en/Jefferson-M-Gill/dp/1506387349/ref=pd_rhf_gw_p_img_10?_encoding=UTF8&psc=1&refRID=Q7M7A9N13N96G79YY632
ガンマ分布
ガンマ分布の確率密度関数は。
$f(y|\alpha,\beta)=\frac{1}{\Gamma (\alpha)}\beta^\alpha y^{\alpha-1}e^{-\beta y}$
である。$\Gamma$はガンマ関数、$\alpha$は形状パラメータ、$\beta$はスケールパラメータの逆数。
これを$\alpha=\delta, \beta=\delta/\mu$と置き換えると
$f(y|\mu,\delta)=\frac{\delta}{\mu}^\delta\frac{1}{\Gamma (\delta)}y^{\delta-1} e^{-\delta y/\mu}$
となる。また、
$E(Y)=\mu=\frac{\alpha}{\beta}$
$Var(Y)=\frac{\mu^2}{\delta}=\frac{\alpha}{\beta^2}$
となる。
sglm_g = sm.GLM(y, x, family=sm.families.Gamma(sm.families.links.log()))
sglm_res=sglm_g.fit()
print('Log-likelihood',sglm_res.llf)
print('deviance',sglm_res.deviance)
print('null Log-likelihood',sglm_res.llnull)
print('null deviance',sglm_res.null_deviance)
# Log-likelihood -83.10956972527515
# deviance 0.08798781836110652
# null Log-likelihood -145.47042949378488
# null deviance 0.5360720799622841
mu=sglm_res.mu,
mu#=fittedvalues
# (array([57.58367166, 53.32164997, 50.85970407, 58.18727852, 69.75786101,
# 57.05331759, 66.93528354, 65.86630038, 57.72219974, 63.0464292 ,
# 53.62114062, 61.38437904, 64.28556531, 63.77579653, 60.76619906,
# 75.19549011, 56.87375799, 72.2290011 , 64.72845937, 52.3224542 ,
# 64.43493249, 70.7152807 , 45.51861176, 54.69328195, 67.14509988,
# 51.80427267, 56.9071102 , 58.06763807, 67.46066392, 60.58634889,
# 73.95675782, 69.28090911]),)
# nullmodel
null=sglm_res.null
null
# array([61.440625, 61.440625, 61.440625, 61.440625, 61.440625, 61.440625,
# 61.440625, 61.440625, 61.440625, 61.440625, 61.440625, 61.440625,
# 61.440625, 61.440625, 61.440625, 61.440625, 61.440625, 61.440625,
# 61.440625, 61.440625, 61.440625, 61.440625, 61.440625, 61.440625,
# 61.440625, 61.440625, 61.440625, 61.440625, 61.440625, 61.440625,
# 61.440625, 61.440625])
対数尤度の計算:分布関数の最適化
最適化の際に制限を設定してその違いをみた。
params_g = stats.gamma.fit(y)
print(params_g)
lly_g = np.sum( stats.gamma.logpdf(y, params_g[0], loc=params_g[1], scale=params_g[2]) )
lly_g
# (523.0459857901084, -118.7457261830617, 0.3444594530187898)
# -111.38971922872636
params_g = stats.gamma.fit(y,floc=0)
print(params_g)
lly_g = np.sum( stats.gamma.logpdf(y, params_g[0], loc=params_g[1], scale=params_g[2]) )
lly_g
# (59.85966438870558, 0, 1.026411117192844)
# -111.53332667513942
params_g = stats.gamma.fit(y,fa=1,floc=0)
print(params_g)
llnull = np.sum( stats.gamma.logpdf(y, params_g[0], loc=params_g[1], scale=params_g[2]) )
llnull
# (1, 0, 61.440625)
# -163.77828036203903
scale=61.4406625はmuの平均と同じであるのでナルモデルの対数尤度となる。
statsmodelsでは直接$\alpha$と$\beta$が取得できないので、計算してみた。$\alpha=1$と設定されているのが分かる。つまり、2変数のモデルではなく、1変数のモデルとしてガンマ分布を扱っている。
var_mu=sglm_res.model.family.variance(mu)
beta=sglm_res.mu/var_mu
alpha=sglm_res.mu*beta
alpha,beta
# (array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
# 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
# array([0.01736603, 0.01875411, 0.01966193, 0.01718589, 0.0143353 ,
# 0.01752746, 0.0149398 , 0.01518227, 0.01732436, 0.01586133,
# 0.01864936, 0.01629079, 0.01555559, 0.01567993, 0.01645652,
# 0.01329867, 0.0175828 , 0.01384485, 0.01544915, 0.01911225,
# 0.01551953, 0.01414122, 0.02196904, 0.01828378, 0.01489312,
# 0.01930343, 0.0175725 , 0.0172213 , 0.01482345, 0.01650537,
# 0.01352141, 0.01443399]))
np.sum(stats.gamma.logpdf(y,a=alpha,loc=0,scale=1/beta))
# -163.5542382312384
a=1だということがわかったので、loc=0とscale=yとして対数尤度を計算してみた。この場合、scale=y=1/betaとすることで、期待値mu=1/beta=yとなる。これはfull modelに相当するはず。
llfull=np.sum(stats.gamma.logpdf(y,a=1,loc=0,scale=y))
# -163.51024432205784
また、期待値の対数尤度を再度計算してみる。
llmu=np.sum(stats.gamma.logpdf(y,a=1,loc=0,scale=mu))#予測モデル
llmu
# -163.5542382312384
alpha=1,beta=1/muの結果と同じになった。
Deviance Function
Deviance Function$=2\sum [-\log( y_i/\mu_i)*(y_i-\mu_i)/\mu_i]$
Gill 参照
# llf
np.sum(np.log(y/mu)-y/mu-np.log(mu))
# -163.59823214044783
# full model llf
np.sum(np.log(y/y)-y/y-np.log(y))
# -163.51024432205784
# null model llf
np.sum(np.log(1)-1-np.log(sglm_res.null))
# -163.77828036203903
# deviance
np.sum(np.sum(np.log(y/y)-y/y-np.log(y))-np.sum(np.log(y/mu)-y/mu-np.log(mu)))*2
# 0.17597563677998096
近似式ではstatsmodelsの出力するdevianceにはならなかった。そこで
(llfull-llmu)*2
# 0.08798781836111402 (0.08798781836110652)
()内はstatsmodelsのdevianceの出力
# null deviance
2*np.sum(np.log(y/y)-y/y-np.log(y))-2*np.sum(np.log(1)-1-np.log(sglm_res.null))
# 0.5360720799623664
(llfull-llnull)*2
# 0.5360720799623664 (0.5360720799622841)
()内はstatsmodelsのnull devianceの出力
null devianceはほぼ同じ値になった。llf,deviance,llnullの結果を近似計算では再現できなかった。近似式でもとめたDevianceはStatsmodelsのDevianceの2倍になった。
また、stats.gamma.fit(y,fa=1,floc=0)によりモデルを最適化した結果がパラメータが(1, 0, 61.440625)となり対数尤度が-163.77828036203903となった。これはnp.sum(np.log(1)-1-np.log(sglm_res.null))として計算したnull modelのllfと同じである。
a=1,loc=0,scale=yと設定して対数尤度を求めるとnp.sum(np.log(1)-1-np.log(y))として計算したfull modelのllfと同じになる。
確率身度関数を用いた対数尤度からdevianceを計算するとほぼ同じ値となった。
peason chi2 と scale
- peason chi2
$R_{response}=y_i-\mu_i$
$R_{peason}=\sum_{i=1}^n\frac{y_i-\mu_i}{\sqrt{Var{\mu_i}}}=\sum_{i=1}^n(R_{response,i}/\sqrt{Var{\mu_i}})$
$R_{peason}^2=(R_{peason})^2$
- scale
$scale=R_{peason}^2/(degree of freedom of resdiduals)$
print('peason chi2',sglm_res.pearson_chi2)
print('scale',sglm_res.scale)
# peason chi2 0.08622413416317276
# scale 0.0035926722568010924
sdata.endog-mu
# array([[ 2.71632834, -1.02164997, 2.54029593, -1.18727852, -1.05786101,
# -8.25331759, -1.43528354, 4.63369962, 1.37780026, -0.3464292 ,
# -2.02114062, 0.61562096, 4.11443469, 5.42420347, 3.93380094,
# -0.19549011, 5.22624201, -5.0290011 , 2.97154063, 0.3775458 ,
# 1.26506751, 1.4847193 , 1.88138824, -3.39328195, -3.54509988,
# -1.10427267, -5.3071102 , -1.86763807, 0.13933608, -1.68634889,
# 0.74324218, -1.98090911]])
sglm_res.resid_response#=y_i-mu
# array([ 2.71632834, -1.02164997, 2.54029593, -1.18727852, -1.05786101,
# -8.25331759, -1.43528354, 4.63369962, 1.37780026, -0.3464292 ,
# -2.02114062, 0.61562096, 4.11443469, 5.42420347, 3.93380094,
# -0.19549011, 5.22624201, -5.0290011 , 2.97154063, 0.3775458 ,
# 1.26506751, 1.4847193 , 1.88138824, -3.39328195, -3.54509988,
# -1.10427267, -5.3071102 , -1.86763807, 0.13933608, -1.68634889,
# 0.74324218, -1.98090911])
(sglm_res.resid_response/sglm_res.mu)**2
# array([2.22518346e-03, 3.67110744e-04, 2.49471516e-03, 4.16340953e-04,
# 2.29969853e-04, 2.09264379e-02, 4.59796003e-04, 4.94913402e-03,
# 5.69753206e-04, 3.01931207e-05, 1.42076080e-03, 1.00579867e-04,
# 4.09631563e-03, 7.23369448e-03, 4.19083553e-03, 6.75874387e-06,
# 8.44413529e-03, 4.84775031e-03, 2.10752535e-03, 5.20670609e-05,
# 3.85464733e-04, 4.40820895e-04, 1.70835780e-03, 3.84921283e-03,
# 2.78758618e-03, 4.54382389e-04, 8.69727390e-03, 1.03446812e-03,
# 4.26604995e-06, 7.74720944e-04, 1.00996184e-04, 8.17526698e-04])
(sglm_res.resid_pearson)**2
# array([2.22518346e-03, 3.67110744e-04, 2.49471516e-03, 4.16340953e-04,
# 2.29969853e-04, 2.09264379e-02, 4.59796003e-04, 4.94913402e-03,
# 5.69753206e-04, 3.01931207e-05, 1.42076080e-03, 1.00579867e-04,
# 4.09631563e-03, 7.23369448e-03, 4.19083553e-03, 6.75874387e-06,
# 8.44413529e-03, 4.84775031e-03, 2.10752535e-03, 5.20670609e-05,
# 3.85464733e-04, 4.40820895e-04, 1.70835780e-03, 3.84921283e-03,
# 2.78758618e-03, 4.54382389e-04, 8.69727390e-03, 1.03446812e-03,
# 4.26604995e-06, 7.74720944e-04, 1.00996184e-04, 8.17526698e-04])
np.sum((sglm_res.resid_response/sglm_res.mu)**2)
# 0.08622413416317277
# scale
np.sum((sglm_res.resid_response/std_mu)**2)/24
# 0.0035926722567988655
ピアソンのカイ二乗とscaleに関してはStatsmodelsの結果と合成して計算した結果は同じものになった。