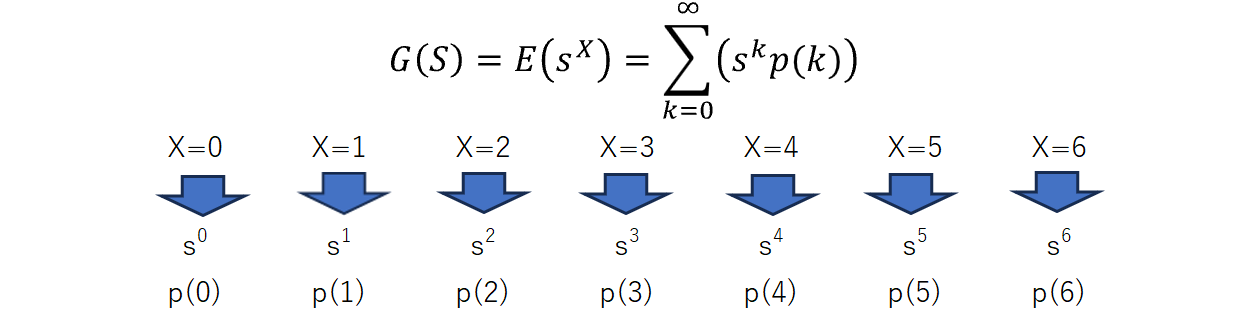ワークブックの２章ではモーメント母関数は$m(\theta)$で記されていて、６章では$M(t)$で書かれていて、混乱しましたが、６章にしたがいました。ChatGPTを検索と論理展開の検証、そしてプログラミングに使っています。
関連するsympyのシートは
https://github.com/innovation1005/qiita_innovation1005
2403242342 6047
母関数入門
数学史において、数列や級数の性質を調べることは重要なテーマの一つでした。これらの性質を理解し、表現するために様々な方法が開発されてきました。その中でも、漸化式と母関数は特に強力なツールです。フィボナッチ数列は、これらの概念を理解するのに最適な例です。一方、ド・モアブルの業績は、確率論と数理統計学の基礎を築く上で非常に重要です。
フィボナッチ数列と母関数
フィボナッチ数列は、簡単な漸化式 $F_n = F_{n-1} + F_{n-2}$ で定義されますが、この数列から派生する性質は複雑であり、数学の多くの分野で応用が見られます。特に、この数列の成長率が黄金比 $\phi = \frac{1 + \sqrt{5}}{2}$ に収束することは、数学の美しい結果の一つです。この性質は、フィボナッチ数列の母関数 $G(x) = \frac{x}{1 - x - x^2}$ を分析することで導出できます。
ド・モアブルと確率論
アブラハム・ド・モアブルは、二項分布が正規分布に近似されることを示しました。これは、大数の法則と中心極限定理への道を開いた重要な発見です。ド・モアブルは、二項定理を用いて、成功確率 $p$ の独立試行を $n$ 回行ったときの成功回数の分布が、$n$ が十分大きい場合に正規分布に近似されることを示しました。これは、多くの独立な試行の結果の合計が、特定の条件下で、予測可能な形（正規分布）を取ることを意味し、二項分布の平均 $\mu = np$ と分散 $\sigma^2 = np(1-p)$ を用いて、確率変数が正規分布 $\mathcal{N}(\mu, \sigma^2)$ に従うことを示します。ド・モアブル＝ラプラスの極限定理の背後にある数学的洞察は、二項分布の確率質量関数に含まれる二項係数が、$n$ が増加するにつれて正規分布の確率密度関数の形状に近づくということです。この現象は、冪級数の展開と極限の概念を通じて数学的に理解され、統計学におけるサンプリング理論の基礎を形成しています。母関数はここでも重要な役割を果たし、確率変数の特性は確率分布よりも母関数の方が正確であるとまで言及されることもあります。
漸化式、母関数、確率論の交差点
これらの話題は、数学的な対象の動態を理解するために開発された異なる手法が、互いにどのように関連しているかを示しています。漸化式は数列や級数の局所的な関係を捉えるために用いられ、母関数はそれらの全体的な性質を解析するためのツールです。また、母関数は、確率論における基本的な分布の理解に貢献し、統計学の発展に繋がりました。
数学的概念の相互作用
-
漸化式は、数列の各項が前の項に依存する方法を定義します。これにより、数列の具体的な挙動やパターンを理解することができます。フィボナッチ数列のように、簡潔な漸化式から出発しても、その振る舞いは非常に複雑で興味深い性質を示すことがあります。
-
母関数は、数列全体を一つの関数に統合することで、数列の性質をより広い視点から分析します。これにより、数列の一般項を見つける、収束性を調べる、またはより複雑な関係性を解明することができます。
-
確率論では、現実世界の不確実性をモデル化し、特定の出来事の発生確率を推定します。ド・モアブルの二項分布の研究は、確率論における基礎的な理論の一つとなり、後の研究者たちがさらに発展させていきました。
-
組み合わせ数学: 組み合わせ問題における対象の数え上げや、特定の性質を持つ組み合わせの数を求める際に有効です。
-
整数論: 整数の分割数や素数定理の証明においても、母関数（特にディリクレ母関数）が重要な役割を果たします。
確率母関数
確率母関数$G(s)$は、確率変数の分布の性質を表現する手法の一つで、離散確率変数$X$が取りうる各値$k$に対して、その確率を$p(k)$としたとき、次のように定義されます：
$$G(s) =E(s^X)= \sum_{k=0}^\infty(s^kp(k))=s^0p(0) + s^1p(1) + s^2p(2)+ s^3p(3) + ...---(1)$$
$\Sigma$は無限和を意味し、$k$ は通常0から始まります。確率母関数は、確率変数が取る各値 $k$ に対する確率 $p(k)$ と、それに対応する形式的な変数 $s$ の $k$ 乗項 ($s^X$) を組み合わせて定義されます。
定義から分かるように、この式は確率変数 $X$ の期待値 $E(s^X)$ そのものです。$G(s)$ は多項式または級数となることもあります。たとえば、$s=1$のとき上式は
$$G(1)=1^0p(0)+1^1p(1) + 1^2p(2) + 1^3p(3) + ...=p(0)+p(1)+p(2)+p(3)+...$$
です。
from sympy import symbols, Sum, oo
k, s = symbols('k s')
p = symbols('p') # シンボルとしての確率
G = Sum(p * s**k, (k, 0, oo)) # 確率母関数の定義
print("確率母関数(s = 1):")
display(G.subs(s, 1))
式(1)が表現できています。
解析的な分析
確率母関数がどのように確率関数の性質を表現してくれるのでしょうか。確率母関数は、各値 $k$ に対する確率 $p(k)$ を $s$ のべき級数とすることで、確率変数の確率分布に関する情報を表現しています。
母関数の基本的な振る舞い
異なる $s$ 値における確率母関数の振る舞いを観察します。
ベルヌーイ分布
ベルヌーイ分布を例に見ていきます。ベルヌーイ確率変数 $X$ の確率関数は以下のようになります。
$X = 0$ のとき(失敗確率)：$q=1 - p$
$X = 1$ のとき(成功確率)：$p$
確率母関数 $G(s)$ は、これらの確率質量を $s$ の各乗数で重み付けした和として定義されます。
$$G(s) = E(s^X)= \sum_{k=0,1}(s^kp(k))=qs^0 + ps^1= q + ps$$
この式を解析的に分析することで、異なる $s$ 値における確率母関数の振る舞いを観察できます。例として、いくつかの $s$ 値に対する確率母関数の値を計算してみましょう：
$s=0$ の場合：$G(0)=p+q⋅0=p$
この結果から、確率母関数 $G(s)$ は $s=0$ のとき、成功確率 $p$ に等しいことがわかります。
$s=1$ の場合：$G(1)=p+q⋅1=p+q=1$
この結果から、確率母関数 $G(s)$ は $s=1$ のとき、確率の合計が1になることがわかります。
$s=-1$ の場合：$G(−1)=p+q⋅(−1)=p−q$
この結果から、確率母関数 $G(s)$ は $s=-1$ のとき、成功確率と失敗確率の差に等しいことがわかります。これにより、ベルヌーイ分布の確率母関数を解析的に計算し、異なる $s$ 値における振る舞いを理解することができます。
確率母関数の便利な役割
確率母関数は、
- 変数の変換と合成分布の解析、
- 期待値と分散の導出、
- 異なる性質の解析、
- 漸近理論への応用で重要な役割を果たします。
独立な確率変数の和や積の確率母関数を簡単に求めることができます。また、確率変数のモーメント（期待値、分散など）を確率母関数を微分することで効率的に計算できます。
分数と合成関数の微分
このような分析を実行するためには分数の微分と合成関数の微分の基礎知識が必要です。
- 分数の微分(商の法則)
分数の微分は、分子と分母それぞれを微分し、それを元にして導関数を求める操作です。一般的な分数 $y= \frac{f(x)}{g(x)}$の微分は以下のようになります。
分子関数$f(x)$ および分母関数$g(x)$ を用意します。
分子関数$f(x)$を$x$で微分し、導関数$f'(x)$ を求めます。
分母関数$g(x)$を$x$で微分し、導関数$g'(x)$ を求めます。
導関数$f'(x)$および $g'(x)$を用いて、分数の導関数 $y'$を計算します。
$$y'=\frac{f'(x)⋅g(x)−f(x)⋅g'(x)}{(g(x))^2}$$
この手順に従って、与えられた分数の導関数を計算できます。分子と分母それぞれを微分し、その結果を用いて導関数を求めることになります。
- 合成関数の微分(チェーンルール)
合成関数の微分は、外側の関数$f(u)$ と内部の関数$u=g(x)$ に対して以下のように計算されます。
$$\frac{d}{dx}[g(h(x))]=g'(h(x))⋅h'(x)$$
ここで、$g'(h(x))$ は外側の関数$g(u)$を $u=h(x)$ で微分したものであり、$h'(x)$ は内部の関数 $h(x)$ を $x$ で微分したものです。
期待値と分散
期待値、分散などを効率的に計算できます。例えば、$G(s)$ の1階微分を $s=1$ で評価することで、確率変数の期待値（平均）を求めることができます。
$G(s) = E[s^X]$を$s$に関して一階微分することを考えます。ここで、$X$は離散確率変数であると仮定し、$p(x)$を$X$が特定の値$x$を取る確率とします。このとき、$G(s)$は以下のように書き表されます：
$$G(s) = E[s^X] = \sum_{x} s^x p(x)$$
この式を$s$に関して微分します。微分の操作は和の中に入れることができるので、各項を$s$に関して微分すると、次のようになります：
$$\frac{dG(s)}{ds} = \sum_{x} \frac{d}{ds}(s^x) p(x)$$
ここで、$s^x$の$s$に関する微分は$x \cdot s^{x-1}$です。したがって、
$$\frac{dG(s)}{ds} = \sum_{x} x \cdot s^{x-1} p(x)$$
これに$s=1$を代入すると$E(X)$となります。
$$E(X)=\frac{dG(s)}{ds}|_{s=1}$$
同様に、2階微分を用いると分散を求めることができます。
2階微分は
$$\frac{d^2G(s)}{ds^2} = \sum_{x} x(x-1) \cdot s^{x-2} p(x)$$
となり、これに$s=1$を代入すると、
$$\frac{d^2G(s)}{ds^2}|{s=1} = \sum{x} x(x-1) \cdot p(x) =E[X(X-1)] $$
が得られます。したがって、
$$E[X^2] = E[X(X-1)] + E[X]$$
となります。最終的に、
$$Var(X) = E[X^2] - [E(X)]^2=\frac{d^2G(s)}{ds^2}|_{s=1}+E(X)-[E(X)]^2$$
を使用して分散を求めることができます。
ベルヌーイ分布
ベルヌーイ確率変数 $X$ の確率母関数 $G(s)$ は、
$G(s) = (1 - p)s^0 + ps^1= 1 - p + ps$
となります。
$G(s) = (1 - p)s^0 + ps^1$ の1階微分を求めるには、各項に関して微分を行います。$1 - p$ は定数項なので、その微分は0です。$ps^1$ の微分は $p$ です。これらを合計すると、1階微分 $dG/ds$ は $p$ になります。$G'(s)=E(X)=p$
$G(s) = (1 - p)s^0 + ps^1$ の2階微分を求めるには、1階微分に対してさらに微分を行います。1階微分 $dG/ds$ は $p$ ですが、これは定数です。定数の微分は0になるので、2階微分 $d^2G/ds^2$ は 0 になります。$G"(s)=E(X(X-1)=0$、よって、$Var(X)=E(X^2)-E(X)+E(X)-[E(X)]^2=0+p-p^2=p(1-p)$
import sympy as sp
# 変数と確率変数を定義
s, p = symbols('s p')
k_values = [0, 1] # ベルヌーイ分布の取りうる値
# ベルヌーイ分布の確率母関数
G =(1-p) * s**k_values[0] + p * s**k_values[1]
print("確率母関数 G(s):",G)
#1階の微分
dG= G.diff(s,1)
display("1階の微分 :",dG)
dG2= G.diff(s,2)
display("2階の微分 :",dG2)
display("期待値 E[X] :", dG.subs(s, 1))
display('分散 Var[X] :', sp.simplify(dG2.subs(s, 1)+dG.subs(s, 1) - dG.subs(s, 1)**2))
幾何分布
幾何分布の確率関数は以下のようになります：
$$P(X=k)=(1−p)^{k−1}p$$
ここで、$X$は幾何分布に従う確率変数、$k$は初めて成功するまでの試行回数（非負整数）、$p$は成功確率です。この分布は、最初の成功が得られるまでの試行回数がどれだけかを表現します。
幾何分布の確率母関数は次のように表されます：
$$G(s)=E(s^X)=\sum_{k=1}^\infty s^k(1−p)^{k−1}p=\frac{p}{1−(1−p)s}$$
$G(s) = \frac{p}{1−(1−p)s}$ の1階微分を求めるには、分数の微分を使います。
まず$f(s)=p$と$g(s)=1−(1−p)s$とすると
$y'=\frac{f'(s)⋅g(s)−f(s)⋅g'(s)}{(g(s))^2}$になります。
$f'(s)=0$,$g'(s)=-p+1$より、$y'=\frac{p(1-p)}{[1−(1−p)s]^2}$
$G(s) = \frac{p}{1−(1−p)s}$ の2階微分を求めるには、分数の微分と合成関数の微分を用います。
$f_2(s)=p(1-p)$
$g_2(s)=[1−(1−p)s]^2$とすると
$f_2'(s)=0$,$g_2'(s)=2(1-p)[1-(1-p)s]$より、
$y"=\frac{0\cdot f_2(s)-⋅f(s)g_2'(s)=$
$\frac{0-p(1-p)2(1−(1−p)s)(1-p)}{g_2(s)^2}=$
$\frac{(1−(1−p)s)2p(1-p)^2}{[1−(1−p)s]^4}=$
$\frac{2p(1-p)^2}{(1−(1−p)s)^3}$
p = symbols('p', real=True, positive=True) # 成功確率
# 幾何分布の確率母関数の定義
G = Sum(p * (1 - p)**k * s**k, (k, 0, oo))
G = p/(1-(1-p)*s)
#1階の微分
dG= sp.simplify(G.diff(s,1))
display("1階の微分 :",dG)
dG2= sp.simplify(G.diff(s,2))
display("2階の微分 :",dG2)
# 期待値 E[X]
E_X = dG.subs(s, 1)
display("期待値 E[X] :", E_X)
display('分散 Var[X] :', sp.simplify(dG2.subs(s, 1)+E_X - E_X**2))
二項分布
2項分布（二項分布）の確率関数は以下のように表現されます：
確率関数：
$$P(X = k) = \binom{n}{k} p^k (1 - p)^{n - k} $$
ここで、$n$ は試行回数、$k$ は成功回数、$p$ は1回の試行で成功する確率です。また、$\binom{n}{k}$ は二項係数を表します。
確率関数から確率母関数を得る式変形の過程を示します。
$G(s) = \sum_{k=0}^\infty s^k P(k) = \sum_{k=0}^\infty s^k \binom{n}{k} p^k (1 - p)^{n - k}= \sum_{k=0}^\infty \binom{n}{k} (ps)^k (1 - p)^{n - k}=\binom{n}{0} (ps)^0 (1 - p)^{n - 0} + \binom{n}{1} (ps)^1 (1 - p)^{n - 1} + \binom{n}{2} (ps)^2 (1 - p)^{n - 2} + \ldots $
これは2項定理により$[(ps) + (1 - p)]^n$を展開すると得られます：
$[(ps) + (1 - p)]^n = \binom{n}{0} (ps)^0 (1 - p)^{n - 0} + \binom{n}{1} (ps)^1 (1 - p)^{n - 1} + \binom{n}{2} (ps)^2 (1 - p)^{n - 2} + \ldots$
したがって、上記の展開は実際には確率母関数 $G(s)$ の式そのものです。このように、指数関数のべき乗の和の形を利用することで、確率母関数 $G(s)$ の式を簡略化できます。
$ G(s) = (ps + 1 - p)^n $
これが2項分布の確率母関数です。
この形に基づいて、期待値 $E[X]$ および分散 $\text{Var}[X]$ を求めてみましょう。
まず、期待値 $E[X]$ です。確率母関数の一階微分を $s = 1$ で評価します：
$$E[X] = \frac{dG}{ds} \bigg|{s=1} = n(ps + (1-p))^{n-1} \cdot p \bigg|{s=1} = np $$
次に、分散 $\text{Var}[X]$ を求めます。確率母関数の二階微分を $s = 1$ で評価します：
$$E[X(X-1)] = \frac{d^2G}{ds^2} \bigg|{s=1} = n(n-1)(ps + (1-p))^{n-2} \cdot p \bigg|{s=1} = n(n-1)p^2 $$
そして、分散は以下のように計算されます：
$$\text{Var}[X] = E[X^2] - (E[X])^2 = n(n-1)p^2 + np - (np)^2 = np(1-p)$$
from sympy import symbols, diff
# 変数とパラメータの定義
n, k, p, s = symbols('n k p s')
# 確率母関数の定義
G = (p*s + (1-p))**n
# 期待値の計算
E_X = diff(G, s).subs(s, 1) # 一階微分をs=1で評価
E_X_squared = diff(G, s, 2).subs(s, 1) # 二階微分をs=1で評価
Var_X = E_X_squared +E_X- E_X**2
# 結果の表示
display("期待値 E[X]:", E_X)
display("分散 Var[X]:", sp.simplify(Var_X))
ポアソン分布
ポアソン分布の確率関数は以下のように表されます：
$$P(X = k) = \frac{e^{-\lambda} \lambda^k}{k!}$$
ここで、$X$ は事象の数、$k$ は具体的な事象の数、$\lambda$ は平均発生回数です。確率関数は、ある特定の期間や空間内での事象の数が $k$ 回となる確率を表しています。
確率母関数を求める過程は以下の通りです。
まず、確率母関数 $G(s)$ の定義に基づいて確率関数をべき級数で表現します：
$$G(s) = \sum_{k=0}^\infty s^k P(k) = \sum_{k=0}^\infty s^k \frac{e^{-\lambda} \lambda^k}{k!}$$
この式は指数関数とべき乗の和であるため、指数関数の級数展開を利用して簡略化します。指数関数の級数展開は次のようになります：
$$e^x = \sum_{k=0}^\infty \frac{x^k}{k!}$$
したがって、確率母関数 $G(s)$ は次のようになります：
$$G(s) = \sum_{k=0}^\infty \frac{(s\lambda)^k e^{-\lambda}}{k!} = e^{-\lambda} \sum_{k=0}^\infty \frac{(s\lambda)^k}{k!} = e^{\lambda(s-1)}$$
確率母関数から平均を求めるには、確率母関数を $s=1$ で微分します。
平均 $E[X]$ の計算:
E[X] = \frac{dG}{ds} \bigg|_{s=1} = \frac{d}{ds} e^{\lambda(s-1)} \bigg|_{s=1} = \lambda e^{\lambda(1-1)} = \lambda
次に、確率母関数から分散を求めるためには、確率母関数の二階微分を $s=1$ で計算します。
分散 $\text{Var}[X]$ の計算:
E[X(X-1)] = \frac{d^2G}{ds^2} \bigg|_{s=1} = \frac{d^2}{ds^2} e^{\lambda(s-1)} \bigg|_{s=1} = \lambda^2 e^{\lambda(1-1)} = \lambda^2
そして、分散は以下のように計算されます：
$$\text{Var}[X] = E[X(X-1)] +E[X]- (E[X])^2 = \lambda^2+\lambda - \lambda^2 = \lambda$$
したがって、ポアソン分布の平均は $\lambda$ であり、分散も $\lambda$ です。
from sympy import symbols, Sum, exp, factorial
# 変数とパラメータの定義
k, s, λ = symbols('k s λ')
# ポアソン分布の確率関数
P_X = exp(-λ) * λ**k / factorial(k)
# 確率母関数の定義と計算
G = Sum(s**k * P_X, (k, 0, oo))
G = G.doit()
# 確率母関数の表示
display("母関数:",sp.simplify(G))
# 平均の計算
E_X = diff(G, s).subs(s, 1)
# 分散の計算
Var_X = diff(G, s, 2).subs(s, 1) + E_X - E_X**2
# 結果の表示
display("平均 E[X]:", E_X)
display("分散 Var[X]:", Var_X)
モーメント母関数(積率母関数)
モーメント母関数は、確率変数の分布を特徴付けるもう一つの重要な数学的手法です。確率変数の分布の特性を、その確率変数のべき乗の期待値の列（モーメント）として捉えます。モーメント母関数 $M(t)$ は、次のように定義されます：
$$M(t) = E[e^{tx}]$$
ここで、$E$ は期待値を意味し、$x$ は確率変数を示します。パラメータ $t$ は任意の実数です。
例えば、$M(t)$ を $t$ のべき級数として展開すると、次のようになります：
$$M(t) = E[e^{tx}] = 1 + tE[x] + \frac{t^2}{2!}E[x^2] + \frac{t^3}{3!}E[x^3] + \ldots$$
この展開から、$E[x]$ は一次モーメント（平均）、$E[x^2]$ は二次モーメント（分散）、$E[x^3]$ は三次モーメント（歪度）といった形でモーメントを求めることができます。
モーメント母関数（MGF）は非常に強力な数学的手法であり、確率変数や確率分布の多くの特性を網羅的に理解するための鍵です。特に以下のような点でその有用性が際立っています。
- 簡便性
- 和の分布
- 定理としての利用
- 分布の同一性の判定
- 多変量分布
そのため、モーメント母関数は確率論や統計学、さらには金融工学、信号処理、機械学習といった多くの応用分野で広く用いられています。
モーメント母関数は一般的に確率変数のすべてのモーメントを捉えることができますが、すべての確率分布に対してモーメント母関数が存在するわけではありません。確率変数の分布が無限に発散する場合や、特定の領域で定義されない場合などには適用できません。
モーメント母関数は、特に以下のような分布に対してよく使われます：
- 正規分布（ガウス分布）
- 指数分布
- ポアソン分布
- ガンマ分布
- ベータ分布
これ以外にも、多くの確率分布においてモーメント母関数が有用な情報を提供します。
モーメント母関数の導出
正規分布
正規分布の確率密度関数（pdf）は
$$
f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
$$
と定義されます。モーメント母関数 $M(t)$ は次のように定義されます。
$$
\begin{aligned}
M(t) &= E[e^{tx}] = \int_{-\infty}^{\infty} e^{tx} f(x) , dx = \int_{-\infty}^{\infty} e^{tx} \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx\
&= \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{1}{2\sigma^2} (x^2 - 2\mu x + \mu^2) + tx} , dx
\end{aligned}
$$
指数部分を整理し、完全平方にすると、
$$
\begin{aligned}
M(t) &= \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{1}{2\sigma^2}[x - (\mu + \sigma^2 t)]^2 + \mu t + \sigma^2 t^2}, dx\
&= \frac{1}{\sqrt{2\pi}\sigma} e^{\mu t + \frac{\sigma^2 t^2}{2}} \int_{-\infty}^{\infty} e^{-\frac{1}{2\sigma^2} [(x - \mu - \sigma^2 t)^2]} , dx
\end{aligned}
$$
ここで正規分布の確率密度関数の積分が1である、という性質と一般的なガウス積分$\int_{-\infty}^{\infty} e^{-ax^2} , dx = \sqrt{\frac{\pi}{a}} ( a > 0 )$から
$
\int_{-\infty}^{\infty} e^{-\frac{1}{2\sigma^2} ((x - \mu - \sigma^2 t)^2)} , dx = \sqrt{2\pi} \sigma
$の値を代入すると、モーメント母関数 $M(t)$ は次のようになります。
$$
M(t) = e^{\mu t + \frac{1}{2}\sigma^2 t^2}
$$
指数分布
指数分布の確率関数は以下のように表されます：
$$f(x) = \lambda e^{-\lambda x}$$
ここで、$x$ は確率変数の値、$\lambda$ は正の定数です。
指数分布のモーメント母関数を導出するために、確率関数からモーメント母関数の定義を用いて計算します。
$$M(t) = E[e^{tx}]= \int_{0}^{\infty} e^{tx} \lambda e^{-\lambda x} dx= \lambda \int_{0}^{\infty} e^{(t - \lambda) x} dx = \frac{\lambda}{t - \lambda} \left[e^{(t - \lambda) x}\right]_{0}^{\infty}$$
上限が無限大のため、指数関数が0に収束することから次のようになります：
$$M(t) = \frac{\lambda}{t-\lambda} \cdot 0 - \frac{\lambda}{t - \lambda} \cdot (-1) = \frac{\lambda}{t-\lambda}$$
注意点としてこのモーメント母関数が $(t < \lambda)$ のときにのみ存在します。
ポアソン分布
ポアソン分布の確率関数は以下のように表されます：
$$P(X = k) = \frac{e^{-\lambda} \lambda^k}{k!}$$
モーメント母関数は次のように定義されます：
$$M_X(t) = E[e^{tx}] = \sum_{k=0}^\infty e^{tk} \cdot \frac{e^{-\lambda} \lambda^k}{k!} = \sum_{k=0}^\infty \frac{e^{tk} e^{-\lambda} \lambda^k}{k!}
= \sum_{k=0}^\infty \frac{(e^t \lambda)^k}{k!} \cdot e^{-\lambda} = e^{-\lambda} \sum_{k=0}^\infty \frac{(e^t \lambda)^k}{k!}
$$
最後の式は、指数関数のテイラー展開 $(e^x = \sum_{n=0}^\infty \frac{x^n}{n!})$ の形になっています。よって、
$$
M_X(t) = e^{-\lambda} e^{\lambda e^t} = e^{\lambda(e^t - 1)}
$$
と簡約できます。
ガンマ分布
ガンマ分布の確率密度関数（pdf）は以下のように与えられます。
$$
f(x; a, b) = \frac{x^{a-1} e^{-\frac{x}{b}}}{b^a \Gamma(a)}
$$
この分布に対するモーメント母関数（MGF）$ M(t) $は以下のように定義されます。
$$
M(t) = \mathrm{E}[e^{tX}] = \int_{0}^{\infty} e^{tx} f(x; a, b) dx
$$
この式にガンマ分布のpdfを代入すると、
$$
M(t) = \int_{0}^{\infty} e^{tx} \frac{x^{a-1} e^{-\frac{x}{b}}}{b^a \Gamma(a)} dx
$$
ここで、$t < \frac{1}{b}$ のときにのみ積分が収束することに注意が必要です。
ここで、積分の中を整理してみましょう。
$$
\begin{aligned}
M(t) &= \frac{1}{b^a \Gamma(a)} \int_{0}^{\infty} x^{a-1} e^{(t - \frac{1}{b})x} dx \
&= \frac{1}{b^a \Gamma(a)} \int_{0}^{\infty} x^{a-1} e^{-(\frac{1}{b} - t)x} dx
\end{aligned}
$$
この積分は、$ \frac{1}{b} - t > 0 $、つまり $ t < \frac{1}{b} $ のときにのみ成立します。ここで、$u=(1/b-t)x$と置くと、$dx/du=1/(1/b-t)$となります。よって、
$$
\begin{aligned}
\int_{0}^{\infty} x^{a-1} e^{-(\frac{1}{b}-t)x} dx &=
\int_{0}^{\infty} \left(\frac{u}{\frac{1}{b}-t}\right)^{a-1} e^{-u}\left(\frac{1}{\frac{1}{b}-t}\right) du\
&=\left(\frac{b^a}{(1-b t)^a}\right)\int_{0}^{\infty}u^{a-1} e^{-u} du
\end{aligned}
$$
次に、ガンマ関数の定義を用いてこの積分を評価します。ガンマ関数は
$$
\Gamma(a) = \int_{0}^{\infty} x^{a-1} e^{-x} dx
$$
であり、積分の結果に $ \frac{1}{b^a \Gamma(a)} $ を掛け合わせると、
$$
M(t) = \frac{1}{b^a \Gamma(a)} \left(\frac{b^a}{(1-b t)^a}\right)\int_{0}^{\infty}u^{a-1} e^{-u} du =\frac{1}{b^a \Gamma(a)} \left(\frac{b^a}{(1-b t)^a}\right)\Gamma(a) =\left( 1 - b t \right)^{-a}
$$
となります（但し、$ t < \frac{1}{b} $）。このように、ガンマ分布のモーメント母関数 $ M(t) $ は $ (1 - b t)^{-a} $ であり、その有効範囲は $ t < \frac{1}{b} $ です。
ベータ分布
ベータ分布の確率密度関数（pdf）は次のように定義されます：
$$
f(x; \alpha, \beta) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)}
$$
ここで $ B(\alpha, \beta) $ はベータ関数であり、$ B(\alpha, \beta) = \int_0^1 t^{\alpha-1}(1-t)^{\beta-1} dt $ です。
モーメント母関数 $ M(t) $ は次のように定義されます：
$$
M(t) = \mathrm{E}[e^{tX}] = \int_{0}^{1} e^{tx} f(x) , dx
$$
この式にベータ分布のpdfを代入すると、
$$
M(t) = \int_{0}^{1} e^{tx} \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)} , dx
$$
この積分は一般的な形では解析的に評価することは難しいです。ここで$e^{tx}$についてマクローリング展開をおこなうと
$$M(t)=1+\sum_{k=1}^\infty \left( \Pi_{r=0}^{k-1} \frac{\alpha+r}{\alpha+\beta+r}\right)\frac{t^k}{k!}$$
となります。
利便性
MGFを用いれば、確率変数の各次のモーメント（平均、分散、歪度、尖度など）がMGFの導関数から簡単に得られます。
平均と分散
正規分布
正規分布のモーメント母関数（Moment Generating Function, MGF）は以下のように表されます：
$$
M(t) = e^{\mu t + \frac{1}{2}\sigma^2 t^2}
$$
モーメント母関数を用いて平均（期待値）と分散を求めるには、モーメント母関数を$ t $に関して微分し、その後$ t=0 $を代入します。
- 平均の計算
平均（または一次モーメント、$\mu$)は以下で計算されます：
$$
E[X] = M'(0)
$$
モーメント母関数$ M(t) $を$ t $で一回微分すると：
$$
M'(t) = \mu e^{\mu t + \frac{1}{2}\sigma^2 t^2} + \sigma^2 t e^{\mu t + \frac{1}{2}\sigma^2 t^2}
$$
これを$ t=0 $に代入すると、
$$
M'(0) = \mu e^{\mu \cdot 0 + \frac{1}{2}\sigma^2 \cdot 0} + \sigma^2 \cdot 0 e^{\mu \cdot 0 + \frac{1}{2}\sigma^2 \cdot 0} = \mu
$$
よって、平均（期待値）は$ \mu $です。
- 分散の計算
分散（または二次中心モーメント、$\sigma^2$)は以下で計算されます：
$$
\text{Var}[X] = M''(0) - [M'(0)]^2
$$
モーメント母関数$ M(t) $を$ t $で二回微分すると：
$$
M''(t) = (\mu^2 + \sigma^2) e^{\mu t + \frac{1}{2}\sigma^2 t^2} + 2\mu \sigma^2 t e^{\mu t + \frac{1}{2}\sigma^2 t^2} + \sigma^4 t^2 e^{\mu t + \frac{1}{2}\sigma^2 t^2}
$$
これを$ t=0 $に代入すると、
$$
M''(0) = \mu^2 + \sigma^2
$$
よって、分散は
$$
\text{Var}[X] = (\mu^2 + \sigma^2) - \mu^2 = \sigma^2
$$
指数分布
指数分布の確率密度関数（pdf）は次のように表されます：
$$
f(x;\lambda) = \lambda e^{-\lambda x} \quad (x \geq 0, \lambda > 0)
$$
指数分布のモーメント母関数（Moment Generating Function, MGF）は以下で定義されます：
$ t < \lambda $ のときに収束するため、この条件下で、
$$
M(t) = \frac{\lambda}{\lambda - t}
$$
- 平均（期待値）の計算
平均（または一次モーメント）は、モーメント母関数の $ t $ に関する一次導関数を $ t=0 $ に代入することで得られます：
$$
E[X] = M'(0)
$$
モーメント母関数 $ M(t) $ の一次導関数 $ M'(t) $ は、
$$
M'(t) = \frac{\lambda}{(\lambda - t)^2}
$$
これを $ t=0 $ に代入すると、
$$
M'(0) = \frac{\lambda}{\lambda^2} = \frac{1}{\lambda}
$$
よって、平均（期待値）は $ \frac{1}{\lambda} $ です。
- 分散の計算
分散は、モーメント母関数の $ t $ に関する二次導関数を $ t=0 $ に代入して、平均の二乗を引くことで得られます：
$$
\text{Var}[X] = M''(0) - (M'(0))^2
$$
$ M(t) $ の二次導関数 $ M''(t) $ は、
$$
M''(t) = \frac{2\lambda}{(\lambda - t)^3}
$$
これを $ t=0 $ に代入すると、
$$
M''(0) = \frac{2\lambda}{\lambda^3} = \frac{2}{\lambda^2}
$$
よって、分散は
$$
\text{Var}[X] = \frac{2}{\lambda^2} - \left(\frac{1}{\lambda}\right)^2 = \frac{1}{\lambda^2}
$$
以上から、指数分布の平均は $ \frac{1}{\lambda} $、分散は $ \frac{1}{\lambda^2} $ となります。モーメント母関数からこれらの値を求めることができました。
ガンマ分布
この確率分布のモーメント母関数（MGF）は以下のように求められます：
$$
M(t) = \frac{1}{b^a \Gamma(a)} \Gamma(a, 1/b - t) b^a = (1 - b t)^{-a}
$$
- 平均（期待値）の計算
平均は、モーメント母関数 $ M(t) $ の $ t $ に関する一次導関数を $ t = 0 $ に代入して求めます：
$$
E[X] = M'(0)
$$
$M'(t)$ を求めると、
$$
M'(t) = -a(1 - b t)^{-a-1}(-b) = ab (1 - b t)^{-a-1}
$$
この値を $ t = 0 $ に代入すると、
$$
E[X] = M'(0) = ab (1 - 0)^{-a-1} = ab
$$
- 分散の計算
分散は、$ M''(0) - (M'(0))^2 $ で求められます。先ず $ M''(t) $ を求めます：
$$
M''(t) = -a(-a-1)(-b)^2 (1 - b t)^{-a-2}=a(a+1)b^2(1-bt)-{-a-2}
$$
この値を $ t = 0 $ に代入すると、
$$
M''(0) = a(a+1)b^2
$$
よって分散は
$$
\text{Var}[X] = M''(0) - (M'(0))^2 = a(a+1)b^2 - (ab)^2 = ab^2
$$
以上より、γ分布の平均は $ ab $、分散は $ ab^2 $ であることが分かります。モーメント母関数からこれらの値を求めることができました。
ベータ分布
ベータ分布のモーメント母関数（MGF）は以下のように求められます：
$$
M(t) = \mathbb{E}[e^{tX}] = \int_{0}^{1} e^{tx} \frac{x^{\alpha-1} (1-x)^{\beta-1}}{B(\alpha, \beta)} dx
$$
一般的に、この積分は解析的に解くのが難しいため、具体的な形にはまとめられません。しかし、期待値（平均）と分散はモーメント母関数を使わずに計算することが一般的です。
- 平均（期待値）の計算
$\beta$分布の平均は、以下のように定義されます：
$$
E[X] = \frac{\alpha}{\alpha + \beta}
$$
- 分散の計算
$\beta$分布の分散は、以下のように定義されます：
$$
\text{Var}[X] = \frac{\alpha \beta}{(\alpha + \beta)^2 (\alpha + \beta + 1)}
$$
以上のように、ベータ分布の平均と分散はパラメータ $\alpha$ と $\beta$ だけで表され、モーメント母関数を使わずに容易に計算できます。それでも、モーメント母関数を用いたい場合は、一般的に数値的な方法を用いて求める必要があります。
分布の同一性の判定
from sympy import symbols, exp, plot
import matplotlib.pyplot as plt
import numpy as np
t = symbols('t')
n, p = 50, 0.5 # 二項分布のパラメータ
mu = n * p # 正規分布の平均
sigma2 = n * p * (1 - p) # 正規分布の分散
# 二項分布の積率母関数
mgf_binomial = (1 - p + p * exp(t)) ** n
# 正規分布の積率母関数
mgf_normal = exp(mu * t + 0.5 * sigma2 * t ** 2)
# sympyでプロットを生成
p1 = plot(mgf_binomial, (t, -1, 1), line_color='blue'\
, show=False, legend=True, label='Binomial MGF')
p2 = plot(mgf_normal, (t, -1, 1), line_color='red'\
, show=False, legend=True, label='Normal MGF')
# matplotlibでプロット
fig, ax = plt.subplots(figsize=(3, 2))
# sympyのプロットデータをmatplotlibに適用
for p in [p1, p2]:
for series in p:
ax.plot(*series.get_points(), label=series.label, color=series.line_color)
# グラフの設定
ax.legend()
ax.set_title('Comparison of MGFs')
ax.set_xlabel('t')
ax.set_ylabel('MGF')
plt.show()
$ t $ は「変化」または「変位」と見なすことができますが、確率変数の特定のモーメントに対する「感度」または「反応」を測るためのパラメータとも言えます。積率母関数 $ M(t) $ は $ t $ の関数として定義され、$ t $ が変わるにつれて、確率変数の各モーメント（期待値、分散、歪度、尖度など）の「影響」がどのように変化するかを示します。
特性関数
特性関数（Characteristic Function）は、確率変数または確率分布の「特性」を研究するための一つの手段です。特に、確率変数の全てのモーメント（期待値、分散、歪度、尖度など）を生成する関数として重要です。
確率変数 $X$ の特性関数 $ \phi(t) $ は以下のように定義されます。
$
\phi(t) = \mathrm{E}[e^{itX}] = \int e^{itx} f(x) dx
$
ここで、$ \mathrm{E} $ は期待値を、$ f(x) $ は $X$ の確率密度関数を、$ i $ は虚数単位をそれぞれ表します。
主な特性
- 一意性: 同じ確率分布は同じ特性関数を持ちます。
- 逆変換: 特性関数が存在すれば、その確率分布も一意に定まります。
- 畳み込みと分布の合成: 独立な確率変数 $ X $ と $ Y $ の和 $ Z = X + Y $ の特性関数は、$ X $ と $ Y $ の特性関数の積として表されます。
$
\phi_Z(t) = \phi_X(t) \phi_Y(t)
$
- モーメントの生成: $ n $ 次のモーメントは特性関数を $ t = 0 $ で $ n $ 回微分し、$ i^n $ で割ることで得られます。
$
\mathrm{E}[X^n] = \frac{1}{i^n} \left. \frac{d^n}{dt^n} \phi(t) \right|_{t=0}
$
応用
- 確率分布の同定: 二つ以上の確率分布が等しいかどうかを調べるために特性関数を用いることがあります。
- 大数の法則や中心極限定理の証明: 特性関数は確率論の基本的な定理を証明する際にも用いられます。
- 統計的推論: データから確率分布を推論する際に、特性関数を使って尤度関数を計算することがあります。
特性関数は確率論と統計学、信号処理、量子力学など、多くの分野で幅広く応用されています。
２項分布と正規分布の特性の比較
import matplotlib.pyplot as plt
import numpy as np
# パラメータ
n, p = 5, 0.5
mu = n * p
sigma2 = n * p * (1 - p)
# tの範囲
t = np.linspace(-10, 10, 500)
# 二項分布の特性関数
cf_binomial_real = np.real((1 - p + p * np.exp(1j * t)) ** n)
cf_binomial_imag = np.imag((1 - p + p * np.exp(1j * t)) ** n)
# 正規分布の特性関数
cf_normal_real = np.real(np.exp(1j * mu * t - 0.5 * sigma2 * t ** 2))
cf_normal_imag = np.imag(np.exp(1j * mu * t - 0.5 * sigma2 * t ** 2))
# プロット
fig, ax = plt.subplots(figsize=(8, 4))
plt.subplot(1, 2, 1)
plt.title('Real part')
plt.plot(t, cf_binomial_real, label='Binomial')
plt.plot(t, cf_normal_real, label='Normal')
ax.set_xlabel('t')
ax.set_ylabel('MGF')
plt.legend()
plt.subplot(1, 2, 2)
plt.title('Imaginary part')
plt.plot(t, cf_binomial_imag, label='Binomial')
plt.plot(t, cf_normal_imag, label='Normal')
ax.set_xlabel('t')
ax.set_ylabel('MGF')
plt.legend()
plt.suptitle('Comparison of Characteristic Functions')
plt.show()
ーーーーーーーーーーーーーーーーーーーーーーーー
Python3ではじめるシステムトレード【第2版】環境構築と売買戦略
「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。