Statsmodelsによる生存時間分析

2024年01月23日に生存時間分析の記事を自身の学習のノートとして投稿しましたが、読み返してみると有効であるとは思えないため、全面的に書き換えました。それまでの記事は
https://github.com/kshedden/survival_workshop?tab=readme-ov-file
の英語原文をChatGPTに翻訳させ加筆修正していました。しかし、2カ月たって読み返してみると生存時間分析のイメージが読んですぐにわかなかったので、専門に生存時間分析を行ったり、学んでいるわけではないのだけれど、副次的な知識として別分野の人にとって有効になるように書き換えたつもりです。間違いがあると思うのでコメントいただけると幸いです。再投稿日は2024年3月20日です。８８４

生存時間分析

生存時間分析は、イベント（例えば、病気の治癒、機械の故障、ローンの完済など）が発生するまでの時間を扱う統計学の一分野です。この分析では、生存時間の分布、イベント発生のリスク、および時間経過に伴うその他の関連する変数の影響を評価します。主な目的は、イベントまでの期間を理解し予測することであり、医療、工学、社会科学、経済学など幅広い分野で応用されています。生存時間分析は、打ち切りデータや競合リスクなど、特殊なデータ構造を扱うための手法も開発されており、パラメトリック、ノンパラメトリック、半パラメトリックモデルを用いて分析を行います。

１．基礎統計学と確率

生存時間分析における統計学と確率は、イベント発生までの期間とその確率を定量化する基礎を提供します。データから生存関数やハザード率を推定し、リスク因子の影響を評価することで、予測モデルの構築と意思決定を支援します。

a. 母集団と標本

ー　母集団

母集団は、研究の対象となる全体の集合です。例えば、特定の種類のがんに対する治療法の効果を調べる場合、その治療を受ける可能性のある全ての患者が母集団になります。生存時間分析では、この母集団から生存時間データを抽出して分析を行います。しかし、実際には母集団全体を研究することは不可能または非実用的なため、代わりに標本が使用されます。

ー　標本

標本は、母集団から選ばれた一部の個体の集合です。標本の選び方は、研究結果が母集団全体に適用可能であることを確実にするために非常に重要です。例えば、上記のがん治療研究では、様々な年齢、性別、病期の患者をランダムに選択して標本とすることが理想的です。この標本から得られる生存時間データを分析することで、治療法の効果に関する推測が可能になります。

ー　生存時間分析における応用

生存時間分析では、標本から得られるデータを用いて、母集団における生存時間の分布を推定します。この分析により、特定の治療法が生存時間にどのような影響を与えるか、また、年齢や性別などの他の要因が生存時間にどのような影響を与えるかを理解することができます。重要なのは、標本が母集団を適切に代表しているかどうかです。これが確実であれば、標本から得られる結果を母集団全体に一般化することが可能になります。

生存時間分析を行う際には、打ち切りデータや競合リスクなどの特殊な問題にも対処する必要があります。これらは生存時間データが持つ独特の特性であり、母集団と標本の関係を考える上で特に注意を要します。例えば、打ち切りデータは、研究期間中にイベントが発生しなかった個体に関する情報を扱います。これらの特性を考慮することで、より正確な生存時間の推定と分析が可能になります。

b. 確率分布と生存時間の基本原理

生存時間分析において、確率分布はイベント（例えば、疾病からの回復、機械の故障、あるいは人の死亡など）が発生するまでの時間の変動をモデル化するために用います。このセクションでは、生存時間を記述するための基本的な概念である確率密度関数 $f(t)$、生存関数 $S(t)$、累積分布関数 $F(t)$ の関係、そしてそれらに関連するイベント確率と限界イベント確率について解説します。

• 確率密度関数 $f(t)$: $f(t)$ は、特定の瞬間 $t$ でのイベント発生の密度を表します。直接的にイベントが発生する「確率」を示すものではありません。時間 $t$ におけるイベント発生の確率を得るためには、$f(t)$ をある区間にわたって積分する必要があります。

• 累積分布関数 $F(t)$: $F(t)$ は時間 $t$ までにイベントが少なくとも一度発生する確率を示し、$F(t) = \int_0^t f(u) du$ で正しく計算されます。これは、時間経過に伴うイベント発生の累積確率を示します。

• 生存関数 $S(t)$: $S(t)$ は、時間 $t$ までにイベントが発生しない確率を示し、$S(t) = 1 - F(t)$ で定義されます。これは累積分布関数 $(F(t))$の補数として定義されます。生存関数は、ある時点まで生存する確率を直感的に理解するのに適しています。

• 累積確率と限界イベント確率: 生存時間分析では、イベント（例えば、死亡や故障など）が時間経過と共にどのように発生するかを評価するために、累積確率と限界イベント確率という二つの基本概念を用います。

ー　限界イベント確率：限界イベント確率は、ある時間区間でイベントが発生する条件付き確率を示します。これは、その期間の開始時点でイベントがまだ発生していない個体に対するイベント発生の確率です。限界イベント確率は、特定の時間区間におけるイベント発生の即時的なリスクを反映します。

ー　累積確率：累積確率（または累積分布関数）は、開始時点からある特定の時間点までにイベントが発生する全体的な確率を示します。これは、時間が経過するにつれて蓄積されるイベント発生の確率を表し、イベントがその時点までに少なくとも一度発生する可能性を示します。累積確率は、時間の経過に伴うイベントの発生傾向全体を把握するために用いられます。

限界イベント確率と累積確率は、生存時間データを分析し、イベント発生のダイナミクスを理解するために重要な概念です。限界イベント確率は、特定の短い期間内のリスクに焦点を当てるのに対し、累積確率はより長い時間軸にわたるイベント発生の全体的なパターンを捉えるために用います。

ー　簡単な例：この例では、初期の患者数が100人で、1か月後に5名、続いて2か月後にさらに5名が死亡する状況を考えます。

時間（月）	生存している患者数	期間内の死亡者数	限界死亡率	生存率 $S(t)$	累積死亡率 $F(t)$
0	100	-	-	1.0	0
1	95	5	5/100	0.95	0.05
2	90	5	5/95	0.9026	0.0974

• 生存している患者数: 特定の時点で生存している患者の数です。
• 期間内の死亡者数: 各期間内に死亡した患者の数です。
• 限界死亡率: 各期間内での死亡した患者の割合です。例えば、1か月目の限界死亡率は、期間開始時の生存者数に対する死亡者数の比率（5/100）です。
• 生存率 $S(t)$: 時間 $t$ までに生存している確率です。生存率は、1から各期間の限界死亡率の積を引いた値で計算されます。例えば、2か月後の生存率は、$1 - (1 - 5/100) \times (1 - 5/95)$ です。
• 累積死亡率 $F(t)$: 時間 $t$ までに少なくとも一度死亡する確率です。累積死亡率は、生存率の補数として計算され、$1 - S(t)$ によって得られます。

限界死亡率、生存率、累積死亡率により時間が経過するにつれて生存率がどのように変化し、それに伴って累積死亡率がどのように増加するかを示すことができます。

c. 確率変数

生存時間分析において、確率変数は研究対象となるイベント（例えば、疾病からの回復、機械の故障、ローンの完済など）が発生するまでの時間を表します。この分野で扱う確率変数は、通常、連続確率変数ですが、離散確率変数を用いる場合もあります。以下では、生存時間分析の文脈で確率変数をどのように理解し、利用するかについて説明します。

ー　生存時間と確率変数

生存時間分析における主な関心事は、特定のイベントまでの時間、すなわち生存時間です。この生存時間を表すために、確率変数 $T$ を使用します。$T$ は非負の実数を取り、特定の個体が観測開始からイベント発生まで生存する時間を示します。たとえば、ある疾患に対する新しい治療法の効果を評価する研究では、治療開始から患者が特定の健康状態に到達するまでの時間、または追跡調査期間中に亡くなるまでの時間が $T$ によって表されます。

ー　確率変数の分布

生存時間 $T$ の確率分布（例えば、指数分布、ワイブル分布など）は、時間経過に伴うイベント発生の確率をモデル化します。この分布から、生存関数 $S(t) = P(T > t)$、つまり時間 $t$ までにイベントが発生しない確率、またはハザード関数 $h(t)$、時間 $t$ での瞬間的なイベント発生率を導出できます。生存関数とハザード関数は、生存時間データの分析と解釈において中心的な役割を果たします。

ー　生存時間データの特徴

生存時間分析で扱う確率変数は、いくつかの特有の特徴を持ちます。特に重要なのは、右側打ち切りデータと競合リスクです。

• 右側打ち切り: 研究の終了時点までにイベントが発生していない場合、そのデータは右側打ち切りとみなされます。これは、生存時間 $T$ が観測期間を超えることを意味し、確率変数の実際の値が不明であることを示します。
• 競合リスク: 複数の異なるイベントが対象者に発生する可能性がある場合、これらのイベントは競合リスクを形成します。たとえば、がん患者においては、がんに関連する死亡とがんとは無関係な理由での死亡が考えられます。

d. 期待値

生存時間分析における期待値は、特定のイベントまでの平均時間を示す統計的尺度です。具体的には、生存時間の確率変数 $T$ の期待値 $E[T]$ は、個体がイベント（例えば、疾病の回復、機械の故障、ローンの完済）に到達するまでの平均時間を表します。この平均生存時間は、さまざまな条件下での生存率や治療法の効果を評価するために使用されます。

ー　期待値の定義

期待値 $E[T]$ は、生存時間 $T$ の全可能な値にわたる確率加重平均として定義されます。数学的には、連続確率変数の場合、期待値は次のように表されます：

$$ E[T] = \int_0^\infty t \cdot f(t) , dt $$

ここで、$f(t)$ は $T$ の確率密度関数です。この式は、すべての可能な生存時間にわたってそれぞれの時間 $t$ が発生する確率を考慮に入れた平均を計算します。

ー　生存時間分析における期待値の意義

生存時間分析では、期待値は患者の平均生存期間や製品の平均故障までの時間など、研究の対象となるイベントの平均発生時間を理解するために重要です。例えば、二つの異なるがん治療法を比較する際、それぞれの治療法における患者の平均生存期間を比較することで、どちらの治療法がより効果的かを評価できます。

ー　期待値と生存関数

生存時間分析では、生存関数 $S(t)$ と密接に関連して、期待値が計算されます。生存関数は、時間 $t$ までにイベントが発生しない確率を示す関数であり、期待値はこの生存関数からも導出できます：

$$ E[T] = \int_0^\infty S(t) , dt $$

この式は、ある時点まで生存している確率の全時点にわたる積分として期待値を表します。つまり、すべての時間点で生存する確率の合計が、平均生存時間に等しいことを意味します。

ー　実践的な応用

生存時間の期待値を計算することは、医療研究において患者の予後を評価するため、製品の信頼性工学において製品の寿命を推定するため、金融リスク管理においてクレジット契約の期待寿命を評価するためなど、多岐にわたる分野で重要です。期待値の分析を通じて、研究者や実務家はより効果的な意思決定を行い、リスクを管理し、政策や治療戦略を策定するための重要な洞察を得ることができます。

e. 時系列データの基本

生存時間分析の文脈において、時系列データの基本を理解することは、時間とともに変化するイベントや状態を追跡し分析する上で重要です。生存時間分析は、特定のイベント（例えば、患者の死亡、機械の故障、ローンの完済など）が発生するまでの時間を扱うため、時系列データの一種と考えることができます。このセクションでは、時系列データの基本概念とその生存時間分析への応用について説明します。

ー　時系列データの特徴

時系列データは、時間的順序に沿って連続的または一定間隔で収集されたデータ点の系列です。この種のデータは、時間とともに変化する現象を観察し、分析するために使用されます。生存時間分析における時系列データの重要な特徴には、以下が含まれます：

• 時間依存性：時系列データの値は、時間の経過と共に相互に関連しています。たとえば、患者の健康状態は時間と共に変化し、過去の状態が将来の状態に影響を与える可能性があります。
• 季節性：一定の周期で繰り返されるパターンを示すことがあります。生存時間分析では、季節性はあまり一般的ではありませんが、特定の条件やイベント（例えば、感染症の季節的発生）において重要になることがあります。
• トレンド：データが長期にわたって増加または減少する傾向を示すことがあります。治療法の改善によって患者の生存時間が延びる場合などがこれに該当します。

ー　生存時間分析への応用

生存時間分析では、時系列データの扱い方が特に重要になります。以下はその応用例です：

• 時間変動共変量の扱い：患者の年齢や治療法など、時間と共に変化する可能性のある要因（共変量）を考慮する必要があります。これらの共変量の時間による変化を適切にモデル化することで、生存時間に及ぼす影響をより正確に推定できます。
• イベント履歴分析：個体が複数のイベントを経験する場合、それぞれのイベントの発生時点と順序を記録することで、イベント間の関連性や因果関係を分析できます。
• リスクセットの構築：生存時間分析では、特定の時点でイベントが発生するリスクを評価するために、その時点までイベントが発生していない個体の集合（リスクセット）を使用します。

ー　時系列データの分析技術

生存時間分析における時系列データの分析には、コックス比例ハザードモデルや加速故障時間モデル（AFTモデル）などの特定の統計モデルが使用されます。これらのモデルは、時間変動共変量を含むデータを扱う能力を持ち、生存時間に対する様々な因子の影響を推定するために役立ちます。

生存時間分析における時系列データの理解と適切な扱いは、時間とともに変化する現象を正確に分析し、有意義な結論を導き出すために不可欠です。

２．生存時間データの特性：

a. 打ち切り

生存時間分析における打ち切りデータは、研究において非常に一般的な現象であり、特にこの分野のデータ解析における独特な課題を提起します。打ち切りデータは、イベント（例えば、患者の死亡、機械の故障、ローンの完済など）が観測期間内に発生しないケースを指します。これは、データ収集が終了した時点で、イベントがまだ起こっていないか、あるいは追跡が途中で終了したため、完全な生存時間を観測できない状況を示します。

ー　打ち切りの種類

打ち切りには主に三つの種類があります：

1. 右側打ち切り：最も一般的な形式で、研究終了時点でイベントがまだ発生していない場合に生じます。例えば、研究期間が終了した時点で生存している患者は、右側打ち切りデータとなります。

2. 左側打ち切り：イベントが研究開始前に発生している場合に生じます。これは、研究開始時点で既にイベントが発生していたため、その正確な発生時点が不明なデータを指します。

3. 間隔打ち切り：イベントが二つの訪問または観測の間に発生したが、正確なタイミングが不明な場合に生じます。

ー　打ち切りデータの影響

打ち切りデータは、生存時間分析における推定と解釈を複雑にします。打ち切りを無視して分析を行うと、生存時間の推定値が歪み、誤った結論に至る可能性があります。例えば、右側打ち切りデータを含む分析では、打ち切りされた観測値を単純に除外すると、平均生存時間を過小評価する結果となる可能性があります。

ー　打ち切りデータの扱い方

打ち切りデータを適切に扱うためには、それを考慮に入れた統計モデルを使用する必要があります。コックス比例ハザードモデルやカプラン・マイヤー生存曲線などの手法は、打ち切りデータを考慮に入れて生存時間を推定するために広く用いられています。これらの手法は、打ち切り情報を利用して、生存時間の分布に関するより正確な推定を提供します。

生存時間分析における打ち切りデータの適切な扱いは、信頼性の高い結果を得るために不可欠です。これにより、研究者はより正確な生存率の推定、リスク因子の影響の評価、異なる群間での生存時間の比較などを行うことができます。

b. 共変量：

生存時間分析における共変量は、生存時間に影響を与える可能性がある任意の変数です。これらは、個体の特性（例えば、年齢、性別、既往歴）、治療方法（例えば、薬物療法、手術）、環境要因（例えば、喫煙状況、職業暴露）、または時間変動共変量（時間とともに変化する特性や状態）など、研究の目的や設計に応じてさまざまです。共変量の分析は、生存時間とこれらの変数との関連を理解し、評価することを目的としています。

ー　共変量の重要性

共変量は、生存時間に影響を及ぼす様々な因子を理解するために不可欠です。これらの変数を分析に組み込むことで、異なる群間での生存時間の違いを説明したり、特定の治療が生存に与える効果を調整したりすることができます。また、共変量を考慮することで、予後の良い患者群とそうでない患者群を同定することも可能になります。

ー　共変量の扱い方

生存時間分析で共変量を扱う主な方法には、コックス比例ハザードモデルがあります。このモデルは、共変量の効果を生存時間に対するリスク比としてモデル化し、共変量が生存時間に与える相対的なリスクの増減を推定します。コックスモデルは、共変量が時間とともに一定であることを前提としていますが、時間変動共変量を含めることも可能です。

ー　共変量の分析の挑戦

共変量を生存時間分析に組み込む際にはいくつかの挑戦があります。例えば、共変量間の相関（多重共線性）や、時間によって変化する共変量の扱いなどです。多重共線性は、モデルの推定を不安定にする可能性があり、正確な結果の解釈を困難にします。また、時間変動共変量は、分析の複雑さを増す可能性があり、これを適切にモデル化するためには特別な注意が必要です。

ー　実践的応用

共変量の分析を通じて、研究者は治療法の効果をより正確に評価したり、特定のリスク因子が生存にどのように影響するかを理解したりすることができます。これにより、リスクの高い患者群を特定し、個別化医療の実現や、より効果的な治療戦略の開発につなげることが可能になります。

共変量の考慮は、生存時間分析において、より深い洞察を得るための重要なステップです。適切な統計モデルの選択と共変量の慎重な分析により、より信頼性の高い結果と有意義な結論を導くことができます。

c. 競合リスク

生存時間分析における競合リスクは、研究対象となる特定のイベントの発生を他の一つ以上のイベントが妨げる状況を指します。つまり、あるイベントが発生する前に別のイベントが起こることで、最初のイベントが観測されなくなる可能性がある場合、これらのイベントは競合リスクの関係にあります。この概念は、生存時間データの分析において重要な考慮事項であり、特に医療研究や信頼性工学などの分野で顕著です。

ー　競合リスクの例

例えば、がん患者の生存分析を行う場合、目的イベントが特定のがんによる死亡であるとします。この場合、がん以外の原因での死亡も起こり得るため、がん以外の原因で死亡するケースは、特定のがんによる死亡の観測を妨げる競合リスクとなります。

ー　競合リスクの影響

競合リスクの存在は、生存時間分析の結果に大きな影響を与える可能性があります。競合リスクを無視して通常の生存分析を行った場合、特定のイベントのリスクを過大評価することになりかねません。これは、全てのタイプのイベントを単一のイベントとして扱うことで、実際には別のイベントによって生存時間が短縮されている可能性があるにも関わらず、目的イベントに対するリスクが高いように見えるためです。

ー　競合リスクの分析方法

競合リスクの存在を考慮した分析には、特定の手法が必要です。一般的なアプローチには、ファイン＆グレイモデルなどのサブディストリビューションハザードモデルがあります。これらのモデルは、競合リスクを直接的に考慮に入れ、特定のイベントの絶対リスク推定を提供します。また、カプラン・マイヤー法などの従来の生存分析手法とは異なり、これらの手法は競合リスクの影響を適切に反映させることができます。

ー　競合リスクの扱いの重要性

競合リスクを適切に扱うことは、特に複数の異なるイベントが関与する研究において重要です。これにより、各イベントの真のリスクをより正確に推定し、誤解を招く可能性のある結論を避けることができます。例えば、医療研究では、特定の治療が特定の病気に対してどの程度効果的かを評価する際に、他の原因による死亡リスクを考慮に入れることが不可欠です。

生存時間分析における競合リスクの考慮は、研究の設計段階から重要な側面となります。分析計画を立てる際には、競合リスクをどのように扱うかを予め考慮し、適切な統計手法を選択することが重要です。これにより、より信頼性の高い結果を得ることが可能になり、研究の有効性を高めることができます。

３．生存時間とハザードレート

a. 生存時間

生存時間分析における「生存時間」とは、観測開始から特定のイベント（例えば、疾病の回復、機械の故障、あるいは死亡など）が発生するまでの時間を指します。生存時間は、研究の目的に応じて、人の生命期間、製品の使用可能期間、契約の継続期間など、様々な形で解釈されます。この時間は通常、非負の連続変数として扱われ、生存時間データとして分析されます。

ー　生存関数

生存時間の分析では、「生存関数」が中心的な役割を果たします。生存関数 $S(t)$ は、時間 $t$ までに特定のイベントが発生しない確率を示す関数です。数学的には、生存関数は次のように定義されます：

$$ S(t) = P(T > t) $$

ここで、$T$ はイベント発生までの時間の確率変数、$t$ は特定の時間点です。生存関数は、時間が進むにつれて減少する性質を持ち、最終的には全ての個体がイベントを経験するため、時間が無限大になると $S(t)$ は0に近づきます。

b. ハザードレート

生存時間分析における「ハザードレート」は、ある時点でイベント（例えば、疾病の回復、機械の故障、死亡など）が発生する瞬間的なリスクまたは危険度を表す指標です。ハザードレートは、時間の関数として定義され、特定の時間におけるイベント発生の条件付き確率を示します。これは生存時間分析において、イベントの発生傾向を理解する上で非常に重要な概念です。

ー　ハザードレートの定義

ハザードレート $h(t)$ は、時間 $t$ におけるイベント発生の瞬間的なリスクを表し、次のように定義されます：

$$ h(t) = \lim_{\Delta t \to 0} \frac{P(t \leq T < t + \Delta t | T \geq t)}{\Delta t} $$

ここで、$T$ はイベント発生までの時間の確率変数、$t$ は特定の時間点、$\Delta t$ は非常に小さい時間の区間です。この式は、時間 $t$ 以降にイベントが発生する条件下で、時間 $t$ から $t + \Delta t$ までの間にイベントが発生する確率の割合を表しています。

ー　ハザード関数と生存関数の関係

ハザード関数 $h(t)$ と生存関数 $S(t)$ は密接に関連しており、一方から他方を導出することができます。生存関数は、時間 $t$ までにイベントが発生しない確率を示し、ハザード関数は、その時点でイベントが発生する瞬間的なリスクを示します。具体的には、ハザード関数は生存関数から次のように導かれます：

$$ h(t) = -\frac{d}{dt}\ln S(t) $$

ー　累積分布関数とハザードレート

累積分布関数 $F(t)$ は、時間 $t$ までにイベントが発生する確率を示し、生存関数 $S(t)$ の補数として定義されます。ハザードレート $h(t)$ は、時間 $t$ におけるイベント発生の瞬間的なリスクを表し、累積分布関数 $F(t)$ と次のような関係にあります：

$$ h(t) = \frac{f(t)}{S(t)} = \frac{f(t)}{1 - F(t)} $$

ここで、$f(t)$ は確率密度関数です。また、累積ハザード関数 $H(t)$ はハザードレート $h(t)$ の積分であり、累積分布関数 $F(t)$ と密接に関連しています：

$$ H(t) = \int_0^t h(u) du = -\ln(S(t)) $$

この式から、累積分布関数 $F(t)$（または生存関数 $S(t)$）は、ハザードレート $h(t)$ の関数であることがわかります。これにより、ハザードレートの形状が生存時間の分布に直接影響を与えることが示されます。

ー　ハザードレートの応用

ハザードレートは、生存時間データを分析する際に、時間経過と共にイベントのリスクがどのように変化するかを理解するために使用されます。例えば、医療研究では、新しい治療法が時間とともに患者の生存率にどのような影響を与えるかを評価するために、ハザードレートを分析することがあります。また、製品の信頼性を評価する際には、製品の故障リスクが時間とともにどのように変化するかを調べるためにハザードレートが利用されます。

ー　ハザードレートのモデリング

ハザードレートをモデル化することで、さまざまな共変量がイベント発生のリスクにどのように影響するかを評価できます。最も一般的なモデルの一つがコックス比例ハザードモデルであり、これはハザードレートが共変量の線形関数と比例関係にあると仮定します。このモデルは、共変量の影響を解析し、異なる群間でのハザードレートの比較を可能にします。

ハザードレートの分析を通じて、研究者や実務家はイベント発生のダイナミクスをより詳細に理解し、リスク要因の同定や予防策の策定、治療法の改善に役立つ洞察を得ることができます。

５．生存時間分析の分類

a. パラメトリック

生存時間分析におけるパラメトリックモデルは、生存時間データの分布を特定の確率分布でモデル化するアプローチです。これらのモデルは、生存時間の分布に関して具体的な数学的形式を仮定し、その分布を定義するパラメーターを用いてデータを分析します。パラメトリックモデルの利用により、生存関数、ハザード関数、および他の生存時間関連の量を明示的な形式で表現し、推定することが可能になります。

ー　パラメトリックモデルの種類

生存時間データをモデル化するために一般的に使用されるパラメトリック分布には、以下のようなものがあります：

• 指数分布: 指数分布は、ハザードレートが時間に依存せず一定である場合（メモリレス性）に適用されます。これは、イベントの発生率が一定であるシナリオに適したモデルです。
• ワイブル分布: ワイブル分布は、ハザードレートが時間と共に増加または減少する場合に使用されます。形状パラメータによってハザードレートの時間依存性を調整し、より柔軟なモデリングが可能です。
• 対数正規分布: 対数正規分布は、生存時間の対数が正規分布に従うと仮定するモデルです。この分布は、生存時間に正の歪みがある場合に適しています。
• ガンマ分布: ガンマ分布は、ハザードレートが時間と共に単調ではなく、最初に増加してから減少するような場合に使用されます。
• アクセラレーテッドフェイルアタイム（Accelerated Failure Time, AFT）モデル: このモデルは、生存時間に影響を与える共変量の効果をモデル化し、特定の確率分布を仮定して生存時間の分布を直接モデリングします。AFTモデルでは、対数生存時間が共変量の線形結合として表されると仮定します。その形式は以下のようになります：$ \log(T) = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_pX_p + \sigma\epsilon $ここで、$T$は生存時間、$X_1, X_2, ..., X_p$は共変量、$\beta_0, \beta_1, ..., \beta_p$は共変量の効果を表すパラメータ、$\sigma$はスケールパラメータ、$\epsilon$は誤差項であり、特定の確率分布に従います（例えば正規分布、対数正規分布、ワイブル分布など）。

ー　パラメトリックモデルの利点

パラメトリックモデルは、生存時間分布の明確な数学的表現を提供します。これにより、生存関数やハザード関数の明確な形式が得られ、生存時間に関する予測や、異なる群間の比較、共変量の効果の定量化が容易になります。また、パラメトリックモデルを使用すると、データ外挿やリスク予測など、非パラメトリック手法では難しい分析が可能になる場合があります。

ー　パラメトリックモデルの制限

パラメトリックモデルの主な制限は、生存時間データの分布に関して特定の仮定を置く必要がある点です。これらの仮定がデータに適合しない場合、モデルの推定結果は偏る可能性があります。したがって、適切なパラメトリックモデルを選択するためには、データの前処理と探索的分析が重要です。

ー　実践的応用

パラメトリックモデルは、医療研究における患者の生存期間の予測、信頼性工学における製品寿命の推定、経済学におけるイベント発生までの期間のモデリングなど、さまざまな分野で応用されます。適切なモデルを選択し、データに適合させることで、生存時間に関連する重要な洞察を得ることができます。

b. ノンパラメトリックモデル

生存時間分析におけるノンパラメトリックモデルは、生存時間データの分析において、特定の確率分布に対する仮定を設けずに生存関数を推定するアプローチです。これらのモデルは、データの構造やパターンから直接生存関数やハザード関数を推定することに焦点を当てており、さまざまな形状の生存時間分布に柔軟に対応できる利点があります。

ー　ノンパラメトリックモデルの特徴

ノンパラメトリック手法の最大の特徴は、生存時間分布に関する厳密な仮定を必要としない点です。これにより、データが従う分布が未知であったり、複数の異なる要因によって影響を受ける複雑なケースにおいても、データの実際の挙動をより忠実に捉えることが可能になります。

ー　主なノンパラメトリック手法

• カプラン・マイヤー推定器: 最も一般的な生存関数の推定方法の一つで、各時間点での生存率を段階的に計算し、生存曲線を描くことができます。カプラン・マイヤー推定器は、右側打ち切りデータを効果的に取り扱うことができるため、臨床試験や生存時間研究で広く使用されています。

カプラン・マイヤー推定法による生存関数 $S(t)$ の推定値は、以下のように計算されます：

$$ \hat{S}(t) = \prod_{t_i \leq t} \left(1 - \frac{d_i}{n_i}\right) $$

ここで、$t_i$ はイベントが発生した時点（観察された生存時間）、$d_i$ は時点 $t_i$ で発生したイベントの数、$n_i$ は時点 $t_i$ でリスクセットに含まれる個体の数（つまり、時点 $t_i$ までにイベントが発生していない個体の数）を表します。この積の形式は、各時点での生存確率の積として全体の生存確率を求めることを意味しています。

• ネルソン・アーレン推定器: 累積ハザード関数を推定するために使用される方法で、特にイベント発生が比較的まれなケースで有効です。ネルソン・アーレン推定器は、時間経過とともにイベントのリスクがどのように変化するかを評価するために使用されます。

ネルソンアーレン推定器による累積ハザード関数 $H(t)$ の推定値は、観察されたイベント発生時間までの各時点 $t$ において、次のように計算されます：

$$ \hat{H}(t) = \sum_{t_i \leq t} \frac{d_i}{n_i} $$

ここで、$t_i$ はイベントが発生した時点、$d_i$ は時点 $t_i$ で発生したイベントの数、$n_i$ は時点 $t_i$ でリスクセットに含まれる個体の数（つまり、時点 $t_i$ までにイベントが発生していない個体の数）を表します。

ー　ノンパラメトリックモデルの利点と制限

利点:

• 分布に関する事前の仮定が不要であるため、データの探索的分析に最適です。
• 打ち切りデータを自然に取り扱うことができ、現実の生存時間データ分析に適しています。

制限:

• 推定された生存関数はデータに依存するため、小さなサンプルサイズでは推定が不安定になる可能性があります。
• 共変量の影響を直接モデル化することはできず、別のアプローチ（例えば、コックス比例ハザードモデル）を用いる必要があります。
• データの外挿や複雑な予測モデルの構築には適していません。

ー　実践的応用

ノンパラメトリック手法は、医療研究、信頼性工学、生物統計学など、生存時間データが重要な役割を果たす多くの分野で基本的な分析ツールとして使用されます。これらの手法により、生存時間データの基本的な特性を明らかにし、さらに詳細な分析のための基盤を提供します。

c. 半パラメトリックモデル

生存時間分析における半パラメトリックモデルは、パラメトリックモデルとノンパラメトリックモデルの特徴を組み合わせたアプローチです。これらのモデルは、生存時間データの分析において、一部の構成要素にパラメトリックな仮定を置きつつ、他の部分ではそのような仮定を設けずにデータから直接情報を得る方法を提供します。半パラメトリックモデルの中で最も一般的に使用されるのが、コックス比例ハザードモデルです。

ー　コックス比例ハザードモデル

コックス比例ハザードモデルは、生存時間分析で広く使用される半パラメトリックモデルの一つであり、ハザードレートが時間に依存する形で共変量の効果をモデル化します。このモデルの基本形式は次のように表されます：

$$ h(t) = h_0(t) \exp(\beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p) $$

ここで、$h(t)$ は時間 $t$ におけるハザードレート、$h_0(t)$ は基準ハザード関数（時間によって変化するが、モデルでは未指定の形式）、$X_1, X_2, \ldots, X_p$ は共変量、$\beta_1, \beta_2, \ldots, \beta_p$ は共変量の効果を表すパラメーターです。

ー　サブディストリビューションハザードモデル

特にファイン＆グレイモデルは、競合リスクが存在する生存時間データの分析に用いられ、特定のイベントのリスク（ハザード）を、他の競合するイベントの存在下で推定することを目的としています。ファイン＆グレイモデルの基本形式は以下のように表されます：

$$ \tilde{h}(t) = \tilde{h}_0(t) \exp(\beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p) $$

ここで、

• $\tilde{h}(t)$ は特定のイベントタイプに対する時間 $t$ におけるサブディストリビューションハザードレートです。
• $\tilde{h}_0(t)$ はサブディストリビューション基準ハザード関数で、時間によって変化しますが、モデルでは具体的な形式は指定されていません。
• $X_1, X_2, \ldots, X_p$ は共変量です。
• $\beta_1, \beta_2, \ldots, \beta_p$ は共変量の効果を表すパラメーターで、これらのパラメーターは特定のイベントのリスクに対する共変量の影響の大きさと方向を示します。

ー　半パラメトリックモデルの特徴

• 柔軟性: 基準ハザード関数 $h_0(t)$ に特定の形式を仮定せず、データから直接推定することで、様々な形状のハザード関数に対応できます。
• 共変量の効果の解釈: 共変量の効果はパラメトリックな形式でモデル化されるため、共変量がハザードレートに与える相対的な影響の解釈が容易になります。
• 広範な応用: 医療研究での患者の生存率分析、製品の信頼性評価、社会科学でのイベント発生までの時間分析など、多岐にわたる分野で適用可能です。

ー　半パラメトリックモデルの利点と制限

利点:

• 共変量の効果を明確に評価でき、異なる群間や治療間の比較が可能です。
• 基準ハザード関数に形式を仮定しないため、モデルの柔軟性が高いです。

制限:

• 基準ハザード関数の具体的な形はモデルから直接得られないため、その挙動を詳細に理解することは難しい場合があります。
• モデルの仮定、特に比例ハザードの仮定が適切であるかどうかを検証する必要があります。

半パラメトリックモデル、特にコックス比例ハザードモデルは、生存時間分析においてバランスの取れた選択肢となり得ます。これは、生存時間データの複雑さと多様性に対応するための柔軟性と、統計的推定の正確さを提供するための適度なパラメトリック仮定を組み合わせることができるためです。特に、共変量の影響を時間とともに一定と仮定する比例ハザードの条件下で、さまざまなリスク因子が生存時間に与える影響を定量的に評価する場合に有効です。しかしながら、比例ハザードの仮定の妥当性を確認すること、またデータに適したモデル選択を行うことが、信頼性の高い分析結果を得るために重要です。半パラメトリックモデルを使用する際には、これらの制限とともに、モデルの解釈と応用における注意点を考慮する必要があります。

６．実データを用いた分析：コックス比例ハザードモデル、カプラン・マイヤー推定器、AFTモデル(アクセラレーテッドフェイルアタイムモデル)

生存時間分析の3つの主要な手法であるコックス比例ハザードモデル、カプラン・マイヤー推定器、アクセラレーテッドフェイルアタイム（AFT）モデルについて、Pythonのライブラリlifelinesを使用して説明し、それぞれのコード例を示します。lifelinesは生存時間分析を行うための強力なライブラリであり、これらの手法を簡単に実装できます。

まず、分析の前準備として、必要なライブラリをインストールし、データセットを準備します。ここでは、lifelinesに含まれる架空のデータセットを使用します。

!pip install lifelines

# ライブラリのインポート
import numpy as np
import pandas as pd
from lifelines import KaplanMeierFitter, CoxPHFitter, WeibullAFTFitter
from lifelines.datasets import load_rossi

# データセットの読み込み
data = load_rossi()

rossiデータセットは、lifelinesライブラリに含まれる生存時間分析用のサンプルデータセットの一つです。このデータは、1980年にアメリカの犯罪学者であるRossiらによって収集されたもので、元囚人たちが釈放された後に再び逮捕されるまでの期間（リサイディビズム、すなわち再犯率の研究）を調査するために使用されました。

データセットの特徴

rossiデータセットには、元囚人たちの様々な属性や、釈放後に再逮捕されたかどうかのイベント発生情報が含まれています。主な変数には以下のようなものがあります：

• week: 釈放されてから再逮捕されるまでの週数。この変数は生存時間を表します。
• arrest: 再逮捕されたかどうかの指標（1が再逮捕、0が再逮捕されず）。この変数はイベント発生の有無を表します。
• fin: 財政支援を受けたかどうか（1が受けた、0が受けなかった）。
• age: 釈放時の年齢。
• race: 人種（1が黒人、0がその他）。
• wexp: 釈放前に正式な雇用経験があるかどうか（1がある、0がない）。
• mar: 結婚しているかどうか（1が結婚している、0がそうでない）。
• paro: 釈放時に仮釈放中であるかどうか（1が仮釈放、0が非仮釈放）。
• prio: 過去の逮捕回数。

このデータセットは、生存時間分析の手法を理解し、実践するための教育的な例としてよく使用されます。特に、コックス比例ハザードモデルやカプラン・マイヤー推定器などのモデルを適用して、どのような要因が再逮捕までの期間に影響を与えるかを分析するのに役立ちます。

利用例

rossiデータセットを利用することで、生存分析の基本的な概念やモデリング手法を実際のデータに適用する方法を学ぶことができます。分析の過程で、特定の共変量が再逮捕までの期間にどのような影響を持つかを評価し、リスク要因を同定することが可能になります。これにより、再犯防止策を検討するための有益な洞察を得ることができます。

   week	arrest	fin	　age	race	wexp	mar	paro	prio
0	20	　1	　　0	　　27	　1	　　0	　　　0	1	　　3
1	17	　1	　　0	　　18	　1	　　0	　　　0	1	　　8
2	25	　1	　　0	　　19	　0	　　1	　　　0	1	　 13
3	52	　0	　　1	　　23	　1	　　1	　　　1	1	　　1

a. カプラン・マイヤー推定器

カプラン・マイヤー推定器は、生存関数を非パラメトリックに推定する方法です。これは、各イベント発生時点での生存確率を段階的に計算します。

# カプラン・マイヤー推定器のインスタンス化とフィット
kmf = KaplanMeierFitter()
kmf.fit(durations=data["week"], event_observed=data["arrest"])

# 生存関数のプロット
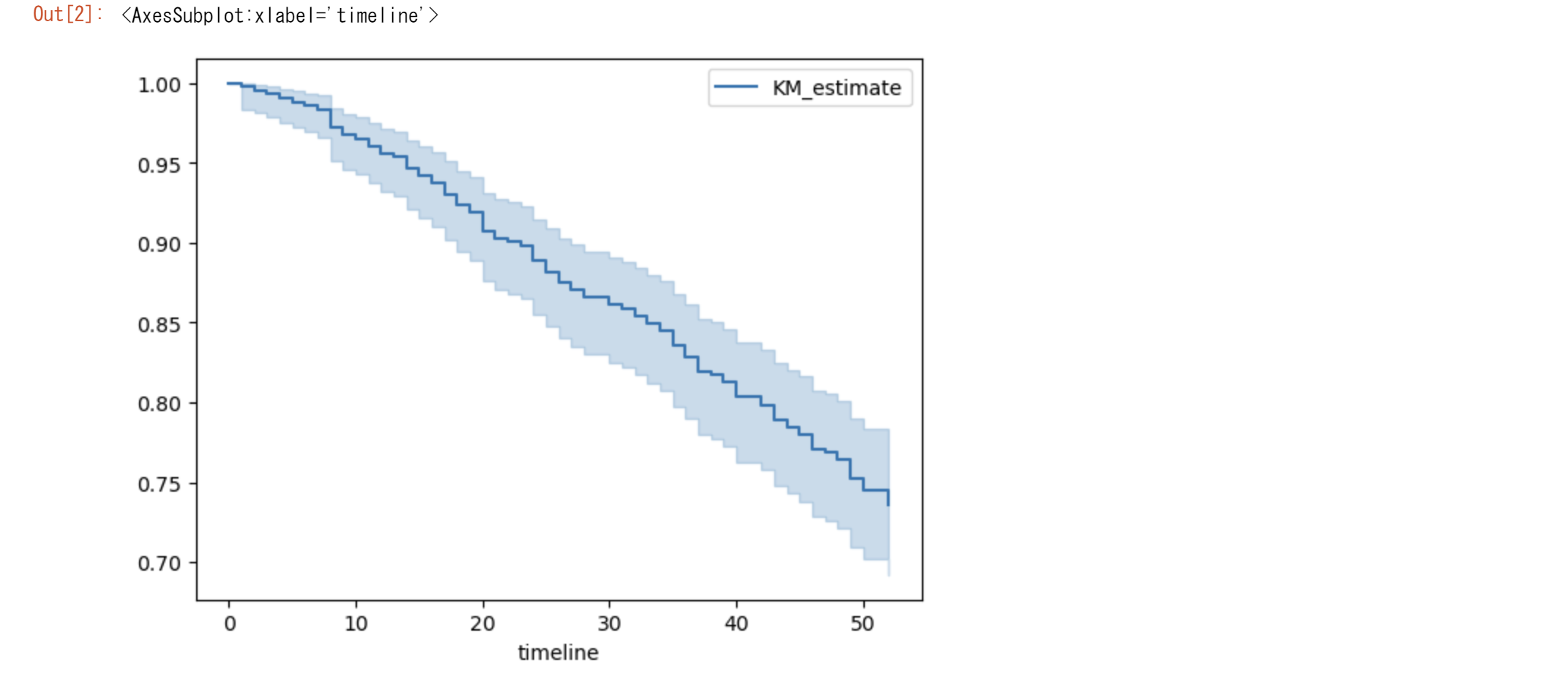
kmf.plot_survival_function()

rossi データセットには、観察期間内に再逮捕されなかった（つまり、イベントが発生しなかった）個体が含まれており、これらは右側打ち切りデータとして扱われます。カプランマイヤー推定器は、これらの打ち切りデータを適切に処理し、全体の生存関数を推定することができます。

打ち切りが考慮されるかどうかは、rossi データセットを分析する際に使用される具体的なコードや手法に依存します。カプランマイヤー推定器を適用する際には、生存時間（week）とイベント発生インジケーター（通常は再逮捕されたかどうかを示すarrest）を使用し、これにより打ち切りデータが適切に扱われます。

b. コックス比例ハザードモデル

コックス比例ハザードモデルは、生存時間に影響を与える複数の共変量の効果を同時に評価するための半パラメトリックモデルです。

# コックス比例ハザードモデルのインスタンス化とフィット
cph = CoxPHFitter()
cph.fit(data, duration_col='week', event_col='arrest')

# モデルのサマリーの表示
cph.print_summary()

c. アクセラレーテッドフェイルアタイム（AFT）モデル

AFTモデルは、生存時間の対数が共変量の線形結合とパラメトリックな誤差項の和としてモデル化されるパラメトリックアプローチです。例としてワイブル分布を用いたAFTモデルを示します。

# AFTモデルのインスタンス化とフィット（ワイブル分布を使用）
aft = WeibullAFTFitter()
aft.fit(data, duration_col='week', event_col='arrest')

# モデルのサマリーの表示
aft.print_summary()

import numpy as np
import pandas as pd
from lifelines import KaplanMeierFitter, CoxPHFitter, WeibullAFTFitter
from lifelines.datasets import load_rossi
import matplotlib.pyplot as plt
# データセットの読み込み
data = load_rossi()
plt.hist(data.week)
plt.show()

# カプラン・マイヤー推定器のインスタンス化とフィット
kmf = KaplanMeierFitter()
kmf.fit(durations=data["week"], event_observed=data["arrest"])

# 生存関数のプロット
kmf.plot_survival_function()

生存関数$S(t)$は、特定の時間$t$までにイベント（この場合は再逮捕）が発生しない確率を示す関数です。

# コックス比例ハザードモデルのインスタンス化とフィット
cph = CoxPHFitter()
cph.fit(data, duration_col='week', event_col='arrest')

# モデルのサマリーの表示
cph.print_summary()
cph.plot()

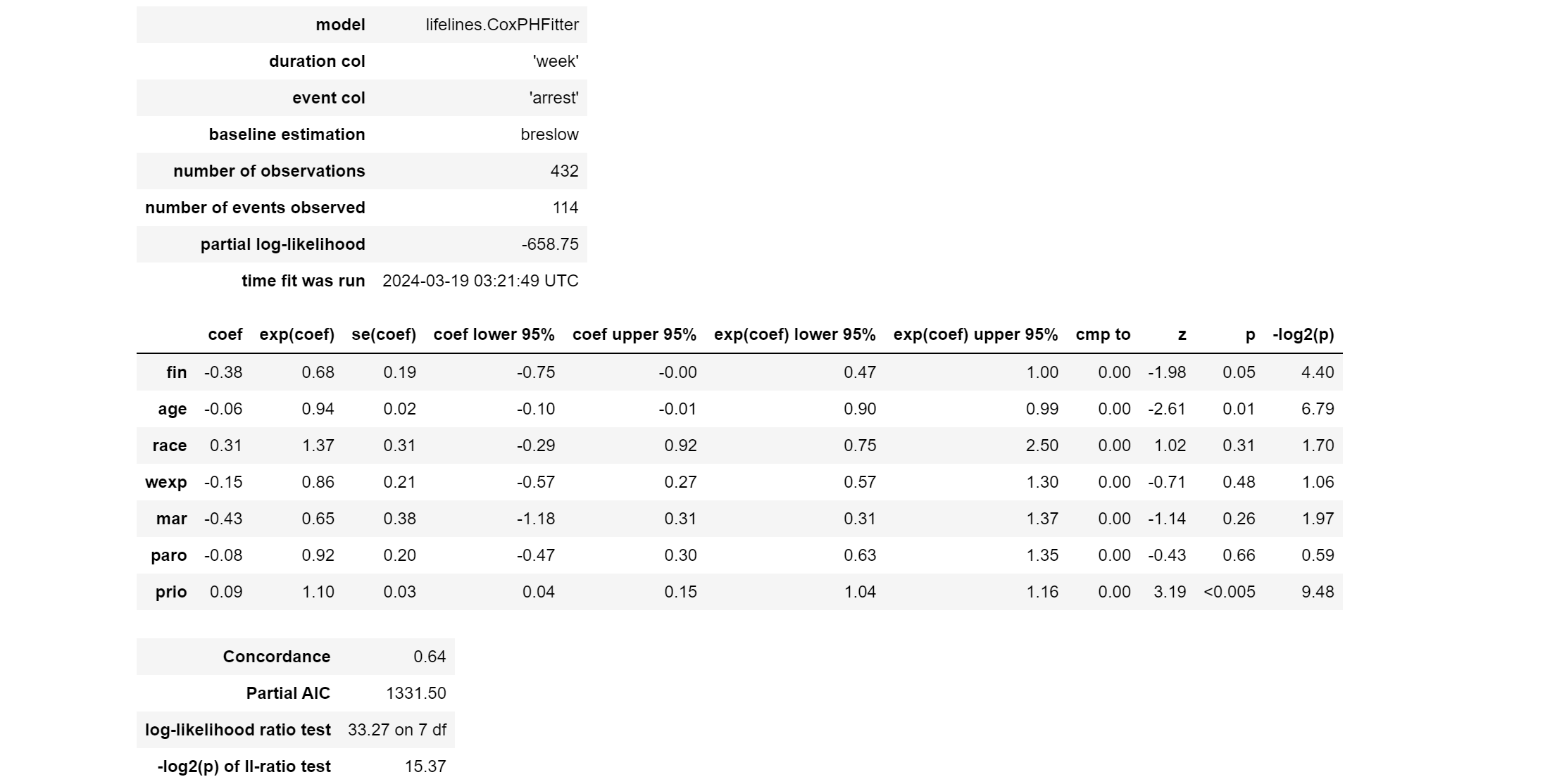
最初の表

• model: 使用されたモデルのクラス。この場合、lifelines.CoxPHFitterは、生存時間データに対してコックス比例ハザードモデルをフィッティングするために使用されます。

• duration col: 生存時間（またはフォローアップ時間）を含むデータフレーム内の列の名前。'week'は、被験者がイベント（再逮捕）を経験するまでの時間（週単位）を指します。

• event col: イベントの発生（この場合は再逮捕されたかどうか）を示すデータフレーム内の列の名前。'arrest'は、イベントが発生した（1）か発生していない（0）かを示します。

• baseline estimation: 基準ハザード関数を推定するために使用される方法。breslowは、Breslow法による基準ハザード関数の推定を示します。Breslow法は、部分尤度を最大化することにより、基準ハザード関数を推定する一般的な方法です。

• number of observations: 分析に含まれる観測（被験者）の総数。このケースでは、432の観測がモデルに含まれています。

• number of events observed: イベント（再逮捕）が観測された総数。この分析では、114のイベントが観測されました。

• partial log-likelihood: 部分尤度の対数値。モデルのフィットの良さを示す指標で、通常はモデル選択や比較に用いられます。このケースでは、-658.75となっています。部分対数尤度は、モデルのパラメーターが与えられたデータにどれだけ適合しているかを示す尺度で、値が大きい（絶対値が小さい）ほどモデルの適合が良いことを示します。ただし、単独での値の絶対値よりも、モデル間の比較においてその差が重要になります。

再逮捕までの時間（週）と再逮捕の発生に関する情報がモデリングされたことがわかります。また、432人の被験者のうち114人がイベントを経験しています。

２番目の表

各共変量がイベント発生のリスク（ハザード）に与える影響を定量的に評価しています。

• coef: 各共変量の回帰係数。正の値はイベントリスクの増加、負の値はリスクの減少を意味します。
• exp(coef): 回帰係数の指数関数（ハザード比）。1より大きい場合はリスクの増加、1より小さい場合はリスクの減少を意味します。
• se(coef): 回帰係数の標準誤差。
• coef lower 95% & coef upper 95%: 回帰係数の95%信頼区間。
• exp(coef) lower 95% & exp(coef) upper 95%: ハザード比の95%信頼区間。
• cmp to: 比較の基準点（この場合、出力には特に意味がありません）。
• z: zスコア。統計的検定における標準正規分布からの偏差を示します。
• p: p値。統計的有意性の尺度で、帰無仮説（ここでは共変量がリスクに影響を与えないという仮説）が真である確率を示します。
• -log2(p): p値の-log2変換。情報理論におけるビット単位の情報量を示します。

ー　各共変量の解釈

• fin: 財政支援を受けたことが再逮捕リスクを減少させることを示唆しています（ハザード比0.68、p=0.05）。
• age: 年齢が高いほど再逮捕リスクが若干減少することを示しています（ハザード比0.94、p=0.01）。
• race: 人種による有意なリスクの増加は見られません（ハザード比1.37、p=0.31）。
• wexp: 正式な雇用経験が再逮捕リスクの減少と関連していることを示唆していますが、統計的には有意ではありません（ハザード比0.86、p=0.48）。
• mar: 結婚していることが再逮捕リスクを減少させる可能性がありますが、これも統計的に有意ではありません（ハザード比0.65、p=0.26）。
• paro: 仮釈放状態が再逮捕リスクに有意な影響を与えないことを示しています（ハザード比0.92、p=0.66）。
• prio: 過去の逮捕回数が多いほど、再逮捕リスクが増加することが示されています（ハザード比1.10、p<0.005）。

この分析結果から、過去の逮捕回数（prio）が再逮捕リスクを顕著に増加させる主要なリスクファクターであることが示されています。一方で、財政支援を受ける（fin）や年齢が高い（age）ことは、リスクを低下させる可能性があることが示唆されています。ただし、他の共変量については、その影響が統計的に有意ではないか、またはリスクに対する影響が限定的であることが示されています。

一番下の表

コックス比例ハザードモデルのフィットの良さや統計的有意性に関する指標を提供しています：

• Concordance (C-index): 0.64。コンコーダンス指数（またはC指数）は、モデルの予測能力を評価する指標で、1に近いほど良い予測能力を示します。0.5はランダムな予測と同等であり、0.64はモデルがある程度予測能力を持つことを示していますが、完璧ではありません。この指標は、生存データのリスク予測におけるペアの比較の一致度を測定します。

• Partial AIC: 1331.50。部分的赤池情報量基準（AIC）は、モデルの適合度と複雑さのバランスを考慮した指標です。一般に、AICが小さいほど、適合度が良く、かつモデルが過度に複雑でないことを示します。ただし、AICは他のモデルとの比較においてのみ意味を持ち、単独での絶対値は直接的な解釈を持ちません。

• log-likelihood ratio test: 33.27 on 7 df（自由度）。対数尤度比検定は、モデルにおける共変量の全体的な統計的有意性を評価するために用います。ここでの値は、ヌルモデル（共変量がないモデル）と比較した場合の改善度を示しており、7つの自由度（モデルの共変量の数）に対して33.27という統計量が得られています。これはモデルが統計的に有意な改善を示していることを意味します。

• -log2(p) of ll-ratio test: 15.37。対数尤度比検定の結果から得られるp値の-log2変換です。この値が大きいほど、モデルの改善が統計的に有意であることを強く示唆しています。15.37は、非常に強い統計的有意性を示しています。

これらの指標は、モデルがデータに適合しており、共変量が再逮捕リスクの予測に有意な貢献をしていることを示しています。しかし、コンコーダンス指数からも分かるように、モデルの予測精度にはまだ改善の余地があることも示唆されています。

# AFTモデルのインスタンス化とフィット（ワイブル分布を使用）
aft = WeibullAFTFitter()
aft.fit(data, duration_col='week', event_col='arrest')

# モデルのサマリーの表示
aft.print_summary()
aft.plot()

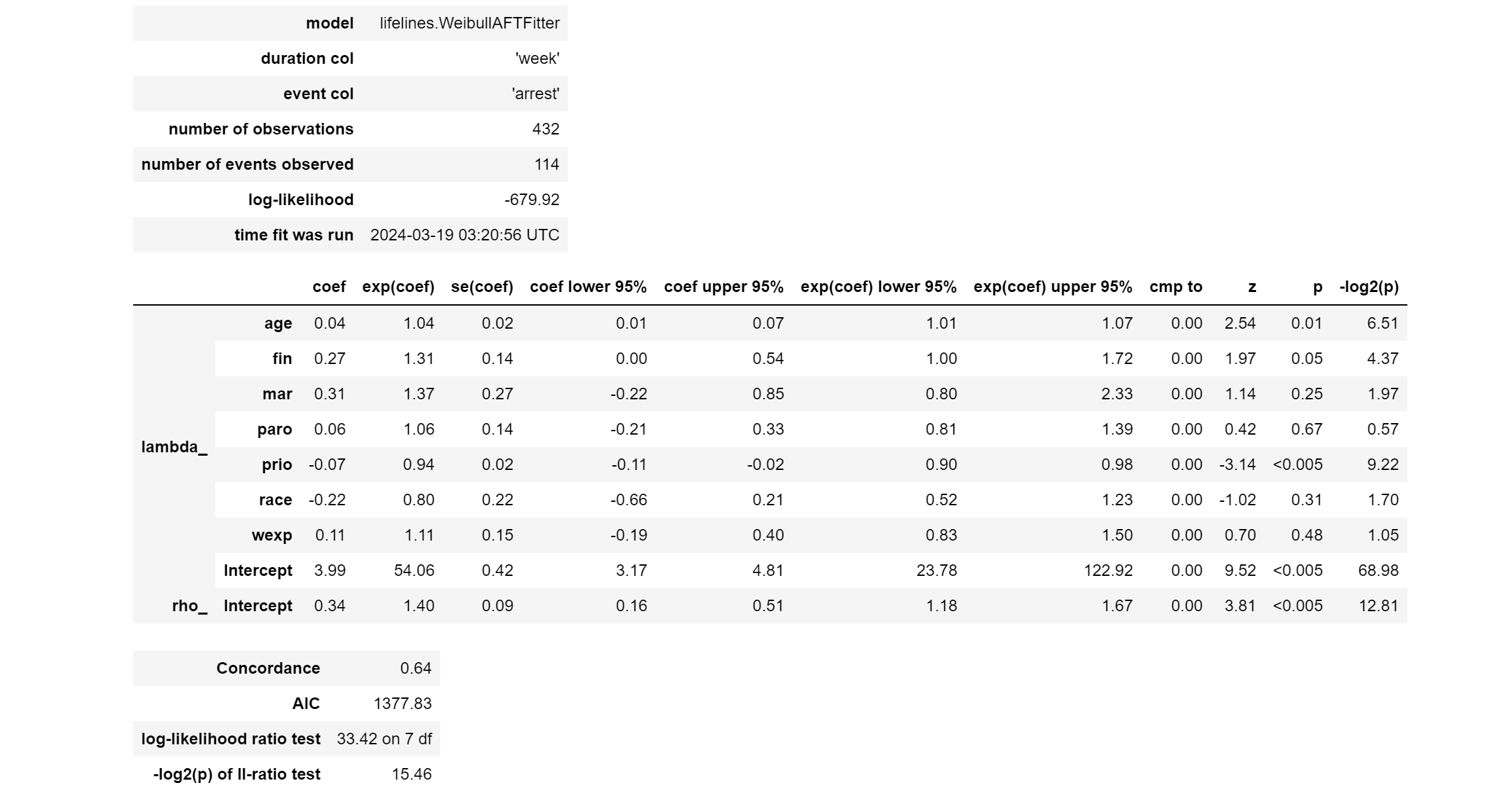
最初の表

アクセラレーテッドフェイルアタイム（AFT）モデルを適用しています。この場合、ワイブル分布が使用されています：

• model: 使用されたモデルの種類。lifelines.WeibullAFTFitterは、ワイブル分布を使用したAFTモデルのフィッティングを行うクラスです。

• duration col: 生存時間を含むデータフレーム内の列の名前。'week'は、被験者がイベント（この場合は再逮捕）を経験するまでの時間（週単位）を指します。

• event col: イベント発生（この場合は再逮捕されたかどうか）を示すデータフレーム内の列の名前。'arrest'は、イベントが発生したかどうかを示します（1が再逮捕、0が再逮捕されず）。

• number of observations: 分析に含まれる観測（被験者）の総数。このケースでは、432の観測がモデルに含まれています。

• number of events observed: イベント（再逮捕）が観測された総数。この分析では、114のイベントが観測されました。

• log-likelihood: モデルの対数尤度。これはモデルがデータにどれだけ適合しているかの尺度で、値が大きいほど（絶対値が小さいほど）データに適合していることを示します。この場合の値は-679.92です。

• time fit was run: モデルのフィットが実行された日時。ここでは2024年3月18日13時43分24秒（UTC）となっています。

２番目の表

• age (年齢): 係数が0.04で、exp(coef)が1.04です。これは、年齢が1単位増加するごとに、再逮捕までの時間が平均で約4%延長することを示しています。p値が0.01で統計的に有意であるため、年齢は再逮捕リスクに有意な影響を与える因子です。

• fin (財政支援): 係数が0.27で、exp(coef)が1.31です。財政支援を受けた個体は、受けていない個体に比べて再逮捕までの時間が平均で約31%延長することを示しています。p値が0.05で、この効果は統計的に有意です。

• mar (結婚しているか): 係数が0.31で、exp(coef)が1.37です。結婚していることが再逮捕までの時間を平均で約37%延長させる可能性がありますが、p値が0.25であり、この効果は統計的には有意ではありません。

• paro (仮釈放状態): 係数が0.06で、exp(coef)が1.06です。仮釈放状態の影響は比較的小さく、再逮捕までの時間に大きな影響を与えないことを示しています（p値0.67）。

• prio (過去の逮捕回数): 係数が-0.07で、exp(coef)が0.94です。過去の逮捕回数が多いほど、再逮捕までの時間が短縮することを示しており、1回の逮捕が加わるごとに再逮捕までの時間が平均で約6%短縮します。この効果は統計的に有意です（p<0.005）。

• race (人種): 係数が-0.22で、exp(coef)が0.80です。このモデルでは、人種が再逮捕までの時間に有意な影響を与えるとは限らないことを示しています（p値0.31）。

• wexp (正式な雇用経験): 係数が0.11で、exp(coef)が1.11です。正式な雇用経験が再逮捕までの時間を延長する可能性を示していますが、この影響は統計的に有意ではありません（p値0.48）。

• Intercept (切片): 生存時間の基準となるスケールを表します。lambda_の切片は3.99であり、これはモデルの基準となる生存時間のスケールを示しています。

• rho_ (Intercept): ワイブル分布の形状パラメーターに関連する切片です。0.34の値は、生存時間分布の形状を示しており、再逮捕までの時間の分布がどのような形状をしているかを表します。このパラメーターは再逮捕リスクの時間依存性を捉えています。

一番下の表

アクセラレーテッドフェイルアタイム（AFT）モデルの性能評価に関する指標を示しています：

• Concordance (C-index): 0.64。コンコーダンス指数は、モデルの予測能力を示す指標で、値が1に近いほど予測性能が高いことを意味します。0.64は、モデルがある程度の予測能力を持つことを示していますが、予測精度の改善の余地があることも示唆しています。

• AIC (赤池情報量基準): 1377.83。AICは、モデルの適合度と複雑さのトレードオフを考慮した指標で、値が小さいほど良いモデルであるとされます。他のモデルと比較することにより、相対的なモデルの適合度を評価することができます。

• log-likelihood ratio test: 33.42 on 7 df。対数尤度比検定は、モデルの共変量が統計的に有意な寄与をしているかを評価するテストで、7つの自由度（モデルに含まれる共変量の数）に対して33.42の統計量が得られました。これは、モデルが統計的に有意な情報を提供していることを示しています。

• -log2(p) of ll-ratio test: 15.46。対数尤度比検定の結果から得られるp値を-log2変換した値です。この変換は、結果の有意性をビット単位で表すことを目的としており、値が大きいほどモデルの統計的有意性が高いことを示します。15.46という値は、モデルの共変量が再逮捕時間に対して非常に有意な影響を与えていることを示しています。

これらの結果から、AFTモデルがrossiデータセットに対して適合しており、共変量が再逮捕までの時間に統計的に有意な影響を与えていることが示されています。コンコーダンス指数からは、モデルの予測性能に改善の余地があることが示唆されていますが、モデルの共変量は再逮捕リスクの予測に有意な情報を提供していることが確認できます。

７．相互作用、競合効果への対策：サブディストリビューションハザードモデル

a. サブディストリビューションハザードモデル

サブディストリビューションハザードモデルは、特に競合リスクの存在下での生存時間データを分析する際に用いられる統計モデルです。競合リスクとは、研究中の特定のイベント以外の原因で終了するケースを指し、これによりイベントのリスク評価が複雑になります。サブディストリビューションハザードモデルは、これら競合リスクの一つが発生するリスクを直接モデル化します。

このモデルの一般的な形式は、ファイン＆グレイモデルとして知られており、競合リスクの存在下で特定のイベントに焦点を当てた時間までのリスク（ハザード）を推定します。ファイン＆グレイモデルは、コックス比例ハザードモデルを拡張した形であり、特定のイベントのサブディストリビューションハザード関数を推定するために使用されます。

ーファイン＆グレイモデル

ファイン＆グレイモデルでは、特定のイベントのサブディストリビューションハザード $h^*(t)$ は次のように表されます：

$$ h^*(t) = \lim_{dt \to 0} \frac{P(t \leq T < t + dt, \text{イベント発生} | T \geq t, \text{イベント未発生})}{dt} $$

ここで、$T$ は時間を、$h^*(t)$ は時間 $t$ における特定のイベント発生のサブディストリビューションハザードを示します。

このモデルは、他の原因によるイベント発生を競合リスクとして考慮し、研究対象のイベントに特化したリスク推定を可能にします。したがって、特定のイベントのリスクを他のリスクの影響から分離して評価することができるため、競合リスクが存在する場合の生存時間データ分析において有用です。

ー応用

サブディストリビューションハザードモデルは、医療研究において複数の疾患や治療の影響を受ける可能性がある患者の生存分析、または工学における複数の故障原因を持つシステムの信頼性分析など、さまざまな分野で応用されています。このモデルを用いることで、特定のイベントに対するリスク要因の影響をより正確に評価し、適切な予防策や治療戦略の策定に役立てることができます。

ー　rossiへの適応

データをエピソード形式に変換することは、特に時間依存の共変量を扱う場合や、より複雑なモデルを構築する際に有用です。エピソード形式に変換することで、各被験者の観察期間を複数のサブ期間（エピソード）に分割し、時間経過に伴う共変量の変化や状態の変化をより詳細に反映させることが可能になります。

1. 対象の列を選択: target_colsを定義することで、分析に含める変数を選択しています。これにより、モデルに必要なデータのみを含むデータフレームを作成しています。

2. エピソード形式への変換: to_episodic_format関数を使用して、元のデータフレームをエピソード形式に変換しています。この手法は、生存時間分析で共変量の時間変化を考慮する場合に特に有用です。duration_colには生存時間を示す列名を、event_colにはイベント発生（ここでは再逮捕）を示す列名を指定しています。time_gaps=1.は、エピソード間の時間間隔を指定しており、このケースでは1週間ごとにエピソードを分割しています。

rossiデータセットにおいては、元のデータが時間依存の共変量を含まないため、全ての共変量が時間経過によって変化しない静的な共変量です。エピソード形式への変換は、共変量が時間によって変化する（例えば、仮釈放状態が時間とともに変わる、経済状況が変化するなど）場合に特に有用です。この変換はデモ目的です。

target_cols = ['week', 'arrest', 'fin', 'age', 'race', 'wexp', 'mar', 'paro', 'prio']
model_df = data.loc[:, target_cols]

# エピソード分割
from lifelines.utils import to_episodic_format

model_df_episode = to_episodic_format(model_df, duration_col='week', 
    event_col='arrest', time_gaps=1.)

model_df_episode.head()

from lifelines import CoxTimeVaryingFitter
ctv = CoxTimeVaryingFitter()

ctv.fit(
    model_df_episode,id_col='id',event_col='arrest',start_col='start',
    stop_col='stop',)
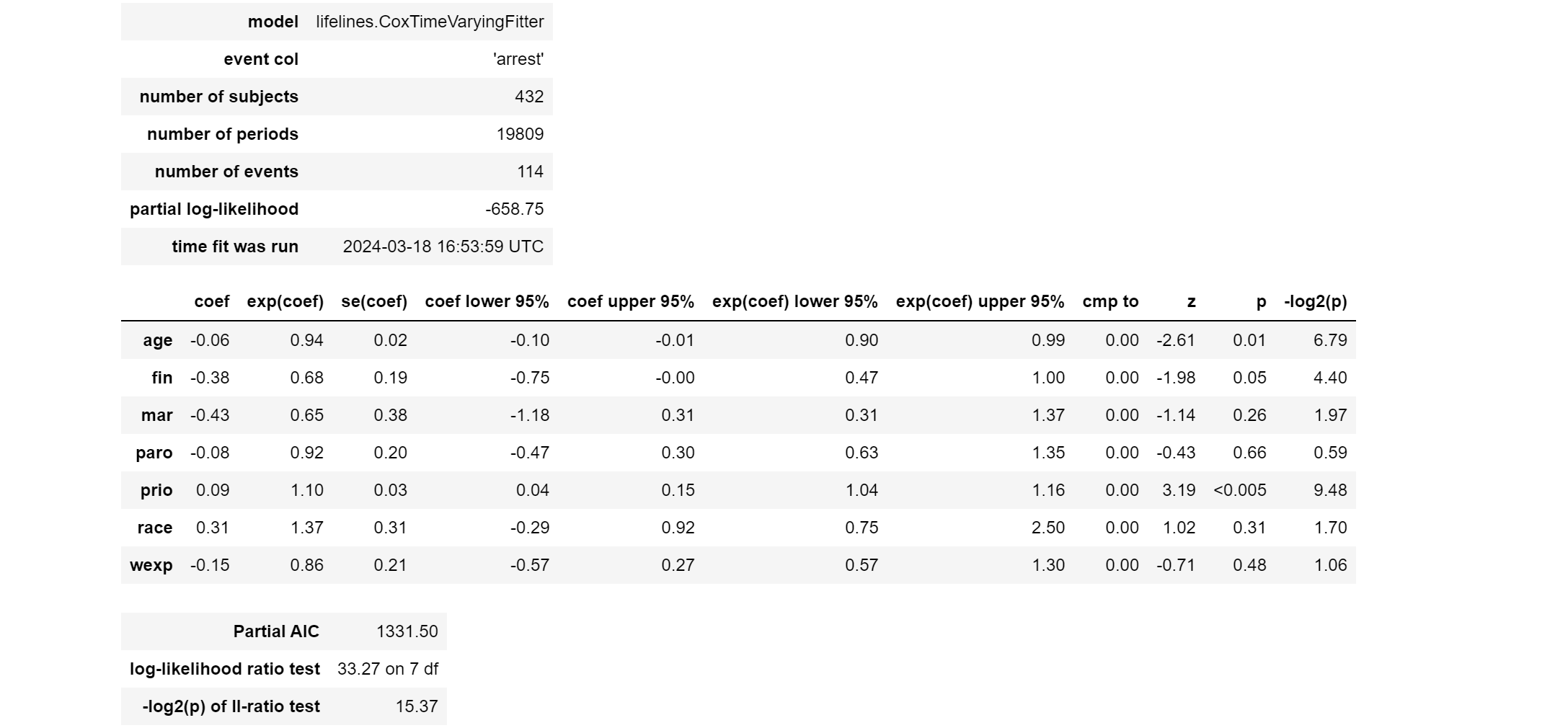
ctv.print_summary()
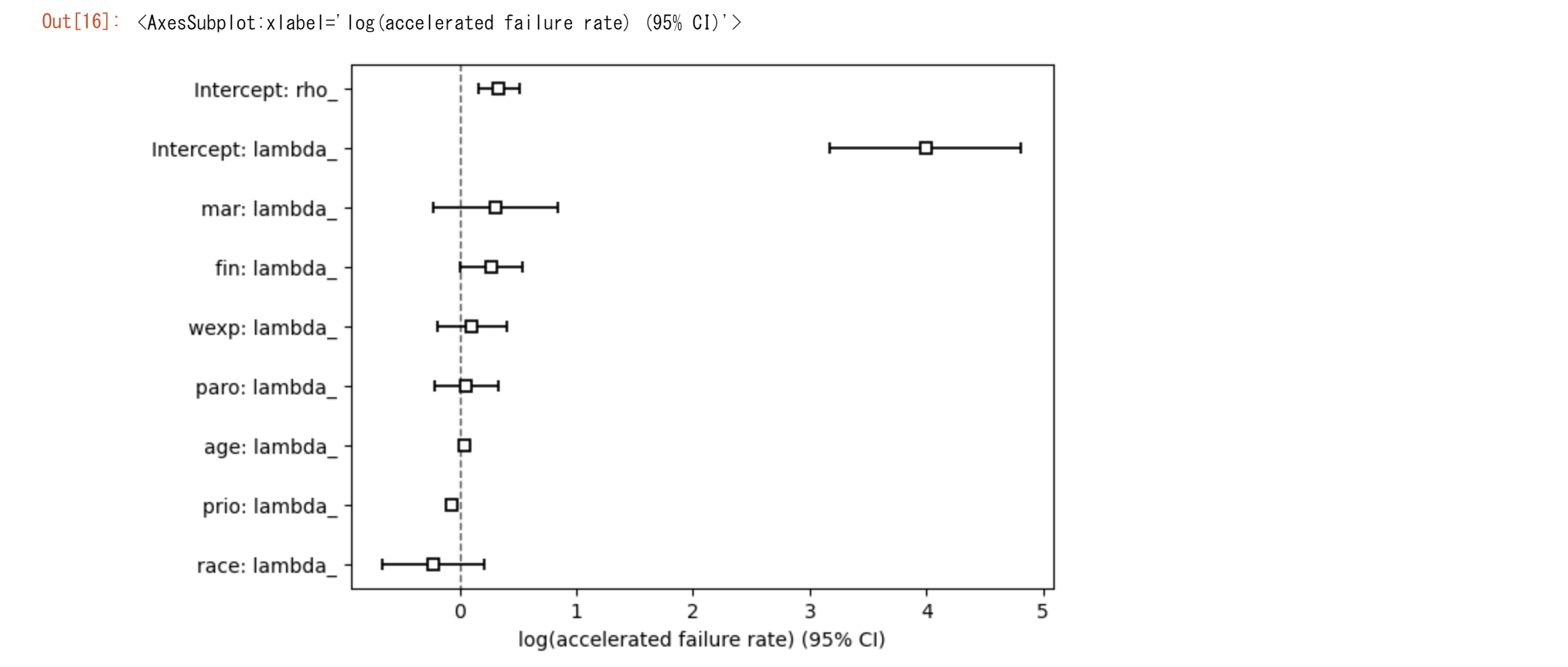
ctv.plot()

最初の表

• model: 使用されたモデルの種類。lifelines.CoxTimeVaryingFitterは、時間変動共変量を扱うことができるコックス比例ハザードモデルです。

• event col: イベントの発生（この場合は再逮捕されたかどうか）を示すデータフレーム内の列の名前。'arrest'は、イベントが発生した（1）か発生していない（0）かを示します。

• number of subjects: 分析に含まれる被験者（主体）の総数。このケースでは、432人の被験者が分析に含まれています。

• number of periods: 分析における総期間（エピソード）の数。この場合、19,809の異なる期間がモデルに含まれています。これは、時間変動共変量を考慮するため、各被験者のデータが複数の期間に分割されていることを示しています。

• number of events: イベント（再逮捕）が観測された総数。この分析では、114のイベントが観測されました。

• partial log-likelihood: モデルの部分対数尤度。この値はモデルがデータにどれだけ適合しているかの尺度で、この場合-658.75です。部分対数尤度は、モデルのパラメーターが与えられたデータにどれだけよく適合しているかを示します。値自体よりも、モデル間の比較におけるこの値の相対的な大きさが重要です。

• time fit was run: モデルのフィットが実行された日時。2024年3月18日14時27分38秒（UTC）となっています。

２番目の表

• age (年齢): 係数が-0.06で、exp(coef)が0.94です。これは、年齢が1年増えるごとに、再逮捕までの時間が長くなる（リスクが6%減少する）ことを意味します。統計的に有意であり（p=0.01）、年齢が再逮捕リスクに負の影響を与えることを示しています。

• fin (財政支援): 係数が-0.38で、exp(coef)が0.68です。財政支援を受けた個体は、受けていない個体に比べて再逮捕リスクが32%低いことを示しており、これも統計的に有意です（p=0.05）。

• mar (結婚しているか): 係数が-0.43で、exp(coef)が0.65です。結婚していることが再逮捕リスクを35%減少させる可能性がありますが、この効果は統計的に有意ではありません（p=0.26）。

• paro (仮釈放状態): 係数が-0.08で、exp(coef)が0.92です。仮釈放状態の影響は小さく、再逮捕までの時間に有意な影響を与えないことを示しています（p=0.66）。

• prio (過去の逮捕回数): 係数が0.09で、exp(coef)が1.10です。過去の逮捕回数が多いほど、再逮捕リスクが増加する（10%増加する）ことを示しており、この効果は統計的に有意です（p<0.005）。

• race (人種): 係数が0.31で、exp(coef)が1.37です。人種が再逮捕リスクに与える影響は統計的に有意ではありません（p=0.31）が、黒人であることがリスクを37%増加させる可能性を示唆しています。

• wexp (正式な雇用経験): 係数が-0.15で、exp(coef)が0.86です。正式な雇用経験があることが再逮捕リスクを14%減少させる可能性がありますが、この効果は統計的に有意ではありません（p=0.48）。

これらの結果から、特に年齢や財政支援、過去の逮捕回数が再逮捕までの時間に重要な影響を与えていることがわかります。

一番下の表

• Partial AIC (赤池情報量基準): 1331.50。AICは、モデルの適合度と複雑さのバランスを示す指標で、値が小さいほど良いモデルであるとされます。部分的赤池情報量基準（Partial AIC）は、特に大規模なデータセットや複雑なモデルにおいて計算されることが多く、モデル選択に役立ちます。

• log-likelihood ratio test: 33.27 on 7 df。対数尤度比検定は、モデルが含む共変量が統計的に有意な情報を持っているかを検定します。ここでの値は、ヌルモデル（共変量がないモデル）と比較して、含まれる共変量がモデルの適合度をどの程度改善しているかを示しています。7つの自由度は、モデルに含まれる共変量の数を表しており、統計量が33.27という値は、共変量がモデルに有意な情報を加えていることを示しています。

• -log2(p) of ll-ratio test: 15.37。これは、対数尤度比検定の結果から得られるp値を-log2変換したもので、結果の有意性をビット単位で示しています。値が大きいほど、共変量がモデルに与える影響の統計的有意性が高いことを意味します。15.37という値は、共変量がモデルの適合度に非常に有意な影響を与えていることを示しています。

これらの統計的指標は、時間変動共変量を考慮したモデルがrossiデータセットに適合しており、共変量が再逮捕までの時間（生存時間）に対して統計的に有意な影響を与えていることを示しています。特に、対数尤度比検定とその-p変換からの結果は、モデルの共変量が再逮捕リスクを説明する上で重要な役割を果たしていることを強く示唆しています。

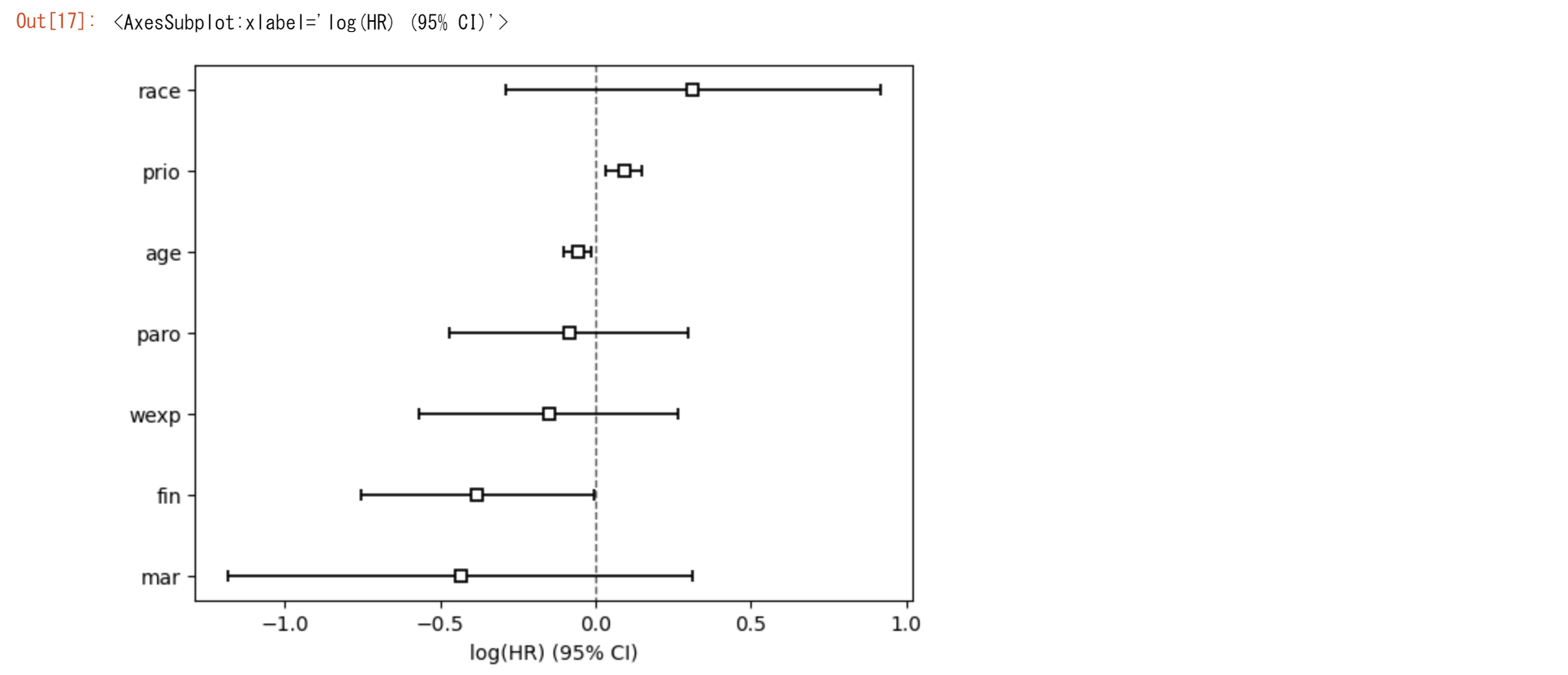
プロットの解釈

1. ハザード比の推定値と信頼区間: ctv.plot()は、モデルに含まれる各共変量に対して、ハザード比（exp(coef)）の推定値とその95%信頼区間をプロットします。ハザード比は、特定の共変量の値が1単位増加したときのイベント発生率の相対的な変化を示します。プロット上では、各共変量に対するハザード比の推定値が点で、信頼区間が線で示されます。

2. 共変量の影響の方向: ハザード比が1より大きい場合（プロット上で縦の破線が1を超える位置に点がある場合）、その共変量がイベント発生のリスクを増加させることを意味します。ハザード比が1より小さい場合は、リスクを減少させることを意味します。

3. 統計的有意性: 信頼区間が1を含む場合（信頼区間の線が縦の破線の1を跨いでいる場合）、その共変量の影響は統計的に有意ではないと解釈されます。逆に、信頼区間が1を含まない場合、共変量の影響は統計的に有意です。

4. 共変量間の比較: プロットを通じて、共変量間でハザード比の大きさや方向、統計的有意性を比較することができます。これにより、イベント発生のリスクに最も強い影響を与える共変量を特定することが可能になります。

図からageとfinが有意であることが分かります。

Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。