採択・棄却法が今一歩よくわからないので、いろいろ試してみました。メモとして残します。
ー乱数生成採択棄却法ー
採択・棄却法とは, 任意の確率密度関数 $f(x)$ からサンプルを生成するために、提案分布と呼ばれる別のより扱いやすい確率密度関数$g(x)$を用いる方法である。この方法では、$g(x)$ から得られたサンプルが、目標分布$f(x)$ にどの程度適合しているかを評価し、適切なサンプルのみを採択して、$f(x)$ のサンプルとする。
$g(x)$と一様乱数$u$を利用して$f(x)$を密度にもつ確率変数$X$の乱数が生成
できる.
1.$g(x)$から乱数$x$と$U(0,1)$から一様乱数$u$をとる.
2.$r=l(x)/(Mg(x))$として$u\le r$ならば$x$を出力し,そうでないならば1.に戻る.
$g(x)$から$x$を生成し、それとは独立に一様乱数$u$を生成して、$f(x)$を密度にもつ確率変数$X$を生成する。その過程で用いられる$l(x)$は$f(x)$と$l(x)/c=f(x)$の関係にあり、$c$は正規化定数だが、$l(x)$自体が$f(x)$の一部というわけではない。それらは、比例関係にあればよい。ただし、$g(x)$が生成する$x$は、$f(x)$の$x$の値のサポート(上限から下限)をカバーしてい無ければならない。
$f(x)$は確率密度関数なのでその積分値は1になる。また$f(x)$はゼロより大きく、1を超えることもある。$g(x)$が$f(x)$の確率密度のすべてをカバーできていなければ、確率関数$f(x)$を実現することはできない。よって、$Mg(x)>=l(x)$を仮定する。
$Mg(x)>=l(x)$の両辺を$Mg(x)$で割れば、$1>=l(x)/(Mg(x))$であり、右辺を$r$と置けば、$r$はゼロから1の間の値を取る。$l(x)$が小さければ、$r$も小さく、$l(x)$が大きければ1に近づく可能性がある。$x$は$g(x)$から得られているので$l(x)$を$g(x)$で割ることは、$f(x)$を$g(x)$から得られた$x$に限定していることを意味し、$r$は最終的に採択率に収束する。
$g(x)$から生成される$x$は$g(x)$が$f(x)$と完全に一致していれば、$x$はすべて受け入れられるべきである。そうするためには$M$は小さければよい。一方で、$g(x)$が$f(x)$と完全に一致していなくても、$x$を適切に選択することで$f(x)$を実現できる。その目安が$M$であり、$r$である。$r$は$f$に比例しているので、$r$が大きいときにより多くの$x$を採択し、小さいときには採択を少なくしなければならない。しかし、これを実現するのは容易ではない。なぜなら$l(x)$は$f(x)$自体ではないので、大数の法則のように多くの試行で収束するとは限らないからである。そこで一様乱数$u$を生成する。$u$は0と1の間で均等に発生するのであるから、これを確率と見ることができる。この$u$を$r$と比べることで$u$を上回る$r$の$x$を採択すれば、$u$より高い確率で生じる$x$を多く採択することができる。
まず3つのタイプを調べてみよう。
1.$g$と$f$の確率密度関数が同じ。$l$により$r$の算出
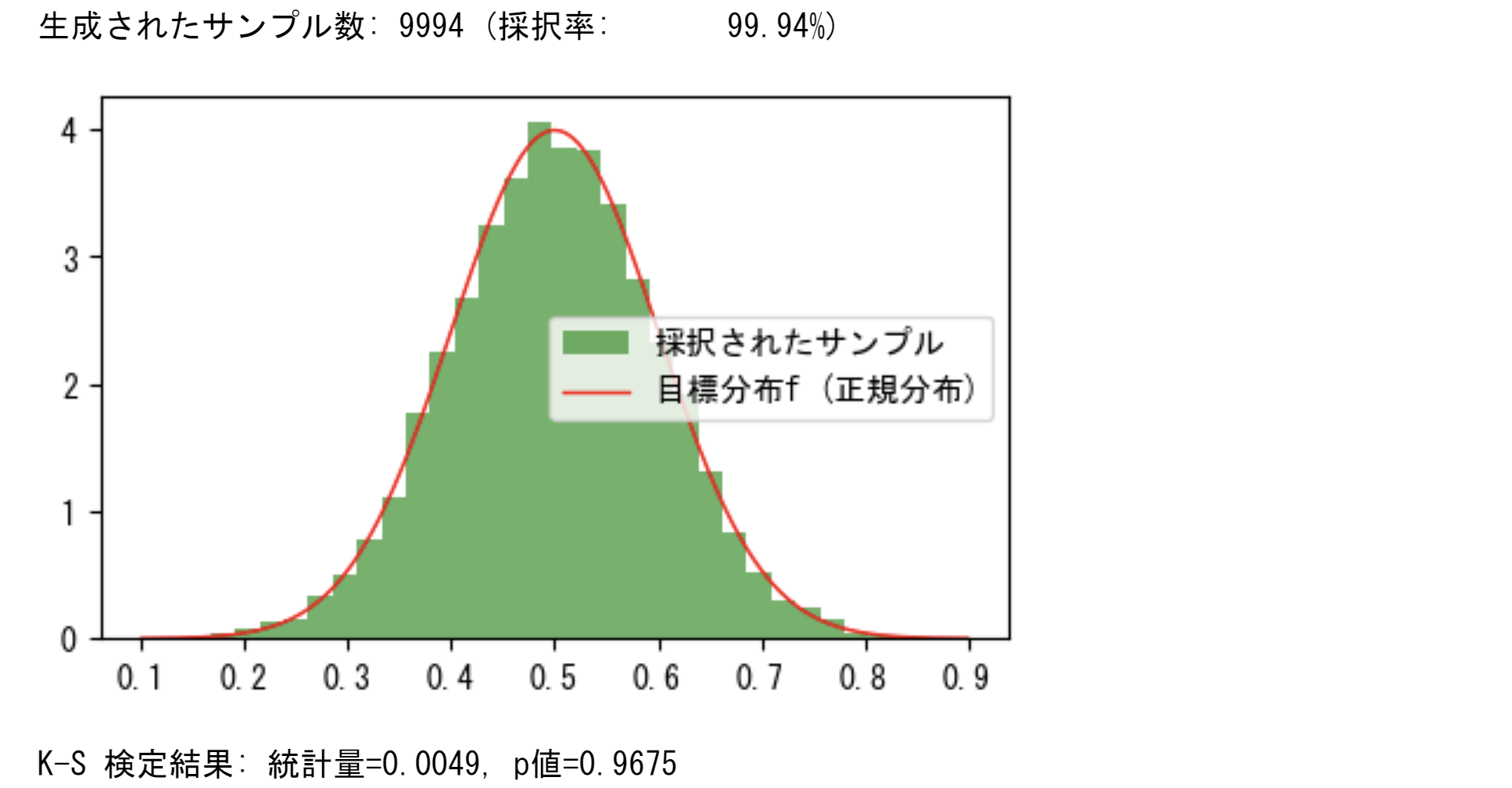
すべての$x$を採択するために$r=1$としたい。そのために$M=0.001$とする。
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = "MS Gothic"
from scipy.stats import norm, uniform
import scipy.stats as stats
# パラメータ設定
n_samples = 10000 # 生成するサンプルの総数
M = 0.001 # 適切なMの値を選択
mu_f = 0.5 # 目標分布fの平均
sigma_f = 0.1 # 目標分布fの標準偏差
# 提案分布gからのサンプル生成
g_samples = np.random.normal(mu_f,sigma_f, n_samples)
# 一様乱数の生成
u = np.random.uniform(0, 1, n_samples)
# サンプリング実行
# 採択・棄却プロセス
accepted_samples = []
for i in range(n_samples):
x = g_samples[i]
# f(x)とg(x)の確率密度関数の値を計算
l_x=np.exp(-(x-mu_f)**2/sigma_f**2)
g_x = norm.pdf(x,mu_f,sigma_f)
# 採択・棄却条件
if u[i] <= l_x/ (M * g_x):
accepted_samples.append(x)
# 結果の表示
print(f"生成されたサンプル数: {len(accepted_samples)} (採択率: \
{len(accepted_samples) / n_samples * 100:.2f}%)")
# 結果の可視化
plt.figure(figsize=(5, 3))
plt.hist(accepted_samples, bins=30, density=True, alpha=0.6, color='g', \
label='採択されたサンプル')
# 目標分布f(正規分布)の確率密度関数をプロット
x = np.linspace(mu_f - 4*sigma_f, mu_f + 4*sigma_f, 1000)
plt.plot(x, norm.pdf(x, mu_f, sigma_f), 'r-', lw=1, label='目標分布f (正規分布)')
plt.legend()
plt.show()
norm.pdf(0.5, mu_f, sigma_f)
# コルモゴロフ-スミルノフ検定
ks_stat, ks_pvalue = stats.kstest(accepted_samples, 'norm', args=(mu_f, sigma_f))
print(f"K-S 検定結果: 統計量={ks_stat:.4f}, p値={ks_pvalue:.4f}")
採択率は99%を超え、K-S検定のp値は0.96を超える。
2.$g$は一様分布[0,1],$r$は$f$により算出
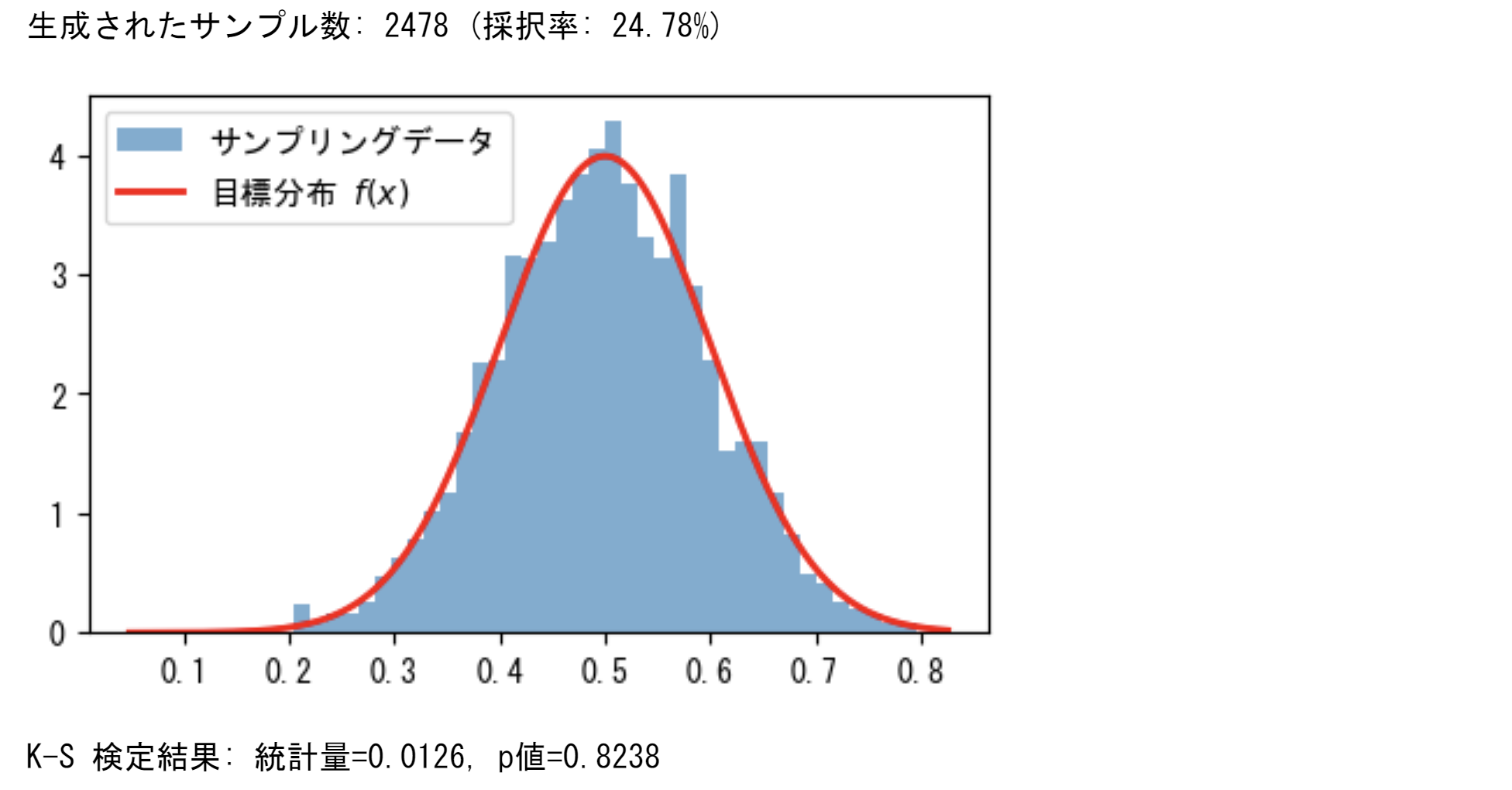
その場合、[0,1]の一様分布の確率密度は1なので、1より大きなfには対処できない。なぜならfが1より大きくなる$x$、つまり$r\ge u$をすべて受け入れても$r=1$となる頻度の数が足らなくなるからである。$M=1$とするとfの確率密度の平均近辺の頻度が足らなくなってしまう。$x=0.5$のときにfの確率密度は最大のとなり3.99であるので、$M=4$とすれば、$r$は$x=0.5$で最大となる。
# パラメータ設定
M = 4 # 適切なMの値を選択
# 提案分布gからのサンプル生成
g_samples = np.random.uniform(0,1, n_samples)
# 一様乱数の生成
u = np.random.uniform(0, 1, n_samples)
# サンプリング実行
# 採択・棄却プロセス
accepted_samples = []
for i in range(n_samples):
x = g_samples[i]
# f(x)とg(x)の確率密度関数の値を計算
f_x = norm.pdf(x, mu_f, sigma_f)
g_x = uniform.pdf(x)
# 採択・棄却条件
if u[i] <= f_x / (M * g_x):
accepted_samples.append(x)
# 結果の表示
print(f"生成されたサンプル数: {len(accepted_samples)}\
(採択率: {len(accepted_samples) / n_samples * 100:.2f}%)")
# 結果の可視化
plt.figure(figsize=(5, 3))
plt.hist(accepted_samples, bins=50, density=True, alpha=0.6\
, label='サンプリングデータ')
x = np.linspace(min(accepted_samples), max(accepted_samples), 1000)
plt.plot(x, stats.norm.pdf(x, mu_f, sigma_f), 'r-', lw=2, label='目標分布 $f(x)$')
plt.legend()
plt.show()
# コルモゴロフ-スミルノフ検定
ks_stat, ks_pvalue = stats.kstest(accepted_samples, 'norm', args=(mu_f, sigma_f))
print(f"K-S 検定結果: 統計量={ks_stat:.4f}, p値={ks_pvalue:.4f}")
採択率は25%に近く、K-S検定のp値は0.80を超える。
3. $g$は一様分布[0,1], $r$は$l$により算出
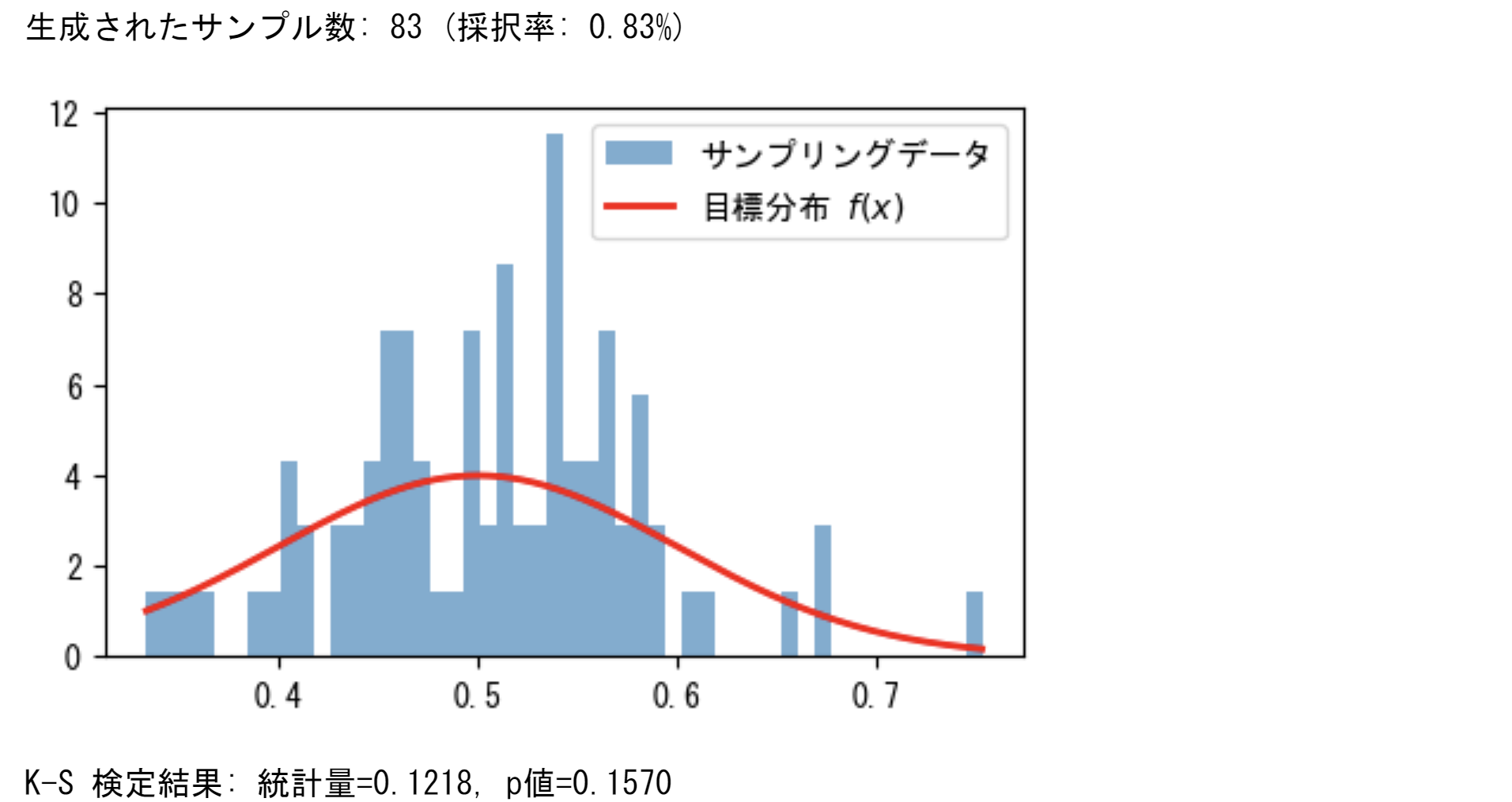
その場合、[0,1]の一様分布の確率密度は1なので、1より大きなfには対処できない。なぜならfが1より大きくなる$x$、つまり$r\ge u$をすべて受け入れても$r=1$となる頻度の数が足らなくなるからである。$M=20$とすれば、$r$は$x=0.5$で最大となる。
# パラメータ設定
n_samples = 10000 # 生成するサンプルの総数
M = 20 # 適切なMの値を選択
# 提案分布gからのサンプル生成
g_samples = np.random.uniform(0,1, n_samples)
# 一様乱数の生成
u = np.random.uniform(0, 1, n_samples)
# サンプリング実行
# 採択・棄却プロセス
accepted_samples = []
for i in range(n_samples):
x = g_samples[i]
# f(x)とg(x)の確率密度関数の値を計算
l_x=np.exp(-(x-mu_f)**2/sigma_f**2)
g_x = uniform.pdf(x)
# 採択・棄却条件
if u[i] <= l_x / (M * g_x):
accepted_samples.append(x)
# 結果の表示
print(f"生成されたサンプル数: {len(accepted_samples)} \
(採択率: {len(accepted_samples) / n_samples * 100:.2f}%)")
# 結果の可視化
plt.figure(figsize=(5, 3))
plt.hist(accepted_samples, bins=50, density=True, alpha=0.6\
, label='サンプリングデータ')
x = np.linspace(min(accepted_samples), max(accepted_samples), 1000)
plt.plot(x, stats.norm.pdf(x, mu_f, sigma_f), 'r-', lw=2, label='目標分布 $f(x)$')
plt.legend()
plt.show()
# コルモゴロフ-スミルノフ検定
ks_stat, ks_pvalue = stats.kstest(accepted_samples, 'norm', args=(mu_f, sigma_f))
print(f"K-S 検定結果: 統計量={ks_stat:.4f}, p値={ks_pvalue:.4f}")
採択率は1%未満であり、K-S検定のp値は約0.15であるが、結果は$M$の値に敏感である。
1,2,3の結果によりgをfとしrをfで計算すれば理想的でありが、それができなければrをlで計算し、できる限りgをfに近づけることが重要である。
このような理解のもと、採択・棄却法は、目標分布の正確な形を完全には知らない状況でも、その分布からのサンプリングを効果的に模倣するために広く用いられています
まとめると次に様に表現できる。
指示関数$I$を, $x$が採択されたら$I(x)=1$, 採択されなかったら$I(x)=0$をとると定義する.
$$P(I=1)=\int P(I=1|X=x)g(x)dx=\int \frac{cf(x)}{Mg(x)}g(x)dx=\frac{c}{M}$$
そうすると, $I(x)=1$での$x$の条件付き確率密度関数$p(x|I=1)$は, $f(x)$に等しい.
$$p(x|I=1)=\frac{P(I(x)=1|x)g(x)}{P(I=1)}=\frac{cf(x)}{Mg(x)}/P(I=1)=f(x)$$
Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。