Python3ではじめるシステムトレード：ヤコビアン

2023/7/25 13:30
ヤコビアンは統計学実践ワークブックの４章変数変換に出てきますが、限られたページ数の中での説明なので、よくわかりません。そこで英語のウィキ

https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant
を基にPythonコードを含めて、調べてみました。DeepL,ChatGPTと使っています。

いつも通り間違いがあると思うので、ご指摘いただければ幸いです。

これは「データの分析方法を学ぶ会」の勉強会で悩んだ問題の１つです。定期的に勉強会を開いています。https://study-data-analysis.connpass.com/

関数$f :\mathbb{R}^n → \mathbb{R}^m$ は、その一階偏導関数が$\mathbb{R}^n$ 上で存在するとします。このとき、$f$のヤコビアン行列はm×nの行列であり、$(i,j)$番目の要素は$\mathbf{J}_{ij}=\frac{\partial f_i}{\partial x_j}$ であると定義されます。

\mathbf{J}=\left[\frac{\partial \mathbf{f}}{\partial x_1},\cdots, \frac{\partial \mathbf{f}}{\partial x_n}\right]
=
\begin{bmatrix}
\nabla^Tf_1 \\
\vdots \\
\nabla^Tf_m
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial f_1}{\partial x_1}&,\cdots,&\frac{\partial f_1}{\partial x_n}\\
\vdots & \ddots &\vdots \\
\frac{\partial f_m}{\partial x_1}&,\cdots,&\frac{\partial f_m}{\partial x_n}
\end{bmatrix}

ここで $\nabla^Tf_i$ は、i成分の勾配の転置（行ベクトル）です。

ヤコビアン行列は、$f$が微分可能なすべての点で$f$の微分を表します。詳しくは、もし$h$が列行列で表される変位ベクトルであるなら、行列積$\mathbf{J}(x)・h$も別の変位ベクトルであり、それは$f(x)$が$x$で微分可能である場合、$x$の近傍で$f$の変化の最良の線形近似となります。

$m=n$のとき、ヤコビアン行列は正方形になり、その行列式は$x$の関数としてよく定義され、これは$f$のヤコビアン行列式として知られています。ヤコビアン行列式は、多重積分の変数変換時にも現れます。

$m=1$のとき、つまり$f: \mathbb{R}^n → \mathbb{R}$がスカラー値関数であるとき、ヤコビアン行列は行ベクトル $\nabla^{\mathrm{T}}f$ に簡略化されます。つまり、$\mathbf{J}_f = \nabla^Tf$ です。

複数変数を持つベクトル値関数のヤコビアンは、複数変数を持つスカラー値関数の勾配を一般化したものであり、これはさらに単一変数のスカラー値関数の導関数を一般化したものです。関数が微分可能な各点において、そのヤコビアン行列は、その点の近くで関数が局所的に課す「伸び」、「回転」、または「変換」の量としても理解することができます。

ヤコビアンは多重積分、特に2重積分における変数変換においても非常に重要な役割を果たします。この修正はヤコビアン（この場合はヤコビアン行列式、すなわちヤコビアン行列の行列式）を使用して行われます。

関数がある点で微分可能である場合、その微分はヤコビアン行列によって座標で与えられます。関数がヤコビアン行列を定義するために微分可能である必要はありません。なぜなら、存在が必要なのはその一階偏導関数のみだからです。

もし関数$f$が$\mathbb{R}^n$の点$p$で微分可能であるとき、その微分は$\mathbf{J}{\mathbf{f}}(\mathrm{p})$で表されます。このとき、$\mathbf{J}{\mathbf{f}}(\mathrm{p})$で表される線形変換は、点$p$付近での$f$の最良の線形近似となります。

合成可能な可微分関数$f:\mathbb{R}^n → \mathbb{R}^m$ と $g:\mathbb{R}^m → \mathbb{R}^k$は連鎖律を満たします。すなわち、

$$\mathbf {J} _{\mathbf {g} \circ \mathbf {f} }(\mathbf {x} )=\mathbf {J} _{\mathbf {g} }(\mathbf {f} (\mathbf {x} ))\mathbf {J} _{\mathbf {f} }(\mathbf {x} )$$

(x)が$\mathbb{R}^n$内の$x$について成り立ちます。

なぜヤコビアンが必要か

ヤコビアンが必要になる理由はもともと$n$次元の直交座標上にあった変数を別の変数に変数変換した際にある新しい変数を１つ動かすともともとの座標系全体が動いてしまうからで、それの微小変化を見た際に前と後での面積の違いを表現しているわけです。具体的には、新しい座標系における微小領域の面積（または体積）と、その対応する元の座標系における面積（または体積）との比を与えます。これが、ヤコビアンが変数変換の「伸び」や「回転」を考慮に入れる役割を果たす理由です。

もう少し具体的に説明するために、2次元の例を考えてみましょう。ある点(x, y)を中心とした微小領域dx dyと、それに対応する新しい座標系(u, v)における微小領域du dvを考えます。変数変換が行われると、一般に微小領域dx dyは一種の「変形」を受け、面積が変わることがあります。

この変形の程度を表すのがヤコビアンです。ヤコビアンの絶対値は、元の微小領域と新しい微小領域との面積の比率を表します。そのため、ヤコビアンは元の積分に関する情報を新しい変数での積分に適切に変換する役割を果たします。

この説明は線形性とは直接関係ありませんが、非線形変換（つまり、変換が座標に依存する場合）では、変換の「局所的」な性質を考える必要があるため、ヤコビアンが特に重要になります。それは新しい座標系の各点で微小領域が異なる方法で「変形」する可能性があるからです。

なお、ヤコビアンは変数変換の行列の行列式であり、元の座標系と新しい座標系との間の関係を局所的に直線的に近似することで計算されます。この直線的近似が、非線形変換における「微小」変化を適切に扱うために必要となるわけです。

ヤコビアン行列式は変数変換を行う際の多重積分を評価するために使用されます。これは、新しい座標系の微小ボリューム要素（平行六面体）の体積を計算するために必要です。

まず、n次元空間を考えます。この空間では、微小体積要素は通常、n個の直交ベクトルによって張られる直方体（または超立方体）として表現されます。例えば、3次元空間では、この直方体はdx、dy、dzの3つの辺を持ちます。

しかし、もし新しい座標系に変換すると（例えば、極座標や円筒座標など）、この微小体積要素は一般に平行六面体（または、そのn次元版）に変形します。この平行六面体の辺は、新しい座標系における微小変化に対応するベクトルによって定義されます。

n次元空間における平行六面体の体積は、その辺を形成するベクトルを行列として並べ、その行列式（determinant）を取ることで計算できます。これは、行列式が平行四辺形（2次元）、平行六面体（3次元）、その一般化（n次元）の体積を計算するための数学的な手段であるからです。

したがって、変数変換が行われた際の積分を正確に評価するためには、元の微小体積要素（直方体）から新しい微小体積要素（平行六面体）への変化を考慮する必要があります。このためにヤコビアン行列式が積分内で乗算の因子として現れます。ヤコビアン行列式は、変数変換によって生じた新しい座標系の微小体積要素の体積を正確に計算するための補正因子として機能します。

例：二次元正規分布

2つの確率変数が正の相関を持つ二次元正規分布に対して極座標変換を行い、その結果を確認します。二次元正規分布を生起し、極座標変換します。これにより、新しい確率変数RとΘが得られます。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal, norm
from scipy.integrate import quad
from scipy.integrate import nquad

# 平均と共分散行列
mu = np.array([0, 0])
cov = np.array([[1, 0.8], [0.8, 1]])

# 2次元正規分布を定義
rv = multivariate_normal(mu, cov)

# 極座標変換
def transformation(x, y):
    r = np.sqrt(x**2 + y**2)
    theta = np.arctan2(y, x)
    return r, theta

# 逆変換
def inverse_transformation(r, theta):
    x = r * np.cos(theta)
    y = r * np.sin(theta)
    return x, y

# ヤコビアン
def jacobian(r):
    return r

# 確率密度関数
def pdf(r, theta):
    x, y = inverse_transformation(r, theta)
    return rv.pdf([x, y]) * jacobian(r)

def pdf_without_J(r, theta):
    x, y = inverse_transformation(r, theta)
    return rv.pdf([x, y])

この場合のヤコビアンはｒです。

nquad関数は、複数の変数に対する積分を計算するためのもので、数値積分法（特にガウス・クワドラチャー法）を使用します。戻り値は２つで、最初の値は計算された積分値、二番目の値は計算された積分値の推定誤差です。この場合に積分する対象はpdfで与える引数はｒとθです。inverse_transformation(r, theta)でｘとｙに変換します。

# 積分
result, error = nquad(pdf, [[0, np.inf], [-np.pi, np.pi]])

print(f'Total probability: {result}')  # 結果はほぼ1になるはずです

result1, error = nquad(pdf_without_J, [[0, np.inf], [-np.pi, np.pi]])

print(f'Total probability without J: {result1}') 

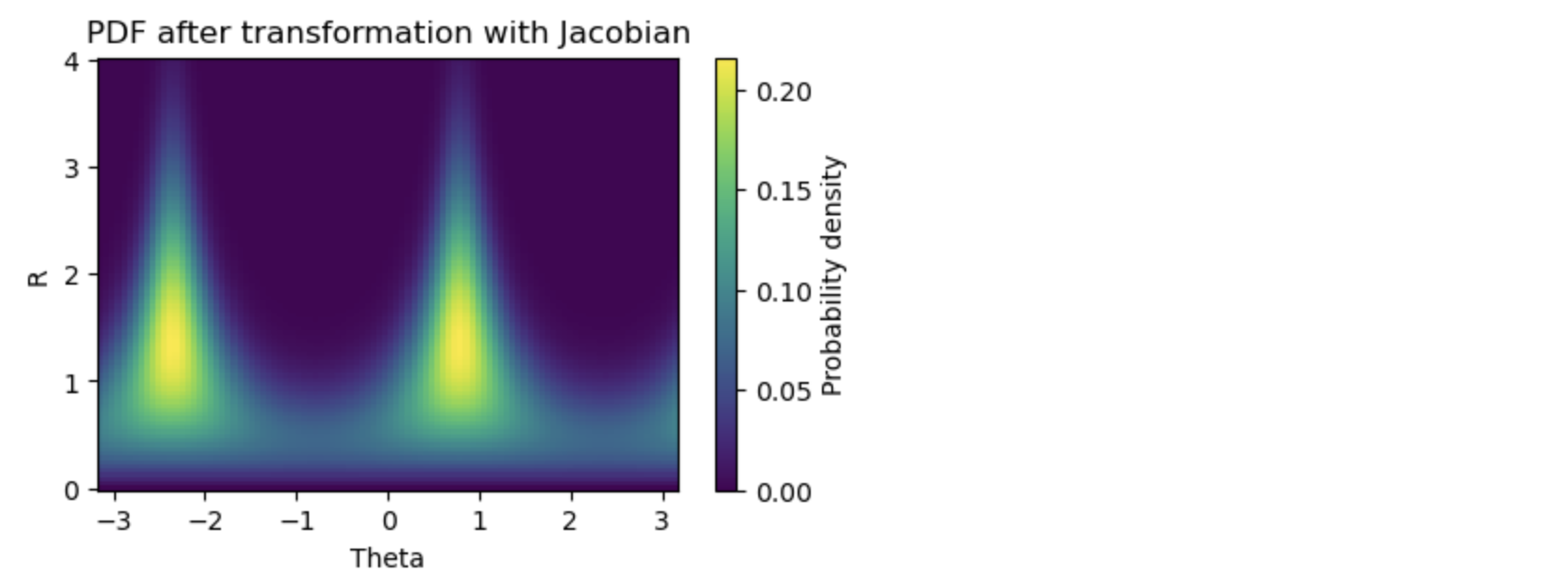
ヤコビアンのありなしで確率密度の大きさに明らなか違いが見えました。

次のコードは２重ループを使って、データ点の１つ１つをたどっていくので、ヤコビアンのやっていることが実感できるのではないかと思います。

# RとΘの値をサンプリング
r_values = np.linspace(0, 4, 100)
theta_values = np.linspace(-np.pi, np.pi, 100)

# 確率密度関数を評価
pdf_values = np.zeros((len(r_values), len(theta_values)))
for i in range(len(r_values)):
    for j in range(len(theta_values)):
        pdf_values[i, j] = pdf(r_values[i], theta_values[j])

# ヒストグラムを作成
plt.figure(figsize=(5, 3))
plt.pcolormesh(theta_values, r_values, pdf_values)
plt.colorbar(label='Probability density')
plt.xlabel('Theta')
plt.ylabel('R')
plt.title('PDF after transformation with Jacobian')
plt.show()

# RとΘの値をサンプリング
r_values = np.linspace(0, 4, 100)
theta_values = np.linspace(-np.pi, np.pi, 100)

# 確率密度関数を評価
pdf_values = np.zeros((len(r_values), len(theta_values)))
for i in range(len(r_values)):
    for j in range(len(theta_values)):
        pdf_values[i, j] = pdf_without_J(r_values[i], theta_values[j])

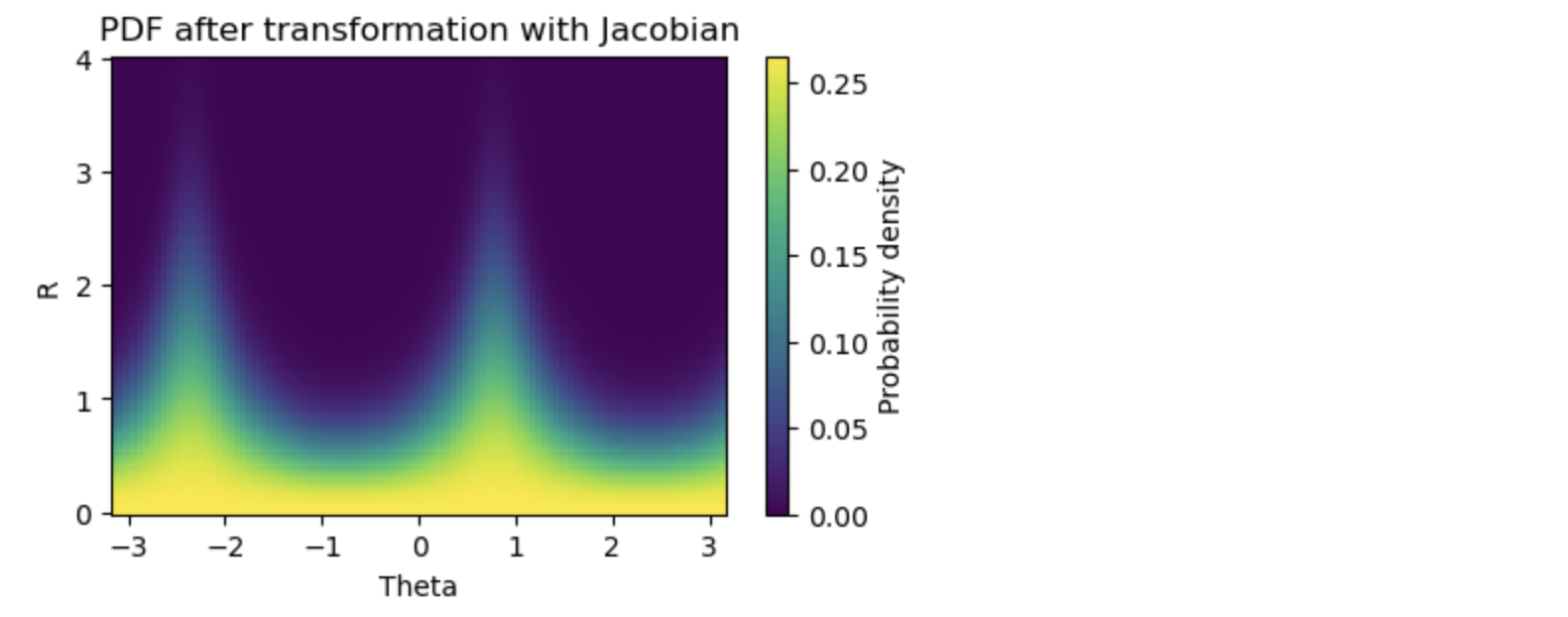
# ヒストグラムを作成
plt.figure(figsize=(5, 3))
plt.pcolormesh(theta_values, r_values, pdf_values)
plt.colorbar(label='Probability density')
plt.xlabel('Theta')
plt.ylabel('R')
plt.title('PDF after transformation with Jacobian')
plt.show()

例2: Z=aX+bY,W=Yという変換を考え、（Z,W）の分布を考える。このときのヤコビアンを計算し、Zの密度関数を求める。XとYは正規分布にしたがい、独立としてよい。また結果を乱数の生成を行い、その頻度図と比べて確認せよ。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, multivariate_normal

# Constants
a = 1
b = 2

# Create X and Y
mean = [0, 0]
cov = [[1, 0], [0, 1]]  # X and Y are independent
X, Y = np.random.multivariate_normal(mean, cov, 10000).T

# Transform to Z and W
Z = a * X + b * Y
W = Y

# The joint density function
rv = multivariate_normal(mean, cov)

# The grid
x = np.linspace(-10, 10, 500)
y = np.linspace(-10, 10, 500)
X_grid, Y_grid = np.meshgrid(x, y)

# Apply transformation and compute PDF
Z_grid = a * X_grid + b * Y_grid
W_grid = Y_grid
joint_pdf = rv.pdf(np.dstack((X_grid, Y_grid)))
jacobian = np.abs(a)  # Jacobian determinant
pdf_z = joint_pdf * jacobian  # Apply Jacobian

# Compute the mean and standard deviation for Z
mean_z = a * mean[0] + b * mean[1]
std_z = np.sqrt((a ** 2) * cov[0][0] + (b ** 2) * cov[1][1])

# Compare the pdf of Z with histogram of samples
plt.figure(figsize=(12, 6))

plt.subplot(1, 2, 1)
plt.hist(Z, bins=50, density=True, alpha=0.5, color='blue', label='histogram of Z')
plt.plot(x, norm.pdf(x, loc=mean_z, scale=std_z), 'r-', label='theoretical pdf of Z')
plt.title('Histogram of Z and theoretical pdf')
plt.legend()

plt.subplot(1, 2, 2)
plt.contourf(Z_grid, pdf_z, levels=100, cmap='jet')
plt.colorbar()
plt.title('PDF of Z and W')
plt.xlabel('Z')
plt.ylabel('Probability Density')

plt.tight_layout()
plt.show()