この記事は、先日の iOSDC Japan 2018 で発表した 「圏論とSwiftへの応用」 のスライドメモです。
来月10月16日に開催される プログラマのための圏論勉強会 - connpass の予習用の入門資料としてお使いください。
(さらに勉強したい方は、 圏論のオススメ勉強法(プログラマ向け) を合わせて読むと、キャッチアップしやすいと思います)
スライド・動画・補足記事
- Slide: 圏論とSwiftへの応用 / iOSDC Japan 2018 - Speaker Deck
- 動画: https://www.youtube.com/watch?v=zvrgfsDfxf8
- 関連記事:
スライドメモ

それでは発表を始めます。
本日のテーマは 「圏論」 です。
英語では、 Category Theory といいます。

圏論を「1枚の絵」で表すとしたら、このような図になります。
丸を書いて、矢印を書く。 たったこれだけ。簡単そうでしょう?

圏論を言葉で説明するとこうなります。
まず 「点」と「矢印」を使った学問 であること。
それは、 数学におけるFoundation.framework のようなものだと思ってください。
Foundationがないと、他のフレームワークが動かないですよね?それくらい重要な分野です。
その裏付けとして、圏論の 応用範囲は非常に広い です。
例えば、数学や論理学、計算機科学(プログラミング含む)、理論物理学など、ありとあらゆる科学分野で使われています。
また、圏論の素晴らしい点として、 数学の知識が無くても学べます。
そして圏論は、 関数型プログラミング において大活躍します。
今日はそれを見ていきます。

ちなみに、圏論の話は、 型システム にも密接に関係してきます。
例えば、再帰的な代数的データ型 や 全称量化(ジェネリクス)、 存在量化(Swiftプロトコル、existential container) といった、Swiftでおなじみの言語機能は圏論からも学べますし、さらには多相関数を引数として使える 高ランク多相、型コンストラクタを型引数として使える 高カインド多相、 値に依存する型が作れる 依存型 といった、より高度な「型レベルプログラミング」の概念にまで発展していきます。

つまり、 圏論を学ぶことで 「型」をより深く理解する ことができ、 現状のSwiftの理解 に加えて、 将来の可能性も見いだせる ということになります。
iOSエンジニアの私たちはこれまで、「C言語」「Objective-C」「Swift」と学んできたわけですが、 究極のゴールはずばり「圏論」 です。
ぜひ、今日の発表の通して、皆さんの中にある「究極生命体」が誕生してもらえればと思います。

ここで1つお断りとして、現在のSwift 4.2の言語仕様で圏論を語るには、どうしても足りない機能があります。
なので今日は、 「疑似Swift」 を使って説明します。
所々、シンタックスが変わっている点がありますが、その辺は、目を瞑ってもらえれば幸いです。

というわけで、まず最初に、 圏の定義 から見ていきましょう。

まず、先ほどの図式の丸を「点」と見なして、A、B、Cとラベル付けします。
これらの点のことを 「対象 (object)」 と呼びます。

それから、対象の間を「矢印」が張り巡っていきます。
これらの矢印のことを 「射 (arrow, morphism)」 と呼びます。
これら 対象と射をグルーピング したものを 圏 といいます。

圏の例としては、 プログラミングにおける「型」 があります。
点として「型」 を当てはめると、実は 矢印は「関数」 に相当します。
「型」と「関数」で構成される圏のことを 「型の圏」 といいます。

試しに、 String / Int / Bool を当てはめて、それらの間の関数を考えてみましょう。
思いつく限り、いろいろなパターンがあると思います。
そうすると、このような図を書くことができます。
なんとなく、圏のイメージが湧いたでしょうか?
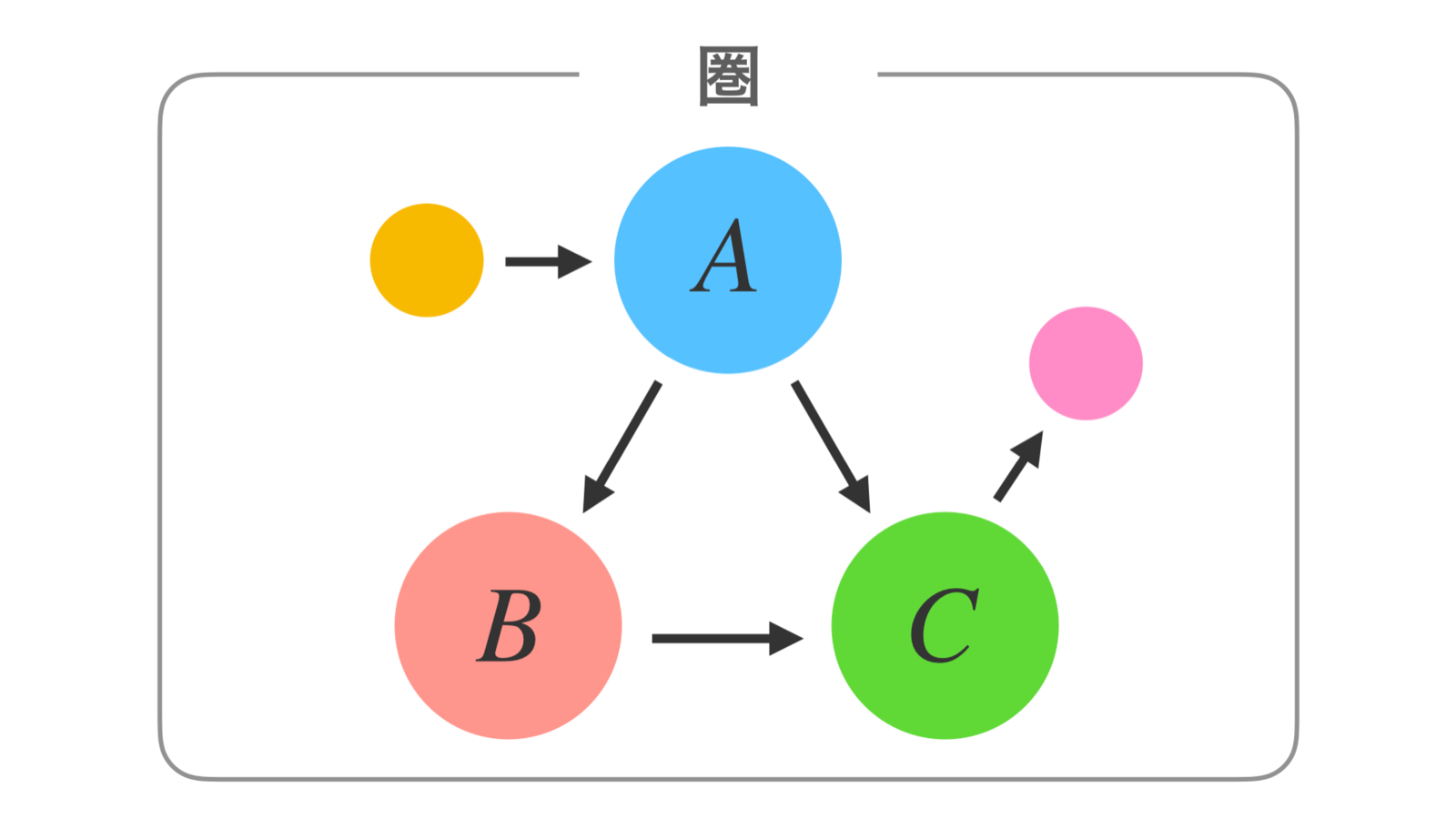
それでは前に戻って、 「圏」が満たすべき性質(定義) について簡単に紹介します。

まず、すべての点について、「恒等射」 とよばれる、自分自身へと向かう矢印が存在します。
この関数は、「呼び出したところで何もしない」関数になります。

次に、矢印は、A → B → C と連続で続く場合に、 「合成」 することができます。
この図の場合、f、gと続いたら、AからCは g ⚬ f という矢印を作ることができます。
ここで、 ⚬ は 合成演算子 です。

例えば、型の圏で、2つの関数 count と isEven があったとしたら、それらを合成して、 isEven ⚬ count と1つの関数にまとめることができます。
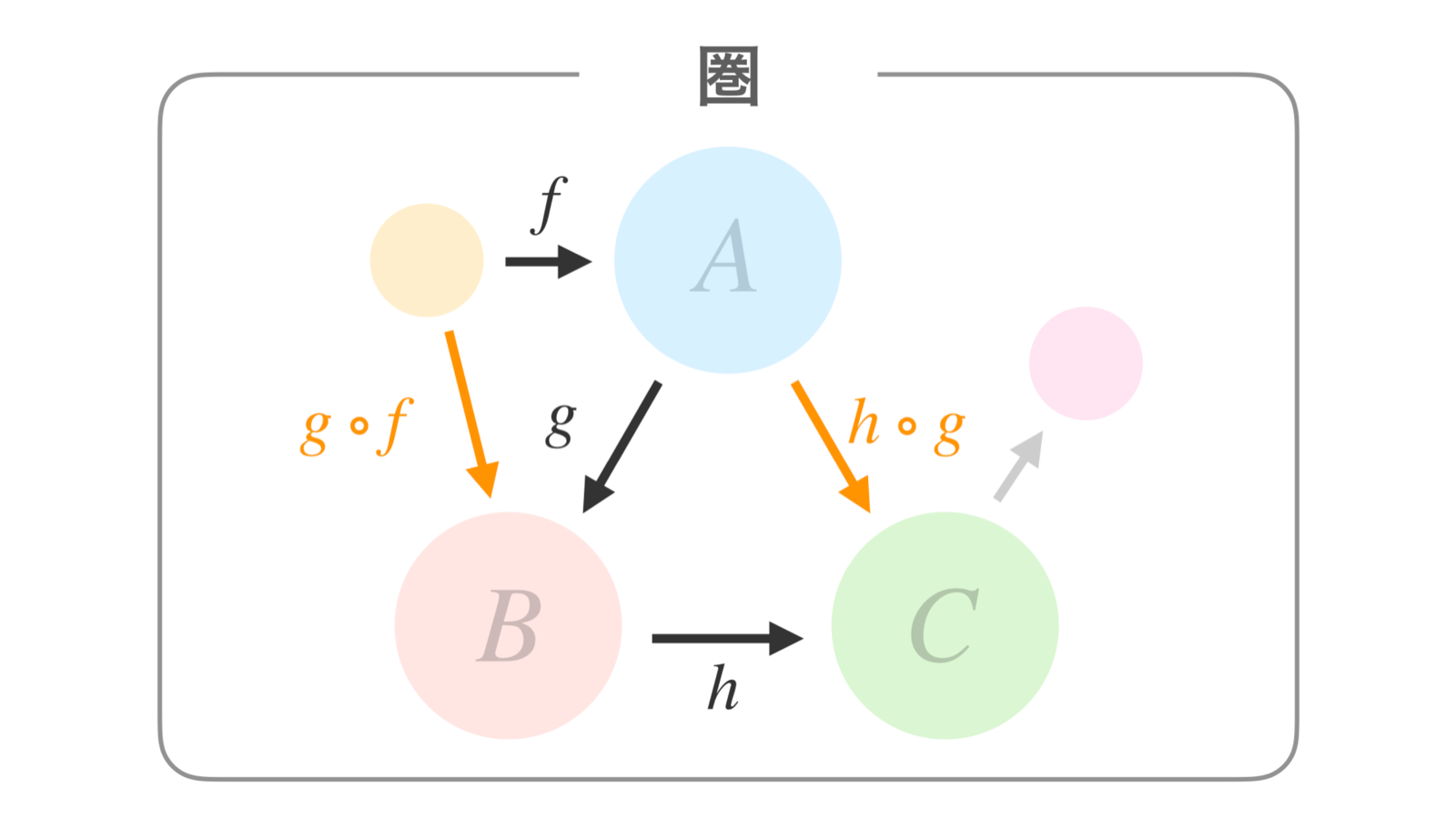
ここで、合成に関する重要な規則があります。
例えば、黒の矢印 f、g、h の3つがあった場合、まず2つを合成したオレンジの矢印ができて・・・

それから「オレンジと残りの黒い矢印を合成」すると、「赤の矢印」ができます。
これは、 右回りと左回りの2パターンの作り方があって、それらは共に等しいです。
つまり、 f、g、h の合成の順序はどちらから先にやっても良い ということです。
これを 「結合律」 と呼びます。

以上をまとめると、圏の定義はこのようになります。
他にも、 「domain / codomain」 という用語があり、矢印の「開始地点」と「終了地点」という意味です。

これをSwiftで表現すると、こうなります。
- まず、恒等射に関しては、
func idというものが作れます。
これは、 ジェネリックなAを渡したらAがそのまま返ってくる、何も計算しない関数 です。 - もうひとつ、合成に関しては、
func ⚬という記号をここでは使います。 2つの連続する関数を受け取ったら、内部でそれらを順番に呼ぶ関数 です。
圏の定義については、まずはこの2つの関数を覚えておけば合格です。

次に 「関手」 を見ていきましょう。
英語では 「Functor」 といいます。

「関手」を大雑把に説明すると、 「左の圏」を丸ごと対象として、中身の形をそのまま維持しながら「右の圏」へと写す「射」 になります。(上の図のオレンジの矢印のことです)

つまり、内部の対象がそのままの形で写り・・・

さらに、射がそのままの形で写ることで、 内部の形(構造)がそのまま維持 されています。
これが「関手」の定義です。

例えば、型の圏で考えるなら、 「配列 Array」は関手の1つ です。
左側のプリミティブな型に対し、その配列を作ると、右側の関数は、map を使って写すことができます。

ちなみに、圏論での一般的な表現は、このようになります。
先ほど Array や map と書いていたところが、F に置き換わっています 。
ここで注目してほしいのは、右側の黒い矢印の F(g ⚬ f) です。

実は、右側の圏だけに着目すると F(f) と F(g) という矢印がすでに存在しています。
つまり、これらを合成すると、 F(g) ⚬ F(f) となって、やはり黒の矢印が得られます。

関手の定義は、 F(g ⚬ f) と F(g) ⚬ F(f)を等しいものとして扱います 。

というわけで、関手についておさらいすると、こうなります。
関手は基本的に、 圏から圏へのマッピングで、形を保つもの と覚えてください。

では試しに、関手をSwiftで書くと、どうなるでしょう?
残念ながら、現在のSwiftは、言語仕様上、関手を作ることはできません。
が、今は疑似Swiftの世界なので、何でもありです。
なので、試しにこんなprotocolを書いてみました。
注目してほしいのは、 static func map です。
これはスタティックメソッドですが、 第一引数に self をおくことで、インスタンスメソッドとしても使えるというルール にします。
そうすると、Array を Functor に適合させれば、配列の map は、下の使用例のコードのように「中身を入れ替える」操作になります。

この例から言えることは、2つ:
- まず、 関手とは「
mapができる」こと - そして
mapとは、「コンテナを変えずに中身を変える」 こと
ちなみに、これはこれで正しいのですが、いわゆる pointwiseな考え方 です。
実はもっと素晴らしい、関数型的な見方があるので、紹介したいと思います。

先ほど、static func map の第一引数に self をおく話をしました。
が、今度は下のprotocolのように、 self を第二引数においてみます。
これは、引数順序を入れ替えただけなので、同じ結果になります。
そして、これをさらにカリー化します。
すると、別の形の static func map が得られますが、型から分かるように、 「map は A -> B の関数から F<A> -> F<B> の関数への変換」 を表しています。
これを 関数持ち上げ (リフト、lifting) と言います。

これを図式で説明すると、まさに先ほどの通りです。
ああ、単に f が F(f) に写っただけ だね、と。たった、それだけのことです。
が、 とても重要なものの見方 なので、ぜひ覚えていって下さい。

この考え方は、登場人物が関数(つまり射)しか存在しないので、「射が中心の、 pointfree な考え方」 といいます。
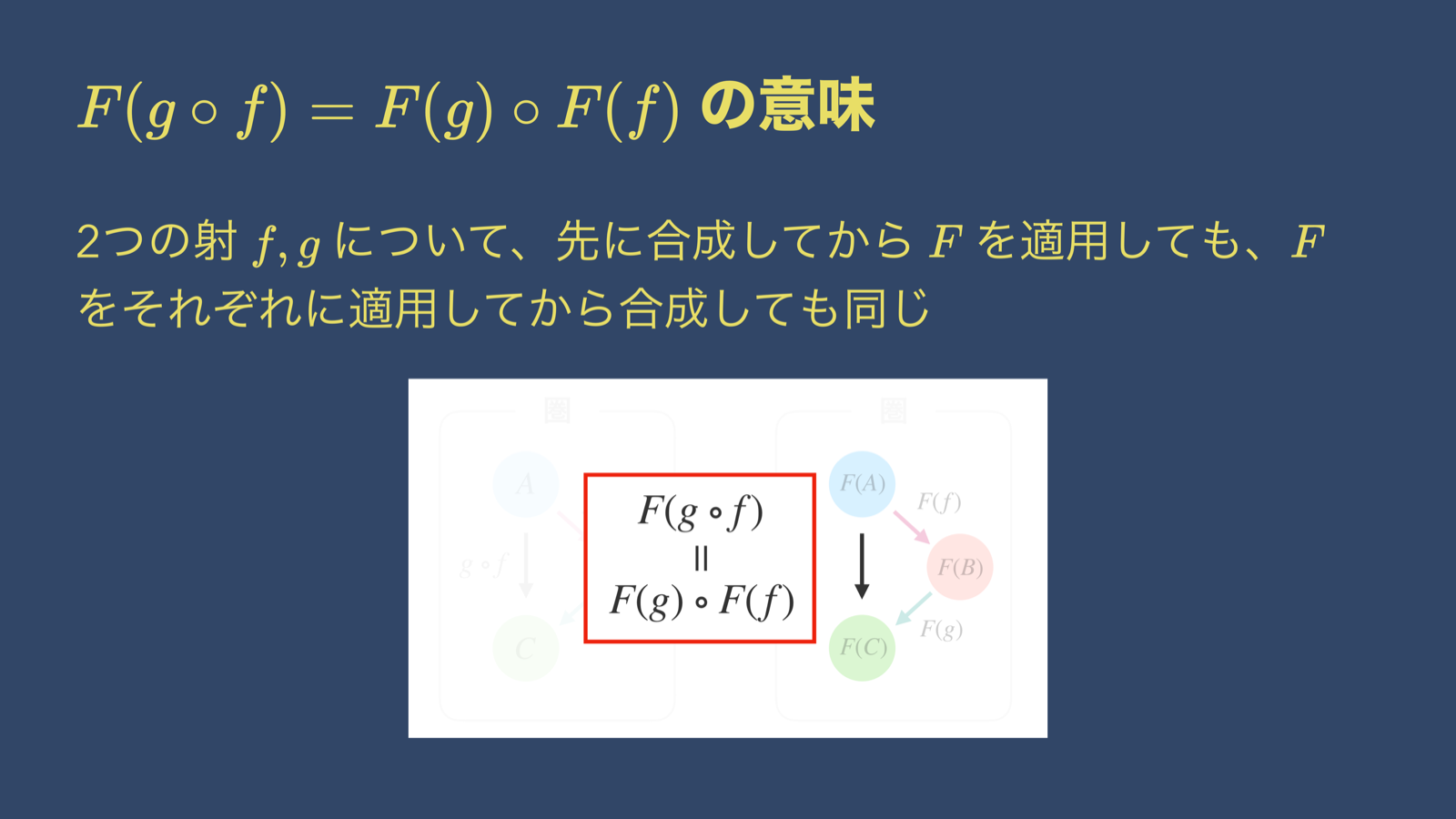
さて話を戻して、先ほど F(g ⚬ f) は F(g) ⚬ F(f) に等しい、という話をしましたが・・・

これをSwiftで説明すると、こうなります。
すなわち、 関数合成してから map を1回行う のと、 個々に map を呼んでから関数合成する ことは同じです。
ちなみに、 「 map を2回行う」ということは、2回 for文を回しているようなもので、中間表現を作ることなので、無駄なコストが発生 しています。
なので、mapを1回にするだけの方が、パフォーマンス改善につながりますし、こういうのは 最適化できる余地 があります。
なので、 コンパイラ方面に興味のある人 にとっても、圏論は非常に有意義な学問なんですね。

ここで余談として、今まで2つの圏を区別して考えてきましたが、
実際のところはどちらもSwiftの型なので、 1つの圏としてまとめて扱うことができます 。

そうすると、このような図になります。
関手 Array は自分自身の圏に向かう射になります。これを 「自己関手」 と呼びます。
実は、 私たちが普段 Functor と呼んでいたものは、自己関手 (Endofunctor) のこと だったんですね。

では続きまして、 「自然変換」 について説明します。
英語で、Natural Transformationといいます。

「自然変換」は、先ほど話した関手が 同じ方向に2つあるパターン です。
関手FとGがあって、それぞれ左の圏の構造を右に反映している のが分かります (黄色と緑の点線)。

ここで、自然変換の定義は、 本来矢印である2つの関手を対象とみなして、「その間にさらに伸びる射」 になります。
これはつまり、 関手の間にさらに関係性がある(矢印の間にさらに矢印がある) ことを意味します。
この自然変換αは、写った先の圏では、「複数のジェネリックな射」として現れます。
そう、実は 自然変換とはジェネリック関数 のことなんですね。
別名、多相関数 とも言います。

ここで注目してほしいのは、 関手によってできた黒の矢印 と、 自然変換によってできた赤の矢印 が組み合わさって、四角形ができていることです。
実はこの四角形は、右回りの合成でも、左回りの合成でも、どちらも等しくなります。
これを 可換図式 といいます。
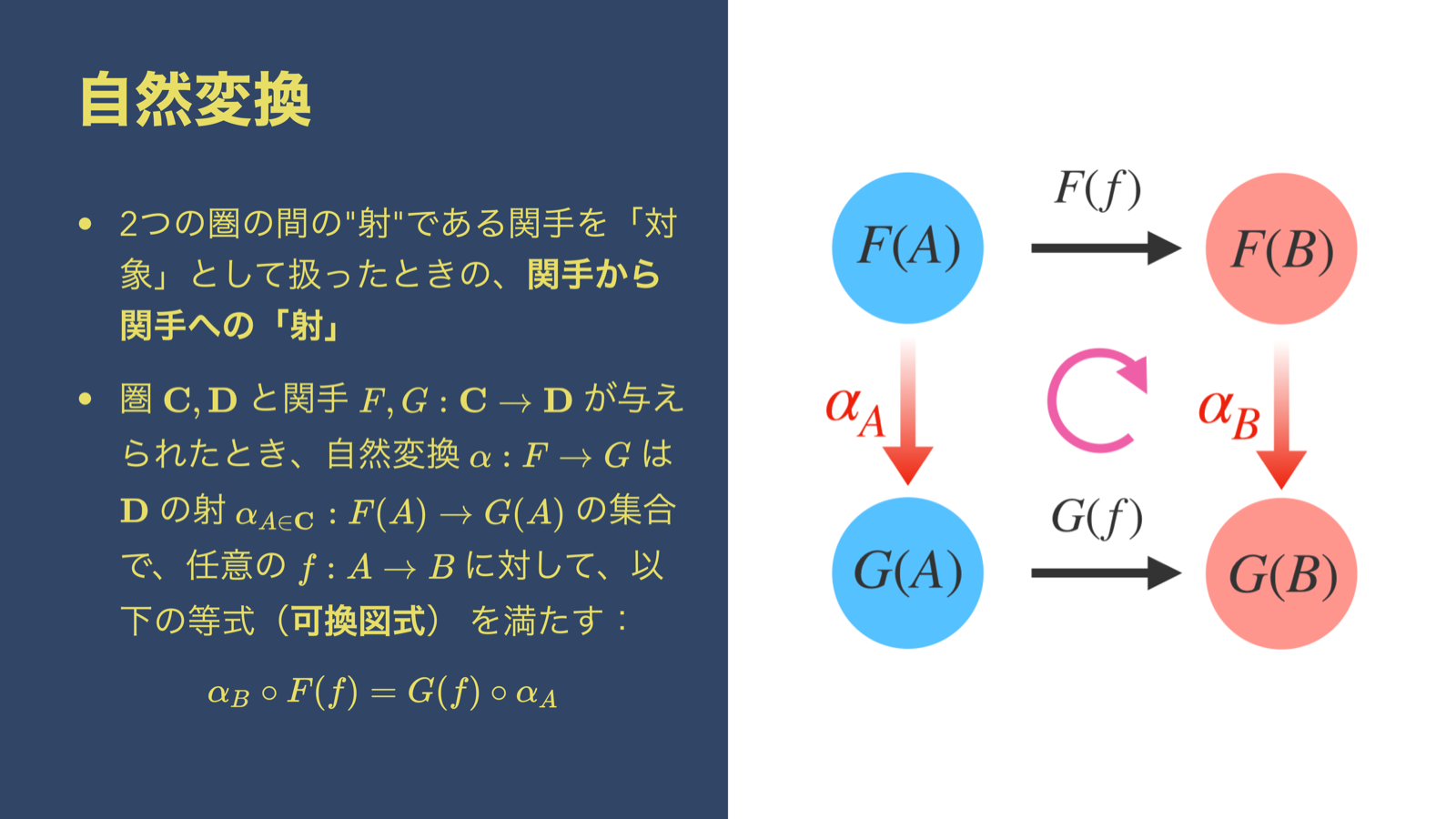
というわけで、今述べた自然変換の定義がこちらです。

この意味をSwiftで説明すると、こうなります。
まず 自然変換の関数の型は F<A> -> G<A> で、中身を変えずにコンテナを変える「ジェネリック関数」 を表します。
そして、これを func alpha とおくと、実は、 先にmap してから自然変換 alpha を計算しても、先に自然変換 alpha してから map しても同じ であることが言えます。

試しに、配列の最初の要素を取ってくる Array.first を例にとってみましょう。
これは Array から Optional へのジェネリック関数 なので、まさに自然変換の形です (NOTE: Optional も関手の1つ)。
そして、先ほどの可換式に当てはめると、このように書けます。
つまり、 map で文字列変換してから「最初の要素を取り出し」 ても、 「最初の要素を取り出し」てから map で文字列変換しても結果が変わらない ということです。
普段、プログラミングしていたら当たり前のように見える話ですが、これをきちんと形式化したものが自然変換になります。
ここで重要なのは、 どちらのフローで計算しても結果が変わらないのだとしたら、 計算量が少ない方が良い に決まっていますよね?
この場合ですと、「最初の要素を取り出し」てから map した方が早いので、ここでも コンパイラの最適化の余地がある といえます。

続いて 「米田の補題」 です。
英語では Yoneda Lemma といいます。

「米田の補題」は、先ほどの自然変換の話において、 「Hom関手」と呼ばれる「関数の集合の関手」 というものを考えることで、導くことができます。
ただ、それを説明するために30分の発表では短すぎるので、雰囲気だけお伝えします。
参考: iOSDC Japan 2018 で発表した「圏論とSwiftへの応用」の補足 - 米田の補題について - Qiita

まず、右の「集合の圏」にあるこの青い集合。
通常は、空っぽの集合(値が入っていない)の場合もありうるのですが、「Hom関手」を使う場合は特別で、この場合だと $\mathrm{id}_A$ という恒等射が値が必ず存在します 。

すると、右上の赤い集合には $f$ が必ずいて・・・

そして 自然変換α を通して、下の集合にも値が入ってきます。
つまり、 すべての集合に、値が必ず存在します。

これの意味は、まず 自然変換 $\alpha$ が決まれば、必然的に $\alpha_A$ の値が求まります し・・・

逆に $\alpha_A$ が決まると、可換図式から、$\alpha_B$、$\alpha_C$ ...も決まって、結果的に自然変換 $\alpha$ そのものが決まります。

これを 米田の補題 と言い、式で表すとこのように書けます。
上の式はHom関手の意味を知らないと分かりにくいですが、型で表現した下の式は、もう少し簡単になります。
これの意味するところは、 左辺の「自然変換(つまりジェネリック関数)」の型 と、 右辺の「値」の型 が1:1の関係になる、ということです。
関数と値が同じになる ・・・なんだか、すごくないですか?

実際に、Swiftで例をお見せします。
例えば、let fa という「値」と、それを「ジェネリック関数」で包んだ func closure、つまりクロージャーがあったとしたら、 両者は同じものとみなせます 。
これはつまり、 「同型」の関係 です。
「同型」の意味は、お互いに 相互変換が可能 ということです。

実際に、相互変換するコードをSwiftで書くと、このようになります
上の関数 faToClosure は、「値から自然変換」に変換。
下の関数 closureToFa は、「自然変換から値」に逆変換します。
実装方法に関しては、この書き方以外にありません。
ちなみに下の closureToFa は、引数にジェネリック関数を受け取っていますが、これは ランク2多相 と呼ばれるもので、残念ながらまだSwiftには実装されていません。

一応、参考までに、 「同型」の話 についてもっと知りたい方は、以前、私が発表した「代数的データ型」の資料がありますので、機会があったらぜひチェックしてみてください。
参考: Algebraic Data Type in Swift - Speaker Deck

では、この米田の補題から、どういったことが分かるでしょうか?
一つの例として、**「CPS変換」**があります。
CPSというのは Continuation Passing Style の略で、 「継続」と呼ばれるコールバック形式の書き方 だと思ってください。
米田の補題では、 F(T) = T とおくと継続 が得られ、 F(T) = X -> T とおくと、米田埋め込み と言われる 「CPS変換」 が得られます。
後者は、 ∀B. (A -> B) -> (X -> B と X -> A が同型(相互変換が可能)なので、「右辺から左辺に変換する関数」として、実際にSwiftのコードで書いてみると、下のような func cpsTransform が書けます。

それでは、この「CPS変換」は一体何の役に立つのでしょうか?
実は、 「末尾再帰の最適化」 の話に関係してきます。
例えば、上のコードのように、階乗を計算する func factorialがあったとします。
これは末尾再帰の形ではないので、nの数が大きくなるほど、スタックを食いつぶして、最終的にオーバーフローでクラッシュします。
ここで、先ほどの CPS変換 cpsTransform を使うと、あら不思議、 継続を使った、末尾再帰のコードに勝手に最適化 されました。
ちなみにSwiftコンパイラは、裏側でこのような末尾再帰最適化を自動で行っているので、普段のiOS開発で意識することはほとんどないでしょう。

・・・というわけで、米田の補題はここまで。
それでは本日のメインディッシュである 「随伴」 を見ていきます。
英語で Adjunctionといいます。
随伴は、圏論だけでなく、Swiftプログラミングにおいてもとても重要な概念です。

図で説明すると、このようになります。
まず2つの圏があり、関手F とG がそれぞれ 逆方向 に伸びています。
そして、何か C と D という対象があったら、F(C)、U(D) に写したりできます。

ここで、青と赤の対象の間の ピンク色の「矢印の集合」 に注目すると・・・

随伴の定義は、 「射の集合」が「1:1の関係」 になることです。
つまり、2つの圏が同型(や同値)ではなく、それを弱めた「射の集合のみが同型」 になります。
同型であることは、つまり 「左側の射の集合」から「右側の射の集合」に変換する関数 leftAdjunct と、逆変換 rightAdjunct の2つの関数を定義する ことができます。

随伴の関係を式で書くと、このようになります。
ちなみに ⊣ は随伴の記号 です。
F、Uをそれぞれ、 左随伴関手、右随伴関手 と呼びます。

随伴の(直接的・間接的な)関係は、実に様々なパターンがあります。
例えば、
- 足し算と掛け算が、対角関手を経て、間接的につながっている
- (この後話す) タプル(積)と関数(指数対象)
- 存在量化(プロトコル)と全称量化(ジェネリクス) の間接的な関係
- 自由関手と忘却関手
などがあります。

それでは、随伴を疑似Swiftを使って表してみましょう。
随伴を定義するには、leftAdjunct と rightAdjunct が必要 でした。
なので、このようなprotocolの形で書けると思います。

試しに、左随伴にタプル、右随伴に関数型を使うSwiftの例を上げます。
typealias で Tuple<A, B> と Func<A, B> を用意します。

まず、関手であることを示すために、protocol Functor を採用します。
すると、このような形で書くことができます。

それから protocol Adjunction を採用すると、このようになります。
ここで注目してほしいのは、 leftAdjunct と rightAdjunct の中身 です。
-
leftAdjunctは、cを引数に、aを引数にそれぞれ受け取り、タプルにしてから関数fに適用している -
rightAdjunctは、タプルを引数に受け取ってから、個々に分解して、関数fにそれらを部分適用 している
つまり、 個々の引数をタプルにまとめたり、逆にタプルを個々の引数に分解している わけです。
・・・これらのメソッド、何かに見覚えがありませんか?

そう、 カリー化 ですね。
見覚えがあるかもしれませんが、 func curry と func uncurry はこのように書けます。
参考: https://github.com/thoughtbot/Curry

というわけで、タプルと関数型の随伴の場合、 leftAdjunct と rightAdjunct は、実は func curry と func uncurry に対応します。

次に、随伴のもう一つの定義を見ていきます。

先ほど、2つの圏の射 $f$ と $\overline{f}$ は、1:1 で対応している、という話をしました。

ここで、2つの関手 F と G を 1回ずつ適用して戻ってくる場合 を考えてみます。
すると、このような図が書けます。
(前の状態に戻ってきていないので、随伴が同型とは異なることが分かります)
ここで、新しくできた F(U(D)) と U(F(C)) について、それぞれどのような関係があるかを見てみます。

まず、関手の性質で、これら黒の矢印は、関手 F、 G によるリフトであることが分かります。

次に、随伴関係から、実は ピンクの射の集合もまた1:1の関係 があります。
(3つ前のスライドで、 D = F(C) とおくことで、左の圏の2つの対象が1つにつぶれるイメージです)
ここで、 左の対象には必ず1つ以上の射があり、それが id です。
それを leftAdjunct して対応する右側の圏の射を unit (単元) と定義します。

同様に、右の圏のid に対応する左の圏の射を counit (余単元) と定義します。

そうすると、この図のような三角形が出来上がるわけですが、これらは可換になります。

いま見てきたことは、 leftAdjunct/rightAdjunctの代わりに、 unit/counit を使っても随伴が定義できる 、というものです。

さて、ここでちょっとした型遊びをします。
先ほどの counit: F<U<D>> -> D で、 D はどんな型でも良いので、 試しに D = F<C>を代入してみます。
すると、 counit: F<U<F<C>>> -> F<C> になります。
これをさらに 関手 U でリフトすると、 U<F<U<F<C>>>> -> U<F<C>> が得られます。
これを join という名前の関数 で定義します。

すると、このようにまとめられますが、ここで、U<F<...>> というのがたくさん出てきているので、U<F<C>> = M<C> とおいてしまいます。

すると、このようにシンプルになりました。
こうなると、さらに join と map を組み合わせて flatMap なんてのも作れたりします。
・・・ん? flatMap?
どこかで聞き覚えがありますね。

そう、実はこのM、 モナド のことなんです。

モナドは、簡単に言うと、 右随伴関手に左随伴関手を合成したもの です。
そして、 合成したものは、元の圏に戻ってくるので、モナドは自己関手 です。
これによって、 「モナドは自己関手の圏における◯△□・・・」 というところまで言えるようになりました。

さて、このモナドですが、先ほどのタプルと関数型の例を使って、実際に作ってみましょう。
右随伴関手(関数)に左随伴関手(タプル)を合成するということは、 「関数の中にタプルを入れる」 ことになるので、型としては S -> (A, S)。
実はこれ、 状態モナド のことです。
関数型プログラミングを知っている方なら、 状態モナドが圏論と密接に絡んでくる と知って、胸が熱くなるポイントではないかと思います。

ですが、私たちが知りたいのは、モナドよりもさらに先の世界です。
いや、むしろ 一周回って「逆の世界」 を考えてみましょう。
そう、モナド U(F(C)) の逆 F(U(D)) を考えてみます。

すると、先ほど モナドで出てきた関数の向きがすべて逆 になります。
unit だったものは counit に、 join は duplicate と呼ばれる関数に変わります。
そして、 モナドのMの文字もまた逆さになり、Wという記号 を使います。

そう、この「Mの双対」とも言われる、ライバル的存在・・・

これを 「Comonad」 といいます。
日本語では「余モナド」ともいいます。

コモナドもまた、随伴からF(U(D)) という形で作ることができます。

実際にSwiftの例に落とし込んでみます。
すると、モナドのときとは逆で、今度は 「タプルの中に関数を入れる」 形になります。
すると、このような struct Store 型が作れます。
これを 余状態余モナド といいます。

ただ、 余状態余モナド自体はあまり面白くないので、ここでさらに 余代数 (Coalgebra) を考えてみます。
余代数というのは、とりあえず S を追加で引数に取る ものだと思ってください。
すると、なんということでしょう、レンズ が出来上がりました。
レンズは、皆さんご存知でしょうか?
簡単にいうと、すごいgetter/setterみたいなものです。
参考: SwiftでLens(すごいgetter/setter)を実装してみた - Qiita

つまり、一言でいうと、こういうことです。
「レンズは余状態余モナドの余代数だよ。」
・・・すみません、これを言ってみたかっただけでした。

というわけで、まとめです。
今日の発表では、 圏の定義 から始まり、 関手 、 自然変換 、 米田の補題 、 随伴 を学んだと思ったら、いつの間にか モナドとコモナド が出てきて、 状態モナドやレンズ の話にまで発展しました。
後半は、関数型プログラミングを知っていないと、いまいちピンとこないと思うので、ひとまず関数型ポエムだと思って聞き流してください。
初めて圏論を学ぶ人は、「関手と自然変換」まで理解できれば十分 だと思います。

もし、もっと深く圏論を学んでみたいという方は、さらに面白いテーマが控えていますので、ぜひこちらもチェックしてみてください。

参考文献(初学者向け)
- Bartosz Milewski's Programming Cafe | Category Theory, Haskell, Concurrency, C++
- 📺 TheCatsters - YouTube
- Category theory for beginners
- 圏論勉強会 @ ワークスアプリケーションズ
- プログラマーのための圏論(上) - bitterharvest’s diary
参考: 発表後に、こちらの記事を書きました

参考文献(中〜上級者向け)
- 📚 圏論 原著第2版 | Steve Awodey
- 📚 ベーシック圏論 普遍性からの速習コース | Tom Leinster
- 📚 圏論の基礎 | Saunders MacLane
- 圏論 | 壱大整域
- 檜山正幸のキマイラ飼育記
- nLab

というわけで、今日の発表を終わりにしたいと思います。
ご清聴ありがとうございました。