p5.jsでマウスで描いた折れ線を滑らかにする

はじめに

　マウスで直前の位置を記録しながら点を取得して置き続けると折れ線ができる。これを滑らかにする。
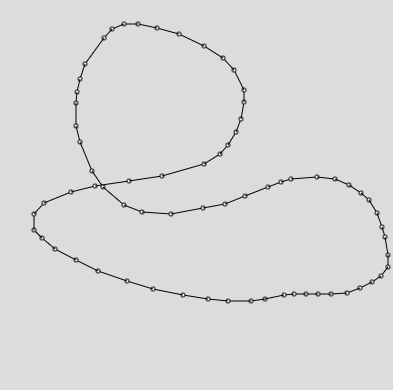
　マウスダウンで発火させて、直前の点との距離が10以上の時に新しい点を追加する。ここで制限を設けないと際限なく点が追加されてしまうからである。そうして点をつなぐと折れ線ができる。こんな感じで。

　これをなるべく滑らかにしたい。こんな感じで。

　滑らかというのは曲線の向きがなるべく滑らかに変化し続けるという意味である。不自然にガタガタしないということ。それも主観によるが、ここではそういうものとして議論する。
　ざっくりとした方針としては、適当に若干幅を持って点をいくつか取り、それらをアンカーとして2次ベジエで近似し、近似してから点列に直し、そのあとでさらに均等割りをする。

コード全文

　point draw

let mypoints = [];
let isActive = false;
let isClosed = false;

function setup() {
  createCanvas(400, 400);
}

function draw() {
  background(220);
  if(mouseIsPressed && mypoints.length>0 && isActive){
    const p = mypoints[mypoints.length-1];
    if(dist(p.x,p.y,mouseX,mouseY)>10){mypoints.push(createVector(mouseX,mouseY));}
  }
  for(let i=0; i<mypoints.length; i++){
    circle(mypoints[i].x,mypoints[i].y,4);
    if(i<mypoints.length-1){
      line(mypoints[i].x,mypoints[i].y,mypoints[i+1].x,mypoints[i+1].y);
    }
  }
  if(mypoints.length>0&&!isActive){
    if(isClosed){ line(mypoints[0].x,mypoints[0].y,mypoints[mypoints.length-1].x,mypoints[mypoints.length-1].y); }
  }
}

function mousePressed(){
  if(mypoints.length==0){
    mypoints.push(createVector(mouseX,mouseY));
    isActive=true;
  }
}

function mouseReleased(){
  if(!isActive) return;
  const closed = (mypoints[0].dist(mypoints[mypoints.length-1]) < 24 ? true : false);
  evenlySpacing(mypoints, {minLength:24,closed, showDetail:true});
  quadBezierize(mypoints, {detail:8, closed});
  evenlySpacing(mypoints, {minLength:12,closed, showDetail:true});
  isActive = false;
  isClosed = closed;
}

function evenlySpacing(points, options = {}){
  const {minLength = 1, closed = false, showDetail = false} = options;

  // closedの場合はおしりに頭を付ける
  // そして最後におしりを外す
  const q = points.slice();
  if(closed){ q.push(q[0].copy()); }

  // まず全長を計算する
  let totalLength = 0;
  for(let i=0; i<q.length-1; i++){ totalLength += q[i].dist(q[i+1]); }
  // 分割数
  const N = Math.floor(totalLength/minLength) + 1;
  // セグメント長
  const l = totalLength/N;

  // lを基準の長さとして分けていく。まず頭を採用する。次の点と差を取る。これの累積を
  // 取っていってlを超えるようならそこで比率を計算しlerpして加えて差分を新しい
  // elapsedとする。
  let elapsed = 0;
  const prev = q[0].copy();
  const next = createVector();
  const result = [q[0]];
  for(let i=1; i<q.length; i++){
    next.set(q[i]);
    const d = prev.dist(next);
    if(elapsed + d < l){
      elapsed += d;
      prev.set(next);
      continue;
    }
    // prevとnextをratio:(l-elapsed)/dで分割。

    // この時点でelapsedはlより小さいことが想定されている。が...
    // 厳密にやるならelapsed+d>=lであるからして
    // (l*m-elapsed)/dによるlerpをelapsed+d>=m*lであるすべてのmに対して実行し
    // elapsedにd-m*lを足して終わりにする. m*l <= elapsed+d < (m+1)*lなので
    // 0<=elapsed+d-m*l<lである。
    // 数学のお時間です。
    // mの想定される上限値というのはおおよそ(elapsed+d)/lですが、
    // elapsedはl以下が想定されているし、dはtotalLength以下。
    // そしてd/lというのはtotalLength/lで抑えられる。これは何か。Nである。つまり？
    // mがN+1より大きくなることは「ありえない」。安全のためN+2をとっても、
    // せいぜいそのくらい。だからm>N+2になったらbreakしていい。
    // 無限ループにはならない。その場合はもうelapsedを0にしよう。
    let m=1;
    while(elapsed + d >= m*l){
      const newPoint = p5.Vector.lerp(prev, next, (m*l - elapsed)/d);
      result.push(newPoint);
      m++;
      if(m > N+2) break;
    }
    elapsed += d-(m-1)*l;
    if(m > N+2) elapsed = 0;
    prev.set(next);
  }
  // 最後の点が入ったり入んなかったりするのがめんどくさい。
  // そこで
  // 最後の点についてはもう入れてしまって
  // 末尾とその一つ前がl/2より小さいときにカットする。
  result.push(q[q.length-1].copy());
  if(result[result.length-1].dist(result[result.length-2]) < l/2){
    result.pop();
  }
  // closedの場合は末尾をカットする
  if(closed){ result.pop(); }

  points.length = 0;
  points.push(...result);

  if(showDetail){
    let minL = Infinity;
    let maxL = -Infinity;
    for(let i=0; i<points.length; i++){
      if(!closed && i===points.length-1) break;
      const d = points[i].dist(points[(i+1)%points.length]);
      minL = Math.min(d, minL);
      maxL = Math.max(d, maxL);
    }
    console.log(`minL:${minL}, maxL:${maxL}`);
  }
}
// これで決定版でいいと思います。

// クワドベジエライズ
// 中点を取り、もともとの点を制御点とする
// openの場合は0のみ残し、0-1点と直線でつなぐ			
// そしてL'-LとLを直線でつなぐ
// closedの場合は0-1からスタートし、最後に0=Lを制御点とし、L'-Lと0-1をベジエでつなぐ
// 感じですね。
function quadBezierize(points, options = {}){
  const {detail = 4, closed = false} = options;
  const subPoints = [];
  for(let i=0; i<points.length-1; i++){
    subPoints.push(points[i].copy().lerp(points[i+1], 0.5));
  }
  if (closed) {
    subPoints.push(points[points.length-1].copy().lerp(points[0], 0.5));
  }
  const result = [];
  if (!closed) {
    result.push(points[0]);
    result.push(subPoints[0]);
    for(let k=1; k<subPoints.length; k++){
      const p = subPoints[k-1];
      const q = points[k];
      const r = subPoints[k];
      for(let m=1; m<=detail; m++){
        const t = m/detail;
        result.push(createVector(
          (1-t)*(1-t)*p.x + 2*t*(1-t)*q.x + t*t*r.x,
          (1-t)*(1-t)*p.y + 2*t*(1-t)*q.y + t*t*r.y,
          (1-t)*(1-t)*p.z + 2*t*(1-t)*q.z + t*t*r.z
        ));
      }
    }
    result.push(points[points.length-1]);
  } else {
    result.push(subPoints[0]);
    for(let k=1; k<=subPoints.length; k++){
      const p = subPoints[k-1];
      const q = points[k%subPoints.length];
      const r = subPoints[k%subPoints.length];
      for(let m=1; m<=detail; m++){
        const t = m/detail;
        if(m===detail&&k===subPoints.length)continue;
        result.push(createVector(
          (1-t)*(1-t)*p.x + 2*t*(1-t)*q.x + t*t*r.x,
          (1-t)*(1-t)*p.y + 2*t*(1-t)*q.y + t*t*r.y,
          (1-t)*(1-t)*p.z + 2*t*(1-t)*q.z + t*t*r.z
        ));
      }
    }
  }
  points.length = 0;
  points.push(...result);
}

インタラクション

　マウスダウンで点が用意される。以降、mouseIsPressedがtrueである限り、新しい位置が前の位置と10以上離れるたびに、新しい点が追加され、その点が新しい「前の位置」になる。これにより際限なく点が追加されていく挙動を回避できる。そのたびに点を円で、線を線で描画する。マウスを離すと描画が終わる。最後に追加した点までの折れ線が生成される。
　そして、これを加工する。加工することで滑らかになる。

evenlySpacing（均等割り）

　いわゆる均等割りである。

　まずこれは引数であるベクトル列（points）を改変する内容で、新しく点列を返すわけでは無いので注意。最後に新しく作った点列でまるごと置き換えている。

　方針としては、まず全長を取る。これは素直に全長を計算するだけ。小細工はしない。そのうえで、optionsであるminLengthで全長を割る。割って得られる整数部分に1を足して、これを分割数とし、これで全長を割りなおして細分の長さを算出する。その長さは指定したminLengthより若干小さくなるが、minLengthをそのまま使ってしまうとうまく均等割りできないのでそうしている。

　なお、closedというオプションがある。これは末尾の点の次の点が存在するかどうかという話である。non-closedがデフォルトだが、この場合最初から最後までのスパンで考える。しかしclosedの場合、最後の点の次の点を最初の点とみなす。なので、closedの場合はpointsに末尾の点を加える。それで計算する。この後の計算で末尾の点が残るようだったら、その時は排除する。

　本番では、まず最初の点を加えたうえで、点を順繰りにフェッチしていく。先ほど算出したproperなlengthごとに、必要ならlerpして点を採取していく。余りを計算し、常に折れ線の長さの和が指定した長さくらいになるようにする。こうして点を取っていく。

　すると末尾の点が入るかどうかが微妙な感じになる。まず、何でもいいからとりあえず末尾を入れてしまう。入れたうえで、近すぎたら弾けばいい。それでうまくいく仕組みである。なお、closedで頭とおしりが同じ点であっても問題ない。どうせ順繰りのlerpで弾かれる。

　最後に、closedであれば末尾をカットする。これでウロボロスにならなくて済む。おわり。

　showDetailはチェック用である。これを使ってどの程度均等か調べている。

quadBezierize（二次ベジエ近似）

　これは与えられた点列に対して、non-closedの場合は頭とおしりの他、中間点の列を作り、最初と最後は直線でつなぎ、それ以外はもともとあった点を二次ベジエのコントロールポイントとして曲線でつなぐ。detailは分割数である。closedの場合は、頭とおしりを含めてすべての中点を用意して、もともとあった点はすべてコントロールポイントとなり、全部二次ベジエでつなげて作るものとする。

式を見ると分かるが3次元にも対応している。もちろんevenlySpacingも3次元でも使える仕様である。

適用

　これらをどう使うかというと、まず最終的に12くらいずつの幅になっているようにする。そのうえで、まず24で均等割りする。それからできた点列に対して二次ベジエ化を実行し、それにより得られる大量の点を12で均等割りして仕上げる。均等割りだけだと折れ線の延長になってしまうし、均等割りしないで二次ベジエ化すると汚くなるのでこうしている。なお、リリースポイントが始点に近いかどうかでclosedか決めている。近い場合にclosedとなるようにしている。

function mouseReleased(){
  if(!isActive) return;
  const closed = (mypoints[0].dist(mypoints[mypoints.length-1]) < 24 ? true : false);
  evenlySpacing(mypoints, {minLength:24,closed, showDetail:true});
  quadBezierize(mypoints, {detail:8, closed});
  evenlySpacing(mypoints, {minLength:12,closed, showDetail:true});
  isActive = false;
  isClosed = closed;
}

おわりに

　雑に引いた線が滑らかになるのは気持ちいいですね。
　ここまでお読みいただいてありがとうございました。

追記

　一応、マウスでも、タッチでも、スタイラスペンでも機能する完全版を置いておきます。ダブルクリックでリセットできます。気のすむまで遊んでいただければと思います。
　point draw Vanilla