Fortranを使ってNまでの素数を求めるプログラムを最速実行する

概要

ネタ投稿です．コンパイル時に計算すれば実行は最速にならざるを得ません．

環境

• Windows 11 64 bit
• gfortran 11.2
• Intel Fortran classic 2021.4.0

Nまでの素数の計算

Nまでの素数の計算は，プログラミングの例題であったり，実行速度の比較であったり，記述力（どれだけ短く書けるか）の比較に使われたりします．

Fortranでも色々な書き方はできますが，実行速度としてはイマイチという評価になっているようです．一方で，他の言語では，コンパイル時に評価される機能を使って高速化をしている例があるので，コンパイル時に色々やってよいのであれば，Fortranでもコンパイル時計算を行うことで高速化できるはずです．

Arjen Markusは，コンパイル時にNまでの素数をparameterとして計算する実装を示し，mecej4によってその修正版が作られました．その実装を下記に示します．

program prime_numbers
    use, intrinsic :: iso_fortran_env
    implicit none

    integer(int32), parameter :: N = 10000
        !! 素数を探索する範囲の上限
    integer(int32), parameter :: rootN = int(sqrt(real(N)))
        !! Nの平方根

    integer(int32) :: i, j
    integer(int32), parameter :: candidates(*) = [2, (i, i=3, N - 1, 2)]
        !! 素数の候補となる整数
        !! 2の倍数は最初から除いておく
    integer(int32), parameter :: multiples(*) = [((i*j, i=j, N/j, 2), j=3, rootN, 2)]
        !! 倍数
        !! 計算する範囲を段階的に縮小
    integer(int32), parameter :: primes(*) = pack(candidates, &
                                                  [(all(candidates(i) /= multiples), &
                                                    i=1, size(candidates))])
        !! multiplesに存在しない値（＝素数）をcandidatesから抜き出し

    print *, primes
end program prime_numbers

まず，candidates(*) = [2, (i, i=3, N - 1, 2)]において，2と3からN-1までの奇数を作成します．

次のmultiples(*) = [((i*j, i=j, N/j, 2), j=3, rootN, 2)]では，Nまでの倍数を計算します．反復がちょっとわかりにくいのですが，iとjの範囲を絵にしてみると，かなり理解しやすくなります．下の図中の緑のセルが，N=100として実行したときのiとjの取り得る値です．

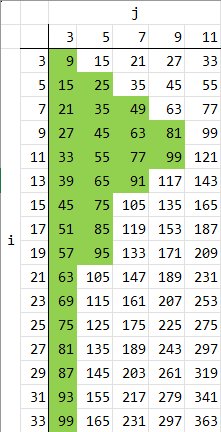
最後に，packを用いて，candidatesからmultiplesに存在しない値（＝素数）を抜き出します．

この処理はすべてコンパイル時に行われるため，作成された実行ファイルを実行すると，print *, primesによって計算済みの素数が表示されます．計算は一切行われないので，最速で実行されます．もちろん，Nが大きくなるとコンパイルに時間はかかりますが，プログラムの実行速度の比較においてコンパイル時間は勘定されないのが通例ですから，何の問題もありません．

Fortranに組み込みの集合演算があれば，multiples中の重複の解消と，pack関数中のループを削除できそうなのですが，その未来は訪れないような気がします．

まとめ

コンパイル時計算は色々便利に使えそうな気がします．