Go to Qiita Advent Calendar 2024 Top
LoginSignup
31
26

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

数値計算Advent Calendar 2018

Day 3
@implicit_none

とても簡単な4段4次のRunge-Kutta法について

Last updated at Posted at 2018-12-02

これは数値計算 Advent Calendar 2018 3日目の記事です．

Twitterでのブームは去ってしまいましたが，実装が簡単な4段4次のRunge-Kutta法について紹介します．

古典的Runge-Kutta法

時間変化する物理現象を数値的に予測する際，物理量の初期値を与えてその時間変化を追跡します．Runge-Kutta法はそのような時間積分を行う数値計算法の一つです1．

ここでいう古典的なRunge-Kutta法は，教科書に載っているような4段4次の方法です．

\begin{eqnarray}
    f^{(2)} &=& f^n + \frac{\Delta }{2} F(t,f)\\
    f^{(3)} &=& f^n + \frac{\Delta t}{2} F(t+\Delta t/2,f^{(2)})\\
    f^{(4)} &=& f^n + \Delta t   F(t+\Delta t/2,f^{(3)})\\
    f^{n+1} &=& f^n+\Delta t \frac{ F(t,f^n)+2F(t+\Delta t/2,f^{(2)})+2F(t+\Delta t/2,f^{(3)})+F(t+\Delta t,f^{(4)})}{6}
\end{eqnarray}

プログラムで書くと，このような感じでしょうか．

                         df1 = d_f_dt(t       ,f )
    f2 = f + dt/2d0*df1; df2 = d_f_dt(t+dt/2d0,f2)
    f3 = f + dt/2d0*df2; df3 = d_f_dt(t+dt/2d0,f3)
    f4 = f + dt    *df3; df4 = d_f_dt(t+dt    ,f4)
    f  = f + dt*(df1+2d0*df2+2d0*df3+df4)/6d0

f?が各サブステップでの物理量$f^{(m)}$，df?は当該サブステップでの時間導関数です．d_f_dt()はfの時間微分値を返す関数です．
時間微分値を返す関数の引数に計算式を書かず，わざわざサブステップでの物理量を用意しているのは，スタックあふれへの対策です．$f$がスカラーでない場合，fは配列になります．配列の演算を引数として関数に渡した場合，演算結果を格納する配列が暗黙的に割り付けられるのですが，そのサイズが大きいとスタックオーバーフローを引き起こします．

非常に強力な時間積分法ですが，我々の分野では古典的Runge-Kutta法はほとんど使われません．色々と理由はありますが，一つの大きな理由はメモリの使用量です．古典的Runge-Kutta法は，単純な実装だとメモリ使用量が多いのです．上式において，$F(t,f)$は時間微分$\partial f/\partial t$に相当しますが，その値とサブステップでの値$f^{(m)}$（中間変数）を保持しなければなりません．物理量を保持する配列の要素数をNとしたとき，一つの物理量に対して，物理量とその微分値（計2N）以外に7N分の中間変数が必要です．

下記のような省メモリ実装もできますが，どうしても2N分の中間変数は必要ですし，計算過程で二つの変数を更新することになります．

    fn = f
    df = d_f_dt(t       ,f   ); fmid = fn + dt*df/2d0; f = f + dt*df/6d0
    df = d_f_dt(t+dt/2d0,fmid); fmid = fn + dt*df/2d0; f = f + dt*df/3d0
    df = d_f_dt(t+dt/2d0,fmid); fmid = fn + dt*df    ; f = f + dt*df/3d0
    df = d_f_dt(t+dt    ,fmid)                       ; f = f + dt*df/6d0

簡単な問題ならまだ管理できますが，複数の物理量（質量，運動量，運動エネルギ等）を同時に時間積分するときは，非常に厄介です．

古典的Runge-Kutta法と同じく4段4次で，かつ実装が簡単な方法を示します．

Jameson-BakerのRunge-Kutta法

Jameson-BakerのRunge-Kutta法は，Runge-Kutta法の変種の一つであり，名前の通りJamesonとBakerの論文2の中で言及されています．

\begin{eqnarray}
    f^{(1)} &=& f^n + \alpha_1\Delta t F(t+\beta_1\Delta t,f^n)\\
    f^{(2)} &=& f^n + \alpha_2\Delta t F(t+\beta_2\Delta t,f^{(1)})\\
    f^{(3)} &=& f^n + \alpha_3\Delta t F(t+\beta_3\Delta t,f^{(2)})\\
    f^{n+1} &=& f^n + \alpha_4\Delta t F(t+\beta_4\Delta t,f^{(3)})
\end{eqnarray}

係数$\alpha, \beta$にはそれぞれ以下の値を採用します．

\begin{pmatrix}
    \alpha_1 \\
    \alpha_2 \\
    \alpha_3 \\
    \alpha_4
\end{pmatrix}
=
\begin{pmatrix}
    \frac{1}{4} \\
    \frac{1}{3} \\
    \frac{1}{2} \\
    1
\end{pmatrix},\quad
\begin{pmatrix}
    \beta_1 \\
    \beta_2 \\
    \beta_3 \\
    \beta_4 
\end{pmatrix}
=
\begin{pmatrix}
    \frac{1}{3} \\
    \frac{1}{2} \\
    \frac{1}{2} \\
    \frac{1}{2}
\end{pmatrix}

各サブステップで参照する時間$\beta$については，論文内では言及されていません．試行錯誤的に試した結果，この組み合わせを用いると最も誤差が小さくなりました．3

プログラムでは次のように書けます．

    fn = f
    f = fn + dt/4d0*d_f_dt(t+dt/3d0,f)
    f = fn + dt/3d0*d_f_dt(t+dt/2d0,f)
    f = fn + dt/2d0*d_f_dt(t+dt/2d0,f)
    f = fn + dt    *d_f_dt(t+dt/2d0,f)

あるいは

    integer :: s
    real(8),parameter :: subtime(4) = [1d0/2d0, 1d0/2d0, 1d0/2d0, 1d0/3d0] 
    fn = f
    do s = 4, 1, -1
        f = fn + dt/s*d_f_dt(t+subtime(s)*dt,f)
    end do

各サブステップの値を個別に保持する必要は無く，fn（$f^n$の値）を保持しておけば，fを順次上書きしていくことができます．一つの物理量に対して，物理量とその微分値（計2N）以外に必要となる中間変数は1Nのみです．

本記事で取り上げる問題では無事に4次精度が出ていますが，解析的に局所誤差が$O(\Delta t^5)$であることは示されていません．JamesonとBakerは，線形方程式に対しては古典的なRunge-Kutta法と同じである2と述べているだけです．

テスト問題1

支配方程式と厳密解

非常に簡単な，時間に関する常微分方程式

\frac{d f}{dt} = F(t,f)\\
F(t,f) = -tf

を時間積分します．上式の解は

f_{ex} = f_0 e^{-t^2/2}

です．$f_0$は$f$の初期値で，今回は$1$としました．そのときの$f$の分布を下図に示します．

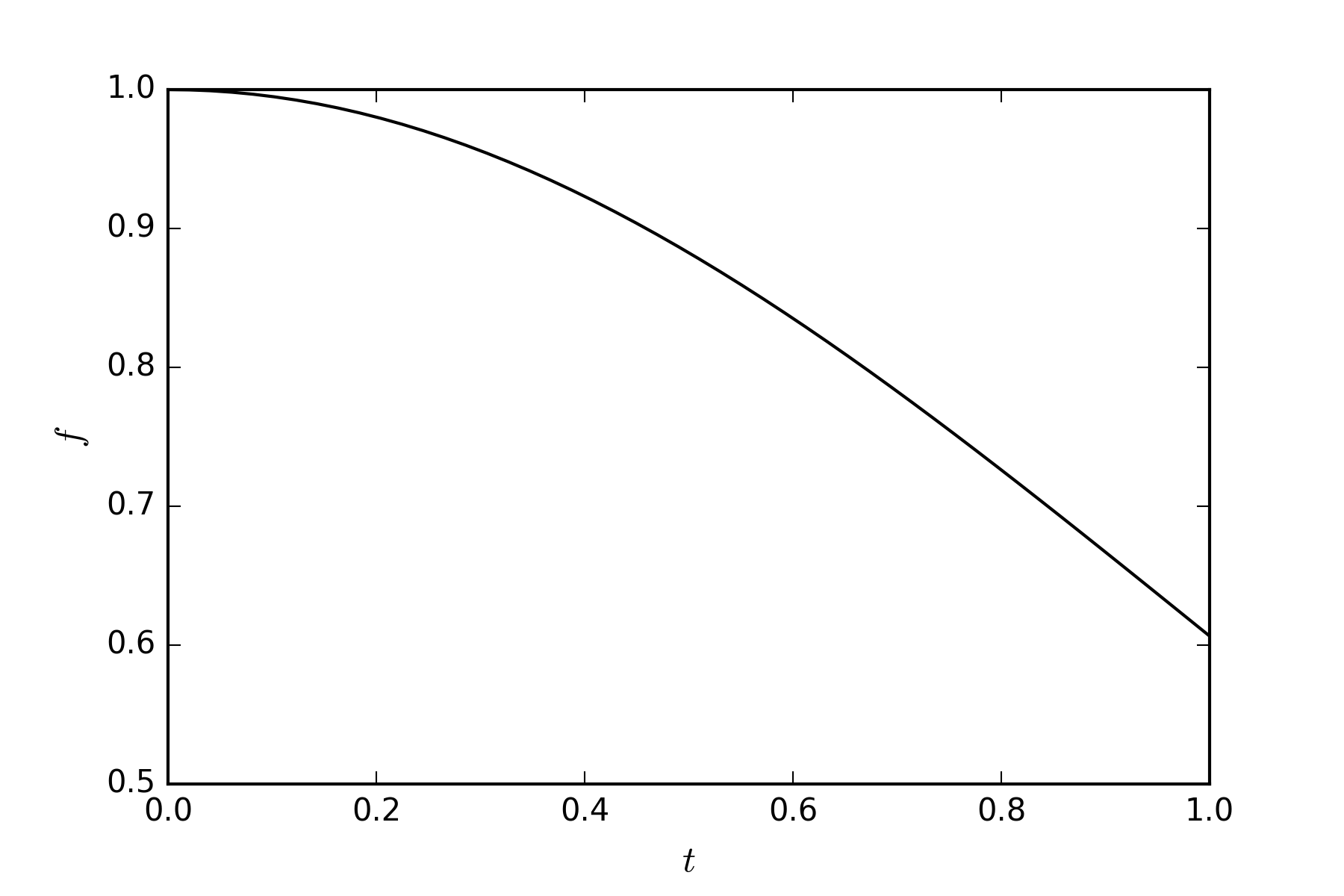
計算時間間隔を$10^{-6}$から$10^0$まで変化させて，$t＝0$から$T_{\mathrm{end}}(=1)$まで計算を行い，$T_{\mathrm{end}}$における相対誤差を次の式で評価しました．

\varepsilon = \frac{|f-f_{ex}|}{f_{ex}}

計算にはすべて倍精度実数（real(8)）を用いました．

計算結果

結果を下図に示します．$\mathrm{JB-RK}$がJameson-BakerのRunge-Kutta法による計算結果で，比較のために古典的Runge-Kutta法による計算結果（$\mathrm{RK4}$）も併記されています．

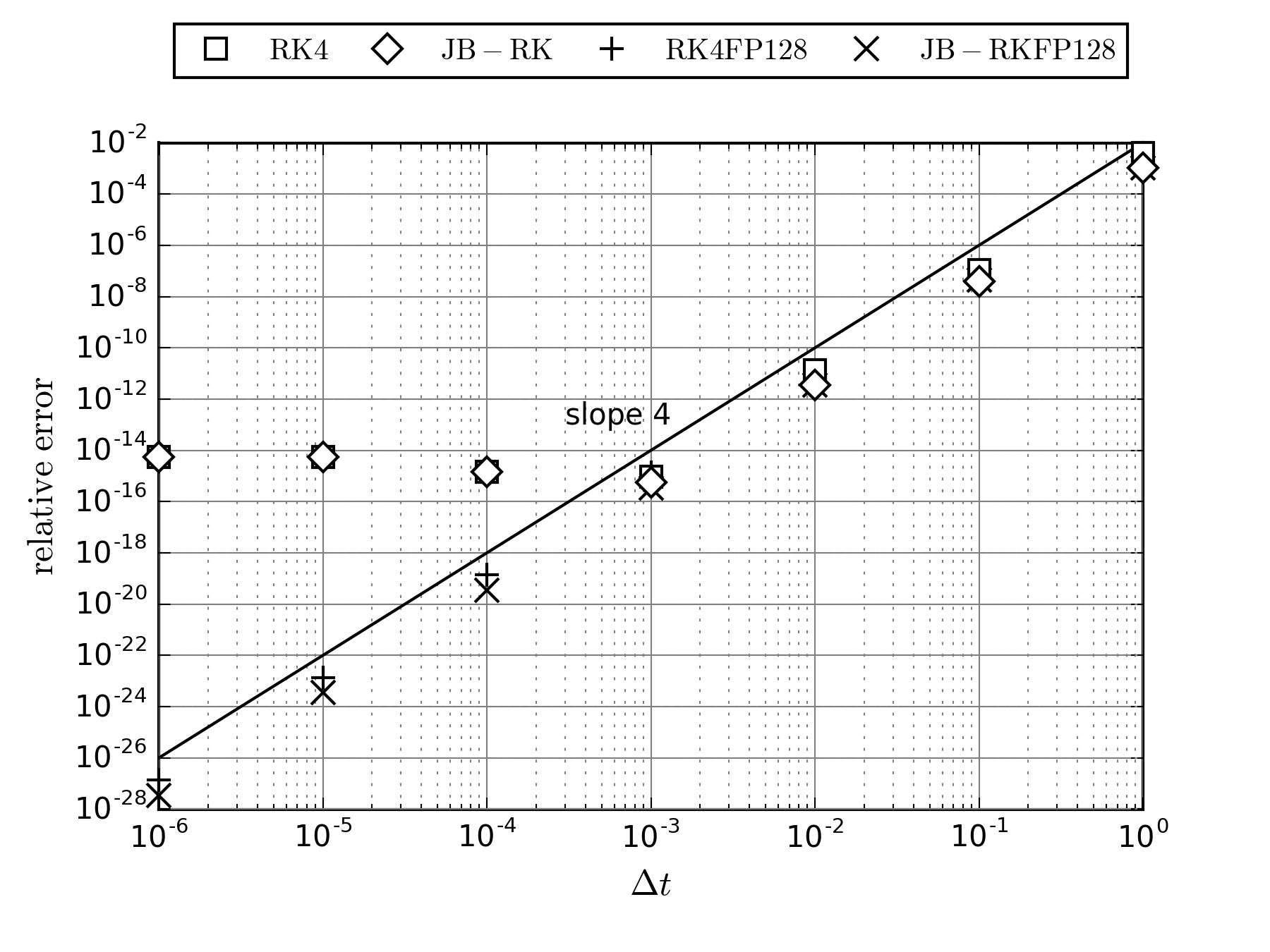
Jameson-BakerのRunge-Kutta法の方が若干（といってもおよそ一桁）誤差が小さいようです．古典的Runge-Kutta法とJameson-BakerのRunge-Kutta法共に傾き4で誤差が減少します．つまり，大域誤差が$\Delta t$の4乗に比例して減少しているので，4次精度を達成できていることがわかります．

誤差は$10^{-15}$まで単調に減少した後，増加に転じます．打ち切り誤差が十分小さくなり，計算過程で丸め誤差が蓄積するためです．

4倍精度実数（real(16)）で実行すると，$\Delta t$を$10^{−3}$より小さくしても，誤差は増えることなく単調に減少しています．$\Delta t\ge 10^{−3}$では倍精度実数で計算した結果と一致します．

テスト問題2：1次元移流方程式

支配方程式および厳密解

1次元移流方程式は次式で表されます．

\frac{\partial f}{\partial t} + c\frac{\partial f}{\partial x} = 0

$c$は移流速度で，簡単のために$c=1$としました．

移流方程式の厳密解は次式で表すことができます．

 f(t,x)=f(t,x-c\Delta t)

$f$はその形を保ったまま速度$|c|$で$c$の符号の方向へ移動することを意味しています．この性質を利用すると，移流方程式の計算結果の評価が簡単になります．計算領域の両端に周期境界条件を課すことで，片方の境界から流出した$f$がもう片方の境界から流入するので，いくらでも長い時間計算できます．また，計算時間をうまく設定してやると，$f$が計算領域を何周かして初期値と同じ場所に帰ってくるので，誤差評価もしやすくなります．

移流方程式を変形すると，次のようになります．

\frac{d f}{dt} = F(f)\\
F(f) = - c\frac{\partial f}{\partial x}

形式上，時間導関数$F$が位置$x$のみの関数として表されています.これは$F$を解析的ではなく数値的に計算することに起因していて，計算に用いるfに時間の影響が暗に含まれるからです．したがって，積分の過程で$\beta$を使うことはありません．

Jameson-BakerのRunge-Kutta法を適用すると，時間積分は

    fn = f
    do s = 4, 1, -1
        call computeGradient(d_f_dx, f, dx)
        f(:) = fn(:) + dt/s* -c*d_f_dx(:)
    end do

と計算することができます．サブルーチンcomputeGradientにおいて，$f$の空間微分$\partial f/\partial x$を計算します．

空間微分の計算

1階空間微分は8次精度の陽的差分で計算します．

\frac{\partial f}{\partial x} = \frac{4}{5}\frac{f_{i+1}-f_{i-1}}{\Delta x}-\frac{1}{5}\frac{f_{i+2}-f_{i-2}}{\Delta x}+\frac{4}{105}\frac{f_{i+3}-f_{i-3}}{\Delta x}-\frac{1}{280}\frac{f_{i+4}-f_{i-4}}{\Delta x}

計算領域の両端には周期境界条件を課すので，i+1やi-1などが配列外参照する場合には，modulo()を使って参照位置を修正しました．

    ip4 = modulo((i+4)-1, N) + 1
    ip3 = modulo((i+3)-1, N) + 1
    ip2 = modulo((i+2)-1, N) + 1
    ip1 = modulo((i+1)-1, N) + 1
    im1 = modulo((i-1)-1, N) + 1
    im2 = modulo((i-2)-1, N) + 1
    im3 = modulo((i-3)-1, N) + 1
    im4 = modulo((i-4)-1, N) + 1
    d_f_dx(i) =  4d0/  5d0*(f(ip1)-f(im1))/dx&
               +-1d0/  5d0*(f(ip2)-f(im2))/dx&
               + 4d0/105d0*(f(ip3)-f(im3))/dx&
               +-1d0/280d0*(f(ip4)-f(im4))/dx

初期条件および計算条件

$f$の初期値は次の式で与えました．

f_0 = \sin \left( \frac{2\pi x}{L_w} \right) \exp\left(-\ln 2 \left[\frac{2\pi x}{h}\right]^2\right)

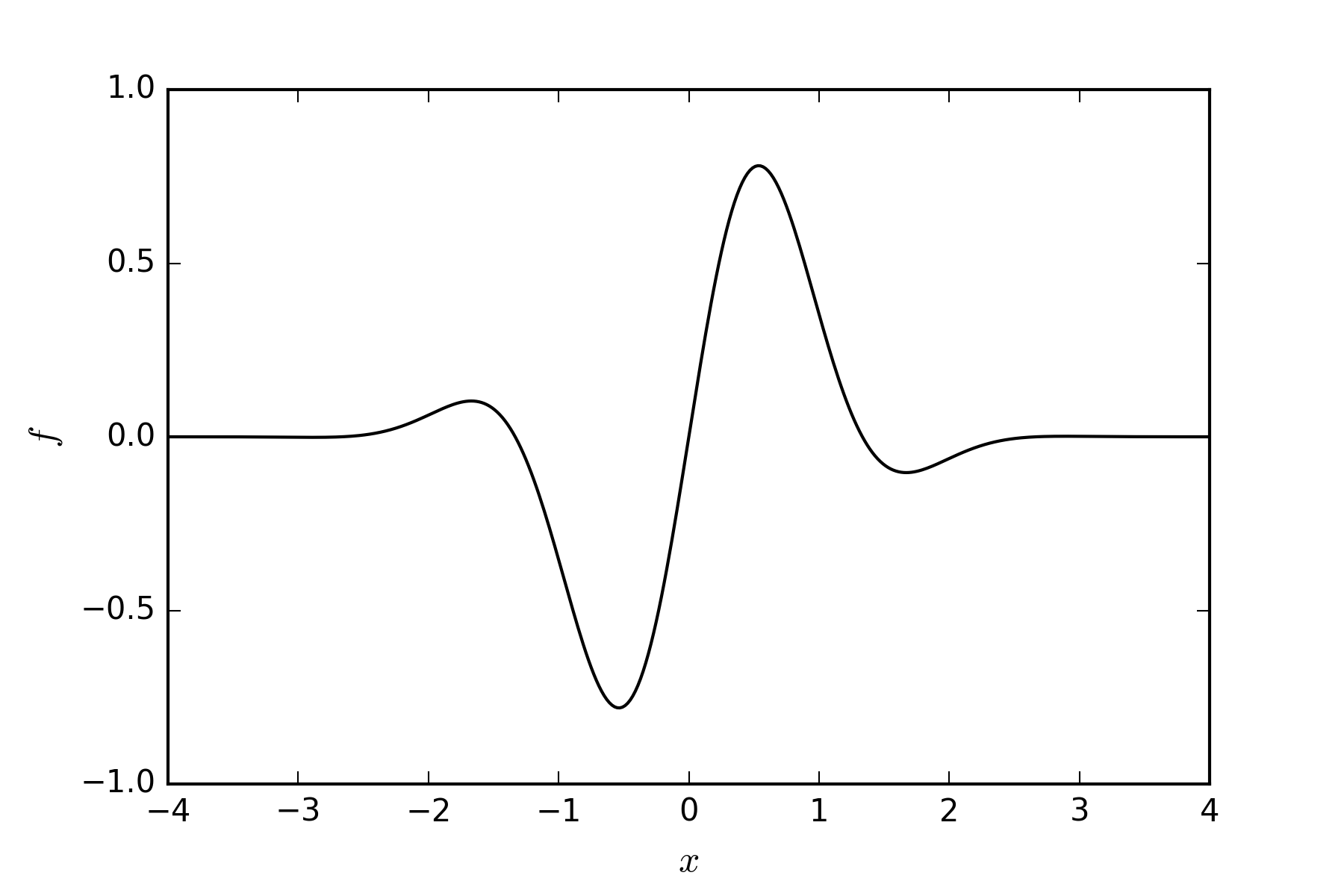
$L_w$は波の波長，$h$はGauss分布の半値幅です．計算領域の長さを$L_x$として，ほどよい結果が得られるように試行錯誤的にそれぞれ$L_w=2L_x/30, h=2\pi L_x/40$としました．この条件で定められる波の形状を下図に示します．

計算領域を$−20\le x \le 20$，つまり$L_x=40$としました．この領域に，等間隔（$\Delta x$間隔）に800点のサンプリング点を置いて（$N=800$），その点での$f$の変化を計算しました．計算は$t=0$から$T_{\mathrm{end}}(=80)$まで行いました．この条件で計算すると，波が形を維持しながら計算領域を2周し，初期位置に戻ってきます．$T_{\mathrm{end}}$の$f$と初期値の絶対誤差の平均値を評価の指標としました．

\varepsilon = \frac{1}{N}\sum{\left| f-f_0 \right|}

計算時間間隔は，次式で定義されるCourant数を$0.04$, $0.05$, $0.08$, $0.1$, $0.16$, $0.2$, $0.25$, $0.4$, $0.5$, $0.8$, $1$として，そこから$\Delta t$を得ました．

\Delta t = \mathrm{CFL}\frac{\Delta x}{c}

これらの数字を選んだ理由は，計算終了時間$T_{\mathrm{end}}(=80)$と計算時間間隔$\Delta t$から計算回数を決める際に，$T_{\mathrm{end}}/\Delta t$が割り切れるようにするためです．

計算結果

計算結果を下図に示します．$\mathrm{JB-RK(N=800)}$がJameson-BakerのRunge-Kutta法，$\mathrm{RK4(N=800)}$が古典的Runge-Kutta法による結果です．両者の結果は完全に一致しており，これは計算結果の数値を見ても，小数点以下6位程度までは一致します．

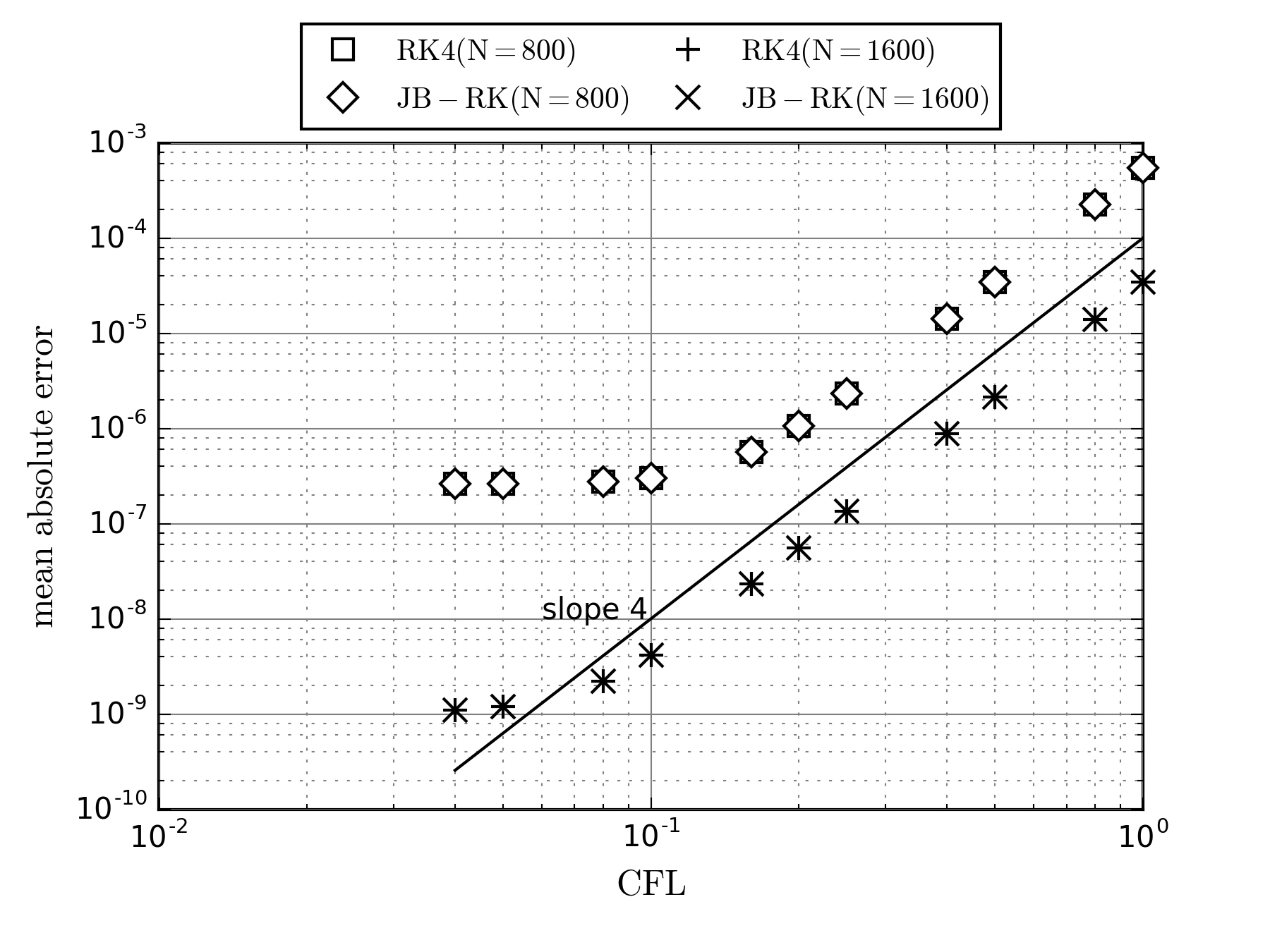
横軸は$\Delta t$ではなくCourant数としています．

テスト問題1と同様に，両者とも傾き4で誤差が減少します．テスト問題1では，サブステップで参照する時間を適当に調整することでJameson-BakerのRunge-Kutta法の誤差を小さくすることができましたが，移流方程式に対してはそういった調整はできません．

一方で，Courant数が$1$から$0.2$までは，誤差は単調に減少しますが，$0.1$以下では一定値（$3\times 10^{−6}$程度）を取ります．この誤差の停滞は，時間積分に伴う誤差や丸め誤差が主要因ではなく，空間差分の打切り誤差に起因します．空間微分には8次精度の陽的差分を用いていますが，サンプリング点数$N$が$800$では少なすぎるということでしょう．$N$を倍の1600に増やすと，$N=800$の時よりも誤差が小さくなり，かつCourant数$0.1$以下でも単調に減り続けます．しかしCourant数$0.05$，誤差$10^{−9}$程度で停滞し始めます．8次精度の陽的差分は，誤差が$\Delta x^8$に比例して減少していくので，$\Delta x$が半分になった場合には，2桁ちょっと誤差が減る計算です．Courant数$0.04$での誤差を$N=800$と$N=1600$で比較すると，この見積もりどおりであることがわかります．

本記事の主目的は時間積分法の話ですが，適用する問題によっては時間積分法以外にも気を遣うべきであることがわかります．10次精度のコンパクト差分を使った結果を当サークルの同人誌4に掲載しています．

まとめ

とても簡単な4段4次精度のRunge-Kutta法（Jameson-BakerのRunge-Kutta法）を紹介しました．今回のテスト問題2個に対しては，非常に簡単な実装で4次精度が達成できました．しかし，解析的に証明はされていませんし，安定条件も古典的Runge-Kutta法と比較してどうかはわかりません．非線形問題でも4次精度が出るかどうかも不明です．気になる人はぜひ色々と調べてみてください．

  1. ある物理量がわかっていて，ある軸に沿ってその1階微分が計算できるときに，物理量を軸方向に補外する方法と見なすこともできます． ↩

  2. Jameson, A., Baker, T.J., "Solution of the Euler equations for complex configurations," AIAA Paper 83-1929. ↩ ↩2

  3. テスト問題1で調査した結果です．問題依存だと思いますが，$\beta_1$は適当でも形式的な精度には影響しません．$\beta_2\neq 1/2$の時は3次精度，$\beta_3\neq 1/2$の時は2次精度，$\beta_4\neq 1/2$の時は1次精度に落ちます． ↩

  4. 暗黙の型宣言編著，空力音の直接数値計算を支える技術，2018． ↩

31
26
4

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
31
26

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?